Запуск сообщества разработчиков печатных плат / Хабр

С прошлой самопиар-публикации прошло почти 2 года, была проделана большая работа, о которой снова хочется рассказать.

Руководство

по проектированию с того момента пережило 4 релиза, появилось несколько напечатанных экземпляров, и сейчас оно мне уже очень нравится по содержанию, хотя это точно не финальная версия и всегда есть, куда становиться лучше. Но здесь не о нём, здесь о новом проекте — платформе для разработчиков печатных плат.

После релиза книги я был нацелен на разработку удобных средств расчётов для разработчиков. Теперь эта идея выросла в более интересный проект и реализована в виде платформы для разработчиков печатных плат

SamsPcbLab

.

Это сейчас она реализована, а три месяца назад ничего ещё не было, кроме эскизов страниц на бумаге. Первым делом узнал, сколько стоит web-разработка той функциональности, которая мне нужна. Сразу же после этого стал думать, смогу ли сделать самостоятельно.

Смог, за одно в процессе узнал про CSS и PHP, о своём опыте разработки я рассказал в отдельной публикации. Здесь же о том, что есть на данный момент.

Лирическое отступление. Сразу скажу, что сообщество закрытое с платной подпиской. Хочется сделать удобную функциональную платформу с уникальной базой знаний, и для развития проекта нужно топливо. Но я не хочу рекламы на сайте, не хочу спам в комментариях. Цель в создании экспертного сообщества с атмосферой единого коллектива и общими ценностями:

1. Уважение, в широком смысле. И к другим, и к себе, и к работе своей и других.
2. Отсутствие конечной точки, остановки в познании. Жадность при накоплении знаний, но щедрость при их передаче. Здесь ещё есть момент честности – признаться себе, что что-то не понимаешь, не знаешь. И искать ответы, задавать вопросы, не оставлять пробелов в понимании за спиной.
3. Техническая эстетика разрабатываемых изделий. То, что красиво выглядит, с большей вероятность хорошо работает.
   Это не обязательно так. Но тут опять же про уважение, к своей работе, к производству, к нюансам, к симметрии и золотому сечению.
4. Хороший юмор, дополненный бонусом самоиронией.

Ценности эти выше материальных, поэтому за их несоблюдение (прежде всего первой, конечно) я буду блокировать учётную запись с возвратом подписки. Мне бы хотелось, чтобы в сообществе была максимально продуктивная атмосфера и возникали совместные проекты.

И пользуясь случаем, передаю привет и выражаю благодарность всем читателям, которые поддерживали проект. Сделал для вас бесплатную годовую подписку, о чём делал рассылку. Для остальных есть ознакомительная подписка на неделю.

Калькуляторы

В таблицах представлен перечень реализованных на данный момент калькуляторов. Это отправная точка. Концепция в том, что сообщество определяет набор вычислительных средств с помощью голосования в разделе «Обратная связь». Планируются следующие калькуляторы: тепловые расчёты, расчёт индуктивности катушек, в том числе планарных, расчёт трансформаторов, в том числе планарных, расчёт RLC-фильтров, резонанс конденсаторов по питанию, различные простые специфические расчёты типа резистора для светодиода или резистивного делителя.

Для всех калькуляторов выбрана модель, которая даёт лучшие результаты на эталонных данных. Известные модели и расчётные формулы дорабатываются – например, для ассиметричной полосковой линии добавлена возможность задать разные диэлектрики, для формул максимального тока добавлены частотные зависимости с учётом скин-эффекта и т.д. Выбор модели и теоретическая основа каждого калькулятора будут описаны в базе знаний, а также освещаться в блоге на платформе.

Таблица 1. Калькуляторы индуктивности (Приложение А руководства).

Таблица 2. Калькуляторы волнового сопротивления (Приложение Б руководства).

Таблица 3. Максимальный ток проводника (Глава 2 руководства).

Таблица 4. Перекрёстные помехи (Глава 3 руководства).

Таблица 5. Тепловой расчёт.

База знаний

Изначально просто разместил книгу на платформе в pdf-формате, но это не давало возможности делать ссылки на книгу. Оптимальным решением стало создание базы знаний, где будут не только разделы книги, но о теоретическая основа для каждого калькулятора, FAQ, а также собрана и систематизирована вся полезная информация, которая будет появляться в блоге сообщества.

Блог сообщества

Площадка для обмена знаниями внутри сообщества. Любой подписчик (кроме ознакомительной подписки) может опубликовать запись, выбрав соответствующую категорию публикаций:

• Вопросы по разработке.
• Мой проект. Ориентировочное направление потока – ведение блога разработки, привлечение разработчиков в команду, совместный поиск решения.
• Новости. Любые интересная и полезная отраслевая информация – анонсы вебинаров, новая элементная база и т.п.
• Полезное. Ссылки, приёмы и средства разработки, опыт разработки – как успешный, так и собственные ошибки, настройки САПР и всё, что, на Ваш взгляд, повышает эффективность и качество разработки.
• Работа | подработка. Ваше резюме, рекрутинг специалистов.
• Полезное. То, чем хочется поделиться, но что не попадает в тематику других рубрик.

Первое время, до выработки стандарта качества сообщества («Хабр» тут является хорошим ориентиром), я буду модерировать публикации.

В блоге буду освещать работу над калькуляторам, также хочу сделать рубрики разные. Например, планирую сделать «100 дней с Богатиным», где каждый день будем разбирать одну из его рекомендации по проектированию печатных плат.

Личная переписка

Нашёл один плагин для WordPress с такой функциональностью, интерфейс визуально немного облагородил. Считаю, что нужна возможность для создании личных контактов, вообще буду рад, если платформа поспособствует продуктивному сотрудничеству.

---

На этом пока всё. Я приглашаю в

сообщество

всех, кому близки указанные выше ценности, всех, кому интересна моя работа и кто готов поддержать дальнейшее развитие проекта. В сообществе буду рад видеть как начинающих разработчиков, так и экспертов, было бы просто прекрасно, если бы сообщество поспособствовало выстраиванию передачи опыта – это то, что было потеряно в отрасли из-за просадки 90-ых годов. Но я убеждён, что в отрасли много опытных специалистов, которым есть, чем поделиться.

Всем успехов!

Аттенюатор для гитарных ламповых комбиков

---

&nbsp &nbsp &nbsp Автор: Михаил Южаков
&nbsp &nbsp &nbsp Дата публикации: 07 марта 2018 г.

---

В статье приведены различные варианты построения аттенюаторов для ламповых комбоусилителей: простые и сложные, удачные и неудачные.

Став в своё время счастливым обладателем лампового комбика, я одновременно озадачился тем, чтобы собрать или приобрести ламповый аттенюатор: более или менее «вкусный» звук ламповый усилитель выдаёт при достаточно большом уровне громкости (даже на чистом звуке). Например, мой скромный Yerasov GTA-15 «требовал» уровня громкости минимум 3 из 10, однако в масштабах моей весьма небольшой комнаты играть на таком уровне было уже некомфортно.

В силу этого я опробовал несколько различных схем аттенюаторов для комбиков и решил систематизировать опыт их построения и использования в этой статье.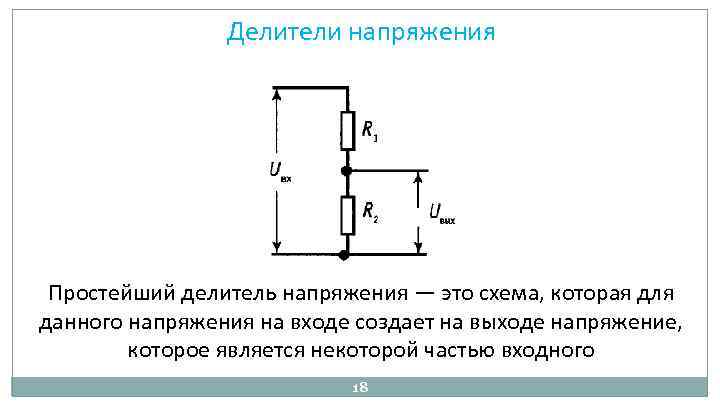

1. Простейший гасящий резистор (неудачный вариант)

Ламповый усилитель имеет токовый выход — напряжение на выходе определяется импедансом нагрузки. В идеальном варианте:

Uвых = Iвых * Zн, где Uвых – напряжение на выходе, Iвых – выходной ток усилительного прибора, Zн – импеданс нагрузки.

Повышая импеданс нагрузки последовательным включением резистора, повышаем выходное напряжение, что может привести к выходу оконечного каскада из строя; кроме того, ламповый комбоусилитель рассчитывается исходя из конкретного значения сопротивления нагрузки и при изменении сопротивления нагрузки выходит из расчетного режима. В моём случае гитарный комбик просто захрипел, что говорит о появлении динамических искажений (ограничения сигнала).

Вывод: ламповый аттенюатор по входу должен имитировать импеданс динамика – хотя бы резистивную часть.

2. Резистивные делители

Простейший резистивный делитель, обеспечивающий фиксированное ослабление -6дБ:

Такого ослабления оказалось недостаточно. Кроме того, даже при таком небольшом ослаблении гитарный звук кажется более плоским, «картонным».

Другой вариант, П-образный аттенюатор:

В Сети есть большое количество онлайн-калькуляторов под эти схемы для расчета номиналов под требуемое ослабление.

Ступенчатый аттенюатор. Простейший пример:

Аттенюатор «Yerasov muffler». Собран фактически по схеме резистивного делителя.

Muffler-15
Muffler-30

У всех этих схем есть недостаток: они не совсем повторяют частотную характеристику усилителя. Для лампового усилителя характерна зависимость АЧХ от импеданса динамика: в соответствии с формулой п.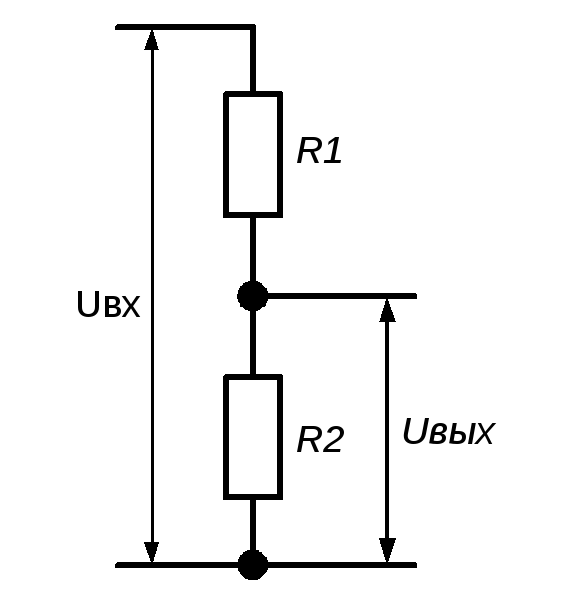 1, напряжение на выходе зависит от комплексного сопротивления нагрузки. Резистивный делитель же «отсекает» импеданс динамика от выхода усилителя. Вот поэтому у меня и гитарный звук был «картонным». Применение таких аттенюаторов может быть оправдано в некоторых случаях – например, у Ерасова в аннотации написано, что этот аттенюатор предназначен для работы в режиме перегруза.

3. Схема В.Кемпфа: гитарный аттенюатор с имитацией реактивного импеданса динамика

В этой замечательной схеме (первоисточник) присутствуют две параллельных ветви. Первая ветвь имитирует импеданс динамика, вторая ветвь представляет собственно резистивный аттенюатор. Причем работа первой и второй ветви мало зависит друг от другая (сопротивление второй ветви большего порядка).

Дело за малым — осталось привести «технологические» параметры, в частности намоточные данные катушек индуктивности и/или их тип. Привожу свою схему по мотивам. Схема рассчитана на работу с ламповым усилителем до 50Вт; опробована на усилителе Yerasov GTA-15.

В качестве второй ветви аттенюатора здесь реализован многоступенчатый резистивный делитель; резистор R9, включенный последовательно с выходом делителя, помог устранить «картонный» звук гитары, который в этой схеме проявлялся только на самых сильных уровнях ослабления.

Схема, обведённая пунктиром, это опция – спиксим для записи в линию. Её можно не собирать. Повторяет АЧХ динамика, ослабляя сигнал с помощью делителя.

Конструктивные параметры катушек индуктивности

Катушки аттенюатора L1, L2 выполнены без сердечника. Это важно, так как ферриты имеют нелинейную характий вид аттенюатора для комбика» src= «/images/guitar/resize/?z=500&file=/files/make/attenuator-dlja-gitarnogo-kombika/08.jpg» title=»Внешний вид аттенюатора для комбика» />

Эксплуатирую этот аттенюатор 2-3 года, впечатления исключительно положительные.

Расчет смещения (биполярные транзисторы)

Добавлено 23 октября 2017 в 00:45

Сохранить или поделиться

Хотя транзисторные коммутационные схемы работают без смещения, для аналоговых схем работать без смещения – это необычно. Одним из немногих примеров является радиоприемник на одном транзисторе в разделе «Радиочастотные схемы» главы 9 с усиливающим АМ (амплитудная модуляция) детектором. Обратите внимание на отсутствие резистора смещения базы в этой схеме. В этом разделе мы рассмотрим несколько базовых схем смещения, которые могут устанавливать выбранное значение тока эмиттера I_Э. Учитывая величину тока эмиттера I_Э, которую необходимо получить, какие потребуются номиналы резисторов смещения, R_Б, R_Э и т.д.

Схема смещения с фиксированным током базы

В простейшей схеме смещения применяется резистор смещения базы между базой и батареей базы V_смещ. Использовать существующий источник V_пит, вместо нового источника смещения, – очень удобно. Пример данной схемы смещения показан в каскаде аудиоусилителя в детекторном приемнике в разделе «Радиочастотные схемы» главы 9. Обратите внимание на резистор между базой и клеммой батареи. Подобная схема показана на рисунке ниже.

Напишите уравнение закона напряжений Кирхгофа для контура, включающего в себя батарею, R_Б и падение напряжения V_БЭ на переходе транзистора, на рисунке ниже. Обратите внимание, что мы используем обозначение V_смещ, хотя на самом деле это V_пит. Если коэффициент β велик, мы можем сделать приближение, что I_К = I_Э. Для кремниевых транзисторов V_БЭ ≅ 0.7 В.

Схема смещения с фиксированным током базы

\[V_{смещ} — I_Б R_Б — V_{БЭ} = 0\]

\[V_{смещ} — V_{БЭ} = I_Б R_Б\]

\[I_Б = { V_{смещ} — V_{БЭ} \over R_Б }\]

\[I_Э = (\beta + 1)I_Б \approx \beta I_Б\]

\[I_Э = { V_{смещ} — V_{БЭ} \over R_Б / \beta }\]

Коэффициент β малосигнальных транзисторов, как правило, лежит в диапазоне 100–300. Предположим у нас есть транзистор β=100, какое номинал резистора смещения базы потребуется, чтобы достичь тока эмиттера 1 мА?

Решение уравнения I_Э для определения R_Б и подстановка значений β, V_смещ, V_БЭ и I_Э дадут результат 930 кОм. Ближайший стандартный номинал равен 910 кОм.

\(\beta = 100 \qquad V_{смещ} = 10 В \qquad I_К \approx I_Э = 1 мА \)

\[R_Б = { V_{смещ} — V_{БЭ} \over I_Э / \beta } = { 10 — 0,7 \over 1 мА / 100 } = 930 кОм \]

Чему будет равен ток эмиттера при резисторе 910 кОм? Что случится с током эмиттера, если мы заменим транзистор на случайный с β=300?

\(\beta = 100 \qquad V_{смещ} = 10 В \qquad R_Б = 910 кОм \qquad V_{БЭ} = 0,7 В\)

\[I_Э = { V_{смещ} — V_{БЭ} \over R_Б / \beta } = { 10 — 0,7 \over 910 кОм / 100 } = 1,02 мА \]

\(\beta = 300 \)

\[I_Э = { 10 — 0,7 \over 910 кОм / 300 } = 3,07 мА \]

При использовании резистора стандартного номинала 910 кОм ток эмиттера изменится незначительно. Однако при изменении β со 100 до 300 ток эмиттера утроится. Это неприемлемо для усилителя мощности, если мы ожидаем, что напряжение на коллекторе будет изменяться от почти V_пит до почти земли. Тем не менее, для сигналов низкого уровня от микровольт до примерно вольта точка смещения может быть отцентрирована для β, равного квадратному корню из (100·300), что равно 173. Точка смещения будет по-прежнему дрейфовать в значительном диапазоне. Однако сигналы низкого уровня не будут обрезаны.

Схема смещения с фиксированным током базы по своей природе не походит для больших токов эмиттера, которые используются в усилителях мощности. Ток эмиттера в схеме смещения с фиксированным током базы не стабилен по температуре. Температурный уход – это результат большого тока эмиттера, который вызывает повышение температуры, которое вызывает увеличение тока эмиттера, что еще больше повысит температуру.

Схема автоматического смещения (с обратной связью с коллектором)

Изменения смещения из-за температуры и коэффициента бета могут быть уменьшены путем перемещения вывода резистора смещения с источника напряжения V_смещ на коллектор транзистора, как показано на рисунке ниже. Если ток эмиттера будет увеличиваться, увеличится падение напряжения на R_К, что уменьшит напряжение V_К, что уменьшит I_Б, подаваемый обратно на базу. Это в свою очередь уменьшит ток эмиттера, корректируя первоначальное увеличение.

Напишем уравнение закона напряжений Кирхгофа для контура, включающего в себя батарею, R_К, R_Б и падение напряжения V_БЭ. Заменим I_К≅I_Э и I_Б≅I_Э/β. Решение для I_Э дает формулу I_Э для схемы автоматического смещения при обратной связи с коллектором. Решение для R_Б дает формулу R_Б для схемы автоматического смещения при обратной связи с коллектором.

Схема автоматического смещения при обратной связи с коллектором

\[I_К = \beta I_Б \qquad I_К \approx I_Э \qquad I_Э \approx \beta I_Б \]

\[V_{пит} — I_К R_К — I_Б R_Б -V_{БЭ} = 0\]

\[V_{пит} — I_Э R_К — (I_Э/ \beta) R_Б -V_{БЭ} = 0\]

\[V_{пит} -V_{БЭ} = I_Э R_К + (I_Э/ \beta) R_Б\]

\[V_{пит} -V_{БЭ} = I_Э (( R_Б / \beta) + R_К)\]

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К }\]

\[R_Б = \beta \left[ {V_{пит} -V_{БЭ} \over I_Э } — R_К \right] \]

Найдем необходимый резистор смещения при обратной связи с коллектором для тока эмиттера 1 мА, резистора нагрузки коллектора 4,7 кОм и транзистора с β=100. Найдем напряжение коллектора V_К. Оно должно быть примерно посередине между V_пит и корпусом.

\(\beta = 100 \qquad V_{пит} = 10 В \qquad I_К \approx I_Э = 1 мА \qquad R_К = 4,7 кОм \)

\[R_Б = \beta \left[ {V_{пит} — V_{БЭ} \over I_Э } — R_К \right] = 100 \left[ {10 — 0,7 \over 1 мА } — 4,7 кОм \right] = 460 кОм \]

\[ V_К = V_{пит} — I_К R_К = 10 — (1 мА) (4,7 кОм) = 5,3 В \]

Ближайший стандартный номинал к резистору 460 кОм для автоматического смещения при обратной связи с коллектором равен 470 кОм. Найдем ток эмиттера I_Э для резистора 470 кОм. Пересчитаем ток эмиттера для транзисторов с β=100 и β=300.

\(\beta = 100 \qquad V_{пит} = 10 В \qquad R_К = 4,7 кОм \qquad R_Б = 470 кОм \)

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К } = {10 -0,7 \over 470 кОм / 100 + 4,7 кОм } = 0,989 мА \]

\(\beta = 300 \)

\[I_Э = {V_{пит} -V_{БЭ} \over R_Б / \beta + R_К } = {10 -0,7 \over 470 кОм / 300 + 4,7 кОм } = 1,48 мА \]

Мы видим, что по мере того как коэффициент бета изменяется от 100 до 300, ток эмиттера увеличивается с 0,989 мА до 1,48 мА. Это лучше, чем в предыдущей схеме смещения с фиксированным током базы, где ток эмиттера увеличился с 1,02 мА до 3,07 мА. При изменении коэффициента бета смещение с обратной связью с коллектором в два раза стабильнее, чем смещение с фиксированным током базы.

Смещение эмиттера

Вставка резистора R_Э в схему эмиттера, как показано на рисунке ниже, вызывает уменьшение уровня сигнала на выходе, также известное как отрицательная обратная связь. Она препятствует изменениям тока эмиттера I_Э из-за изменений температуры, допустимых отклонений номиналов резисторов, изменений коэффициента бета или допустимых отклонений напряжения питания. Типовые допуски составляют: сопротивление резисторов – 5%, бета – 100-300, источник питания – 5%. Почему резистор эмиттера может стабилизировать изменение тока? Полярность падения напряжения на R_Э обусловлена V_пит на батарее коллектора. Полярность на выводе резистора, ближайшем к (-) клемме батареи, равна (-), а на выводе, ближайшем к клемме (+), равна (+). Обратите внимание, что (-) вывод R_Э подключен к базе через батарею V_смещ и R_Б. Любое увеличение тока через R_Э увеличит величину отрицательного напряжения, приложенного к цепи базы, уменьшая ток базы, что уменьшает ток эмиттера. Это уменьшение тока эмиттера частично компенсирует первоначальное увеличение.

Смещение эмиттера

\[V_{смещ} — I_Б R_Б — V_{БЭ} — I_Э R_Э = 0\]

\[I_Э = (\beta+1)I_Б \approx \beta I_Б\]

\[V_{смещ} — (I_Э / \beta) R_Б — V_{БЭ} — I_Э R_Э = 0\]

\[V_{смещ} — V_{БЭ} = I_Э ((R_Б / \beta) +R_Э)\]

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э }\]

\[R_Б / \beta +R_Э = {V_{смещ} — V_{БЭ} \over I_Э }\]

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right]\]

Обратите внимание, что на рисунке выше для смещения базы, вместо V_пит, используется батарея базы V_смещ. Позже мы покажем, что смещение эмиттера более эффективно с меньшей батареей смещения базы. Между тем, напишем уравнение закона напряжений Кирхгофа для контура цепи базы-эмиттера, обращая внимание на полярности компонентов. Подставим I_Б≅I_Э/β и решим уравнение для тока эмиттера I_Э. Это уравнение может быть решено для R_Б (смотрите выше).

Прежде чем применять формулы R_Б и I_Э (смотрите выше), нам нужно выбрать значения резисторов R_К и R_Э. R_К зависит от источника питания коллектора V_пит и тока коллектора, который мы хотим получить, и который, как мы предполагаем, приблизительно равен току эмиттера I_Э. Обычно точка смещения для V_К устанавливается равно половине V_пит. Хотя ее можно было бы установить и выше для компенсации падения напряжения на резисторе эмиттера R_Э. Ток коллектора – это то, что нам необходимо. Он варьируется от микроампер до ампер в зависимости от приложения и параметров транзистора. Мы выберем I_К = 1 мА, типовое значение для транзисторной схемы для малых сигналов. Мы вычисляем значение R_К и выбираем ближайшее стандартное значение. Как правило, хорошо подходит резистор эмиттера, который составляет 10-50% от резистора нагрузки коллектора.

\[V_К = V_{пит} / 2 = 10/2 = 5 В \]

\[R_К = V_К / I_К = 5/1 мА = 5 кОм \quad \text{(стандартный номинал 4,7 кОм)} \]

\[R_Э = 0,1 R_К = 0,1 (4,7 кОм) = 470 Ом \]

В нашем первом примере используем источник смещения с высоким напряжением V_смещ = V_пит = 10 В, чтобы показать, почему желательно более низкое напряжение. Определим стандартный номинал резистора. Рассчитаем ток эмиттера для β=100 и β=300. Сравним стабилизацию тока с предыдущими схемами смещения.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = V_{смещ} = 10 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {10 — 0,7 \over 0,001 } — 470 \right] = 883 кОм\]

Для рассчитанного сопротивления резистора R_Б 883 кОм ближайшим стандартным номиналом является 870 кОм. При β=100 ток эмиттера I_Э равен 1,01 мА.

\(\beta = 100 \qquad R_Б = 870 кОм \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {10 — 0,7 \over 870кОм / 100 + 470 } = 1,01 мА\]

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {10 — 0,7 \over 870кОм / 300 + 470 } = 2,76 мА\]

Токи эмиттера показаны в таблице ниже.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА

В приведенной выше таблице показано, что для V_смещ = 10 В смещение эмиттера не очень хорошо помогает стабилизировать ток эмиттера. Пример со смещением эмиттера лучше, чем предыдущий пример смещения базы, но не намного. Ключом к эффективности смещения эмиттера является снижение напряжения смещения базы V_смещ ближе к величине смещения эмиттера.

Какую величину смещения эмиттера мы сейчас имеем? Округляя, ток эмиттера, умноженный на сопротивление резистора эмиттера: I_ЭR_Э = (1 мА)(470) = 0,47 В. Кроме того, нам необходимо превысить V_БЭ = 0,7 В. Таким образом, на необходимо напряжение V_смещ > (0.47 + 0.7) В или > 1.17 В. Если ток эмиттера изменяется, это число изменится по сравнению с фиксированным напряжение смещения базы V_смещ, что приведет к коррекции тока базы I_Б и тока эмиттера I_Э. Нам подойдет V_Б > 1.17 В, равное 2 В.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 470 \right] = 83 кОм\]

Рассчитанный резистор базы 83 кОм намного меньше, чем предыдущий 883 кОм. Мы выбираем 82 кОм из списка стандартных номиналов. Токи эмиттера при R_Б = 82 кОм и коэффициентах β=100 и β=300 равны:

\(\beta = 100 \qquad R_Б = 82 кОм \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 82 кОм / 100 + 470 } = 1,01 мА\]

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 82 кОм / 300 + 470 } = 1,75 мА\]

Сравнение токов эмиттера для смещения эмиттера при V_смещ = 2 В и коэффициентах β=100 и β=300 с предыдущими примерами схем смещения показано в таблице ниже. И здесь мы видим значительное улучшение при 1,75 мА, хотя и не так хорошо, как 1,48 мА при обратной связи с коллектором.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В	1,01 мА	1,75 мА

Как мы можем улучшить эффективность смещения эмиттера? Либо увеличить резистор эмиттера R_Э или уменьшить напряжение источника смещения V_смещ, или и то, и другое. В качестве примера удвоим сопротивление резистора эмиттера до ближайшего стандартного значения 910 Ом.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 910 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 910 \right] = 39 кОм\]

Рассчитанное сопротивление R_Б = 39 кОм совпадает с одним из значений из стандартного списка номиналов. Пересчитывать I_Э для β = 100 нет необходимости. Для β=300 ток эмиттера равен:

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {2 — 0,7 \over 39 кОм / 300 + 910 } = 1,25 мА\]

Эффективность схемы смещения эмиттера с резистором эмиттера 910 Ом намного лучше. Смотрите таблицу ниже.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 470 Ом	1,01 мА	1,75 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 910 Ом	1,00 мА	1,25 мА

В качестве упражнения изменим пример смещения эмиттера, вернув резистор эмиттера на 470 Ом, и уменьшив напряжение источника смещения до 1,5 В.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 1,5 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {1,5 — 0,7 \over 0,001 } — 470 \right] = 33 кОм\]

Рассчитанное сопротивление R_Б = 33 кОм совпадает с одним из значений из стандартного списка номиналов. Поэтому пересчитывать I_Э для β = 100 нет необходимости. Для β=300 ток эмиттера равен:

\(\beta = 300 \)

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } = {1,5 — 0,7 \over 33 кОм / 300 + 470 } = 1,38 мА\]

В таблице ниже приведено сравнение результатов 1 мА и 1,38 мА с предыдущими примерами.

Сравнение токов эмиттера при β=100 и β=300.

Схема смещения	IЭ при β=100	IЭ при β=300
Схема смещения с фиксированным током базы	1,02 мА	3,07 мА
Схема смещения с обратной связью с коллектором	0,989 мА	1,48 мА
Смещение эмиттера, Vсмещ = 10 В	1,01 мА	2,76 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 470 Ом	1,01 мА	1,75 мА
Смещение эмиттера, Vсмещ = 2 В, RЭ = 910 Ом	1,00 мА	1,25 мА
Смещение эмиттера, Vсмещ = 1,5 В, RЭ = 470 Ом	1,00 мА	1,38 мА

Формулы для смещения эмиттера были повторены ниже с учетом внутреннего сопротивления эмиттера для лучшей точности. Внутреннее сопротивление эмиттера представляет собой сопротивление в цепи эмиттера внутри корпуса транзистора. Это внутреннее сопротивление r_Э оказывает большое влияние, когда (внешний) резистор эмиттера R_Э мал или даже равен нулю. Значение внутреннего сопротивления эмиттера является функцией тока эмиттера I_Э. Формула приведена ниже.

\[ r_Э = KT/I_Э m \]

где

• K=1.38×10^-23 Дж·К⁻¹ – постоянная Больцмана;
• T – температура в Кельвинах, берем ≅300;
• I_Э – ток эмиттера;
• m – для кремния изменяется от 1 до 2.

\[ r_Э = 0,026 В/I_Э = 26 мВ/I_Э \]

Ниже приведен вывод формул с учетом r_Э.

Схема смещения эмиттера с учетом внутреннего сопротивления r_Э

Более точные формулы смещения эмиттера могут быть получены при написании уравнения закона напряжений Кирхгофа для контура цепи базы-эмиттера. В качестве альтернативы, начнем с формулы I_Э, а затем перейдем в к формуле R_Б, заменив R_Э на r_Э + R_Э. Результаты показаны ниже.

\[V_{смещ} — I_Б R_Б — V_{БЭ} — I_Э r_Э — I_Э R_Э = 0\]

\[I_Э = (\beta+1)I_Б \approx \beta I_Б\]

\[V_{смещ} — (I_Э / \beta) R_Б — V_{БЭ} — I_Э r_Э — I_Э R_Э = 0\]

\[V_{смещ} — V_{БЭ} = I_Э (R_Б / \beta) + I_Э r_Э + I_Э R_Э\]

\[I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta + r_Э +R_Э }\]

\[R_Б / \beta + r_Э +R_Э = {V_{смещ} — V_{БЭ} \over I_Э }\]

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — r_Э — R_Э \right]\]

\[r_Э = 26 мВ / I_Э \]

Повторим расчет R_Б из предыдущего примера, но уже с учетом r_Э, и сравним результаты.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 2 В \qquad R_Э = 470 Ом \)

\( r_Э = 26 мВ / 1 мА = 26 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — r_Э — R_Э \right] = 100 \left[ {2 — 0,7 \over 0,001 } — 26 — 470 \right] = 80,4 кОм\]

Включение в расчеты r_Э приводит к более низкому значению сопротивления резистора базы R_Б, как показано в таблице ниже. Это значение находится ниже стандартного номинала 82 кОм, а не выше его.

Эффект от учета r_Э на расчет R_Б

rЭ?	Значение RБ
Без учета rЭ	83 кОс
С учетом rЭ	80,4 кОм

Конденсатор обхода R

_Э

Одна из проблем смещения эмиттера заключается в том, что значительная часть выходного сигнала падает на резисторе эмиттера R_Э (рисунок ниже). Это падение напряжения на резисторе эмиттера находится в последовательном соединении с базой и обладает полярностью, противоположной полярности входного сигнала. (Это похоже на схему с общим коллектором с коэффициентом усиления по напряжению < 1). Это уменьшение уровня сигнала сильно снижает коэффициент усиления по напряжению от базы до коллектора. Решение для усилителей сигналов переменного тока заключается в обходе резистора эмиттера с помощью конденсатора.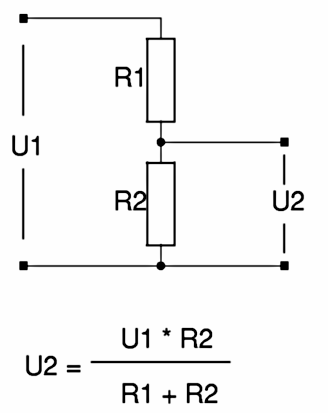 Это восстанавливает усиление переменного напряжения, поскольку конденсатор для сигналов переменного тока представляет собой короткое замыкание. Постоянный ток эмиттера всё еще будет уменьшаться на резисторе эмиттера, таким образом, стабилизация постоянного тока сохранится.

Конденсатор обхода требуется для предотвращения уменьшения усиления сигнала переменного напряжения

Какая величина емкости должна быть у конденсатора обхода? Она зависит от самой низкой частоты усиливаемого сигнала. Для радиочастот C_обхода может быть небольшим. Для аудиоусилителя с нижней частотой 20 Гц этот конденсатор будет большим. «Эмпирическое правило» для конденсатора обхода состоит в том, что реактивное сопротивление должно составлять 1/10 или меньше от сопротивления резистора эмиттера. Конденсатор должен быть выбран таким образом, чтобы поддерживать самую низкую частоту усиливаемого сигнала. Конденсатор для аудиоусилителя 20 Гц – 20 кГц равен:

\[X_C = { 1 \over 2 \pi f C }\]

\[C = { 1 \over 2 \pi f X_C }\]

\[C = { 1 \over 2 \pi 20 (470/10) } = 169 мкФ\]

Обратите внимание, что внутреннее сопротивление эмиттера r_Э не обходится конденсатором обхода.

Смещение делителем напряжения

Устойчивое смещение эмиттера требует низковольтного источника смещения базы (рисунок ниже). Альтернативой источнику базы V_смещ является делитель напряжения, питаемый источником питания коллектора V_пит.

Смещение делителем напряжения заменяет источник напряжения базы на делитель напряжения

Технология проектирования заключается в том, чтобы сначала разработать схему смещения эмиттера, затем преобразовать ее в схему смещения базы с помощью делителя напряжения, используя теорему Тевенина. Этапы графически показаны на рисунке ниже. Нарисуем делитель напряжения, не присваивая номиналов резисторов. Отделите делитель от базы (база транзистора является его нагрузкой). Примените теорему Тевенина, чтобы получить эквивалентные одно сопротивление Тевенина R_Тев и один источник напряжения V_Тев.

Теорема Тевенина преобразует делитель напряжения в один источник напряжения V_Тев и одно сопротивление R_Тев

Эквивалентное сопротивление Тевенина – это сопротивление от точки нагрузки (стрелка) при уменьшении напряжения батареи (V_пит) до 0 (земля). Другими словами, R1 || R2. Эквивалентное напряжение Тевенина представляет собой напряжение разомкнутой цепи (снятая нагрузка). Этот расчет осуществляется методом коэффициента деления делителя напряжения. R1 получается путем исключения R2 из пары формул для R_Тев и V_Тев. Ниже приведена формула расчета R1, исходя из значений R_Тев, V_Тев и V_пит. Обратите внимание, что R_Тев представляет собой R_Б, резистор смещения из схемы смещения эмиттера. Также ниже приведена формула расчета R2, исходя из значений R1 и R_Тев.

\[R_{Тев} = R1 || R2\]

\[{ 1 \over R_{Тев} } = { 1 \over R1} + { 1 \over R2}\]

\[V_{Тев} = V_{пит} \left[ {R2 \over R1+R2} \right]\]

\[\text f = { V_{Тев} \over V_{пит} }= \left[ {R2 \over R1+R2} \right]\]

\[{ 1 \over R_{Тев} } = { R2 + R1 \over R1 \cdot R2 } = { 1 \over R1 } \left[ { R2 + R1 \over R2 } \right] = { 1 \over R1 } \cdot { 1 \over \text f }\]

\[R1 = { R_{Тев} \over \text f } = R_{Тев} { V_{пит} \over V_{Тев}}\]

\[{ 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1}\]

Преобразуем предыдущий пример смещение эмиттера в смещение с помощью делителя напряжения.

Пример смещения эмиттера, преобразованный в смещение с помощью делителя напряжения

Эти значения были ранее выбраны или расчитаны для примера смещения эмиттера.

\(\beta = 100 \qquad I_Э \approx I_К = 1 мА \qquad V_{пит} = 10 В \qquad V_{смещ} = 1,5 В \qquad R_Э = 470 Ом \)

\[R_Б = \beta \left[ {V_{смещ} — V_{БЭ} \over I_Э } — R_Э \right] = 100 \left[ {1,5 — 0,7 \over 0,001 } — 470 \right] = 33 кОм\]

Подстановка значений V_пит, V_смещ и R_Б даст в результате значения R1 и R2 для схемы смещения с делителем напряжения.

\[V_Б = V_{Тев} = 1,5 В \]

\[R_Б = R_{Тев} = 33 кОм \]

\[R1 = R_{Тев} { V_{пит} \over V_{Тев}} = 33 кОм { 10 \over 1,5} = 220 кОм \]

\[{ 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1} = { 1 \over 33 кОм} — { 1 \over 220 кОм} \]

\[R2 = 38,8 кОм \]

Значение R1 равно стандартному значению 220 кОм. Ближайшее стандартное значение для R2, равного 38,8 кОм, рано 39 кОм. Это не сильно изменить I_Э, чтобы его рассчитывать.

Задача: Рассчитаем резисторы смещения для каскодного усилителя на рисунке ниже. V_Б2 – это напряжение смещения каскада с общим эмиттером. V_Б1 – это довольно высокое напряжение 11,5 В, потому что мы хотим, чтобы каскад с общей базой удерживал напряжение на эмиттере на уровне 11,5 – 0,7 = 10,8 В, примерно 11 В. (Это будет 10 В после учета падения напряжения на R_Б1.) То есть, каскад с общей базой является нагрузкой, заменяющей резистор, коллектора каскада с общим эмиттером. На нужен ток эмиттера 1 мА.

Смещение для каскодного усилителя

\( V_{пит} = 20 В \qquad I_Э = 1 мА \qquad \beta = 100 \qquad V_A = 10 В \qquad R_{нагр} = 4,7 кОм \)

\( V_{смещ1} = 11,5 В \qquad V_{смещ2} = 1,5 В \)

\[ I_Э = {V_{смещ} — V_{БЭ} \over R_Б / \beta +R_Э } \]

\[R_{Б1} = { V_{смещ} — V_{БЭ} \over I_Э / \beta } = { (V_{смещ1} — V_A) — V_{БЭ} \over I_Э / \beta } = { (11,5 — 10) — 0,7 \over 1 мА / 100 } = 80 кОм\]

\[R_{Б2} = { V_{смещ2} — V_{БЭ} \over I_Э / \beta } = { (1,5) — 0,7 \over 1 мА / 100 } = 80 кОм\]

Задача: Преобразуем резисторы смещения базы в каскодном усилителе в резисторы схемы смещения с делителем напряжения, питающимся от V_пит 20 В.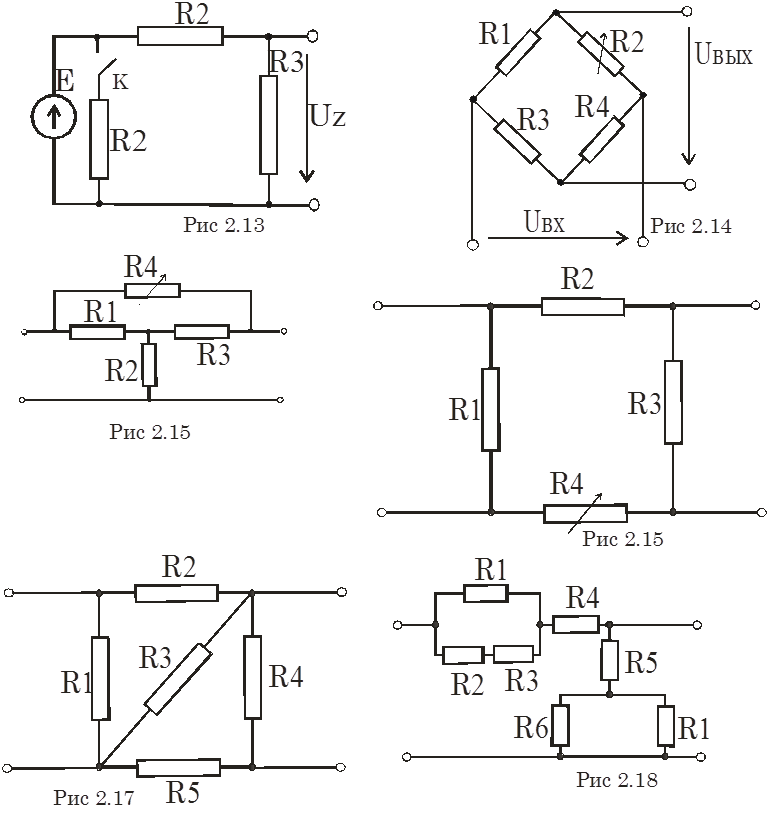

\[ R_{смещ1} = 80 кОм \]

\[ V_{смещ1} = 11,5 В \]

\[ V_{смещ} = V_{Тев} = 11,5 В \]

\[ R_Б = R_{Тев} = 80 кОм \]

\[ R1 = R_{Тев} { V_{пит} \over V_{Тев}} \]

\[ R1 = 80 кОм { 20 \over 11,5} = 139,1 кОм \]

\[ { 1 \over R2 } = { 1 \over R_{Тев}} — { 1 \over R1} \]

\[ { 1 \over R2 } = { 1 \over 80 кОм} — { 1 \over 139,1 кОм} \]

\( R2 = 210 кОм \)

\[ V_{пит} = V_{Тев} = 20 В \]

\[ R_{смещ2} = 80 кОм \]

\[ V_{смещ2} = 1,5 В \]

\[ V_{смещ} = V_{Тев} = 1,5 В \]

\[ R_Б = R_{Тев} = 80 кОм \]

\[ R3 = R_{Тев} { V_{пит} \over V_{Тев}} \]

\[ R3 = 80 кОм { 20 \over 1,5} = 1,067 МОм \]

\[ { 1 \over R4 } = { 1 \over R_{Тев}} — { 1 \over R3} \]

\[ { 1 \over R4 } = { 1 \over 80 кОм} — { 1 \over 1067 кОм} \]

\( R4 = 86,5 кОм \)

Окончательная схема показана в главе 9 «Практические аналоговые схемы» в разделе «Радиочастотные схемы» под названием «Каскодный усилитель класса A…».

Подведем итоги:

• Посмотрите на рисунок ниже.
• Выберите схему смещения.
• Выберите R_К и I_Э для вашего приложения. Значения R_К и I_Э обычно должны устанавливать напряжение коллектора V_К на 1/2 от V_пит.
• Рассчитайте резистор базы R_Б, чтобы получить необходимый ток эмиттера.
• Если необходимо, пересчитайте ток эмиттер I_Э для стандартных номиналов резисторов.
• Для схемы смещения с делителем напряжения выполните сначала расчет смещения эмиттера, а затем определите R1 и R2.
• Для усилителей переменного тока: конденсатор обхода, параллельный R_Э, улучшает усиление по переменному напряжению. Выберите X_C≤0,10R_Э для самой низкой частоты.

Формулы расчета смещения (вкратце)

Оригинал статьи:

Теги

Автоматического смещение с обратной связью с коллекторомБиполярный транзисторНапряжение смещенияОбучениеСмещение делителем напряженияСмещение с фиксированным током базыСмещение транзистораСмещение эмиттераЭлектроника

Сохранить или поделиться

Калькулятор делителя напряжения

Инструкция

Эта утилита вычисляет любую из четырех переменных, участвующих в простой схеме с двумя резисторами. делитель напряжения, заданные значения для каждой из трех других переменных. Переменные:

• В _в — (входное) напряжение, которое появляется на вершине делителя, измеряется в верхней части R ₁ относительно заземления цепи.
• R ₁ — Сопротивление (в Ом) верхнего резистора
• R ₂ — Сопротивление (в Ом) нижнего резистора
• В _вых — Напряжение, которое появляется на стыке R ₁ и R ₂ , измеряется относительно земли цепи.

Пример

Обычно требуется вычислить одно из двух сопротивлений, учитывая указанное V _в , желаемое V _из и одно из двух сопротивлений.В этом случае вы вводите два напряжения и известный резистор и утилита решит неизвестный резистор

Однако рассмотрим следующий случай:

Вы ищете неисправность в цепи и обнаруживаете, что V _из делителя напряжения на 5 Вольт V _в , разработанный с двумя резисторами 10k, измеряет только 0,45 В (вы ожидали увидеть 2,5 В).

В этом случае вы подозреваете, что использовали неверный номинал резистора.Вы должны ввести одно из рассчитанных значений резистора, ввести два напряжения и найти значение резистора. Изучение рассчитанного значения может свидетельствовать о том, что вы, возможно, неправильно поняли значение резистора. Например, в делителе напряжения, состоящем из двух резисторов 22,1 кОм, для деления 5 В на 2,5 В, вы обнаружите, что на самом деле на выходе было 0,45 В. Вы думаете, что у вас может быть неправильное значение для одного из резисторов. Итак, вы вводите 5 В и 0,45 В (как V _в и V _из соответственно), установите R ₁ на проектные 22 100 Ом и найдите R ₂ , и вуаля! — вы получаете значение 2100 Ом для R ₂ , что предполагает, что вы могли ошибочно заменить 2.Резистор 21кОм для резистора 22.1кОм!

Калькулятор

Резистивный разветвитель Адамса

Нажмите здесь, чтобы перейти на нашу главную страницу резистивных разветвителей

Нажмите здесь, чтобы ознакомиться с резистивным разветвителем Owen, он также может обеспечивать неравные разветвления

Нажмите здесь, чтобы перейти на нашу главную страницу о неравных сплиттерах

Вот ссылка на классный калькулятор, который предоставит вам номиналы резисторов делителя Адамса. Спасибо Брайану!

На этой странице описывается резистивный сплиттер с неравным делением, разработанный Грегом Адамсом. Впервые мы столкнулись с ним на веб-сайте, которого больше не существует. Они не дали уравнений в закрытой форме для любого из элементов, только несколько примеров номиналов резисторов для трех разных разветвителей. Позднее разветвитель был полностью описан в статье Грега Адамса в мартовском выпуске журнала High Frequency Electronics за 2007 год. (Спасибо Дэвиду за исправление ссылки!) В этой статье есть уравнения для решения для резисторов.Грег описывает умное упрощение, которое мы упустили из виду! Мы спросили Грега, каково значение номенклатуры Rs, Rt и Ru. Rs был назван потому, что это последовательный резистор, а Rt и Ru — просто следующие буквы в алфавите!

Обратите внимание, что на изображении ниже резистор последовательно подключен к порту 2. Его там быть не должно… Порт 2 должен напрямую подключаться к соединению RT и Ru. Спасибо Брайану за указание на это! Мы исправим изображение в один прекрасный день.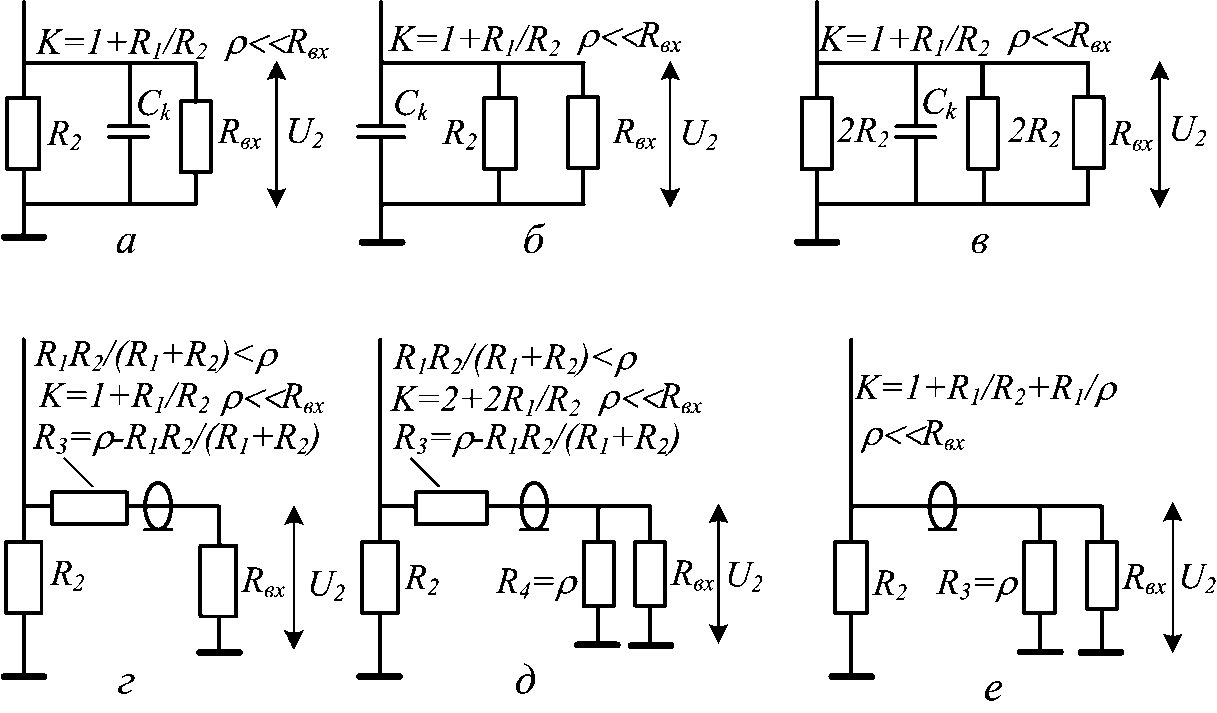 Между тем, все эти годы он служил Mountweazel…

Мы использовали его уравнения для определения значений резистора делителя на основе вносимых потерь от входа до первого порта. Калькулятор в нижней части страницы рассчитает все номиналы резисторов для заданных вносимых потерь. Мы нормализовали все значения резисторов к эталонному импедансу (Zo) сети, чтобы получить более общий результат. Сеть в том виде, в котором она сконфигурирована, не может быть реализована для входа более 6 дБ, и в результате калькулятор выдаст сообщение об ошибке.

Каждый параметр производительности и конструкции сплиттера однозначно определяется значением выхода первого сплиттера, поэтому мы сэкономили вам время и нанесли результирующее разделение на порт 2 и общий КПД схемы ниже.

Аналогично, мы построили нормализованные значения резисторов, используемых в разветвителе, в зависимости от разделения мощности первого выходного порта.

У нас есть информация от Энди о дополнительных степенях свободы с резистивными делителями:

Калькулятор делителя напряжения — Рассчитайте номиналы резисторов в схеме делителя напряжения с двумя резисторами.

Калькулятор делителя напряжения. Рассчитайте номиналы резисторов в цепи делителя напряжения с двумя резисторами.

Делитель напряжения на два резистора является одной из самых основных и распространенных схем в электронике. Часто это первая схема, которую изучает новичок. Делитель напряжения превращает большое напряжение в меньшее. Как это работает, соотношение резисторов (R1 и R2) делит вход напряжение до более низкого выходного напряжения. Выходное напряжение представляет собой долю входного напряжения, и эта доля равна R2, деленному на сумма R1 + R2.Формула VOUT = VIN * (R2 / (R1 + R2)). Калькулятор делителя напряжения предполагает, что вы знаете любые три значения схемы делителя напряжения. Используйте калькулятор ниже, чтобы вычислить значение отсутствующего параметра.

Делитель напряжения общего назначения

Делители напряжения обычно используются для уменьшения входного напряжения на канал АЦП. Например, если вы хотите прочитать напряжение источника питания на 12 вольт, но ваш АЦП имеет максимальный входной уровень 5 вольт, делитель напряжения уменьшит напряжение до безопасный уровень.

Многие датчики являются резистивными, и АЦП не может получить от них правильные показания. Добавляя резистор к резистивному датчику, вы создаете делитель напряжения. Когда выход делителя напряжения известен, Вы можете рассчитать сопротивление датчика.

Используя делитель напряжения в сочетании с АЦП, можно считывать показания всех видов датчиков.

• тримпоты
• слайдеры
• аккумуляторы
• термисторы
• джойстики
• многое другое

Когда не следует использовать делитель напряжения

Схемы делителя напряжения не подходят для понижения напряжения для использования в качестве источника питания.Мало того, что это было бы ужасно неэффективно, достаточный ток, протекающий через R1, может привести к сгоранию резистора. Как правило, никогда не используйте делитель напряжения. в качестве источника напряжения для всего, что требует даже скромного количества энергии. Если вам нужно понизить напряжение, чтобы использовать его в качестве источника питания, обратите внимание на стабилизаторы напряжения или импульсные источники питания.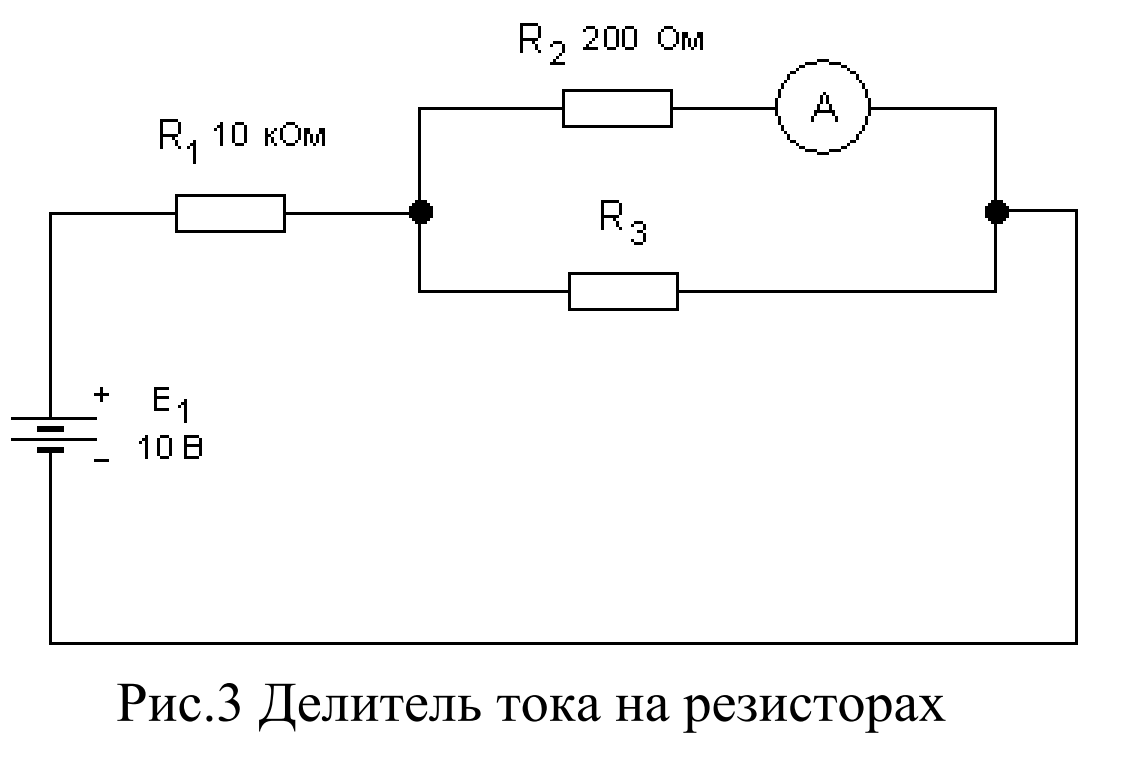

Также обязательно ознакомьтесь с нашим Инструментом преобразования конденсаторов мкФ в нФ в пФ, который поможет вам выбрать правильные конденсаторы для вашего следующего проекта.

Делители напряжения | Абсолютная книга по электронике

Ultimate Electronics: практическое проектирование и анализ схем

---

Чрезвычайно распространенная конфигурация резисторов 2+. Приближения, рекомендации по проектированию. Пример контроллера тока светодиода. 22 мин чтения

Делители напряжения — это просто определенные комбинации последовательно соединенных резисторов при подключении к идеальным источникам напряжения и тока.

В то время как математика решения этих цепей была рассмотрена в предыдущих разделах, делители напряжения заслужили свое собственное название, потому что они появляются достаточно часто, чтобы быть полезным сокращением при анализе многих больших цепей.(Поскольку более сложные подсхемы могут быть аппроксимированы как одиночный резистор, термин и методы здесь также могут применяться более широко, чем просто резисторы.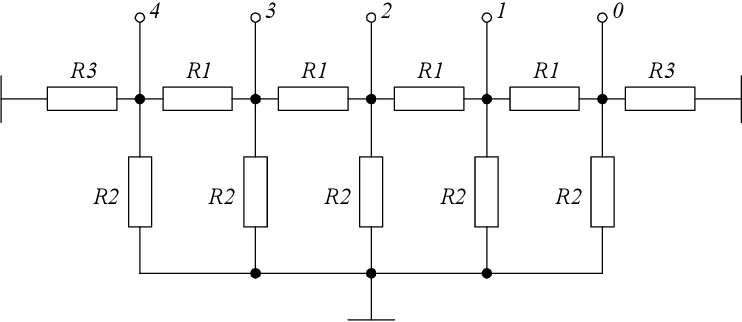 ) Мы начнем с идеального случая, рассмотрим неидеальный случай, а затем покажем, когда аппроксимации полезны при проектировании и анализе.

Когда вы видите, как опытный инженер-электрик бросает быстрый взгляд на аналоговую схему и быстро определяет, что происходит, он, скорее всего, делает в уме аппроксимации делителя напряжения, иногда даже не осознавая этого!

---

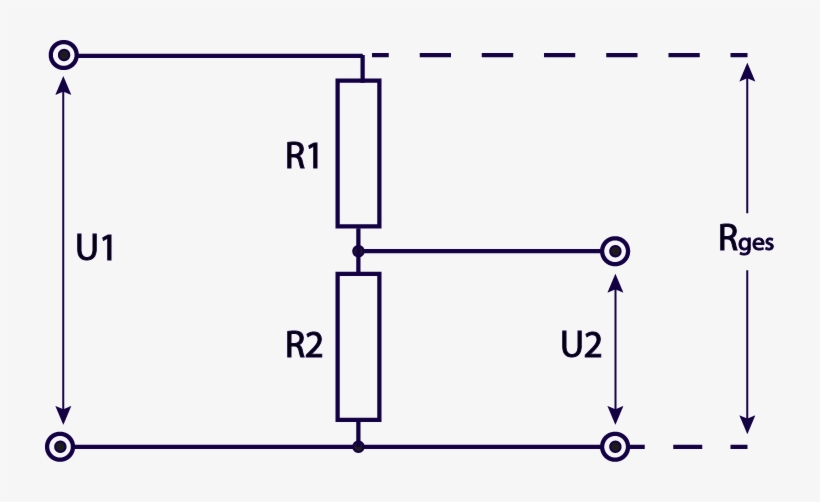
Идеальный делитель напряжения состоит из двух последовательных резисторов.Физически это иногда реализуется в виде потенциометра, который разделяет один физический резистор на две части с помощью физически подвижного проводящего центрального контакта. Но чаще всего это два дискретных постоянных резистора.

Когда на пару подается напряжение, выходное напряжение составляет некоторую часть входного напряжения:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Измените сопротивления и посмотрите, как изменится выходное напряжение в ответ.

Это можно увидеть, используя закон Кирхгофа для напряжения плюс закон Ома, чтобы записать сумму разностей напряжений на контуре:

vin-iR1-iR2=0vin=i(R1+R2)vinR1+R2=i

Теперь мы можем записать закон Ома для R2, ​​vout=iR2 (поскольку другой конец R2 заземлен), и подставим в наше выражение для контурного тока i выше:

выход=вин(R2R1+R2)

Для удобства выделим дробь f , коэффициент делителя напряжения :

ф=R2R1+R2

, где vout=vin⋅f . Поскольку сопротивления не могут быть отрицательными, 0≤f≤1 .

Есть несколько особых случаев, о которых стоит подумать:

1. В относительно распространенном частном случае двух одинаковых сопротивлений R1=R2 , отношение f=12 .
2. Если R1≫R2 отношение f→0 .
3. Если R1≪R2 отношение f→1 .

Эти аппроксимации невероятно полезны, и более подробные версии разработаны в Алгебраических аппроксимациях.

Делитель напряжения всегда выдает уменьшенную версию входного напряжения.Вот пример с делителем напряжения, управляемым синусоидой от функционального генератора:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему и посмотреть на взаимосвязь между входными и выходными сигналами.

---

Поскольку делитель напряжения выдает мультипликативно масштабированную версию входного сигнала, если мы возьмем логарифм обеих частей (по любому основанию), мы обнаружим, что коэффициент делителя напряжения превращается в аддитивную константу:

vout=vin⋅flog(vout)=log(vin)+log(f)

При f≤1 , всегда будет так, что log(f)≤0 .

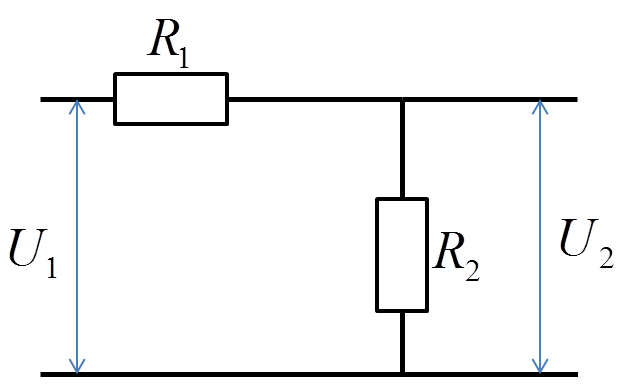
Вот пример с функциональным генератором, управляющим делителем напряжения, где мы отображаем напряжения в логарифмической шкале:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Обратите внимание, как в логарифмическом масштабе две трассы кажутся просто сдвинутыми по вертикали на постоянное смещение. В разделе «Расширенный график» измените его обратно на линейный масштаб, чтобы увидеть исходный сигнал.

В этом примере мы позаботились о том, чтобы наш входной сигнал был строго положительным, но вы также можете применить ту же логику к амплитуде сигнала, которая становится как положительной, так и отрицательной во времени.В этом случае делитель напряжения дает сдвиг графика амплитуды в частотной области:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему.

При выполнении этой симуляции входное и выходное напряжения строятся с отклонением −6 дБ. сдвиг между входной и выходной амплитудой. Это −6 дБ потому что амплитуда напряжения уменьшается вдвое. Дополнительную информацию см. в разделе «Порядки величины, логарифмические шкалы и децибелы».

---

Делители напряжения могут быть изготовлены с N последовательные резисторы иметь N−1 узлы между ними.Пока нет тока, входящего или выходящего из цепи делителя напряжения, с точки зрения какого-либо конкретного отвода, резисторы «вверху» можно объединить в один, а резисторы «внизу» — в другой.

Это упрощает создание большого количества коэффициентов напряжения для одного входа. Например:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему.

На приведенной выше схеме используются пять последовательно соединенных резисторов. Он превращает 12-вольтовый вход в четыре разных выхода, которые могут быть полезны в блоке питания компьютера.

Поскольку это последовательная цепь, в ней присутствует только один ток, и его легко определить, рассматривая резисторы, включенные последовательно:

итого=vin∑R

Тогда падение напряжения на одном резисторе равно:

Δvn=Rn⋅итого

и долю полного падения напряжения на любом одном резисторе Rn это:

fn=Δvnvinfn=Rn⋅totalvinfn=(Rnvin)(vin∑R)fn=Rn∑R

Доля падения напряжения на одном резисторе — это просто отношение его сопротивления к сумме всех сопротивлений.

Для пяти последовательно соединенных резисторов мы можем рассчитать напряжения в каждом узле (относительно земли), взглянув на отношение сопротивления «ниже» этого узла (т. е. между этим узлом и землей) к общему сопротивлению цепи. В этом примере с узлами и резисторами, как указано выше:

vA=(Δv1)=vin(f1)vB=(Δv1+Δv2)=vin(f1+f2)vC=(Δv1+Δv2+Δv3)=vin(f1+f2+f3)vD=(Δv1+Δv2+ Δv3+Δv4)=vin(f1+f2+f3+f4)

Когда мы разработаем решение для схемы выше:

vA=vin(R1R1+R2+R3+R4+R5)=2.5 VvB=vin(R1+R2R1+R2+R3+R4+R5)=3,3 VvC=vin(R1+R2+R3R1+R2+R3+R4+R5)=5,0 VvD=vin(R1+R2+R3+R4R1) +R2+R3+R4+R5)=9,0 В

Конечно, для решения задач мы выбрали определенные значения, которые было легко вычислить вручную: вы, наверное, заметили, что мы выбрали vin=12 В. и ∑R=12 кОм так что это всего = 1 мА .

Как мы увидим позже, этот тип схемы не очень энергоэффективен и не сможет обеспечить большой ток. Тем не менее, это был бы потенциально допустимый способ преобразования одного опорного напряжения в ряд других пропорциональных опорных напряжений, которые затем можно было бы использовать как часть контура обратной связи в эффективной конструкции импульсного источника питания.

---

Одним из распространенных способов быстрого решения проблемы является обнаружение, когда резисторы в делителе напряжения являются целым кратным друг другу.

Например, если R1=100 Ом, R2=300 Ом , тогда соотношение 3 к 1. Всякий раз, когда соотношение 3 к 1, независимо от фактических значений, мы будем иметь f=R2R1+R2=34. .

Это также помогает в дизайне. Если вы пытаетесь получить известную долю напряжения f которую можно выразить в виде доли целых чисел, то можно быстро вычислить необходимое соотношение сопротивлений.

Например, если вы пытаетесь нажать f=0,4=25 , вы можете искать значения резисторов, где R2 = 2x, R1 = 3x для любого значения х , так что R2R1=23 . (Продолжайте читать ниже, чтобы узнать, как мы выбираем x !)

В некоторых ситуациях прототипирования, если целые числа в числителе и знаменателе достаточно малы, вы можете просто использовать пять резисторов с одинаковым номиналом, поставив два последовательно, чтобы сформировать R2. и три последовательно для R1 .

---

Когда мы включаем источник управляющего напряжения, мы можем рассмотреть, что происходит, когда мы смотрим на промежуточный вывод делителя напряжения, чтобы найти эквивалентную схему Thevenin:

Напряжение холостого хода — это просто напряжение, которое мы измерили бы на этих клеммах без внешнего тока, то есть просто дробное входное напряжение, которое мы рассчитали выше:

Veq=vout,unloaded=vin(R2R1+R2)

Как только мы начнем позволять внешнему току течь к этим клеммам и от них, измеренное напряжение изменится.Как описано в разделе Thevenin, мы можем вставить тестовый источник тока и установить все независимые источники на ноль, чтобы вычислить эквивалентное сопротивление:

Отсюда видно, что эквивалентное сопротивление равно сопротивлению двух параллельно включенных резисторов:

Треб.=R1//R2=R1R2R1+R2

Таким образом, двухрезисторный делитель напряжения выглядит как однорезисторный эквивалент Тевенина:

---

Мы только что преобразовали двухрезисторный делитель напряжения в однорезисторную эквивалентную схему Thevenin, которая имеет идентичное поведение кривой ток-напряжение по отношению к некоторой внешне подключенной нагрузке. Но когда у нас есть эквивалентная схема Thevenin, часто самое полезное, что можно сделать с ней, — это подключить ее к какой-нибудь внешней нагрузке. Если эта нагрузка представляет собой резистор, то мы только что сформировали новый делитель напряжения .

Например, мы могли бы взять схему с тремя резисторами слева и рассмотреть, что R1 и R2 образуют делитель напряжения, а затем заменить их эквивалентом Thevenin:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему.

Вы должны запустить моделирование, чтобы убедиться, что через R3 протекает одинаковый ток в обоих случаях.

Замена делителя напряжения его эквивалентом Thevenin может сама по себе образовать новый делитель напряжения, который снова может быть решен таким же образом. Это отличная техника решения проблем.

---

Приведенный выше пример, эквивалентный Thevenin, особенно полезен, потому что он поднимает концепцию , нагружающей : что происходит, когда токовая «нагрузка» снимается со среднего вывода делителя напряжения?

В математике идеального делителя напряжения, приведенной выше, мы рассчитали выходное напряжение как функцию входного напряжения vin. и коэффициент делителя напряжения f=R2R1+R2 Только.Но в этом расчете предполагалось, что один и тот же ток i протекал через оба резистора R1 и R2.

В нагруженном делителе напряжения этого нет: есть какой-то внешний ток i3 берется из середины делителя напряжения:

В результате, если i3≠0 , то также будем иметь i1≠i2 . Это нарушает основное предположение, сделанное нами ранее для идеальных делителей напряжения.

Обратите внимание, что ни схема, ни уравнения не «знают», что R3 является внешней нагрузкой, а R2 является частью исходного делителя напряжения.Оба резистора подключены к одной и той же паре узлов, и математика работает одинаково, если мы поменяем имена, которые мы даем. Тем не менее, проводя границу, отделяющую внутреннее от внешнего, и думая об этом таким образом, нагруженные делители напряжения становятся полезными для проектирования и анализа схем, как мы увидим ниже.

Теперь, когда мы применяем наши правила для решения систем цепей, мы получаем разные значения тока в разных ветвях цепи. Наше уравнение закона тока Кирхгофа плюс наши два уравнения закона Ома образуют следующую систему из трех уравнений:

i1=i2+i3vin-vout=i1R1vout=i2R2

Мы хотим решить эту систему для одного выражения vout как функция vin,R1,R2 и i3 .(Мы решили лечить i3 как независимая переменная, поэтому мы можем видеть влияние тока нагрузки напрямую, а не связывать его с напряжением через сопротивление R3 .) Решить это вручную очень полезно, чтобы вы могли видеть, как подход Solving Circuit Systems дает тот же ответ, что и подход Thevenin, описанный выше, поэтому, пожалуйста, возьмите лист бумаги и следуйте инструкциям.

Сначала мы перестроим несколько уравнений, приняв i2=i1−i3. из первого уравнения и подставляя в третье, чтобы получить:

vвых = (i1−i3)R2

Мы также возьмем второе уравнение и разделим обе части на R1 :

i1=вин-воутR1

Мы можем объединить эти два значения, заменив i1 на in :

vout=(vin-voutR1-i3)R2

Теперь нам осталось заняться алгеброй. Распространение R2 :

vвых=(вин-воут)(R2R1)-i3R2

Собрать воут члены в левой части:

vвыход(1+R2R1)=vin(R2R1)−i3R2

Заменить (1+R2R1)=(R1+R2R1) :

vвых(R1+R2R1)=vin(R2R1)−i3R2

И разделить его, чтобы изолировать vout :

vout=vin(R2R1)(R1R1+R2)−i3R2(R1R1+R2)vout=vin(R2R1+R2)−i3(R1R2R1+R2)

Это уравнение описывает выходное напряжение нагруженного делителя напряжения.

Посмотрите внимательно на коэффициенты vin и i3 :

1. Коэффициент на вин , (R2R1+R2) , это просто коэффициент делителя напряжения f мы нашли ранее в незагруженном корпусе.Если i3=0 , то делитель разгружается, и общее уравнение упрощается и становится таким же, как мы нашли в начале этого раздела.
2. Коэффициент для i3 равно (R1R2R1+R2)=R1//R2 , параллельное сопротивление двух резисторов! (Да, параллельно — хотя R1 и R2 кажутся в серии в делителе напряжения!) Это тот же нелогичный результат, который мы только что нашли в разделе «Эквивалент Thevenin» выше.

Этот пример показывает, что для решения схемы из KCL и KVL может потребоваться немного алгебраической работы, но это всегда работает и всегда дает правильный ответ.Если вы не уверены, правильно ли вы применяете эквивалентный процесс Thevenin, вы всегда можете вставить тестовый текущий источник i3. и приступайте к решению схемы вручную.

---

Какая интуиция стоит за током нагрузки в нагруженном делителе напряжения, вызывающим падение напряжения, пропорциональное параллельному сопротивлению R1 и R2, которые (до рассмотрения нагрузки) кажутся последовательными?

Быстрый способ запомнить это — рассмотреть крайние случаи и работать в обратном порядке.

В одном крайнем случае рассмотрим R1=0 или R2=0 (но не оба сразу). В этом случае выходное напряжение вообще не изменится с i3 . Нулевое сопротивление параллельно с ненулевым сопротивлением всегда равно нулю. В этом крайнем случае нагрузка напрямую подключена (с нулевым сопротивлением) к одному концу источника напряжения.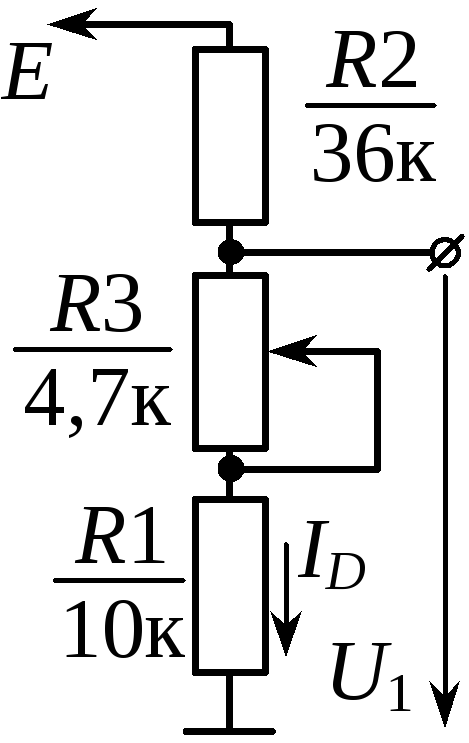

Вот как упрощается нагруженный делитель напряжения при нулевом сопротивлении:

В качестве другой крайности рассмотрим R1=∞ или R2=∞ (но не оба сразу).В этом случае делитель напряжения в основном отключен с одного конца. Бесконечное сопротивление параллельно с конечным сопротивлением всегда равно конечному сопротивлению.

(Для параллельных сопротивлений помните, что общее сопротивление всегда на 90 277 меньше, чем 90 278, чем 90 277 наименьших 90 278 отдельных сопротивлений. Или, что то же самое, общая проводимость всегда на 90 277 больше, чем 90 278, чем 90 277 наибольших 90 278 отдельных проводимостей.)

Вот как упрощается нагруженный делитель напряжения при предельном бесконечном сопротивлении:

Уравнение идеального делителя напряжения правильно сводится к этим случаям, если падение напряжения из-за нагрузки пропорционально параллельному сопротивлению R1//R2 .

Как насчет среднего случая, когда оба сопротивления конечны? Один из способов думать об этом состоит в том, что небольшое увеличение тока нагрузки i3 имеет двойной эффект: увеличение i1 и уменьшение i2 . На самом деле ни один из двух токов i1 или i2 нужно менять на полную величину изменения в i3 , потому что они буквально делят разницу (с обратным знаком, но это просто вопрос маркировки токов):

Δi1−Δi2=Δi3

Например, если R1=R2 , то они поделят разницу поровну, при этом Δi1=12Δi3 , а Δi2=−12Δi3 .Поскольку величина изменения тока через каждый резистор меньше, его изменение напряжения также меньше, просто из-за закона Ома.

На этом рисунке показано, как ток нагрузки делится поровну между обоими резисторами делителя напряжения, когда R1=R2 :

Мы можем смоделировать этот эффект численно:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Обратите внимание, что наклон отдельных токов для R1 и R2 вдвое меньше, чем для испытательного тока.Измените сопротивление и посмотрите, как изменится поведение в ответ.

---

На практике практически все делители напряжения в реальном мире нагружены: что-то будет подключено к средней клемме, чтобы промежуточная точка была полезной, иначе мы просто использовали бы один резистор или вообще не использовали бы его!

Однако, как видно из уравнения нагруженного делителя напряжения, математика для определения vout становится значительно сложнее, если ввести ток нагрузки i3 .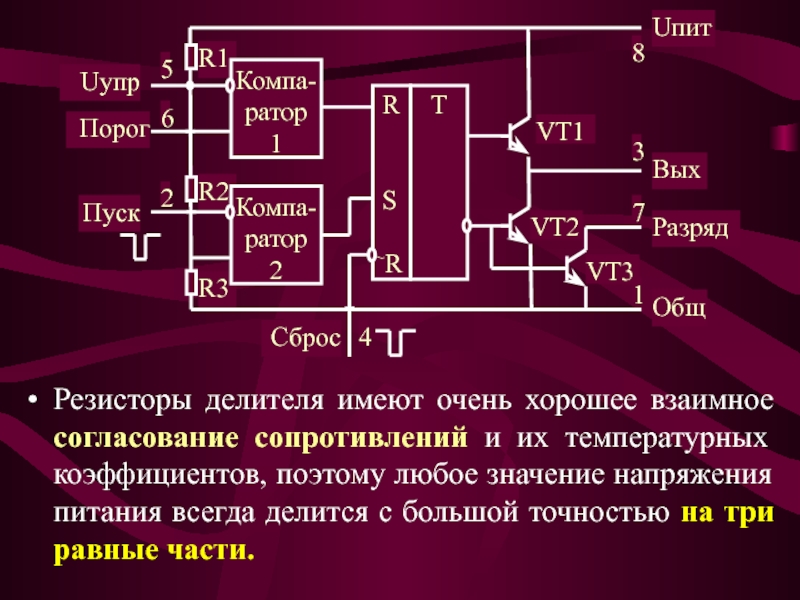 Было бы неплохо знать, когда безопасно и небезопасно аппроксимировать делитель напряжения как приблизительно без нагрузки.

Ответ следует из рассмотрения дополнительного падения напряжения из-за нагрузки как погрешности аппроксимации verr :

vвыход=vin(R2R1+R2)−i3(R1R2R1+R2)vвых=vвых,идеал+верр

Если мы сосредоточимся только на термине ошибки:

верр=-i3(R1R2R1+R2)верр=-i3(R1//R2)

Если мы знаем максимальную величину тока нагрузки |i3,max| , и мы можем определить максимальную ошибку напряжения |verr,max| мы готовы терпеть, тогда мы можем поставить ограничение на (R1//R2) :

|i3,max|(R1//R2)≤|verr,max|(R1//R2)≤|verr,max||i3,max|

Если наша допустимая погрешность напряжения мала, сопротивления также должны быть малы.Если наш допустимый ток нагрузки велик, это также заставит сопротивления быть маленькими. Определение этого с точки зрения максимальных допусков означает, что даже если фактический ток нагрузки варьируется, пока он меньше, чем максимальный ток нагрузки, на который мы рассчитывали, мы можем быть уверены, что наш делитель напряжения все еще будет находиться в пределах наших проектных ограничений.

Это невероятно полезно на практике, потому что это означает, что нам не нужно проектировать всю нашу систему сразу. Аппроксимации позволяют разделить большую проектную задачу на ряд более мелких, где мы можем решать по одной части за раз. У этого есть два преимущества:

1. Более быстрое проектирование. Часто проще решить две маленькие подзадачи, чем одну большую.
2. Более надежная работа. Решение, которое мы получаем, разбивая нашу систему на модули с границами ошибок, может быть более терпимым к непреднамеренной дисперсии компонентов, потому что оно уже было разработано с расчетными границами ошибок. Напротив, оптимизированное решение «все сразу» может оказаться неожиданно хрупким, если какой-то компонент отличается от желаемого значения на 5 %.(Этот риск хрупкости становится особенно распространенным, когда мы начинаем добавлять какие-либо нелинейные элементы схемы, такие как транзисторы и усилители.)

---

Давайте попробуем решить типичную задачу проектирования, где нам нужно спроектировать делитель напряжения как часть более крупной схемы.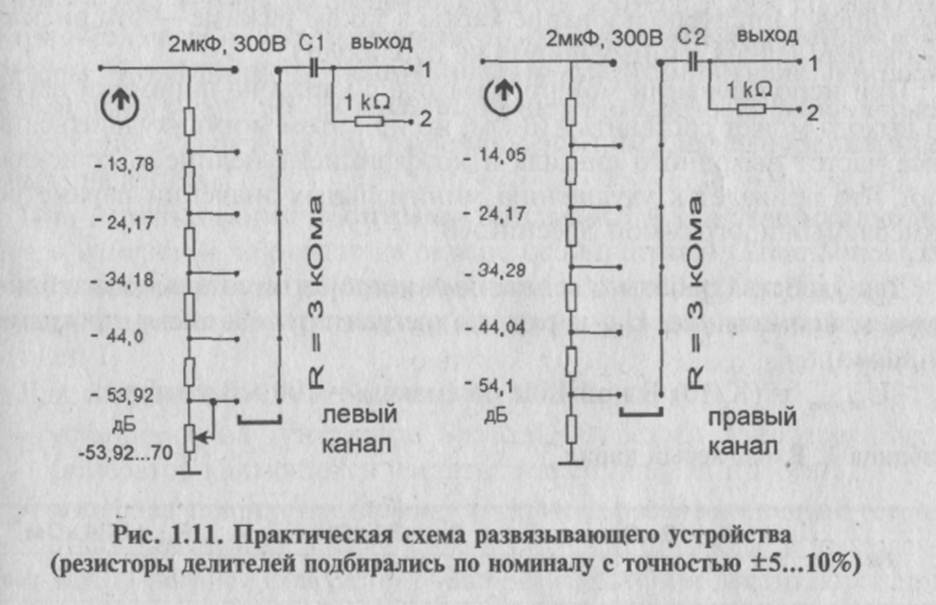

Мы разработаем контроллер постоянного тока для светодиода (светоизлучающего диода), где мы хотим убедиться, что светодиод потребляет ток не более 20 мА, чтобы предотвратить его перегорание. Производственные вариации означают, что мы не знаем точного напряжения светодиода, поэтому нам нужно управление светодиодом на основе тока, даже если у нас есть регулируемое напряжение в качестве источника питания.

При сохранении подробностей для следующей главы, один из способов создать практичный источник тока — использовать BJT (двухполюсный переходной транзистор) с резистором для обратной связи. Нам нужно зафиксировать один вывод (базу) этого транзистора на 1,7 В, а у нас блок питания на 5 В. Для этого мы можем использовать делитель напряжения:

Мы разделили схему на три блока: источник питания и делитель напряжения (V1, R1 и R2), источник тока на основе транзисторов (Q1 и RE) и нагрузку, которой мы пытаемся управлять (D1). ).

Теперь нам нужно найти неизвестные резисторы R1 и R2, чтобы установить соответствующее базовое напряжение смещения для нашего транзистора.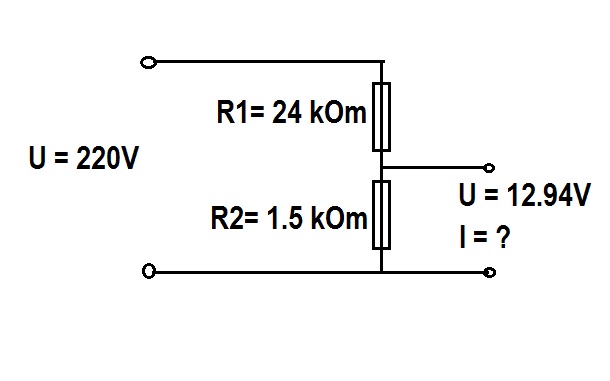 В реальности делитель напряжения нагружен, что требует гораздо больше информации для расчета точного базового напряжения. Согласно приведенному выше уравнению делителя напряжения, нам также нужно знать ток базы, и это быстро усложнится, поскольку он циклически зависит от сопротивлений R1 и R2, а также от свойств самих транзистора и светодиода. Сложность вычислений растет экспоненциально быстро!

Вместо этого давайте предположим, что мы можем рассматривать делитель напряжения R1 и R2 как , приблизительно разгруженный , и достаточно просто найти желаемое выходное напряжение.Если делитель напряжения не нагружен:

voutvin=f=R2R1+R2f(R1+R2)=R2fR1=R2(1−f)R2R1=f1-fR2R1=voutvin1-voutvinR2R1=voutvin-vout

, значит, если мы знаем, что vin=5 В и vвых=1,7 В , тогда:

R2R1=1,75−1,7R2R1=0,52

Сделав предположение, что мы можем решить делитель напряжения как ненагруженный, мы быстро нашли отношение R2R1 .

Это говорит нам о относительных сопротивлений двух резисторов в делителе напряжения, чтобы получить желаемое напряжение. Однако мы еще не установили их 90 277 абсолютных значений 90 278: мы могли бы выбрать (R1 = 10 Ом, R2 = 5,2 Ом) или (R1=1 МОм, R2=520 кОм) и оба удовлетворили бы нашему требованию отношения.

Выбор того, где зафиксировать эти абсолютные значения, имеет практические инженерные компромиссы в обеих крайностях:

1. Если сопротивления слишком малы: сам делитель напряжения будет потреблять большой ток (i=5 VR1+R2 ) и мощность (P=(5 В)2R1+R2 ). Это расточительно: это увеличивает наши требования к источнику питания или быстрее разряжает нашу батарею, и мы должны начать думать о тепловыделении резистора и температурных коэффициентах, а также о физических ожогах пользователей, касаясь этих горячих резисторов!
2. Если сопротивления слишком велики: , то ошибка напряжения из-за нагрузки |verr|=i3(R1//R2) будет недопустимо большим, и мы не получим ожидаемую уставку напряжения.

Как мы выбираем?

У нас есть инженерный компромисс между энергопотреблением и точностью. Это типичный инженерный компромисс, на который должен пойти проектировщик. Правильным подходом к проектированию было бы разумное ограничение желаемого уровня точности и обеспечение разумного результата по энергопотреблению.

Допустим, мы хотим, чтобы желаемое напряжение было в пределах 5% от расчетного. Это число в 5% может показаться произвольным.Разумный способ выбрать бюджет ошибок состоит в том, чтобы рассмотреть значения разных порядков с обеих сторон: 50% — это, очевидно, слишком большая ошибка почти во всех обстоятельствах; 10%, вероятно, было бы хорошо, если бы мы действительно не заботились о точности; 1% или 0,5% потребовали бы от нас гораздо большей точности в отношении других компонентов нашей системы, таких как сами светодиоды и транзисторы, не говоря уже о резисторах, точность которых обычно составляет всего 1% или 5%. 5% приятно посередине! (Это обычно используемая отправная точка для цели дизайна, если у вас нет причин выбирать иное.)

Выбрав 5% в качестве максимально допустимой погрешности напряжения, мы можем сказать:

vвых=1,7 В±5%vвых=1,7 В±85 мВ|verr|≤85 мВ

Из вышеизложенного мы знаем, что для нагруженного делителя напряжения |verr|=i3(R1//R2) . Мы еще не рассмотрели транзисторы с биполярным соединением, такие как Q1, но сейчас просто предположим, что базовый ток (который равен i3 ) составляет небольшую долю тока нагрузки (коллектора) iL , вероятно, между 100≤iLi3≤200 – то есть базовый ток, вероятно, будет составлять от 0,5% до 1% тока нашего светодиода.

Это очень грубое предположение плюс знание того, что желаемый ток нагрузки светодиода составляет iL=20 мА. , объедините, чтобы мы могли поставить максимум на i3 :

i3≤iL100i3≤20 мА100i3≤200 мкА

Максимальное ограничение значений сопротивления:

i3(R1//R2)≤85 мВ(R1//R2)≤85 мВ200 мкА(R1//R2)≤425 Ом

Теперь мы знаем, что хотим, чтобы параллельное сопротивление R1 и R2 не превышало 425 Ом. .

Мы снова используем другую аппроксимацию (примечание: добавление большей ошибки, выходящей за наши прежние границы!) И помните, что если два резистора имеют очень разные номиналы, мы можем аппроксимировать их параллельное сопротивление как просто меньшее сопротивление.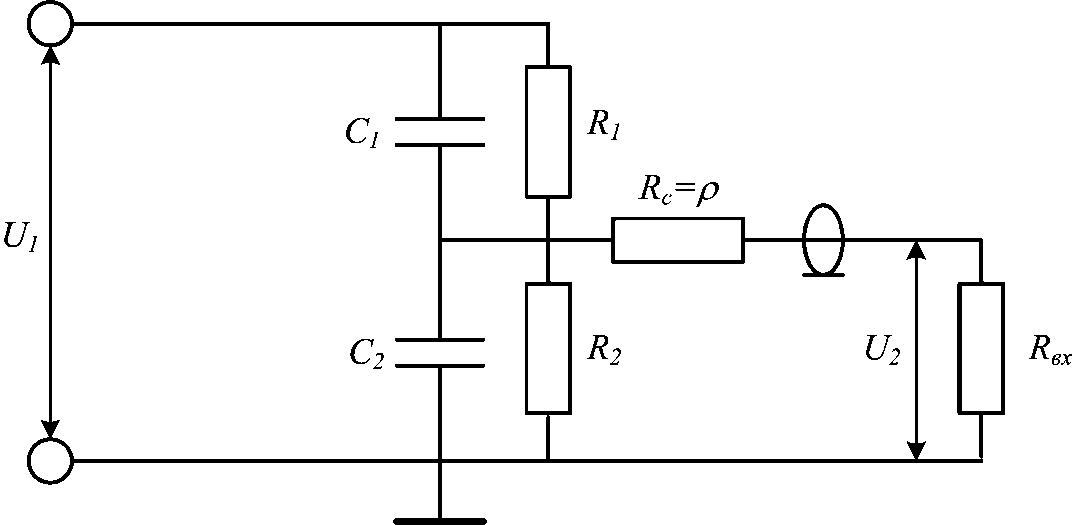 Наш коэффициент R2R1=0,52 недостаточно велик, чтобы это было правдой, но достаточно хорош для решения «обратной стороны конверта» и позволяет нам быстро выбрать некоторые общие номиналы резисторов, зная, что мы ищем соотношение примерно два к одному. где меньшее значение находится примерно в 400 Ом стадион:

R1=910 Ом R2=470 Ом

Это дешевые и распространенные номиналы резисторов, и мы получаем:

(R1//R2)=R1R2R1+R2=310 ОмR2R1=0,516

Это соответствует нашему ограничению погрешности напряжения и почти точно соответствует желаемому соотношению.Это достаточно близко, чтобы другие допуски (например, для отдельных резисторов и транзисторов) доминировали над общей ошибкой.

Вот наша окончательная схема управления током светодиода с резисторами R1 и R2:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Запустите симуляцию постоянного тока и посмотрите, как ток светодиода регулируется, чтобы он составлял около 20 мА.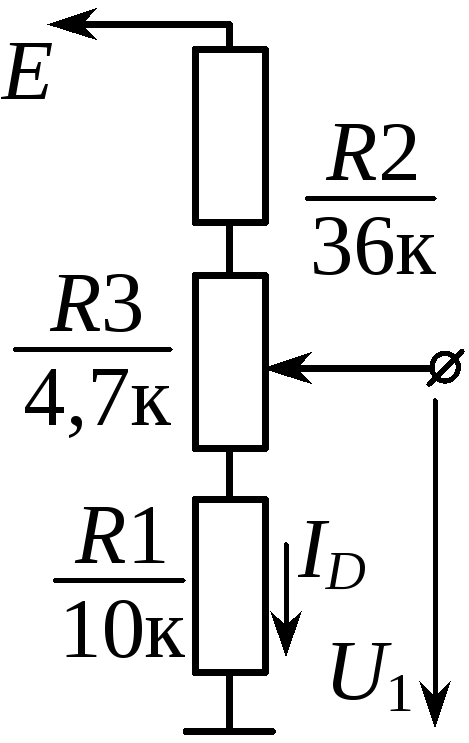 Вы также увидите расчетную мощность рассеивания на резисторах делителя напряжения P(R1)+P(R2). .

Насколько чувствительна эта схема к выбранным значениям резисторов R1 и R2? Что, если мы сохраним отношение f=R2R1=0.52 , но выбрать разные (оба большие или оба меньшие) номиналы резисторов? Режим DC Sweep симулятора позволяет нам быстро ответить на этот вопрос. Сначала мы определяем свободную переменную параметра x , а затем позвольте двум сопротивлениям масштабироваться вместе с ним:

R1=xR2=0,52x

Вот симуляция, показывающая ток светодиода при различных значениях x. :

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Запустите DC Sweep по параметру x и посмотрите, как изменяется ток светодиода, когда мы регулируем сопротивления на много порядков.

Обратите внимание, что точка, которую мы выбрали выше, x=910 , находится прямо перед «коленом» — визуально почти кусочно-линейным изменением поведения на кривой — где производительность начинает быстро ухудшаться. Мы построили график с использованием логарифмической шкалы для параметра, чтобы вы могли увидеть эффект замены сопротивлений на многие порядки величины. Прокрутите вниз, чтобы увидеть график рассеивания тепла резистором, так как это то, что мы обычно хотели бы минимизировать. Симуляторы цепей позволяют быстро увидеть этот эффект «колена», а не вычислять его по множеству точек.

Выбирая точку немного ближе к устойчивой стороне колена, мы получаем желаемое последовательное поведение при минимальном потреблении энергии.

---

Мы можем использовать симулятор, чтобы посмотреть, правильно ли работает схема, если разные значения компонентов различаются. Мы могли бы ожидать отклонения в светодиоде, в транзисторе и во всех номиналах резисторов. Мы также можем ожидать некоторую разницу в напряжении питания.

В каждом случае мы можем использовать режим моделирования DC Sweep для изменения компонента.

Вот что происходит, когда транзистор сильнее или слабее:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Ток светодиода не сильно зависит от производительности транзистора.

А вот что происходит, когда светодиод немного отличается:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Ток светодиода также не сильно зависит от параметров светодиода — мы разработали хороший регулятор тока!

Мы также можем использовать DC Sweep для изменения двух разных параметров.Например, предположим, что и R1, и R2 имеют диапазоны допуска 5%:

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Ток светодиода отображается для различных комбинаций значений резисторов R1 и R2.

В этом случае мы видим примерно +/- 10% общего диапазона токов светодиодов, что соответствует совокупным ошибкам наших двух отдельных допусков +/- 5%.

В производстве мы хотели бы проверить все наши технологические углы — все наши крайние допуски для всех наших компонентов — чтобы убедиться, что схема по-прежнему работает достаточно хорошо.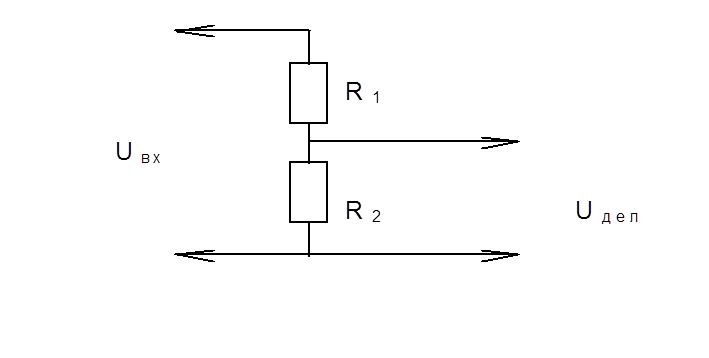 Если это не так, нам придется перепроектировать или уточнить схему, используя компоненты с более жесткими допусками, что может увеличить стоимость.

Если у вас есть N параметры компонента с диапазонами допусков, которые теоретически могут составлять 2N углы проверить! На практике мы используем нашу инженерную интуицию для поиска наиболее потенциально проблемных из них, и мы разрабатываем наши схемы так, чтобы они были надежными по своей конструкции, как описано выше.

---

Одним из распространенных вариантов использования делителя напряжения является измерение неизвестного значения сопротивления.Например, мы можем использовать фиксированное значение сопротивления R1 и неизвестное значение R2, которое мы хотели бы определить. (Например, R2 может быть резистором, зависящим от температуры или света.)

В этом случае мы можем измерить выходное напряжение делителя напряжения vout (например, с помощью мультиметра или аналого-цифрового преобразователя) и выразить это как долю известного приложенного напряжения vin .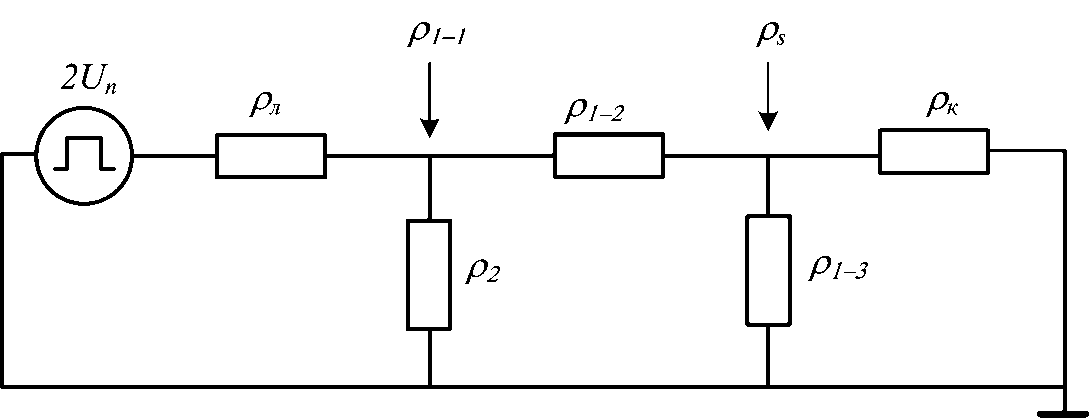 Тогда мы решим уравнение идеального делителя напряжения для неизвестного сопротивления следующим образом:

voutvin=f=R2R1+R2fR1+fR2=R2fR1=(1−f)R2R2=R1(f1−f)

Если мы знаем R1 , и мы можем измерить f , затем вычисляя R2 прост.

Упражнение Нажмите, чтобы открыть и смоделировать приведенную выше схему. Развертка постоянного тока варьирует R2. График настроен так, чтобы показать отношение f на верхнем графике, а затем использует приведенное выше уравнение для обратного расчета значения R2 от измеренных напряжений.

---

Вернитесь к оглавлению, чтобы продолжить. Скоро появятся новые разделы!

---

Роббинс, Майкл Ф. Абсолютная электроника: проектирование и анализ практических схем. CircuitLab, Inc., 2021, Ultimateelectronicsbook.ком. Доступ . (Авторское право © 2021 CircuitLab, Inc.)

Как разделять и властвовать над разделителем: Pr

Аннотация: В этой статье представлена ​​простая электронная таблица для проектирования резистивных делителей напряжения с использованием стандартных номиналов резисторов 1%. В примечаниях к применению описывается, как использовать электронную таблицу, и приводится ссылка для загрузки файла электронной таблицы.

Резистивный делитель напряжения — это базовая схема, которую изучают в каждом вводном курсе по электронике. Но выбрать значения из стандартных компонентов не так просто.Если вы когда-нибудь оказывались перед набором резисторов, вводя значения в свой калькулятор, то эта статья поможет вам.

Проблема заключается в том, что типичные комплекты резисторов не имеют всех номиналов. В этой статье демонстрируется небольшая электронная таблица, которая содержит таблицу номиналов резисторов с точностью до 1 % и позволяет легко найти необходимое соотношение, используя два доступных резистора.

Стандартные значения резисторов 1 % логарифмически разнесены на каждую 1/96-ю часть десятилетия. На рис. 1 показана табличная таблица со значениями резисторов 1 %, округленными до трех значащих цифр.((B$4+$A5)/96), который копируется в B5 через G20. Значения, выделенные желтым цветом, обычно доступны в наборах резисторов. Эти желтые блики с первого взгляда говорят вам, что типичный комплект содержит чуть больше четверти значений.

Рис. 1. Эта таблица не только содержит список номиналов резисторов с точностью до 1 %, но также позволяет легко определить отношение резисторов к делителям, используя два общедоступных значения (выделенные желтым цветом ячейки) из типичного набора резисторов.

На рис. 2 показано типичное применение резистивного делителя: внешняя обратная связь для регулятора напряжения, такого как понижающий преобразователь MAX8560 4 МГц.Соотношение делителя R2/(R1+R2) устанавливает выходное напряжение регулятора. MAX8560 имеет порог обратной связи 0,6 В на FB. В этом примере требуется выходное напряжение 1,5 В.

Рис. 2. Соотношение резистор-делитель R2/(R1+R2) задает выходное напряжение понижающего стабилизатора MAX8560 4 МГц. Электронная таблица на рис. 1 упрощает выбор R1 и R2 из общедоступных значений.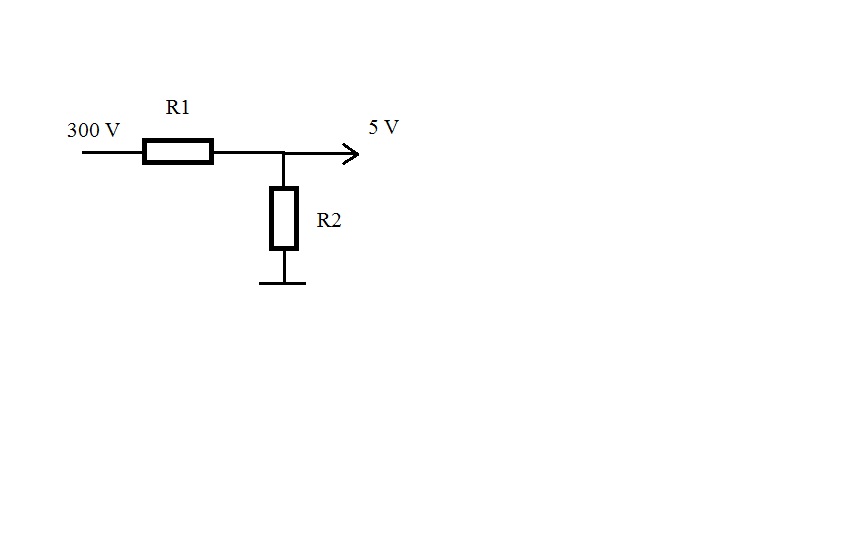

Чтобы рассчитать значения R1 и R2, введите требуемое выходное напряжение регулятора (напряжение на вершине делителя) в ячейку B3 и порог обратной связи регулятора (напряжение на средней точке делителя) в ячейку C3.Затем формула электронной таблицы в ячейке D3 имеет вид =96*LOG(B3/C3-1), что возвращает значение +16,9 шага для этого примера. Этот результат представляет собой количество шагов резистора с шагом 1 %, которые отделяют резисторы R1 от R2. Следовательно, если вы используете R2 = 100 кОм (ячейка B5), вы переместитесь на +17 шагов вниз по списку до R1 = 150 кОм (ячейка C6). Это был бы хороший выбор, поскольку оба резистора выделены желтым цветом (т. е. общедоступны).

Из электронной таблицы очень быстро видно, что R2 = 110 кОм не является хорошим выбором для этого примера, поскольку R1 = 165 кОм обычно не используется.Вы можете так же быстро определить исчерпывающий список общедоступных номиналов резисторов, которые подойдут: 1,00:1,50, 1,21:1,82, 1,62:2,43, 1,82:2,74, 2,00:3,01, 2,21:3,32, 3,32:4,99 и 4,99: 7. 50.

Когда количество шагов D3 отрицательное, R1 меньше R2 и вы перемещаетесь в противоположном направлении по списку значений. В любом направлении вы можете прокрутить список от 9,76 до 1,00, указывая на то, что вы перешли к следующему десятилетию резисторов.

Электронная таблица, показанная на рис. 1, доступна для загрузки в формате Microsoft Excel на сайте Resistor Values.Он также доступен в формате Pocket Excel для Pocket PC по адресу Pocket Resistor Values. Он отформатирован, чтобы соответствовать экрану Pocket PC. Если вы используете резистивные делители для целей, отличных от обратной связи регулятора, вы можете переименовать ячейки B2 и C2 в «Vtop» и «Vmid» соответственно.

© , Максим Интегрейтед Продактс, Инк.

Содержание этой веб-страницы защищено законами об авторском праве США и других стран. Для запросов на копирование этого контента, свяжитесь с нами.

ПРИЛОЖЕНИЕ 3646: ПРИМЕЧАНИЕ ПО ПРИМЕНЕНИЮ 3646, АН3646, АН 3646, APP3646, приложение3646, Приложение 3646

maxim_web:en/products/sensors-and-sensor-interface,maxim_web:en/products/analog/amps,maxim_web:en/products/power/supervisors-voltage-monitors-sequencers

maxim_web:en/products/sensors-and-sensor-interface,maxim_web:en/products/analog/amps,maxim_web:en/products/power/supervisors-voltage-monitors-sequencers

Базовое руководство по делителям напряжения

В этом руководстве мы рассмотрим очень важный и фундаментальный элемент электронных схем — делители напряжения.

Делитель напряжения представляет собой простейшую пассивную схему, играющую очень важную роль. Проще говоря, делитель напряжения преобразует большое напряжение в меньшее.

Базовая схема делителя напряжения состоит из двух последовательно соединенных резисторов, которые создают выходное напряжение, которое составляет лишь часть его входного напряжения.

Входное напряжение подается на два резистора, а желаемое выходное напряжение поступает от соединения между двумя резисторами.Второй резистор обычно подключается к земле.

Базовая схема делителя напряжения

Ниже приведены несколько примеров того, как вы можете увидеть настройку или схему схемы делителя напряжения.

Все схемы делителя напряжения должны выглядеть примерно одинаково. Цепи должны состоять из двух резисторов. Один резистор должен быть подключен к земле, другой к источнику напряжения и проводу, идущему между парой с выходным напряжением.

Как вы можете видеть в базовой настройке схемы делителя напряжения резистор, ближайший к входному напряжению ( Vin ), обычно обозначается как R1. Ближайший к заземлению резистор обычно обозначается как R2 .

Падение напряжения, вызванное входным напряжением, проходящим через пару резисторов ( R1 и R2 ), обозначается как Vout .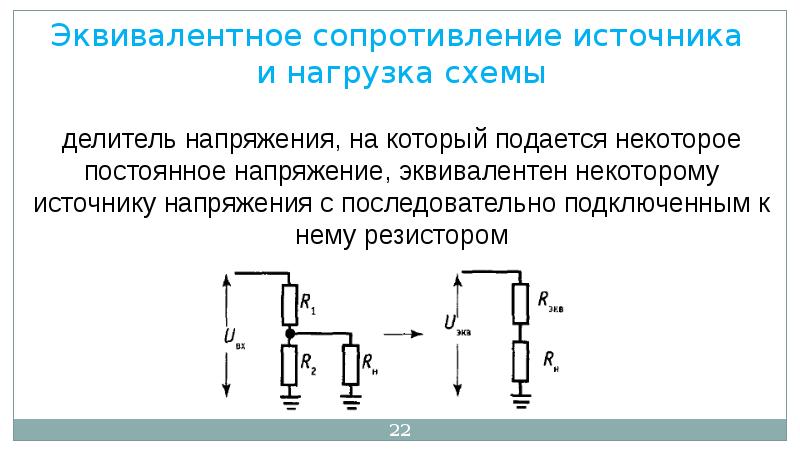

Результирующее падение напряжения — это то, что мы будем называть нашим разделенным напряжением. Это разделенное напряжение является частью исходного входного напряжения ( Vin ).

Мы используем R1 , R2 , Vin и Vout для обозначения элементов схемы, поскольку они имеют решающее значение для понимания значений, которые вам понадобятся для уравнения делителя напряжения.

Формула делителя напряжения

Уравнение делителя напряжения предполагает, что вы знаете три значения, используемые в схеме.

Чтобы воспользоваться уравнением, вам необходимо знать следующие три значения.

Вам необходимо знать номиналы резисторов ( R1 и R2 ), а также входное напряжение ( Vin ).

Использование этих трех значений в приведенном ниже уравнении позволит нам рассчитать выходное напряжение схемы делителя напряжения.

Теперь мы в последний раз пройдемся по переменным, используемым в уравнении делителя напряжения, чтобы у вас было четкое представление о каждой переменной.

• VIN — это входное напряжение, измеренное в вольтах ( V )
• R1 — устойчивость к устойчивости 1-го резистора в разделите напряжения, измеренные в Ом Ом
• R2 2-й резистор в делителе напряжения, измеряется в Ом Ω
• Vвых выходное напряжение измеряется в вольтах ( В )

Делитель напряжения Калькулятор Если вы хотите быстро рассчитать выходное напряжение генерируемого вашей схемой делителя напряжения, вы можете воспользоваться нашим удобным калькулятором.

Все, что вам нужно сделать, это ввести значения для ваших двух резисторов и входного напряжения, калькулятор автоматически вычислит соответствующее выходное напряжение.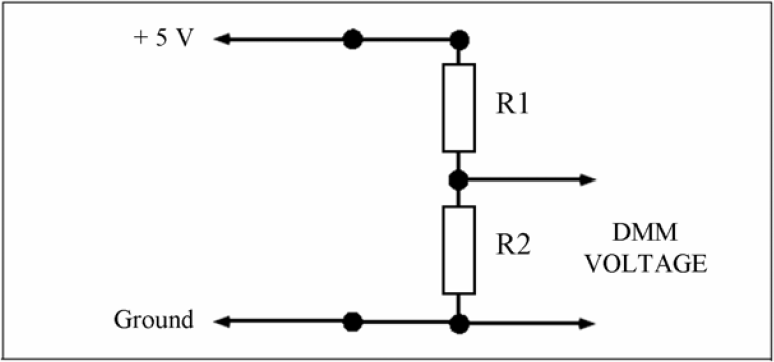

Разделитель напряжения Формула Примеры формулы

Для нашего первого примера использовании формулы делителя напряжения мы собираемся использовать следующие значения:

• VIN AS 5 V,
• R1 AS 220 Ω резистор,
• и R2 как резистор 680 Ом.

Теперь, если мы подставим эти значения в наше уравнение делителя напряжения, мы должны получить что-то вроде того, что показано ниже.

Для начала мы сначала сложим значения резисторов R1 и R2 вместе. Таким образом, в нашем примере выше это будет 220 + 680 , что равно 900 .

Мы заменим 220 + 680 в нашей формуле нашим результатом, так что мы получим следующее уравнение.

Теперь, когда мы сделали простое сложение, мы можем наконец вычислить часть деления уравнения делителя напряжения.

Просто разделите значение R2 на рассчитанное значение R1 + R2 . В нашем примере это будет 680 , разделенное на 900 .

С помощью калькулятора это даст нам 0,7555555555555556 , но для простоты мы округлим это число до 2 знаков после запятой, то есть число станет 0.76 .

Замените часть вашей формулы на полученное вами значение. Теперь ваше уравнение должно выглядеть так, как показано ниже.

Наконец, мы можем просто умножить Vin на нашу рассчитанную величину деления резистора. В нашем случае просто умножьте 5 на 0,76 .

Результат этого умножения даст вам сумму Vout . В нашем случае этот результат был 3,8 Вольт.

Упрощение формулы

Есть несколько упрощений, которые мы можем внести в уравнение делителя напряжения.Однако в этом руководстве мы проведем вас только через приведенное ниже.

Используя упрощения, вы можете упростить быструю оценку схемы делителя напряжения.

Это упрощение говорит о том, что если номиналы резистора R1 и резистора R2 одинаковы, то выходное напряжение равно половине входного напряжения.

Применение делителя напряжения

Делители напряжения имеют множество применений в электронных схемах и являются основным компонентом многих электронных схем.

Ниже мы покажем вам некоторые из немногих применений схемы делителя напряжения.

Потенциометры

Потенциометр является одним из наиболее часто используемых элементов электронных схем и используется в качестве основного компонента в большом количестве различных продуктов.

Некоторые примеры устройств, в которых используется потенциометр:

• Измерение положения на джойстике
• Создание опорного напряжения
• Контроль уровня звука в динамиках
• Среди прочего

Потенциометр представляет собой переменный резистор, который действует точно так же, как регулируемые делители напряжения.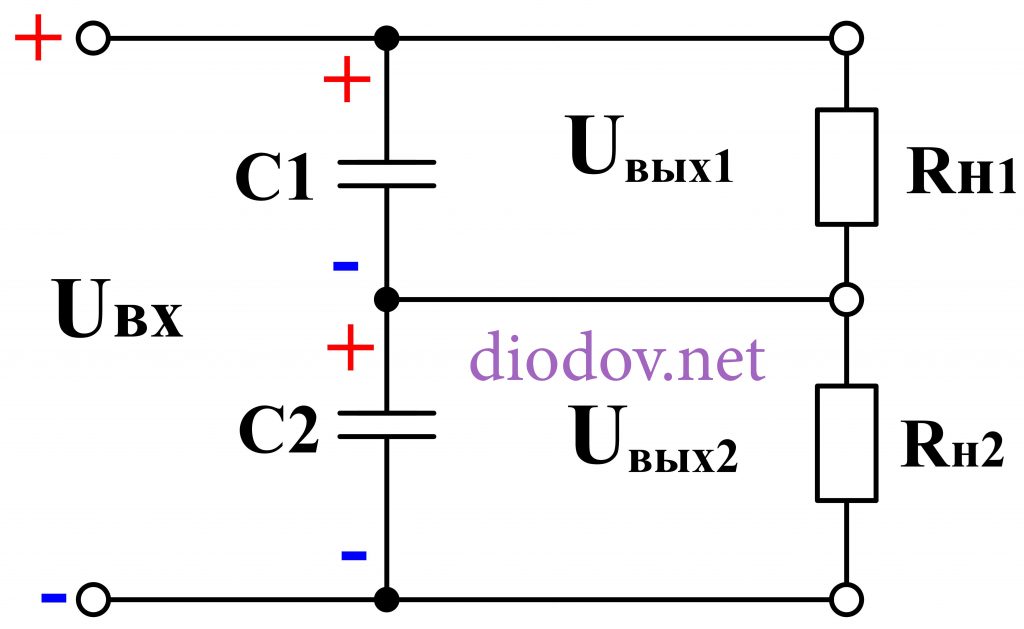

Внутри потенциометра находится один резистор, разделенный грязесъемником. Этот дворник — это то, что вы перемещаете, что регулирует соотношение между двумя половинами резистора.

Снаружи горшка вы найдете три контакта, контакты с обеих сторон являются соединением между каждым концом резистора, вы можете рассматривать их как R1 и R2 .

Штифт посередине — это то, что подключено к дворнику. Теоретически это похоже на Vout в схеме делителя напряжения.

Чтобы подключить потенциометр, чтобы он работал как регулируемый делитель напряжения, вам нужно будет подключить одну сторону к вашему входному напряжению ( Vin ), а другую сторону к вашей земле.

При правильном подключении обоих внешних контактов средний контакт будет действовать как выход делителя напряжения ( Vout ).

Поворот потенциометра в одну сторону приведет к тому, что напряжение будет приближаться к нулю, а в другую сторону — к входному напряжению.

Поворот потенциометра в среднее положение означает, что выходное напряжение будет вдвое меньше входного.

Сдвиг уровня

Сдвиг уровня — важная концепция, которую необходимо понимать при работе с цифровой электроникой. Их также можно назвать схемой «переключателя логического уровня» или «перевода уровня напряжения».

Переключатели уровня используются для переключения напряжения с одного уровня на другой. Это часто используется для обеспечения совместимости между ИС, которые имеют разные требования к напряжению.

Некоторые из более сложных датчиков, которые используют такие интерфейсы, как UART, SPI или I2C для передачи своих показаний, часто работают с разными уровнями напряжения.

Одним из примеров потенциального использования этого является работа с платой микроконтроллера, такой как Raspberry Pi.

Raspberry Pi — интересный пример удобного переключателя уровней. Несмотря на то, что Raspberry Pi обеспечивает выходную мощность как 5 В, так и 3,3 В, его контакты GPIO рассчитаны только на входное напряжение 3,3 В.

Использование делителя напряжения в цепи позволит нам понизить напряжение с 5 В до 3,3 В для входного контакта.

Ниже мы рассмотрим пример использования схемы делителя напряжения с Raspberry Pi для смещения уровня выходного сигнала датчика с 5 В до 3,3 В.

Пример сдвига уровня

Например, в нашем руководстве по датчику расстояния мы используем ультразвуковой датчик HC-SR04.

Этот датчик использует входное питание 5 В, что означает, что нам нужно понизить выход на выводе Echo с 5 В до 3.3 В, прежде чем он достигнет контактов GPIO.

Мы можем рассчитать нужные нам резисторы, выбрав начальное значение резистора. Резисторы между 1 кОм – 10 кОм лучше всего подходят для снижения напряжения с 5 В до 3,3 В .

В нашем примере мы будем использовать резистор 1 кОм . Чтобы вычислить второй резистор, который нам нужно использовать, мы будем использовать еще одну переработанную версию уравнения делителя напряжения.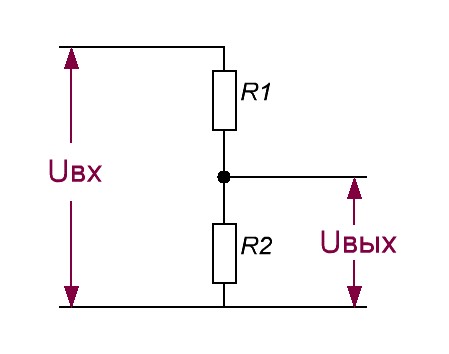

Чтобы рассчитать значение R2, нам нужно знать Vin , Vout и значение нашего резистора R1, который мы планируем использовать.

Имея под рукой эти 3 значения, мы можем использовать следующее уравнение.

Заполнив это уравнение нашими известными значениями, мы можем использовать его для расчета номинала резистора, необходимого для снижения напряжения с 5 В до 3,3 В.

С нашими входными и выходными значениями и нашим резистором R1 1 кОм вы должны получить следующее уравнение.

Сначала нужно вычислить обе половины деления, если умножить на Vout ( 3.3 ) на значение R1 ( 1000 ) должно получиться 3300 .

Теперь нам также нужно сделать нижнюю половину, вычитая Vout из Vin , в этом примере это 5 – 3. 3 что равно 1.7 .

Наконец, разделите оба значения, чтобы получить значение сопротивления, в нашем примере это 3300 , деленное на 1,7 .

Введя это в калькулятор, мы получим большое длинное число, но мы упростим его до ближайших 2 десятичных знаков.

С этим значением мы можем сделать вывод, что резистора 2 кОм должно быть более чем достаточно, чтобы понизить напряжение 5 В до 3,3 В .

Чтение Резистивные датчики

Вы можете заметить, что многие датчики в реальном мире представляют собой простые резистивные устройства, предназначенные для реагирования на определенные элементы.

Например, датчик LDR (Light Dependent Resistor), подобный тому, который мы используем в нашем руководстве по датчику света, работает, создавая сопротивление, пропорциональное количеству подобного, которое касается его.

Существует также множество других датчиков, которые фактически представляют собой просто причудливые резисторы, такие как термисторы, датчики изгиба и чувствительные к силе резисторы.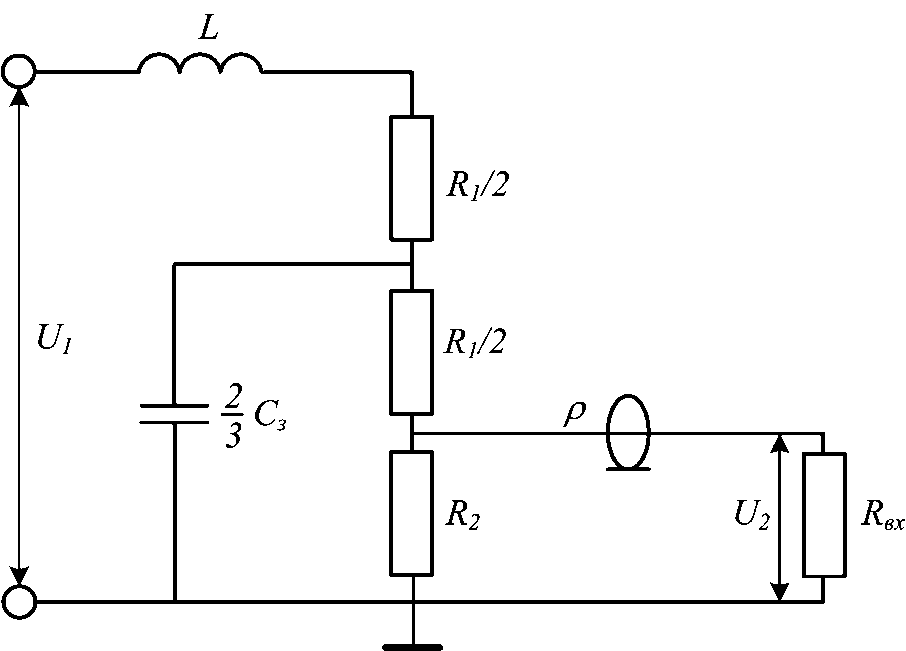

К сожалению, в отличие от напряжения (в сочетании с аналого-цифровым преобразователем), сопротивление не так просто измерить для таких компьютеров, как Raspberry Pi.

Однако мы можем упростить задачу, переделав схему в делитель напряжения. Это просто, как добавление резистора, поэтому схема намного больше похожа на схемы, которые мы показывали ранее в этом руководстве.

Таким образом, мы можем использовать напряжение, полученное от делителя напряжения, для расчета текущего уровня освещенности.

Добавив резистор известного вам значения, например, резистор 1 кОм, вы сможете рассчитать сопротивление фоторезистора при различных уровнях освещенности, перестроив использованное ранее уравнение.

Все, что нам нужно знать, это Vin , Vout и номинал резистора R1 .

Используя приведенное выше уравнение, вы можете быстро рассчитать сопротивление LDR при самом темном и самом ярком уровне освещенности.

Это дало бы нам представление о самом высоком и самом низком сопротивлении.

Когда у вас есть оба этих значения сопротивления, вы можете вычислить значение резистора, которое находится между ними, это даст вам самое большое разрешение для расчета текущего света через аналого-цифровой преобразователь.

Например, сопротивление фотоэлемента может варьироваться от 1 кОм на свету до примерно 10 кОм в темноте.

Таким образом, используя резистор, номинал которого находится где-то посередине, например, 5.Резистор 1 кОм , мы можем получить самый широкий диапазон из нашего LDR.

Я надеюсь, что это руководство помогло вам понять, что такое делитель напряжения и как вы можете использовать его в схеме, а также рассчитать результирующее напряжение.

Если вы считаете, что мы что-то упустили или ошиблись, обязательно сообщите нам об этом в разделе комментариев ниже. Мы также открыты для любых других ваших отзывов.

Калькулятор делителя мощности Wilkinson – всё RF

Введите волновое сопротивление системы и отношение требуемой мощности на выходе, чтобы рассчитать полное сопротивление различных линий передачи, составляющих делитель мощности Уилкинсона.Пример: Коэффициент мощности будет равен 1 для делителя с одинаковыми выходами на обоих портах.

Введите конфигурацию импеданса и мощности делителя

Щелкните здесь для просмотра изображения

Что такое делитель мощности Wilkinson?

Делитель мощности Wilkinson использует четвертьволновые трансформаторы для разделения входного сигнала на два выходных сигнала с одинаковой фазой. Он также обеспечивает изоляцию между выходными портами при сохранении согласованного состояния на всех портах. Применяется в области СВЧ-техники.

Делитель мощности Wilkinson имеет три порта (показан ниже на рис.). Делитель мощности Уилкинсона разделяет входной сигнал от порта 1 на два выходных сигнала с одинаковой фазой (порт 2 и порт 3).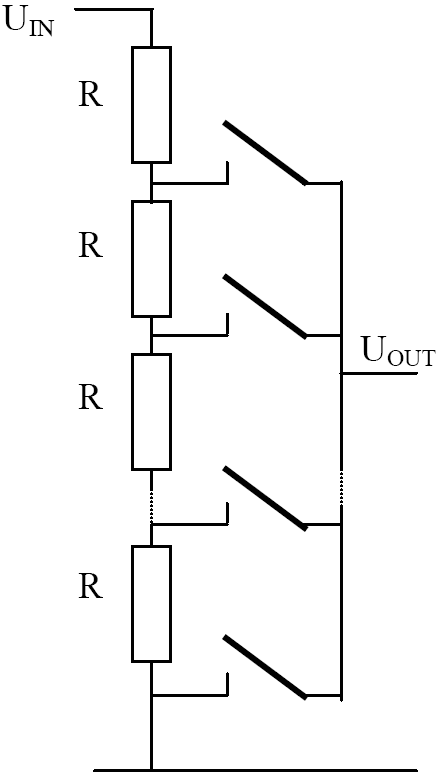 Он обеспечивает изоляцию между выходными портами при сохранении согласованного состояния на всех портах.

Также он может работать в обоих направлениях, т.е. может использоваться и как сумматор мощности для объединения сигналов, поступающих на порты 2 и 3, в один (выйдет на порт 1).

Идеальный двухпортовый делитель мощности Уилкинсона

Конструкция двустороннего делителя мощности Уилкинсона включает входную ветвь с волновым сопротивлением (Zo), два четвертьволновых трансформатора с полным сопротивлением 1.414 x Zo и резистор (R) между портами 2 и 3 для обеспечения согласования импедансов, а также изоляции между выходными портами (2 и 3).

Когда сигнал поступает на входной порт 1, он разделяется на два сигнала с одинаковой амплитудой и одинаковой фазой и появляется как выход на портах 2 и 3. Поскольку резистор (R) между портами 2 и 3 равен тот же потенциал, ток через резистор отсутствует; следовательно, резистор отделен от входа.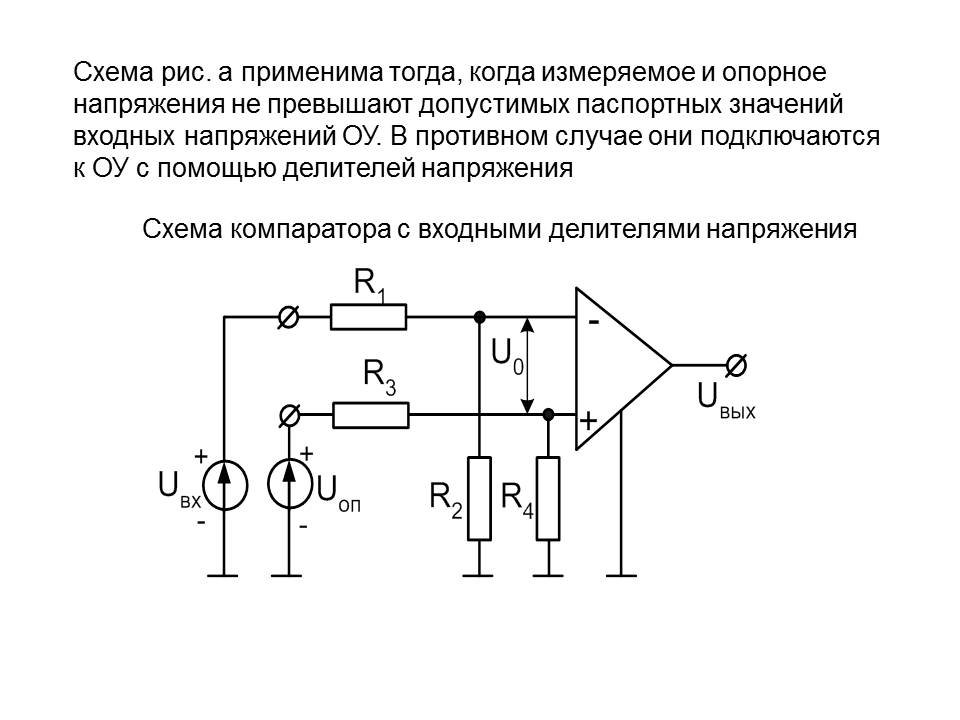

Изменяя номинал резистора (R), можно изменять величину разделения мощности между портами 2 и 3.Соотношение между R, Zo и количеством деления мощности определяется следующей формулой.

R = Zo (K + 1/K)

Где, K2 = P3 / P2; (P3 — питание на порту 3) (P2 — питание на порте 2).

Где,

P _A = выходная мощность порта 2

P _B = выходная мощность порта 3

Z ₀ = характеристическое полное сопротивление всей системы 9009 9008 R

5

5 между двумя выходными портами.

Z ₁ , Z ₂ , Z ₃ , Z ₄ = импедансы ветвей

Равномерный делитель Уилкинсона с равным разделением получается при K=1.

Загрузите приложение RF Calculator

Загрузите приложение RF Calculator на устройства Android или iOS.