Последовательное соединение резисторов расчет — Moy-Instrument.Ru

Последовательное и параллельное соединение резисторов

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

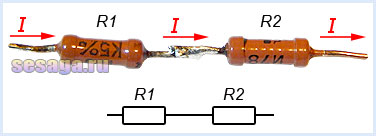
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора

R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

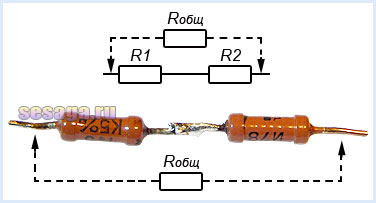
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное

соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

Последовательное соединение резисторов. Схема соединения и примеры расчета

Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.

Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.

Последовательное соединение резисторов

На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.

Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:

То есть, в нашем случае общее сопротивление цепи будет равно:

R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм

Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.

Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.

Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).

Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:

Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:

В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.

В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:

Пример № 1

Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:

Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:

Пример № 2

Необходимо рассчитать падение напряжения на выводах «А» и «В»:

а) без подключенного резистора R3

б) с подключенным резистором R3

Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.

Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).

Расчет сопротивления параллельного соединения резисторов

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Соединение резисторов

Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.

Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!

Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.

Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.

Последовательное соединение резисторов.

В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ

Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.

Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как R_общ.

Номинальные сопротивления резисторов включённых в цепь обозначаются как R₁, R₂, R₃,…R_N.

Применяя последовательное соединение, стоит помнить одно простое правило:

Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.

Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.

Параллельное соединение резисторов.

Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно

Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.

Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R₁ – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.

Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте тут.

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Соединение резисторов

Соединение резисторов разными способами позволяет получить необходимую величину сопротивления и мощности рассеивания одного эквивалентного резистора. Всего существует три способы соединения резисторов – последовательное, параллельное и смешанное.

Последовательное соединение резисторов

Последовательное соединение резисторов предполагает использование двух и более радиоэлектронных элемента. Конец предыдущего элемента соединяется с началом последующего и так далее. При последовательном соединении сопротивления и мощности рассеивания всех резисторов складываются.
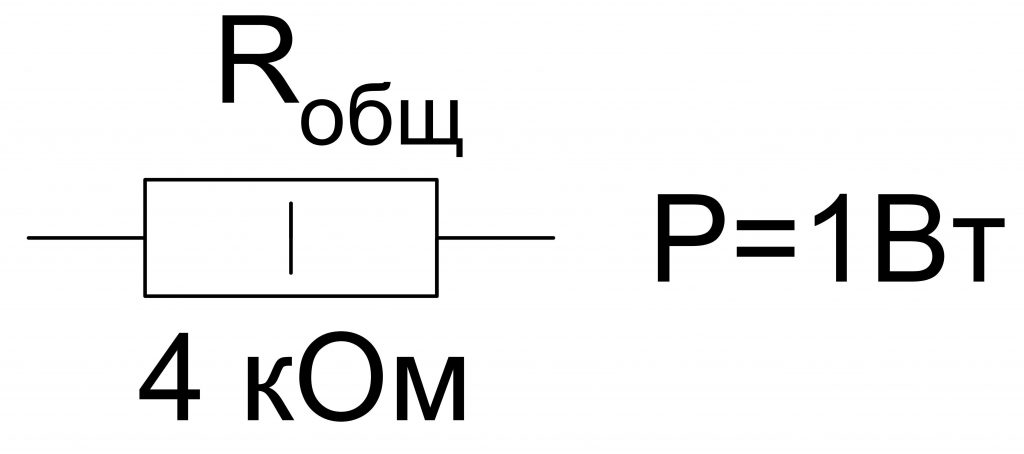
Рассмотрим следующий пример. Соединим последовательно четыре резистора, каждый имеет R = 1 кОм и мощность рассеивания P = 0,25 Вт.

Rобщ = R1 + R2 + R3 + R4 = 1кОм + 1кОм + 1кОм + 1кОм = 4 кОм.

Pобщ = P1 + P2 + P3 + P4 = 0,25 Вт + 0,25 Вт + 0,25 Вт + 0,25 Вт = 1 Вт.

Таким образом, получается один эквивалентный или общий резистор, имеющий следующие параметры:
Rобщ = 4 кОм; Pобщи = 1 Вт.

В последовательной цепи электрической ток протекает одной и той же величины, поэтому электроны на протяжении всего пути неизбежно наталкиваются на все препятствия в виде сопротивлений. С каждым препятствием уменьшается число свободных зарядов, что приводит к снижению силы электрического тока.

Параллельное соединение резисторов

При параллельном соединении резисторов увеличивается количество путей для перемещения свободных зарядов, то есть электронов, из одного участка пути к другому. Поэтому при параллельном соединении резисторов их суммарное (общее, эквивалентное) сопротивление всегда ниже наименьшего сопротивления из всех резисторов.

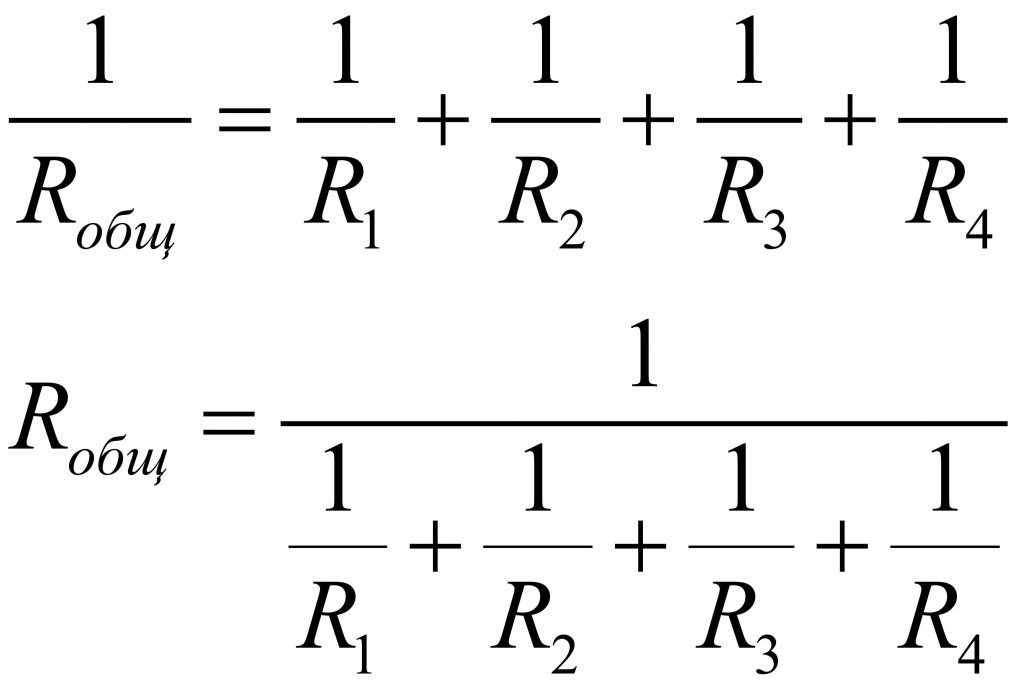
Величина, обратная сопротивлению называется проводимостью. Проводимость измеряется в сименсах [См] и обозначается большей латинской буквой G.

G = 1/R = 1/Ом = См

Поэтому при выполнении различных подсчетов в электрических цепях, имеющих параллельное соединение, пользуются проводимостью.

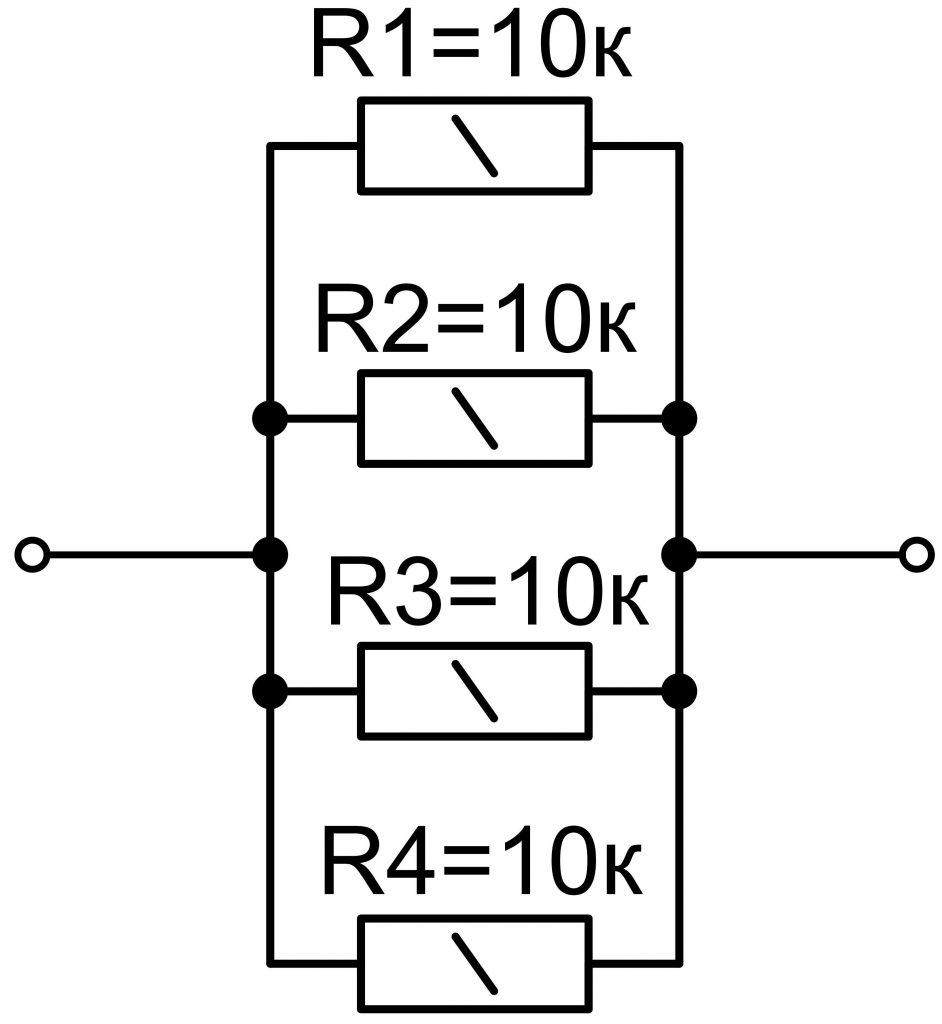
Если сопротивления всех параллельно соединенных резисторов равны, то для определения общего Rобщ достаточно R одного из них разделить на их общее количество:

Если R1 = R2 = R3 = R4 = R , то

Rобщ = R/4.

Например, каждый из четырех резисторов имеет R = 10 кОм, тогда

Rобщ = 10 кОм/4 = 2,5 кОм.

Мощности рассеивания суммируются также, как и при последовательном соединении.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой комбинации последовательных и параллельных соединений. В принципе любую даже самую сложную электрическую цепь, состоящую из источников питания, конденсаторов, диодов, транзисторов и других радиоэлектронных элементов в конкретный момент времени можно заменить резисторами и источниками напряжения, параметры которых изменяются с каждым последующим моментом времени. Для примера изобразим схему, имеющую несколько соединений.

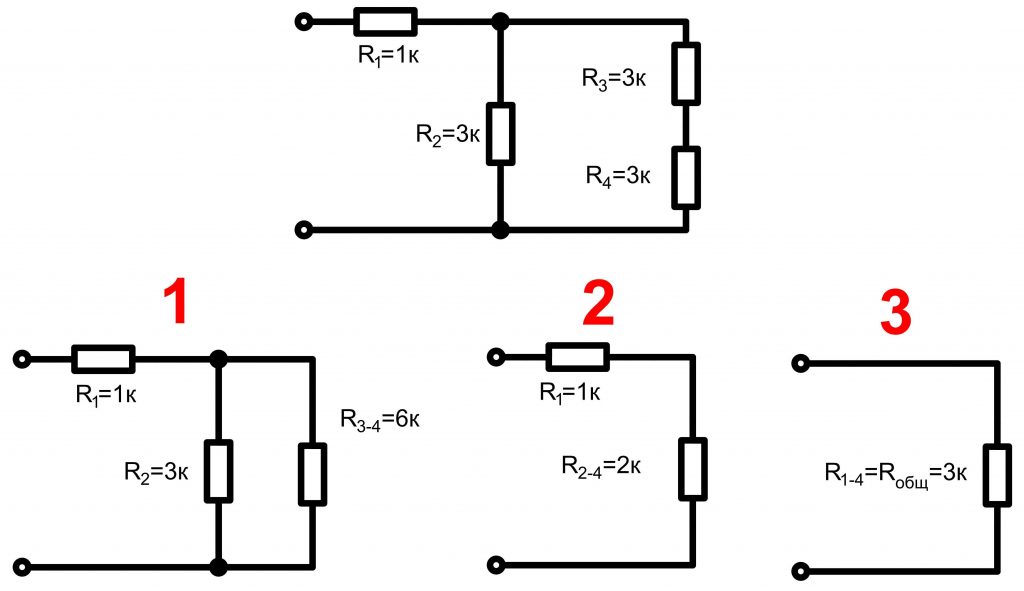
Общее (эквивалентное) сопротивление находится методом «сворачивания» схемы. Сначала определяется общее сопротивление одного отдельного соединения, затем последующего и так далее.

Теперь самостоятельно подсчитайте общее сопротивления схемы, приведенной ниже.

Последовательное и параллельное соединение резисторов

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

При включении трех резисторов расчет общего сопротивления будет таким:

Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

Резистор и сопротивление [База знаний]

Резистор и сопротивление

Теория

КОМПОНЕНТЫ

ARDUINO

ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ

---

Резистор — искусственное «препятствие» для тока. Сопротивление в чистом виде. Резистор ограничивает силу тока, переводя часть электроэнергии в тепло. Сегодня невозможно изготовить ни одно, сколько-нибудь функциональное, электронное устройство без резисторов. Они используются везде: от компьютеров до систем охраны.

Сопротивление резистора — его основная характеристика. Основной единицей электрического сопротивления является Ом. На практике используются также производные единицы — килоом (кОм), мегаом (МОм), гигаом (ГОм), которые связаны с основной единицей следующими соотношениями:

1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм

Ниже на рисунке видна маркировка резисторов на схемах:

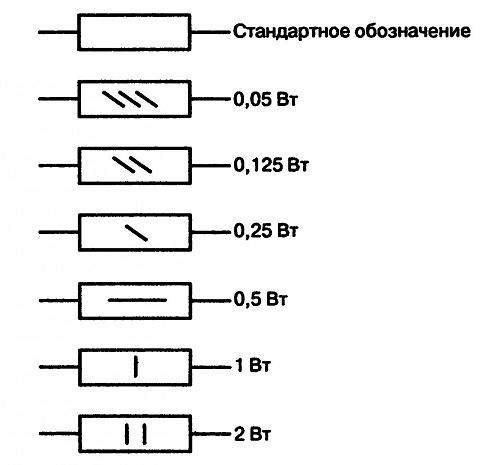
Наклонные линии обозначают мощность резистора до 1 Вт. Вертикальные линии и знаки V и X (римские цифры), указывают на мощность резистора в несколько Ватт, в соответствии со значением римской цифры.

 

Для соединения резисторов в схемах используются три разных способа подключения: параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.

 

---

Последовательное соединение резисторов

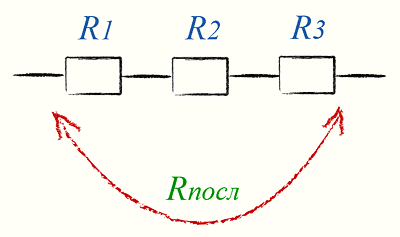Последовательное соединение резисторов применяется для увеличения сопротивления. Т.е. когда резисторы соединены последовательно, общее сопротивление равняется сумме сопротивлений каждого резистора. Например, если резисторы R1 и R2 соединены последовательно, их общее сопротивление высчитывается по формуле: R_общ = R₁ + R₂

Это справедливо и для большего количества соединённых последовательно резисторов:

R_общ = R₁ + R₂ + R₃ + … + R_n

Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.

При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.

Мощность при последовательном соединении

При соединении резисторов последовательно электрический ток по очереди проходит через каждое сопротивление. Значение тока в любой точке цепи будет одинаковым. Данный факт определяется с помощью закона Ома. Если сложить все сопротивления, приведенные на схеме, то получится следующий результат: R = 200 + 100 + 51 + 39 = 390 Ом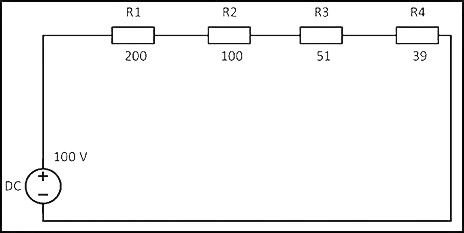

Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять

I = U/R = 100 В/390 Ом = 0,256 A

На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:

P = I² x R = 0,256² x 390 = 25,55 Вт

Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:

P₁ = I² x R₁ = 0,256² x 200 = 13,11 Вт;
P₂ = I² x R₂ = 0,256² x 100 = 6,55 Вт;
P₃ = I² x R₃ = 0,256² x 51 = 3,34 Вт;
P₄ = I² x R₄ = 0,256² x 39 = 2,55 Вт.

Если сложить полученные мощности, то общая Р составит:

Р_общ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт

 

---

Параллельное соединение резисторов

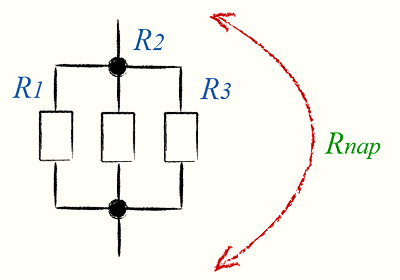Параллельное соединение резисторов необходимо для уменьшения общего сопротивления и, как вариант, для увеличения мощности нескольких резисторов по сравнению с одним.

Расчет параллельного сопротивления двух параллельно соединённых резисторов R₁ и R₂ производится по следующей формуле:

R_общ = (R₁ × R₂) / (R₁ + R₂)

Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:

1 / R_общ = 1 / R₁ + 1 / R₂ + … + 1 / R_n

Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.

Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.

Мощность при параллельном соединении

При параллельном подключении все начала резисторов соединяются с одним узлом схемы, а концы – с другим. В этом случае происходит разветвление тока, и он начинает протекать по каждому элементу. В соответствии с законом Ома, сила тока будет обратно пропорциональна всем подключенным сопротивлениям, а значение напряжения на всех резисторах будет одним и тем же. 1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом

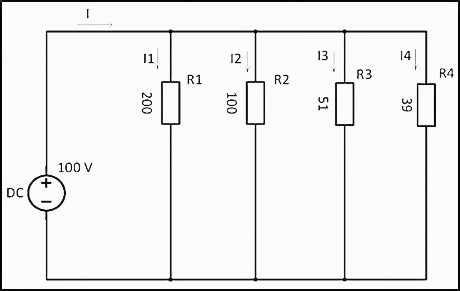
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока

I = U/R = 100 В x 0,06024 Ом = 6,024 A

Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом

P = I² x R = 6,024² x 16,6 = 602,3 Вт

Расчет силы тока для каждого резистора выполняется по формулам:

I₁ = U/R₁ = 100/200 = 0,5 A;
I₂ = U/R₂ = 100/100 = 1 A;
I₃ = U/R₃ = 100/51 = 1,96 A;
I₄ = U/R₄ = 100/39 = 2,56 A

На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.

Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:

P₁ = U²/R₁ = 100²/200 = 50 Вт;
P₂ = U²/R₂ = 100²/100 = 100 Вт;
P₃ = U²2/R₃ = 100²/51 = 195,9 Вт;
P₄ = U²2/R₄ = 100²/39 = 256,4 Вт

Если сложить полученные мощности, то общая Р составит:

Р_общ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт

 

---

Калькулятор

---

Цветовая маркировка резисторов

Наносить номинал резистора на корпус числами — дорого и непрактично: они получаются очень мелкими. Поэтому номинал и допуск кодируют цветными полосками. Разные серии резисторов содержат разное количество полос, но принцип расшифровки одинаков. Цвет корпуса резистора может быть бежевым, голубым, белым. Это не играет роли. Если не уверены в том, что правильно прочитали полосы, можете проверить себя с помощью мультиметра или калькулятора цветовой маркировки.

---

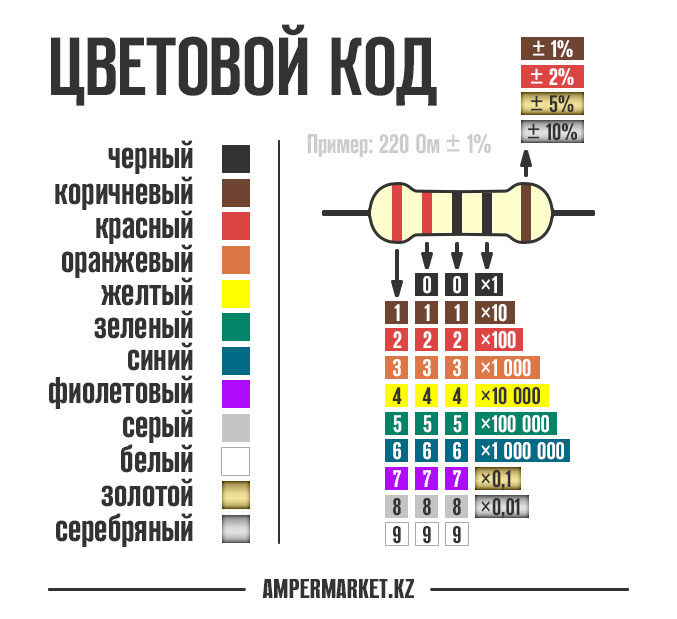
Калькулятор цветовой маркировки резисторов

---

Основные характеристики

Сопротивление (номинал)	R	Ом
Точность (допуск)	±	%
Мощность	P	Ватт

---

Переменный резистор

Переменный резистор — это резистор, у которого электрическое сопротивление между подвижным контактом и выводами резистивного элемента можно изменять механическим способом. Переменные резисторы (их также называют реостатами или потенциометрами) предназначены для постепенного регулирования силы тока и напряжения. Разница в том, что реостат регулирует силу тока в электрической цепи, а потенциометр — напряжение. Выглядят переменные резисторы так:

На радиосхемах переменные резисторы обозначаются прямоугольником с пририсованной к их корпусу стрелочкой.

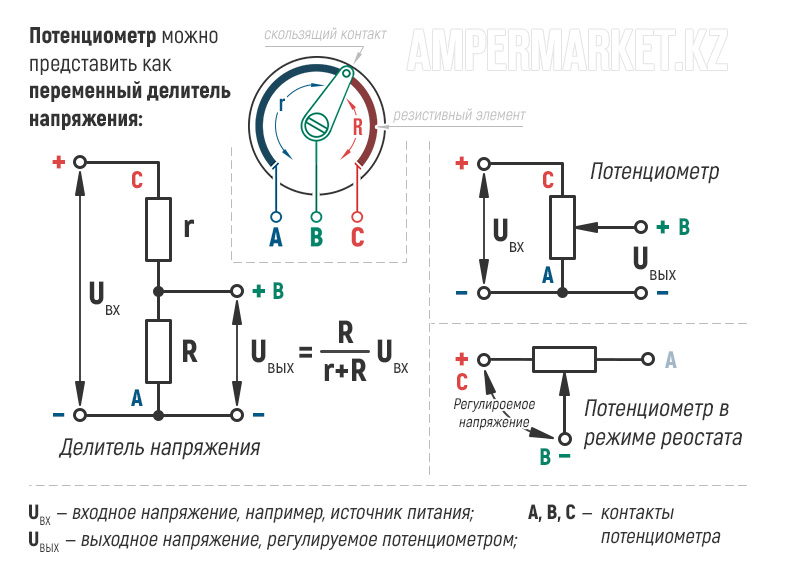
Регулировать величину сопротивления переменных резисторов можно с помощью вращения специальной ручки. Те из резисторов, у которых регулировка сопротивления резистора может осуществляться только с помощью отвертки или специального ключа-шестигранника, называются подстроечными переменными резисторами.

---

Термисторы, варисторы и фоторезисторы

Кроме реостатов и потенциометров есть и другие виды резисторов: термисторы, варисторы и фоторезисторы. Термисторы, в свою очередь, делятся на термисторы и позисторы. Позистор – это термистор, у которого сопротивление возрастает вместе с ростом температуры окружающей среды. У термисторов, наоборот, чем выше температура вокруг, тем меньше сопротивление. Это свойство обозначают как ТКС – тепловой коэффициент сопротивления.

В зависимости от ТКС (отрицательный он или положительный) обозначают на схеме термисторы следующим образом:

Следующий особый класс резисторов – это варисторы. Они изменяют силу сопротивления в зависимости от подаваемого на них напряжения. Зная свойства варистора, можно догадаться, что такой резистор защищает электрическую цепь от перенапряжения.

На схемах варисторы обозначаются так:

В зависимости от интенсивности освещения изменяет свое сопротивление еще один вид резисторов – фоторезисторы. Причем не важно, каков источник освещения: искусственный или естественный. Их особенность еще и в том, что ток в них протекает как в одном, так и в другом направлении, то есть еще говорят, что фоторезисторы не имеют p-n перехода.

А на схемах изображаются так:

---

Соединение резисторов — Основы электроники

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.

Рисунок 1. Соединение резисторов.

Последовательное соединение резисторов

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).

Рисунок 2. Последовательное соединение резисторов.

То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:

Rобщ = R1 + R2 + R3+…+ Rn.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).

Рисунок 3. Параллельное соединение резисторов.

При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:

1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn

Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:

Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.

Рисунок 4. Смешанное соединение резисторов.

На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.

Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.

Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Как отличается параллельное и последовательное соединение резисторов?

Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?

Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.

В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.

Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.

Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Теоретическая часть

Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Последовательное подключение.

Примеры расчета

Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.   R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2  А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором  — 1600 В.  При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Материал по теме: Как проверить варистор мультиметром.

Общее сопротивление R_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Параллельное подключение резисторов.

Общее сопротивление R_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

Схема параллельного соединения

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи. Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.

Формулы расчета параллельного и последовательного подключения.

Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.

Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк . Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой 1/R_эк = 1/R₁ + 1/R₂ + 1/R_3. Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G_3.

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи – R_эк=R₁R₂/(R₁+R₂) при трех параллельно включенных резисторах R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃).

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк = R1 / n.

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока: I1 = I / n. При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Более подробную информацию можно узнать, прочитав файл по данной теме “Расчет мощности резисторов”.  Всю новую информацию по этой и многим другим темам, вы сможете найти в группе. Подписывайтесь на нашу группу в социальной сети «Вконтакте».

Для этого вам необходимо будет перейти по следующей ссылке https://vk.com/electroinfonet. Также в группе можно задавать вопросы и получать на них подробные ответы от профи. В завершение объемной статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.elektroznatok.ru

www.themechanic.ru

www.electrono.ru

www.hightolow.ru

www.sxemotehnika.ru

Последовательное и параллельное соединение резисторов

Здравствуйте, уважаемые читатели сайта sesaga.ru. Очень часто в практике радиолюбителя при повторении или наладке радиоэлектронных устройств не всегда под рукой оказывается резистор с нужным сопротивлением, хотя резисторов с другими сопротивлениями имеются в достаточном количестве.

В такой ситуации поступают просто: берут несколько резисторов (два или три) с разными сопротивлениями и, соединяя их последовательно или параллельно, подбирают нужное сопротивление.

В этой статье Вы узнаете, как применяя то или иное соединение можно подобрать необходимое сопротивление.

Последовательное соединение резисторов.

Последовательным называют соединение, при котором резисторы следуют друг за другом и образуют электрическую цепь из нескольких элементов, в которой конец одного резистора соединен с началом другого и т.д.

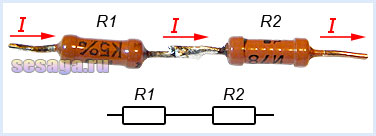
В последовательной цепи электрической ток поочередно протекает по всем резисторам и преодолевает сопротивление каждого из них. При этом ток в этой цепи одинаков. И если последовательно соединить два резистора R1 и R2, их общее (полное) сопротивление Rобщ будет равно сумме их сопротивлений. Это условие справедливо для любого числа резисторов, где:

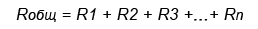
Например.
При соединении двух резисторов с номиналами R1 = 150 Ом и R2 = 330 Ом их общее сопротивление составит Rобщ = 150 + 330 = 480 Ом.

При соединении трех резисторов R1 = 20 кОм, R2 = 68 кОм и R3 = 180 кОм их общее сопротивление составит Rобщ = 20 + 68 + 180 = 268 кОм.

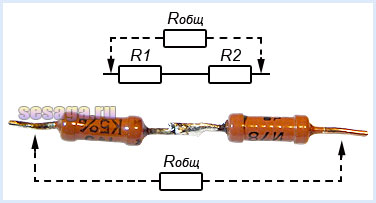
Запомните. Из нескольких соединенных последовательно резисторов их общее сопротивление Rобщ определяет тот, у которого сопротивление больше по отношению к другим резисторам в этой цепи.

Параллельное соединение резисторов

При параллельном соединении резисторов соединяются их одноименные выводы: начальные выводы соединяются в одной точке, а конечные выводы в другой. Такой способ включения облегчает прохождение электрическому току, потому что он разветвляясь, одновременно протекает по всем соединенным таким образом резисторам.

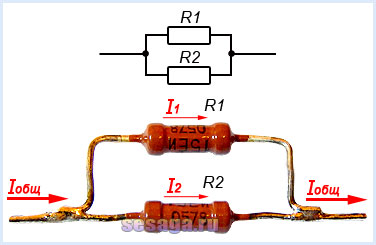
При параллельном соединении резисторов складываются не сопротивления, а их электрические проводимости (величины, обратные сопротивлениям, т.е. 1/R), поэтому общее (полное) сопротивление Rобщ уменьшается и всегда меньше сопротивлений любого резистора в этой цепи. Формула для определения полного сопротивления имеет вид:

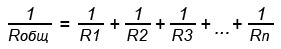
Если параллельно включены два резистора с сопротивлениями R1 и R2, тогда основную формулу немного упрощаем и получаем:

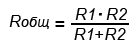
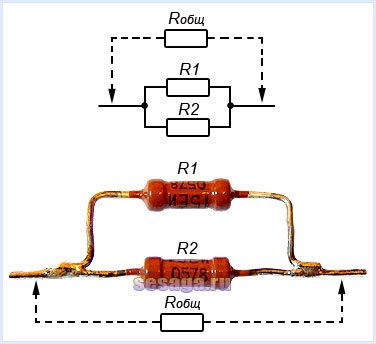
При включении трех резисторов расчет общего сопротивления будет таким:

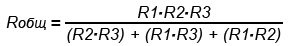
Например.
При соединении двух резисторов с номиналами R1 = 47 кОм и R2 = 68 кОм их общее сопротивление составит Rобщ = 47•68 / (47 + 68) = 27,8 кОм.

При соединении трех резисторов R1 = 10 Ом, R2 = 15 Ом и R3 = 33 Ом их общее сопротивление равно Rобщ = 10•15•33 / (15•33) + (10•33) + (10•15) = 5,07 Ом.

На заметку. При соединении двух резисторов с одинаковыми номиналами их общее сопротивление Rобщ равно половине сопротивления каждого из них.

Из приведенных примеров можно сделать вывод, что если необходим резистор с большим сопротивлением, применяют последовательное соединение. Если же резистор необходим с меньшим сопротивлением, применяют параллельное соединение.

Ну вот, в принципе, и все, что хотел сказать о последовательном и параллельном соединении резисторов. И в дополнение к статье предлагаю еще рассмотреть и смешанное соединение.
Удачи!

Последовательное и параллельное соединение резисторов

Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

• Цепь разбивают на участки с только пареллельным или только последовательным соединением.
• Вычисляют общее сопротивление для каждого отдельного участка.
• Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:

• Если резисторы соединяются последоватеьно — складывать.
• Если резисторы соединяются параллельно — использовать условное обозначение «||».
• Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»: