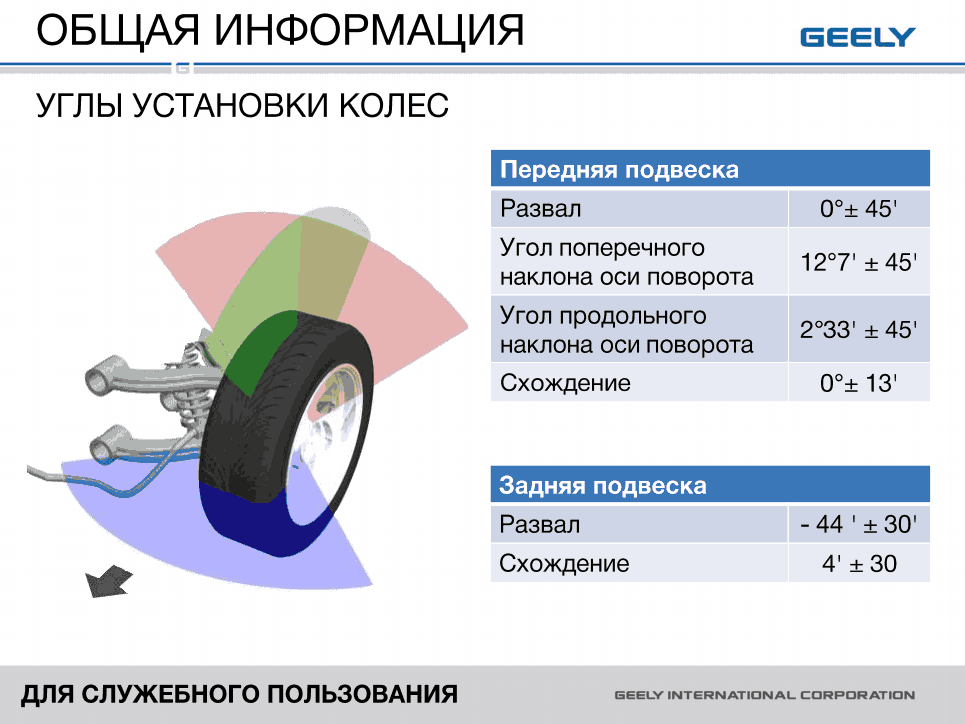
Развал-схождение.Основные углы в конструкции подвески автомобиля и ньюансы их измерения
Каждый обладатель четырехколесного друга слышал, что время от времени этому другу нужно делать так называемый «развал-схождение». Кто-то задумывался над этой проблемой довольно серьезно, иные не придавали ей особого значения: загнали утром автомобиль на ТО, вечером уплатили денежку и забрали свое транспортное средство. Тем не менее, сам автомобиль, независимо от «задумчивости» своего владельца, требует регулярного вмешательства в свою ходовую часть специалистов по «развал-схождению» – примерно один раз на пять тысяч километров пробега.Что же это за такие таинственные углы, которые так часто и тщательно нужно регулировать и выставлять? Вспомните свое далекое велосипедное детство. Родители вам приобрели или взяли напрокат трехколесный велосипед. Вы восторженно усаживаетесь в седло и начинаете лихорадочно вращать педали: раз-два! Раз-два! Мама-папа умиляются: ребенок сам едет на велосипеде!! Но вот прямая траектория заканчивается и вам нужно сменить направление движения.
Вы вращаете руль вправо (или влево) и… Ребенок упал! Ай-яй-яй! Какой неуклюжий ребенок! Ребенку срочно нужно научиться аккуратнее поворачивать! Следующие дни мама-папа учат вас поворачивать, но вы все равно падаете и падаете, испытывая комплекс неполноценности. Вот ведь большие дяди ездят на двухколесных велосипедах, поворачивают и не падают при этом. А вы! Эх, вы!Мы хотим вас обрадовать: в ваших падениях с трехколесного велосипеда вы не виноваты. Любой человек бы упал, даже большой дядя, умело катающийся на двухколесном велосипеде. Потому что вилка рулевого колеса в трехколесном велосипеде установлена перпендикулярно поверхности проезжей части. И при повороте неизбежно возникает опрокидывающая сила. Вот и вся арифметика, или, точнее сказать, физика. А в двухколесных «взрослых» велосипедах вилка руля установлена под наклоном, поэтому при повороте опрокидывающей силы не возникает. Вот этот угол и называется «углом продольного наклона оси поворота». Применяется он не только в велосипедах, но и в любой другой транспортной колесной технике.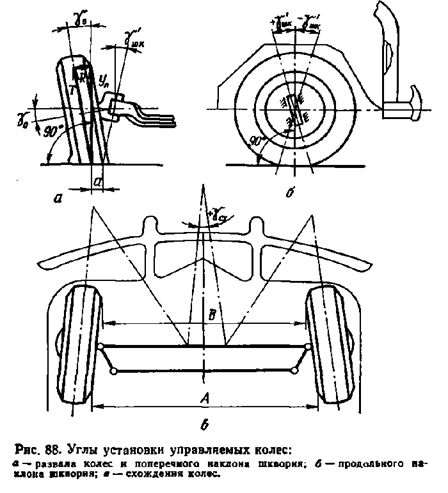
Итак, запоминаем: «угол продольного наклона (кастер) – угол между осью поворота колеса и вертикалью на виде сбоку (рис. 1)». Считается положительным, если ось наклонена назад относительно направления движения».
Рис. 1
Значение угла кастера для разных автомобилей составляет 5-7 градусов, плюс-минус один градус. Это в конструкции ходовой автомобиля самый главный угол, от которого «пляшут» все остальные. От кастера зависит устойчивость автомобиля при прямолинейном движении и способность «выходить из поворота». Начиная регулировку углов, необходимо начинать именно с кастера. Измерения «кастера» обычно требуют поворота передних колес влево-вправо, на угол от 20 до 40 градусов. Сразу доводим до вашего сведения, что иногда, в целях экономии времени, нерадивые мастера могут регулировать только развал и схождение, не трогая при этом кастер. Это неправильно. Без регулировки кастера все дальнейшие операции бессмысленны и являются просто акцией по выдаиванию из вас денежных знаков.
Итак, после регулировки кастера следующим пунктом вам должны отрегулировать угол «развала». Что такое «развал» – понять очень просто. Угол «развала» – это угол наклона плоскости колеса к перпендикуляру, установленному к плоскости дороги. Если верхняя часть колеса наклонена наружу автомобиля, то угол развала положительный, а если внутрь – то угол развала отрицательный. Угол развала в автомобиле необходим для облегчения управляемости передними колесами при условии наличия угла продольного наклона оси поворота (кастера). Если бы кастер был равен нулю, т.е. как в детском трехколесном велике, то и в развале не было бы необходимости. Угол развала у большинства автомобилей лежит в пределах от нуля до одного градуса, плюс-минус двадцать-тридцать минут.
Но не все так просто. Во-первых, угол развала (из-за наличия кастера) зависит от угла поворота переднего колеса. То есть, угол развала – величина непостоянная. Поэтому при регулировке мастера пользуются таблицами, в которых угол развала на тот или иной автомобиль указан для положения передних колес при движении «прямо».
Отсюда возникает необходимость определять такое положение передних колес при измерении и регулировке развала, и зачастую это делается так называемым методом «привязки к задней оси».
Во-вторых, угол развала зависит от пригруженности автомобиля. Для большинства автомобилей в таблицах приводятся данные для пригруженного автомобиля. При этом существует несколько схем загрузки. Наиболее универсальная схема загрузки – это установка на каждом пассажирском месте (а также в багажнике) по 70 кг груза (например, мешочки с песком или со свинцовой дробью), при этом бензобак должен быть заправлен полностью.
Здесь также вас могут подстерегать опасности получения некачественной услуги. Если вам при регулировке развала не нагружали автомобиль – у вас скорее всего будет неправильно выставлен угол развала. У автора этих строк неоднократно бывали случаи, когда на вопрос «почему не пригружаете автомобиль?» ответом был отказ от дальнейшего обслуживания: горе-мастера «слишком умного клиента» боятся как огня.
Хотя есть некоторые марки автомобилей, для которых углы развала в справочниках приводятся для ненагруженного автомобиля.
Само собой разумеется, что при измерении и регулировке углов элементы ходовой автомобиля (сайлент-блоки, наконечники, шаровые опоры и т.п.) должны быть в целости и сохранности, ходовая не должна иметь люфтов, зазоры должны быть в норме, равно как и давление во всех шинах. Колеса должны иметь одинаковый износ, не допускается вариантов, например, когда три колеса нормальные и новые, а одно – «лысая» запаска.
И, наконец, последний регулируемый угол – это угол схождения колес. Схождение может измеряться как в линейных единицах (миллиметрах), так и в угловых (минутах и секундах). Схождение регулируется в последнюю очередь. Согласно определению, схождение – это угол между продольной осью автомобиля и плоскостью вращения колеса, проходящей через центр шины управляемого колеса (рис. 3). Схождение считается положительным, если плоскости колес пересекаются перед автомобилем, и отрицательным, если они пересекаются сзади.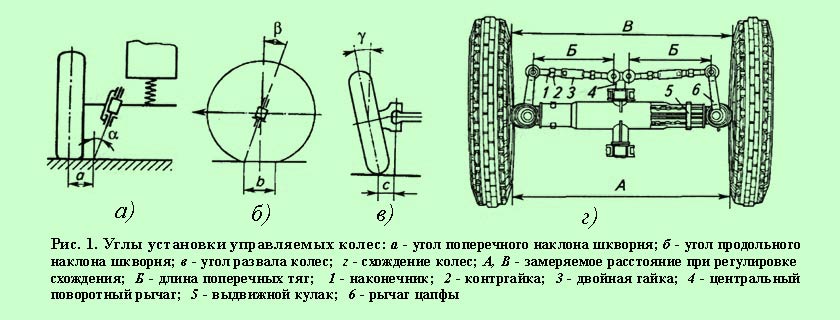
Если схождение измеряется в угловых единицах, то величина схождения не зависит от диаметра колеса. Напротив, если схождение измеряют в миллиметрах, то нужно учитывать размеры дисков. При одном и том же угловом значении схождения у колеса с диаметром 17 дюймов линейное схождение будет больше, чем у колеса с диаметром 13 дюймов. Компьютерные стенды делают коррекцию автоматически, но оптические и лазерные устройства требуют пересчета миллиметров с учетом диаметра колеса. Если же измерение осуществляется в угловых единицах, то, повторимся, пересчетов не требуется.
В США схождение измеряется в частях дюйма и обычно устанавливается близко к нулю, что означает, что колеса параллельны друг другу. Термин «схождение» подразумевает, что передние части шин ближе друг к другу, чем задние. Термин «расхождение» (или «отрицательное схождение») означает обратное: задние части шин ближе друг к другу, чем передние. Неправильное схождение влечет за собой быстрый одинаковый износ шин.
Кроме регулируемых углов, ходовая часть имеет еще один нерегулируемый угол – угол поперечного наклона оси поворота колеса (KPI).
Предназначение этого угла – также стабилизация прямолинейного движения и «выход из поворота» под действием силы тяжести автомобиля. Этот угол некоторые лазерные стенды просто «не видят». Однако бывают случаи, когда после регулировки углов кастера, развала, схождения автомобиль все равно плохо держит дорогу. Тогда нужно смотреть угол поперечного наклона, возможно все дело в нем. Повторимся, этот угол не регулируется, но он конструктивно выполняется на заводе-изготовителе. Если при измерениях видно, что угол поперечного наклона существенно отличается от заводского значения, значит, произошел сильный износ конструкции ходовой части, или вообще автомобиль был сильно поврежден при ДТП.
Таким образом, для «развальщиков» вырисовывается еще один прибыльный бизнес: измеряя все углы, а не только «развал-схождение», становится возможным давать экспертную оценку состоянию автомобиля: побывал он в ДТП или нет. Ведь если у автомобиля серьезно (и несимметрично) нарушены углы продольного и поперечного углов наклона оси поворота (кастер и КПИ соответственно), то вполне вероятно, что автомобиль «ударен».
А если еще и проконтролировать такие параметры, как «смещение мостов» и «перекос оси», то экспертную оценку можно сделать почти со 100%-й точностью. А это особенно важно для «глубинки», куда могут сплавлять битые автомобили нечистые на руку «бизнесмены».
И, в заключение, о еще одном виде углов, подлежащим измерению на автомобиле, особенно в свете прохождения транспортными средствами государственного техосмотра. Это максимальный угол поворота колеса, а также соотношение углов поворота передних колес. При повороте автомобиля внутреннее колесо должно поворачиваться по дуге меньшего диаметра, чем внешнее. С этой целью в конструкцию транспортного средства вводятся такие элементы, как рулевая трапеция, дифференциалы и т.п. Однако нам нужно просто, не вдаваясь в подробности, понять, что и как измерять. Для измерений углов поворота передних колес служат поворотно-сдвижные круги с угловыми шкалами. При повороте, например, влево, левое (внутреннее) колесо поворачивается на величину 20°, при этом правое (внешнее) колесо должно поворачиваться (в зависимости от вида автомобиля) на величину 18-18,5°.
Несоблюдение этого правила влечет за собой пробуксовку колес и плохой «вход в поворот».
Итак, мы рассмотрели основные углы в конструкции подвески автомобиля и ньюансы их измерения. Часто спрашивают: какой стенд лучше использовать на СТО – лазерный или компьютерный? Если бы эти стенды стоили одинаково, то мы бы рекомендовали отдавать предпочтение компьютерным – вследствие их большей производительности. Но коль скоро зачастую стоимость отличается более, чем на порядок, то вам нужно определиться, для чего вам нужен стенд развал-схождения: для имиджа или для работы? Всегда нужно помнить золотое правило: клиент «идет» не на стенд, а на хорошего мастера. Иногда быстродействие компьютерного стенда нивелируется и сводится на нет неумелым его использованием. Поэтому все зависит от ваших финансовых возможностей, поставленных целей и вашего умения. Удачи вам в жизни и бизнесе!
Константин Павляк
Угол схождения колес — Энциклопедия по машиностроению XXL
Угол схождения 6 управляемых колес (рис.
151, б) определяется разностью расстояний А V. Б между колесами, которые замеряют сзади и спереди по краям ободьев на высоте оси колес. Угол схождения колес у разных автомобилей находится в пределах 0°20 — 1°, а разность расстояний между колесами сзади и спереди 2—12 мм. В процессе эксплуатации углы схождения колес могут изменяться из-за износа втулок шкворней поворотных кулаков, шарнирных соединений рулевой трапеции и деформации ее рычагов. Регулировку угла схождения в эксплуатации производят изменением длины поперечной рулевой тяги..
[c.226]
Угол схождения управляемых колес (рис. 71, б) определяют разницей расстояний между их горизонтальными диаметрами в передней и задней частях колес. Эта разница должна быть в пределах от 2 до 12 мм (размер Б меньше размера Л). Схождение колес обеспечивает их параллельное качение при наличии развала, зазоров в шкворнях, тягах и подшипниках. Угол схождения колес устанавливают изменением длины поперечной рулевой тяги.
Балка 10 передней оси, рычаги 7, соединенные с поворотными цапфами, и поперечная тяга 12 образуют рулевую трапецию. На резьбовых концах поперечной тяги установлены закрепленные стяжными болтами наконечники с резьбой. Правый наконечник имеет правую резьбу, а левый — левую. Вращением поперечной тяги можно изменять расстояние между рычагами 7, регулируя угол схождения колес. [c.164]
Установить шаровые пальцы поперечной рулевой тяги, с тягой в сборе, надеть защитную накладку с обоймой и отражатель и отрегулировать угол схождения колес [c.508]
Отрегулировать угол схождения колес ввертыванием трубы поперечной рулевой тяги в головки и установить угол поворота колес упорными болтами [c.520]
Угол схождения колес определяется разностью (Л Б) размеров [c.286]
Угол схождения колес (разность расстояний А я Б между внутренними краями шин, замере[шых в одной горизонтальной плоскости), равный 1,5—3 льм.
[c.148]
Угол схождения колес необходим для компенсации угла развала колес, стремящегося заставить колесо двигаться по расходящимся дугам, и обеспечения качения колеса по дороге без скольжения. [c.151]
Иными словами, угол схождения колес определяется величиной угла их развала чем больше угол развала, тем больше должно быть схождение. [c.151]
В процессе эксплуатации автомобиля необходимо периодически проверять угол схождения колес и при обнаружении отклонений отрегулировать его.
Особенности сборки передних мостов. Основными операциями при сборке переднего моста грузовых автомобилей являются установка поворотных цапф с рычагами, поперечной и продольной тяг и ступиц с тормозными барабанами. Большое значение для нормальной работы собранного автомобиля имеет проверка правильности монтажа поворотных цапф и колес и регулировка подшипников ступиц передних колес. При этом необходимо соблюдать правильность установки углов колес и наклона шкворней а — угол развала колес, образуемый вертикальной плоскостью с плоскостью вращения колес ф — угол схождения колес, определяемый практически разностью расстояний Л и р — угол наклона шкворня вбок, образуемый осью шкворня с вертикальной плоскостью, проходящей через продольную ось автомобиля у — угол наклона шкворня назад, образуемый осью шкворня с вертикальной плоскостью, перпендикулярной к оси автомобиля.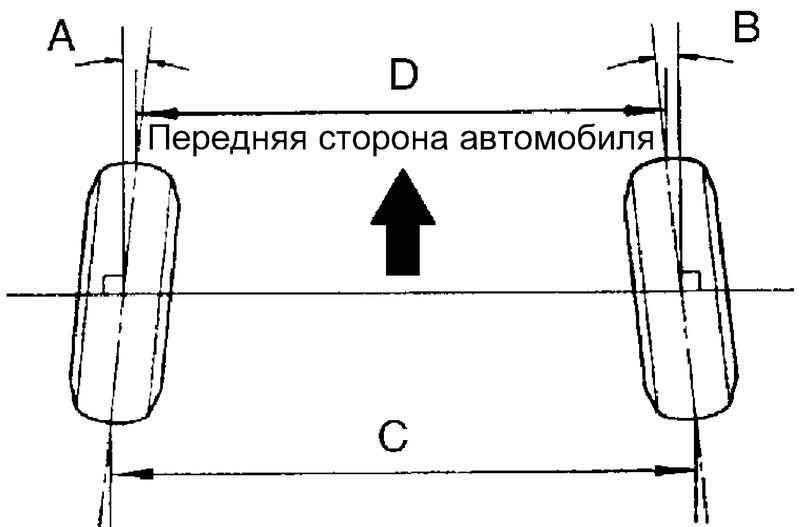
В грузовых автомобилях регулируется лишь угол схождения колес. Что касается остальных углов, то они обеспечиваются самой конструкцией передней оси и поворотных цапф и при отсутствии прогиба оси, износа шкворней кулака, поломки или осадки рессор углы практически почти не изменяются. [c.452]
Углы развала колес и наклона шкворня регулируются при помощи эксцентрикового резьбового пальца. Угол схождения колес проверяется аналогично описанному для других автомобилей. Собранные передние мосты желательно проверять и регулировать на специальных стендах. Для примера на фиг. 360 приведен стенд для регулировки передних мостов автомобиля ЗИС-150.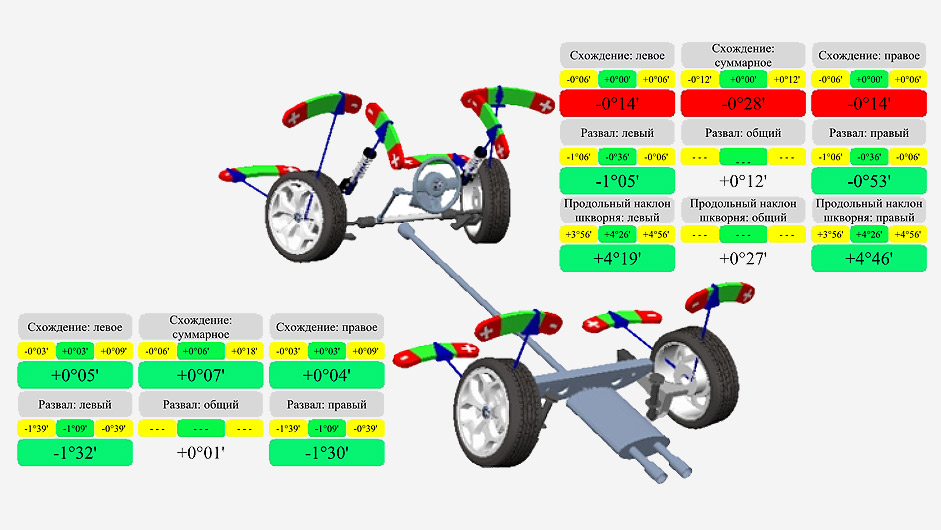
Поперечная штанга посредством шаровых шарниров соединена с боковыми штангами, которые с свою очередь соединены с рычагами поворотных цапф при помощи шаровых шарниров с автоматическим устранением зазора между сухарями и пальцем. Такие наконечники не требуют регулировки. Наконечники завернуты в штанги, что позволяет регулировать угол схождения колес. [c.590]
Различают следующие углы установки колес угол развала у, углы наклона шкворней — поперечный р и продольный а и угол схождения колес б (рис. 24). [c.50]
Требуют регулярной проверки углы установки передних колес, так как вследствие износа и деформации деталей углы во время эксплуатации могут изменяться. При правильном угле развала разность расстояний Я и В должна быть 7—11 мм (рис.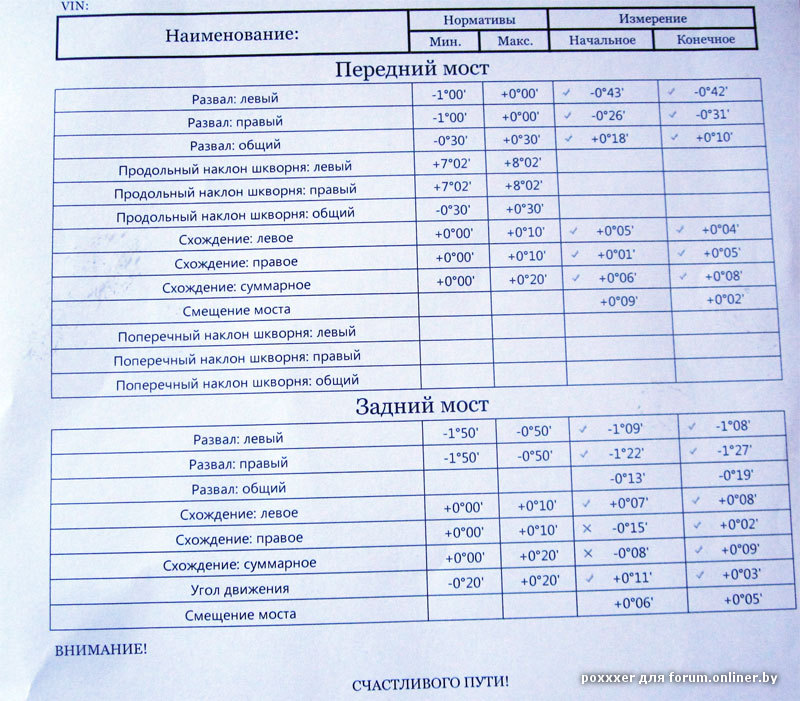
Угол схождения колес выражается в разности расстояний между кромками ободов колес на уровне их центра спереди и сзади. Расстояние впереди всегда меньше, чем сзади (положительный угол). Угол схождения служит для устранения разворачивающего момента на колесе и ликвидации бокового проскальзывания, так как сила сопротивления качению стремится повернуть колесо наружу. Отклонение от регламентированного угла схождения проявляется в возрастании усилия поворота рулевого колеса с последующим появлением пилообразного износа рисунка протектора покрышки.
Согласно стандарту ДИН 70020 схождение V есть разность размеров ВС (рис. 4.6.1), равных расстоянию между внутренними закраинами ободьев передних колес соответственно в задней и передней частях ободьев. Схождение измеряется на уровне высоты центров колес при прямом положении колес и согласно стандарту ДИН 70020 (часть 1, выпуск — сентябрь 1976 г.
) в снаряженном состоянии (см. табл. 4.1.1). Угол схождения колеса, выраженный
[c.303]
Колеса автомобиля при движении должны катиться параллельно друг другу в направлении движения по прямой. Наличие хотя бы незначительных люфтов в сочленениях рулевых тяг, в подшипниках колес и во втулках шкворней приводит к повороту каждого колеса на некоторый угол (правого — направо и левого — налево). Это вызывает проскальзывание покрышек и резкое увеличение их износа. Чтобы не допустить проскальзывания колес при движении, их устанавливают с некоторым схождением, т. е. расстояние Б между ободами колеса спереди должно быть меньше, чем расстояние А сзади оси (рис. 155, в). Величина схождения колес А—Б) показана в табл. 6.
[c.236]Ход колес в вертикальной плоскости не превышает 200 мм. Угол развала задних колес составляет 2°, поперечный наклон шкворня Т. Наклон шкворня вперед и схождение колес отсутствуют. Максимальные углы поворота колес наружного 46°30 внутреннего 70°.
[c.72]
Установка управляемых колес с одновременным развалом и схождением обеспечивает их прямолинейное качение по дороге без бокового скольжения. При этом должно быть правильно подобрано соотношение между углами развала и схождения. Каждому углу развала соответствует определенный угол схождения, при котором сопротивление движению, расход топлива и износ шин будут минимальными. Обычно оптимальный угол схождения управляемых колес составляет в среднем 15—20% от угла их развала. Однако в процессе эксплуатации управляемые колеса часто устанавливают со схождением несколько большим, чем требуется для компенсации их развала. Это вызвано тем, что у колес вследствие наличия зазоров и упругости рулевого привода может появиться отрицательное схождение. В результате даже при положительном их развале возрастают сопротивление движению и износ шин.
Схождение колес, мм 1,5…3 2…5 2…5 3…8 О…2 Угол V наклона шкворня 3°30 3°30 3°10 2°1Г 5° назад [c.
126]Передние колеса, имеющие развал, будут катиться без скольжения покрышки по дороге в том случае, если при движении они будут иметь некоторый угол схождения. Развал колес обусловливает стремление их катиться по расходящимся дугам. Во избежание неравномерного износа покрышек необходимо, чтобы колеса имели такой угол схождения, который заставлял бы их катиться по сходящимся ЛИНИЯЛ1. Таким образом, угол схождения колес определяется величиной их развала чем больше развал, тем больше схождение.
[c.286]Угол схождения колес в этом случае определяется разностью размеров А—Б между внутренними краями шин (см. рис. 87) или между фланцами ободов в горизонтальной плоскости на уровне оси передних колес. Измерение следует производить специальной линейкой. По окончании регулировки необходимо установить наконечники поперечной тяги так, чтобы их головки находились в одной плоскости, затянуть и зашплинтовать гайки болтов кле.ммовых соединений наконечников поперечной рулевой тяги.
[c.151]
Одной из основных операций сборки передних мостов или передних подвесок должна быть проверка правильности установки перед, них колес. Для легкости управления и повышения устойчивости движем ния автомобиля кЬнструкцией передних мостов (подвесок) предусмотрены углы развала передних колес, схождения передних колес, наклона шкворней поворотных кулаков назад, наклона шкворней вбок, На фиг. 356 показаны схемы установки углов колес и наклонг шкворня. На фиг. 356 а — угол развала колес, образуемый вертикальной плоскостью с плоскостью вращения колеса 8 — угол схождения колес, определяемый практически разностью расстояний А б — угол наклона шкворня вбок, образуемый осью шкворня с вертикальной плоскостью, проходящей через продольную ось авто
В грузовых автомобилях, а также в автомобиле Москвич , регу-фуется лишь угол схождения колес. Что касается остальных углов, таковые обеспечиваются самой конструкцией передней оси и пово-
[c.
593]
Угол схождения колес регулируется с помощью поперечной ру-юй тяги и проверяется по разности расстояний между внутренними 1ями ободов колес, замеряемых спереди и сзади на уровне оси ко-Кроме угла схождения колес, необходимо отрегулировать угол юрота передних колес. На фиг. 357 показан эскиз регулировки 1а поворота передних колес автомобиля ЗИС-150. Угол поворота 1ес здесь устанавливается с помощью упорных болтов на левом по-. ютном кулаке. [c.593]
Угол схождения колес д пределя-ется разностью расстояния между колесами одной оси, замеренными сзади и спереди по краям ободьев на вьюоте оси колес (рис. 5.46 — б). [c.108]
Износ шин, как правило, возникает кок следствие неправильной установки углов схождения. При больших значениях положительного угла схождения (плоскости колес сходятся) пилообразный износ возникает на наружных дорожках протектора. При больших значениях отрицательного угла схождения (плоскости колес расходятся) износ возникает на внутренних дорожках.
Отрегулировать угол схождения колес. Проверко эффективности регулировки — испытание на выбег автомобиля (расаояние, которое автомобиль проходит накатом со скоростью, например 50 км/ч, до оаоновки). Выбег измерять как до регулировки угла, ток и после регулировки. Если величина выбега увели-
[c.87]
Установка передних колёс характеризуется следующими углами угол наклона вертикальной оси колеса, угол схождения передних колёс в плане, угол наклона по воротною шкворня вбок и угол наклона нижнею конца поворотного mKBO.jHH вперёд. [c.102]
Большое влияние на износ протектора оказывают углы установки колес. Наиболее важным яг шется угол схождения. He ooтвeт т e его оптимальной величине резко сказывается на ресурсе шин (рис. 11.7). [c.211]
Угол схождения | Shod-Razval.Info
Угол схождения колёс Wheel Toe (отклонение колеса) отклонение колеса от прямой.
Для чего нужно схождение? Схождение колёс компенсирует кинематическое воздействие трансмиссии, тормозов и конструктивные особенности подвески и обеспечивает правильное направление колес и устойчивое движение автомобиля.
В других источниках приводится другое определение, которое предназначено для грузовых автомобилей с зависимой подвеской и с задним приводом. К сожалению, встречается информация, как правило, материал взят из старых учебников или написано дилетантами #1 или скопирована с другого источника #2.
Угол схождения Toe angle – это угол в горизонтальной плоскости, между направлением движения автомобиля в продольной плоскости и плоскостью вращения колеса (см. рис. 103).
рис. 103 Угол схождения
Положительное схождение Toe—in (P = positive «+»)
При положительном схождении, передняя часть колеса повёрнута во внутрь, колёса сходятся или плоскости вращения колеса пересекаются впереди (см.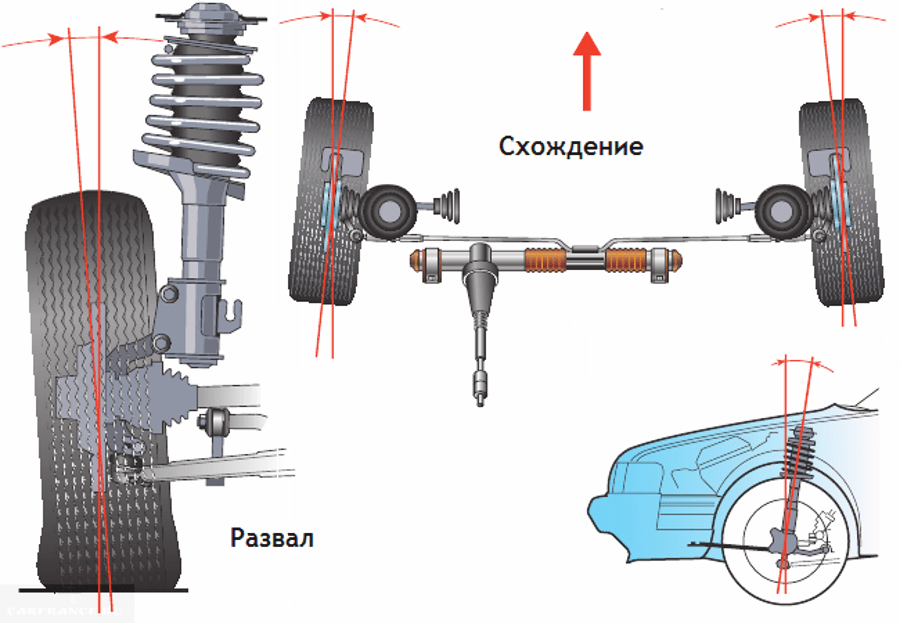
рис. 104).
рис. 104 Положительное схождение
Отрицательное схождение Toe—out (N = negative, «-»)
При отрицательном схождении, передняя часть колеса повёрнута в наружу, колёса расходятся или плоскости вращения колеса пересекаются сзади (см. рис. 105).
рис. 105 Отрицательное схождение
Величина угла схождения.
Величину угла схождения, можно измерять в угловых величинах градусах (degree) (см. рис. 106) и в линейных величинах в миллиметрах (мм), или дюймах (Inches) (см. фото. 107).
Величина угла схождения Size toe angle.
Общее схождение Total toe in. Подразумевается сумма двух углов схождения колёс и выражается по формуле в угловых величинах,
t = tl + tr
или разница расстояний между дисками колёси впереди и сзади и выражается по формуле в линейных величинах,
t = At – Bt где At = Al + Ar и Bt = Bl + Br (см.
рис. 108).
рис. 108 Схождение Toe
Индивидуальный угол схождение Individual Toe Angle Угол схождение одного колёса. Подразумевается величина угла схождения каждого колеса в отдельности и выражается,
tr или tl
или разница расстояний между дисками колёси и осевой линией автомобиля, впереди и сзади и выражается по формуле,
tl = Al – Bl или tr = Ar – Br (см. рис. 108).
Неправильный угол схождения.
В процессе эксплуатации автомобиля происходит износ и деформация узлов и деталей рулевого управления, подвески и кузова автомобиля, это приводит к изменению углов установки колёс.
Для компенсации износа и деформация узлов и деталей рулевого управления, подвески и кузова автомобиля, может потребоваться замена и дополнительная регулировка углов колёс.
Неправильная установка углов схождения, может повлиять на устойчивость, стабильность и управляемость автомобиля.
Повышенное положительное или отрицательное схождение приводит к износу шин, увеличению расхода топлива и рыскание автомобиля (неустойчивость, нестабильность автомобиля в колее).
Если положительный угол схождения слишком велик, то будет изнашиваться наружная половина шины (см. фото. 109).
фото. 109 Повышенный положительный угол схождения, износ шин.
Если отрицательный угол схождения слишком велик, то будет изнашиваться внутренняя половина шины (см. фото. 110).
фото. 110 Повышенный отрицательный угол схождения, износ шин.
Если велика разница углов схождения с левой стороны и с правой стороны, руль будет стоять не ровно, в сторону более положительного угла для передней оси (см.
рис. 112).
рис. 112 Разница углов схождения передней оси, руль не ровно.
Если велика разница углов схождения с левой стороны и с правой стороны, руль будет стоять не ровно, в сторону более отрицательного угла для задней оси (см. рис. 119).
рис. 119 Разница углов схождения задней оси, руль не ровно.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.ТЕГИ}} {{$элемент}} {{l10n_strings.
ПРОДУКТЫ}}
{{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.ЯЗЫК}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}} {{l10n_strings.
AUTHOR_TOOLTIP_TEXT}}
Дистанционное зондирование | Бесплатный полнотекстовый | Точность геопозиционирования с использованием изображений с нескольких спутников: стереоизображения IKONOS, QuickBird и KOMPSAT-2
1.Введение
Спутниковые изображения высокого разрешения широко используются в качестве основного источника для геопозиционирования, поскольку они обеспечивают множество преимуществ, таких как широкий охват, короткое время просмотра и соответствующее пространственное разрешение, необходимое для крупномасштабного картографирования.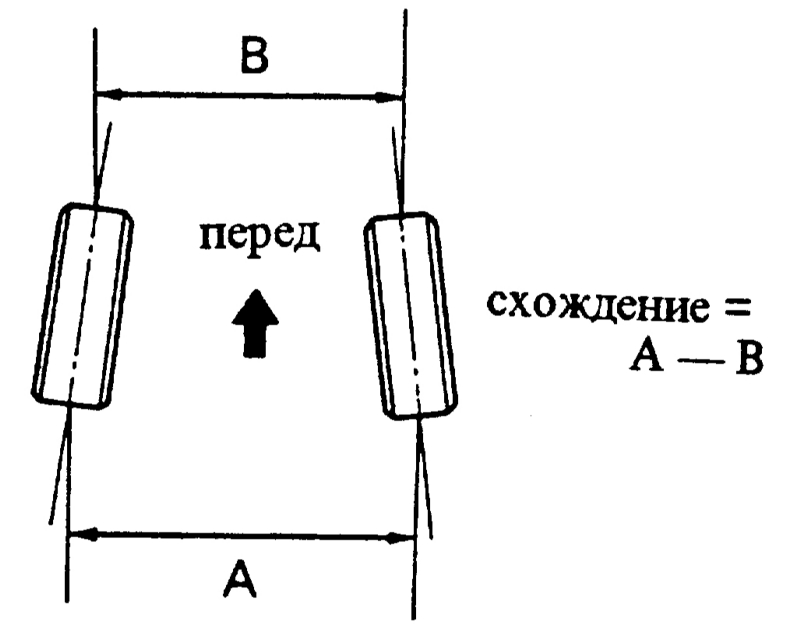
Во многих исследованиях изучался потенциал спутниковых изображений высокого разрешения для геопозиционирования. Точность их позиционирования предпочтительно проверялась с использованием наземных точек, полученных из изображений IKONOS [1,2]. Ногучи и др. [3] и Тонг и др.[4] исследовали точность отображения с помощью геометрической коррекции изображений QuickBird [3,4]. Исследования показали, что на изображениях IKONOS и QuickBird с точной географической привязкой может быть достигнута точность около 1–2 м или выше. Аналогичные исследования проводились для различных изображений, таких как SPOT-5 и FORMOSAT-2 [5,6]. Недавно точность географической привязки изображений Geoeye-1 и WorldView-1/2 была описана как около метра как в горизонтальной, так и в вертикальной плоскостях [7,8,9,10]. Перечисленные выше исследования достаточно продемонстрировали потенциал спутниковых изображений высокого разрешения для точного геопозиционирования.Однако они основаны на соглашении об использовании пар изображений с одного спутника, полученных в пределах одного и того же спутника.
Доступность пар от одного и того же датчика нельзя предполагать постоянно, и, в частности, сильное использование таких пар может наложить некоторые ограничения на широкое применение спутниковых изображений. Чтобы преодолеть такие ограничения, необходимо разработать методы интеграции изображений, полученных с нескольких спутников. Замена или улучшение обычных односпутниковых стереоизображений многоспутниковыми изображениями будет очень полезно для реальных картографических приложений.Например, интеграция с двумя спутниками может решить проблему отсутствия стереоизображений с одного спутника или интеграции дополнительных изображений для повышения точности существующих стереоизображений. В связи с этим важно исследовать точность позиционирования, достижимую с помощью изображений с нескольких спутников.
В другом исследовании анализировалась точность топографического картографирования, достигнутая путем объединения двух изображений с разным разрешением с использованием отдельных изображений из IKONOS, QuickBird и SPOT-5 [12]. Однако эти исследования были больше сосредоточены на применимости трехмерной аффинной модели для моделирования спутниковых датчиков, чем на интеграции изображений. Недавно Jeong and Kim (2014) исследовали геометрию изображения и точность позиционирования стереоданных с двумя датчиками путем интеграции двух разных спутников [13]. В основном они сравнивали различия в геометрических характеристиках стереопар с одним и двумя датчиками и подчеркивали, что такие различия следует рассматривать как важные при обработке стереоизображений с двумя датчиками.Предыдущие исследования выявили точность геопозиционирования и геометрические характеристики по изображениям с нескольких спутников. В частности, Ли и соавт. [11] обеспечили точность геопозиционирования, используя результаты интеграции трех или более изображений, тогда как в других исследованиях проверялась интеграция только двух изображений.
Однако их главной задачей было подтвердить потенциал интеграции IKONOS-QuickBird для геопозиционирования и проверить ее точность. Вопросы обоснованности, практические случаи и важные соображения не были тщательно исследованы.В этом документе утверждается, что характеристики точности по сравнению с традиционно используемыми парами, полезные примеры и некоторые руководящие принципы должны быть исследованы или пересмотрены, прежде чем использование нескольких спутниковых изображений может быть рекомендовано пользователям дистанционного зондирования в качестве основного источника для картографических приложений. Таким образом, в этой статье исследуется точность позиционирования изображений с нескольких спутников и оценивается их пригодность для геопозиционирования путем сравнения их точности с точностью типичных стереоизображений с одного спутника.Во-первых, двухспутниковая интеграция сравнивается с односпутниковой стереоизображением. Этот эксперимент проверяет, есть ли какая-либо разница между достижимой точностью и может ли первая заменить вторую для реальных картографических приложений.
Во-вторых, исследуется изменение точности при включении дополнительных изображений в односпутниковое стерео. Этот эксперимент проверяет, всегда ли интеграция изображений с более высоким разрешением является эффективным средством повышения точности существующих стереоизображений.Наш анализ показывает потенциал и ограничения этого подхода, а также важные соображения по обработке изображений с нескольких спутников в картографических приложениях.
2. Экспериментальные данные и датчик модели
Были собраны и использованы для наших экспериментов три пары стерео изображений IKONOS, стерео QuickBird и стерео KOMPSAT-2 Тэджона, Корея.
Свойства изображений показаны в таблице 1, где сцены пронумерованы в порядке получения. Для каждой стереопары были представлены угол конвергенции и угол подъема биссектрисы (BIE), чтобы показать стабильность геометрии изображения. Эти два угла показаны на рисунке 1. Угол схождения — это угол между двумя лучами стереопары, тогда как угол BIE — это угол возвышения биссектрисы угла схождения. Угол BIE обычно указывает на наклонность эпиполярной плоскости. Угол конвергенции и его влияние на стереокартографирование постоянно рассматривались, но влияние угла BIE было введено только недавно [13].Предыдущие исследования показали, что небольшой BIE может снизить точность отображения стереоданных. Настоящее исследование считает, что такие эффекты угла BIE также могут быть важны для интеграции трех или более источников данных, а также стереоданных. Эти два угла включены в метаданные или могут быть рассчитаны через углы азимута и места [11,13]. Большинство спутников создают стереопары с помощью своих конкретных принципов получения изображений.
Например, стереозвук QuickBird получается путем наклона вперед и назад по оси тангажа при сохранении угла крена, близкого к 0°, тогда как стереозвук KOMPSAT-2 получается путем наклона угла вдоль оси крена при сохранении угла тангажа, близкого к 0°.Эти подходы обеспечивают достаточный угол конвергенции и угол BIE почти 90°, как показано в Таблице 1. В случае стереосистемы IKONOS углы конвергенции и BIE также ограничены нормальными диапазонами за счет использования двух изображений, снятых с регулярными интервалами азимутального угла, хотя они измеряется путем одновременного наклона датчика по осям крена и тангажа.Рисунок 1. Представление углов схождения и BIE в стереогеометрии.
Рисунок 1. Представление углов схождения и BIE в стереогеометрии.
Таблица 1. Свойства экспериментальных данных.
94.1 °0 47.68 °0 75.53 °0 89.34 °| QuickBird | KOMPSAT-2 | KOMPSAT-2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Сцена-1 | Сцена-2 | Сцена-1 | Сцена-2 | Сцена-1 | Сцена-2 | |||
| Дата приобретения | 7 февраля 2002 г. | 7 февраля 2002 | 16 января 2005 | 16 января 2005 г. | 16 января 2005 г. | 10 мая 2007 | 6 мая 2008 г. | |
| Азимутальный угол | 338.1 ° | 234,9 ° | 199.9 ° | 199.5 ° | 5.2 ° | 79.7 ° | 79.7 ° | 256.7 ° |
| Угол возвышенности | 66.5 ° 170071 | 68,4 ° | 59,5 ° | 58,7 ° | 58. 2 ° | 74.1 ° | ||
| Угол конвергенции | 35.00 ° | 61.27 ° | 61.27 ° | |||||
| BIE Угол | 85.74 ° | |||||||
| GSD (столбец / ряд) | 0.90 м / 0,96 м | 0,92 м / 0,90 м | 0,71 м / 0,79 м | 0,71 м / 0,83 м | 1,30 м / 1,10 м | 1,04 м / 1,01 м | ||
Всего для экспериментов было использовано 30 опорных точек, состоящих из двух типов: 12 модельных опорных точек и 18 независимых контрольных точек (НКТ). Опорные точки модели используются для обновления начальных коэффициентов модели, представленных в метаданных, и для установления моделей датчиков, тогда как ICP используются отдельно для оценки точности геопозиционирования стереопар.Все GCP были получены с помощью измерений глобальной системы позиционирования (GPS) в полевых условиях и обработаны дифференциальной обработкой GPS для обеспечения точности лучше 10 см. В этой статье модель датчика рациональной функциональной модели (RFM), предложенная Grodecki и Dial [ 2] использовался для моделирования и объединения нескольких спутниковых изображений. Поскольку используемые модели датчиков были полностью описаны в предыдущей работе, здесь дано лишь краткое описание. Уравнения модели выражаются следующим образом:rn = P1(Xn, Yn, Zn)P2(Xn, Yn, Zn)
(1)
cn = P3(Xn, Yn, Zn)P4(Xn, Yn, Zn)
(2)
P1 (Xn, Yn, Zn) = A1 + A2xn + A3YN + A4ZN + A5xnyn + A6xnzn + A7nzn + A8xn2 + A9yn2 + A10Zn2 + A11xnynzn + A12xn3 + A13xnyn2 + A14xnzn2 + A15xn2n2 + A16yn3 + A17ynzn2 + A18xn2Zn + A19yn2Zn + A20ZN2
(3)
где (rn, cn) — нормированные строка и столбец в пространстве изображения; (Xn, Yn, Zn) – нормированные долгота, широта и эллипсоидальная высота соответствующих им наземных координат в пространстве объекта.
Параметры a1, a2, … и a20 — это коэффициенты полиномиальной функции P1, а коэффициенты P2, P3 и P4 определяются аналогично. Коэффициенты модели были извлечены из файлов коэффициентов рационального полинома (RPC), предоставленных поставщиком. Двенадцать опорных точек модели использовались для компенсации ошибок в коэффициентах модели, а затем уравнения модели были точно обновлены. Для компенсации ошибок в пространстве изображений использовались следующие уравнения [2]:∆p = a0 + ac∙Столбец+ ar∙Строка
(4)
∆r = b0 + bc∙Столбец+ br∙Строка
(5)
где ∆p и ∆r — регулируемые функции в направлениях столбца и строки соответственно, а a0, ac, ar, b0, bc, br — параметры настройки изображения, которые можно оценить методом наименьших квадратов.Рисунок 2. Покрытие изображений и распределение опорных точек.
Рисунок 2. Покрытие изображений и распределение опорных точек.
3. Тестовые примеры использования изображений с нескольких спутников
Два сценария интеграции были исследованы для проверки применимости изображений с нескольких спутников для геопозиционирования.
Первый случай включает двухспутниковую интеграцию с использованием двух разных спутниковых изображений. Достигнутые точности картографирования сравнивались с таковыми при односпутниковом стерео.Будет интересно сравнить двухспутниковое стереоизображение, интегрированное с двумя разными разрешениями, с односпутниковым стереоизображением, снятым с более высоким или более низким разрешением. Такое сравнение исследует, можно ли использовать интеграцию с двумя спутниками для полной компенсации отсутствия стереоизображения с одного спутника.
Второй случай объединяет три или более изображений. Полученная точность картирования также сравнивалась с точностью односпутникового стерео, включая сравнение точности картирования до и после интеграции изображений с более высоким разрешением.В реальных картографических приложениях может быть очень полезно проверить случаи, в которых интеграция дополнительных изображений повышает точность односпутникового стерео, и определить, есть ли какие-либо важные соображения для такой интеграции.
Рисунок 3. Тестовые случаи для сравнения между стереосистемой с одним спутником и интеграцией с двумя спутниками. ( a ) стерео с одним спутником, ( b ) стерео с двумя спутниками.
Рисунок 3. Тестовые случаи для сравнения между стереосистемой с одним спутником и интеграцией с двумя спутниками. ( a ) стерео с одним спутником, ( b ) стерео с двумя спутниками.
Кроме того, нам необходимо рассмотреть еще один элемент, который может повлиять на двухспутниковую картографию.Поскольку точность отображения двухспутникового стерео, в отличие от односпутниковых стереопар, тщательно не исследовалась, необходимо учитывать множество переменных. В частности, результаты — когда геометрия односпутниковых и двухспутниковых стереосистем одинакова или обе стабильны — используются для проверки того, влияет ли на точность картирования какой-либо другой элемент, помимо разрешения изображения и геометрии. Для этого эксперимента мы анализируем три стереопары с одним спутником и 12 интеграций с двумя спутниками.
Для второго случая мы исследуем, например, различия в точности, когда одиночные изображения QuickBird или IKONOS с более высоким разрешением (рис. 4) или стереоизображения (рис. 5) интегрируются в стереоизображения КОМПСАТ-2. Как и прежде, при рассмотрении разрешения изображения можно ожидать, что такие интеграции повысят точность стереоизображения КОМПСАТ-2. Однако в этом случае необходимо помнить, что геометрические отношения между всеми изображениями могут влиять на точность сопоставления, и поэтому нам необходимо проверить, не приведет ли дополнительное изображение к слабой геометрии с любым из существующих изображений.Мы также исследуем, есть ли разница между интеграцией одиночного изображения и интеграцией стереоизображений. Для экспериментов мы проводим шесть типов интеграций для тестовых случаев, как показано на рисунке 4, и четыре типа интеграций для тестовых случаев, как на рисунке 5. изображений или интеграцию изображений с более низким разрешением из нескольких спутниковых изображений. Однако мы не смогли извлечь никакой полезной информации из таких интеграций.Например, интегрирование изображений более низкого разрешения всегда снижало точность существующих пар, и поэтому мы не рассматривали их результаты далее в этой статье.Рисунок 4. Тестовые случаи для сравнения до и после интеграции одного изображения с более высоким разрешением. ( a ) стерео с одним спутником, ( b ) стерео с одним спутником + одно изображение с более высоким разрешением.
Рисунок 4. Тестовые случаи для сравнения до и после интеграции одного изображения с более высоким разрешением.( a ) стерео с одним спутником, ( b ) стерео с одним спутником + одно изображение с более высоким разрешением.
Рисунок 5. Тестовые случаи для сравнения до и после интеграции стереоизображения с более высоким разрешением. ( a ) односпутниковое стерео, ( b ) односпутниковое стерео + стереоизображение более высокого разрешения.
Рисунок 5. Тестовые случаи для сравнения до и после интеграции стереоизображения с более высоким разрешением.( a ) односпутниковое стерео, ( b ) односпутниковое стерео + стереоизображение более высокого разрешения.
4. Экспериментальные результаты
Используя изображения IKONOS, QuickBird и KOMPSAT-2, мы провели различные интеграции, используя несколько спутниковых изображений, и проанализировали их конвергенцию, углы BIE и точность позиционирования. Точность оценивалась путем сравнения с 18 ICP после определения трехмерных наземных точек для каждой пары интегрирования. В Таблице 3 и Таблице 4 представлена точность каждой пары интегрирования с использованием среднеквадратичной ошибки (RMSE).Эти результаты в основном сравнивались с результатами трех стереопар с одним спутником, показанных в таблице 2. Точность позиционирования стереопар с одним спутником хорошо объяснялась разрешением изображения или расстоянием выборки на местности.Таблица 2. Точность отображения односпутниковых стереоизображений.
| Угол схождения | Угол БИЭ | Точность по горизонтали | Точность по вертикали | ||||
|---|---|---|---|---|---|---|---|
| Стерео | КОМПСАТ-27 ° | 89.3 ° | 89.3 ° | 2,15 м | 1.75 м | ||
| Ikonos Stereo | 35.0 ° | 75,5 ° | м | 0,86 м | |||
| Quickbird Stereo | 61.3 ° | 85.7 ° | 1,15 м | 0,63 м |
Таблица 3. Точность сопоставления двух разных спутниковых снимков.
| Изображение 1 | Изображение 2 | Угол конвергенции | Угол BIE | Горизонтальная точность | Вертикальная точность | ||
|---|---|---|---|---|---|---|---|
| K2-S1 | IK-S1 | 42,5 ° | 71,7 ° | 1,65 M | 2,74 м | ||
| K2-S1 | IK-S2 | IK-S2 | 52.9 ° | 83,9 ° | 83,9 ° | 1,78 м | 2,39 м |
| K2-S2 | IK-S1 | 26.1 ° | 74,8 ° 70071 | 1.86 M | 2.87 M | 2,87 м | |
| K2-S2 | IK-S2 | 8,90 ° | 71.6 ° | 3,87 м | 12.10 м | ||
| K2-S1 | qb-s1 | 53.2 ° | 53.2 ° | 73.2 ° | 1,88 м | 1,65 м | |
| K2-S2 | QB-S2 | 25.3 ° | 69,4 ° | 1,83 м | 2,80 м | ||
| K2-s2 | QB-s1 | 36.9 ° | 64.0 ° | 64.0 ° | 2.71 м | 2,71 м | |
| K2-S2 | QB-S2 | qb-s2 | 39,1 ° | 75.7 ° | 1,51 м | 2,02 м | |
| IK-S1 | QB-S1 | 50.4 ° | 50.4 ° | 79.8 ° | 1,39 м | 1.07 M | |
| IK-S2 | QB-S2 | 14.5 ° | 63.2 ° | 2,80 м | 3,59 м | ||
| IK-s2 | QB-s1 | 17.6 ° | 65.1 ° | 65.1 ° | 1,95 м | 2,86 м | |
| IK-S2 | QB-S2 | 47,8 ° | 47,8 ° | 78.2 ° | 1,30 м | 1.54 M | |
| 153 |
В целом сравнения показали, что двухспутниковая интеграция может быть эффективной альтернативой для горизонтального картографирования, но в настоящее время имеет низкую точность вертикального картирования.Это верно даже для сценариев интеграции с достаточной конвергенцией и геометрией BIE.
Во-вторых, точность, достигнутая при использовании дополнительных изображений, представлена в Таблице 4. В верхней части Таблицы 4 показана точность, когда одиночное изображение с более высоким разрешением было интегрировано в односпутниковые стереоизображения. Каждый результат включает конвергенцию и углы BIE, созданные между всеми интегрированными изображениями. Первый случай – это интеграция стерео КОМПСАТ-2 и одиночных изображений IKONOS.Что касается общей точности, то стереосистема KOMPSAT-2 была улучшена за счет первой интеграции, но не за счет второй интеграции. Вероятно, это связано с тем, что между IKONOS scene-2 и KOMPSAT-2 scene-2 была создана очень слабая геометрия (например, угол схождения 8,90°). Это явление также можно наблюдать в третьем случае, когда объединены стереоизображения IKONOS и одиночные изображения QuickBird. Точность стерео IKONOS была улучшена как по горизонтали, так и по вертикали при первом интегрировании, но не при втором интегрировании, которое создало наименьшую конвергенцию (14.53°) и углы BIE (63,23°). Во втором случае (интеграция стерео KOMPSAT-2 и одиночного изображения QuickBird) и первая, и вторая интеграции QuickBird повысили точность стерео KOMPSAT-2. Эти две интеграции также показали влияние угла BIE. Хотя второе интегрирование имеет преимущество с точки зрения общих углов сходимости, повышение точности первого интегрирования, которое включает наименьший угол BIE, было меньше, чем у второго интегрирования. В целом, результаты показывают, что дополнительное одиночное изображение с более высоким разрешением может повысить точность существующего стереокартографирования за счет соответствующего выбора изображения с учетом конвергенции или углов BIE.Это указывает на то, что рассмотрение углов необходимо распространить на использование трех изображений, а также двух изображений. Однако, что еще более важно, избегание создания очень малых или слабых углов должно иметь более высокий приоритет, чем выбор пар с высокими средними углами.Таблица 4. Точность отображения трех и более спутниковых снимков.
Интеграция трех изображений (односпутниковая стерео + высшее разрешение одно изображение) 1 2 3 3 Угол конвергенции BIE Угол 9 вертикальная точность 1-2 6 QB-S16 IK-S16 QB-S24 интеграция четырех или нескольких изображений (односпутниковая стерео + высшее разрешение стерео) 1 3 4 1-2 1-3 1-42 K2-S22 K2-S12 QB-S2| горизонтальная точность | ||||||||||||||||||||||
| 1-3 | 2-3 | 1-2 | 1-3 | 2-3 | ||||||||||||||||||
| K2-s1 | K2-s2 | IK-s1 | 47.7 ° | 42.5 ° | 26.1 ° | 26.1 ° | 89.3 ° | 89.3 ° | 71.8 ° | 74,8 ° | 74,8 ° | 1,66 м | 1.65 м | |||||||||
| K2-S1 | K2-S2 | 47.7 ° | 52.0 ° | 89 ° | 89 ° | 89,3 ° | 83.9 ° | 83.9 ° | 71.6 ° | 1,72 м | 2,37 м | |||||||||||
| K2-S1 | K2-S2 | 47,7 ° | 53,2° | 36,9° | 89.3 ° | 73.1 ° | 73.1 ° | 64.0 ° | 1,56 м | 1.60 м | ||||||||||||
| K2-S1 | K2-S2 | QB-S2 | 47,7 ° | 25.3 ° | 39,1 ° | 89.3 ° | 69,4 ° | 75,7 ° | 75.7 ° | 1,43 м | 1,27 м | |||||||||||
| IK-S1 | IK-S2 | QB-S1 | 35.0 ° | 50,4 ° | 17,6 ° | 75,5 ° | 79,8° | 65,1° | 1.31 м | 0,70 м | 0,70 м | |||||||||||
| IK-S2 | QB-S2 | 35.0 ° | 14.5 ° | 47,8 ° | 75,5 ° | 63.2 ° | 78.2 ° | 1.65 M | 0,89 м | |||||||||||||
| 6 2 | Конвергенция Угол | МБВ Угол | Горизонтальная точность | Вертикальная точность | ||||||||||||||||||
| 1-2 | 1-3 1-3 | 1-4 | ||||||||||||||||||||
| 2-3 | 2-4 | 3-4 9007 1 | 2-3 | 2-3 | 2-4 | 3-4 | ||||||||||||||||
| K2-S2 | IK-S1 | IK-S2 | 47.7 ° | 42.5 ° | 52.0 ° | 52.0 ° | 89.3 ° | 71.9 ° | 71.9 ° | 83.9 ° | 1.62 м | 0 1.45 м | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 26.1 ° | 8.90 ° | 35,0 ° | 74,8 ° | 71.6 ° | 75.5 ° | 75.5 ° | ||||||||||||||||
| K2-S2 | QB-S1 | QB-S2 | 47,7 ° | 53.2 ° | 25.3 ° | 89.3 ° | 73.2 ° | 69,4° | 1,37 м | 0.92 м | ||||||||||||
| 36.9 ° | 39,1 ° | 39,1 ° | 61.3 ° | 64.0 ° | 64.7 ° | 75.7 ° | 85.7 ° | |||||||||||||||
| IK-S1 | IK-S2 | QB-S2 | QB-S2 | 35.0 ° | 50.0 ° | 50.4 ° | 14.5 ° | 75.5 ° | 75.5 ° | 75.5 ° | 79,8 ° | 63.2 ° | 0 1,21 м | 0 0,65 м | ||||||||
| 17.6 ° | 47,8 ° | 61.3 ° | 65,1 ° | 78,2° | 85.7 ° | |||||||||||||||||
| Интеграция всех изображений (три стереопары) | ||||||||||||||||||||||
| Конвергенция Угол | МБВ Angle | Горизонтальная точность | Вертикальная точность | |||||||||||||||||||
| K2stereo + IKstereo + QBstereo | — | — | 1,35 м | 0,68 м | ||||||||||||||||||
Наш анализ показывает, что соответствующая интеграция изображений с более высоким разрешением может быть очень эффективной для повышения точности существующих стереоизображений. Мы также отмечаем, что существуют различия между интеграцией с использованием одного изображения и интеграцией с использованием стереоизображения.При интеграции изображений с более высоким разрешением в существующие стереопары: добавление одного изображения может снизить точность, если изображение создает очень слабую конвергенцию или угол BIE с любым из существующих стереоизображений, тогда как интеграция стереоизображения не снижает точность.
Между тем, в дополнение к обнаружению того, что очень слабая конвергенция или угол BIE могут снизить точность, для реальных картографических приложений может потребоваться более конкретное определение слабой геометрии. Тем не менее, такую слабую геометрию трудно четко определить, и это остается сложной проблемой в этой области.На основании результатов, приведенных в Таблице 4, пользователям дистанционного зондирования рекомендуется избегать интеграции одного изображения, которое создает угол конвергенции менее 20° и угол BIE менее 70°.В этом разделе точность геопозиционирования с использованием нескольких спутниковых изображений была проанализирована по сравнению с точностью с использованием обычных стереоизображений с одного датчика. В целом, интеграция с двумя датчиками обеспечила ожидаемое повышение точности в горизонтальном направлении, но показала худшие результаты, чем ожидалось, в вертикальном направлении.Наши результаты также показывают, что интеграция нескольких спутниковых изображений может улучшить традиционные односпутниковые модели за счет соответствующего использования изображений с более высоким разрешением.
5. Обсуждение
Как было предложено ранее, для картографирования на основе двухспутниковой интеграции точность по горизонтали соответствовала ожиданиям, основанным на разрешении изображения, если только не была создана очень слабая геометрия, но результирующая точность по вертикали противоречила таким ожиданиям. В частности, вертикальные ошибки были больше, чем у односпутниковых стереопар, даже в тех случаях, когда геометрическая стабильность сравнима со стереоизображениями с одного спутника, а среднее разрешение в среднем выше, чем у односпутниковых стереоизображений.В этом разделе обсуждается основной источник этого явления.
Как показано на рис. 6, геопозиционирование с использованием стереопар выполняется путем достижения точки трехмерного пересечения G S , оцененной с использованием двух лучей. На левой панели, если два луча не имеют ошибок (безошибочный сценарий представлен пунктирными линиями), два луча пересекутся точно в истинной точке земли G T . Однако лучи обычно имеют отдельные ошибки наведения (обозначенные на средней панели как GTG1→ и GTG2→), которые создают горизонтальные и вертикальные ошибки в объектном пространстве.G 1 и G 2 являются точками пересечения двух лучей сцены-1 и сцены-2 соответственно с горизонтальной плоскостью, содержащей G T . Отдельные ошибки наведения были ранее представлены для описания горизонтальных и вертикальных ошибок [13], но их взаимосвязь не обсуждалась. Здесь мы обсудим, как ошибки наведения связаны с горизонтальной и вертикальной точностью, как показано на рисунке 6.Рисунок 6. Взаимосвязь между векторами ошибок наведения отдельного изображения и ошибками 3D-позиционирования.
Рисунок 6. Взаимосвязь между векторами ошибок наведения отдельного изображения и ошибками 3D-позиционирования.
На средней панели рисунка 6 показано, что горизонтальная ошибка в основном зависит от величины суммы двух векторов ошибок |GTG1→+GTG2→|, которые обычно пропорциональны разрешению отдельного используемого изображения. Эта интерпретация подтверждает наше наблюдение, что горизонтальные ошибки хорошо объясняются разрешением изображения. С другой стороны, правая панель показывает, что вертикальная ошибка может быть выражена как функция угла конвергенции и |GTG1→-GTG2→|, которая получается путем вычитания двух векторов ошибок.Величина вектора вычитания зависит от корреляции или сходства шаблона между двумя векторами ошибок. Например, более похожие шаблоны приводят к большей величине вектора вычитания. Корреляция между углом сходимости и вертикальной ошибкой была предложена ранее [11,14]. В этой статье предполагается, что сходство шаблонов ошибок наведения между стереоизображениями также сильно коррелирует с вертикальной ошибкой. Это объясняет, почему вертикальную ошибку нельзя объяснить разрешением изображения.Вертикальная ошибка, в отличие от горизонтальной ошибки, тесно связана не с величиной векторов ошибок, а скорее с их корреляцией или сходством. Эмпирически было установлено, что такое сходство ошибок наведения существенно различается между односпутниковой стереосистемой и двухспутниковой интеграцией. . На рисунке 7 показаны отдельные ошибки наведения используемых изображений для пяти ICP. На рис. 7а показаны результаты двух снимков КОМПСАТ-2 и двух изображений IKONOS. Модели ошибок наведения между двумя изображениями КОМПСАТ-2 или между двумя изображениями IKONOS очень похожи.Однако характер ошибок наведения сильно отличался между одним изображением КОМПСАТ-2 и одним изображением IKONOS. Таким образом, расстояния между концами вектора ошибки наведения, называемые величиной вектора вычитания |GTG1→−GTG2→|, при интеграции КОМПСАТ-2/ИКОНОС были больше, чем при объединении двух изображений КОМПСАТ-2, а также двух изображений ИКОНОС. . Это привело к неожиданно низкой вертикальной точности интеграции КОМПСАТ-2/ИКОНОС, которая даже ниже, чем у стереопары КОМПСАТ-2. На рис. 7b представлены ошибки наведения двух изображений KOMPSAT-2 и двух изображений QuickBird, а на рисунке 7c — двух изображений IKONOS и двух изображений QuickBird.Эти два случая также дали результаты, аналогичные описанным. В целом, модели ошибок наведения одного и того же спутника были очень похожими, тогда как ошибки разных спутников сильно отличались; следовательно, вычитающий вектор с большей величиной приводит к большей вертикальной ошибке из-за двухспутниковой интеграции.Рисунок 7. Векторы ошибок наведения и векторы их вычитания для односпутникового стерео и двухспутникового стерео (пять ICP). ( a ) КОМПСАТ-2/IKONOS, ( b ) КОМПСАТ-2/QuickBird, ( c ) IKONOS/QuickBird.
Рис. 7. Векторы ошибок наведения и векторы их вычитания для односпутникового стерео и двухспутникового стерео (пять ICP). ( a ) КОМПСАТ-2/IKONOS, ( b ) КОМПСАТ-2/QuickBird, ( c ) IKONOS/QuickBird.
В таблице 5 показан количественный анализ с использованием всех 18 ICP. Используя координаты концов вектора ошибки, были рассчитаны коэффициенты корреляции и величины вектора вычитания между двумя векторами ошибки. Таблица очень хорошо поддерживает наш визуальный анализ и интерпретацию.Корреляции (подобие) двухспутниковых интеграций были очень низкими, а их векторные величины вычитания были очень большими по сравнению с тремя односпутниковыми стереопарами.В этом разделе показано, что сходство или несходство шаблонов между отдельными ошибками наведения является важным фактором для точности картирования при использовании двух спутниковых изображений. Полученные данные показывают, что интеграция с двумя спутниками может не обеспечивать достаточную точность для картирования вертикального положения, и показывают, что основной причиной этого явления было несходство моделей ошибок между двумя разными спутниковыми изображениями.Однако это явление четко не наблюдается при объединении трех и более изображений. Мы продолжим рассмотрение таких сценариев в будущих исследованиях по другой важной теме.
Таблица 5. Сходство шаблонов ошибок наведения для односпутникового стерео и двухспутникового стерео (18 ICP).
| Изображение 1 | Изображение 2 | Корреляция | |GTG1→−GTG2→| | ||
|---|---|---|---|---|---|
| Односпутниковые стереопары | K2-s1 | K2-s2 | 0.651 | 1.26 M | 1,26 м |
| IK-S1 | IK-S2 | 0.810 | 0.69 M | ||
| QB-S1 | QB-S2 | 0.760 | 0,83 м | ||
| Dual-Satellite Интеграции | K2-S1 | IK-S1 | 0.256 | 1,92 м | |
| K2-S1 | IK-S2 | 0.213 | 2.11 M | ||
| K2-S2 | IK-S1 | 0,292 | 1.75 м | ||
| K2-S2 | IK-S2 | 0.310 | 1.69 M | 1,69 м | |
| K2-S1 | QB-S1 | 0.233 | 2,25 м | ||
| K2-S1 | QB -s2 | 0.320 | 0.320 | 2.16 M | |
| K2-S2 | QB-S1 | 0.342 | 1.83 M | ||
| K2-S2 | QB-S2 | 0.370 | 1,91 м | ||
| IK-s1 | QB-s1 | 0.351 | 1.63 M | 1,63 м | |
| IK-S1 | QB-S2 | 0.392 | 1,57 м | ||
| IK-S2 | QB-S1 | 0.311 | 1,81 м | ||
| IK-S2 | QB-s2 | 0,345 | 1,60 м |
чтобы проверить пригодность для реальных картографических приложений.Наш анализ показал, что двухспутниковая интеграция может быть эффективной при картографировании горизонтального положения, но имеет некоторые ограничения при картографировании вертикального положения. Было обнаружено, что основным источником такого ограничения является несходство моделей ошибок наведения на двух разных спутниковых изображениях. Наш анализ также показал, что интеграция дополнительных изображений с более высоким разрешением может повысить общую точность существующих односпутниковых стереоизображений. В этом приложении интеграция одного изображения должна выполняться очень осторожно, проверяя, создает ли интеграция очень слабую конвергенцию или углы BIE, в то время как интеграция стереоизображений всегда должна быть одобрена.В целом, наше исследование подтвердило, что надлежащее использование нескольких спутниковых изображений может быть эффективным для геопозиционирования. И наоборот, также было обнаружено, что, в отличие от обычных стереоданных, более высокое разрешение не является обязательным условием для точного картографирования, и поэтому при обработке данных с нескольких спутников необходимо учитывать различные геометрические элементы. Мы надеемся, что наши результаты помогут улучшить понимание использования изображений с нескольких спутников и предложить рекомендации по эффективному использованию спутниковых изображений в реальных картографических приложениях.
ВЗАИМОДЕЙСТВИЕ МЕЖДУ УГЛОМ СХОДА, НАГРУЗКОЙ ДВИЖЕНИЯ И ВЫСОТОЙ DIS
РЕФЕРАТ Прошлые исследования показывают, что способность авиадиспетчеров определять, пролетят ли два самолета-мишени слишком близко друг к другу опосредуется углом схождения между ними: более широкие углы схождения связаны с ухудшенным обнаружением конфликтов (особенно при высокой транспортной нагрузке), из-за большего необходимого количества визуальных сканирование. Мы попытались обобщить эти результаты на более экологически обоснованных дисплеях (а) с большей высотой. распределения, чем те, которые использовались в предыдущих исследованиях; и (b) когда контролеры не могли быть уверены в существовании конфликта на каждом испытании.Четырнадцать авиадиспетчеров выполнили стандартную задачу по обнаружению конфликтов, в ходе которой оба систематически изменялись угол схождения и транспортная нагрузка. Хотя мы наблюдали большое влияние трафика нагрузку как на точность, так и на время отклика, угол сходимости не влиял на производительность даже при высоких нагрузках. Таким образом угол сходимости может играть лишь ограниченную роль в посредничестве диспетчеров в обнаружении конфликтов во многих случаях. отображение фактического воздушного движения. Ключевые слова: управление воздушным движением; визуальное сканирование; угол схождения; обнаружение конфликтов ВВЕДЕНИЕ Авиадиспетчеры обеспечивают безопасное, упорядоченное и оперативное движение в национальном воздушном пространстве. система.Предоставление этой услуги в значительной степени зависит от способности контролера экстраполировать траектории самолетов от их текущего положения к будущей точке, а затем пространственно определить, будет ли их расстояние в ближайшей точке сближения нарушает требование о минимальном эшелонировании. Если да, то конфликт существуют. На способность диспетчера обнаруживать конфликты, в свою очередь, влияет множество факторов, которые включают (но не ограничивается) интенсивностью движения, типом воздушного судна, географическим положением воздушного пространства, размером сектора и углом схождения.Здесь мы фокусируемся в первую очередь на роль, которую угол схождения двух самолетов может или не может играть в посредничестве конфликта обнаружение. Возможная важность угла конвергенции в этом контексте подсказывает интуиция, предыдущие исследования в других областях, а также анекдотические аспекты заметных неудач обнаружения конфликтов в реальном мире. Интуитивно кажется вероятным, что больший угол схождения двух самолетов приведет к большим трудностям в определение вероятности конфликта между ними.Эта интуиция основана прежде всего на необходимом шаге сканирование между двумя самолетами для обнаружения конфликта (например, Bisseret, 1981): более широкие углы схождения будут увеличить время и расстояние этого сканирования и часто может привести к обнаружению большего количества вмешивающихся самолет-дистрактор. В результате кажется естественным ожидать, что большие углы сходимости могут привести к обнаружению конфликтов. ухудшения с точки зрения времени отклика и точности. Такие прогнозы также подтверждаются эмпирическими исследованиями. роли углов конвергенции в других контекстах, которые не должны напрямую включать обнаружение конфликтов.Например, более широкие углы сходимости заставляют испытуемых занимать больше времени при простой экстраполяции траекторий (например, Смита, Эллиса и т. д.). Ли, 1984).
Индивидуальное прогнозирование угла конвергенции линии сустава после высокой остеотомии большеберцовой кости с использованием рентгенограммы всей ноги в положении стоя на латеральной клиновидной стельке рентгенограмма всей ноги в положении стоя на клиновидной стельке
AU — Акасаки, Юкио
AU — Мидзу-ути, Хидэки
AU — Хамаи, Сатоши
AU — Цусима, Хидетоши
, Шинхара — Кава AU — Horikawa, Tomohiro
AU — Nakashima, Yasuharu
N1 — Авторские права издателя: © 2019, Европейское общество спортивной травматологии, хирургии коленного сустава, артроскопии (ESSKA).
PY — 2020/10/1
Y1 — 2020/10/1
N2 — Цель: оценить полезность рентгенограммы всей ноги, стоящей на латеральной клиновидной стельке (LWI), для прогнозирования изменения линии сустава угол конвергенции (JLCA) до и после высокой остеотомии большеберцовой кости (HTO). Методы: 40 коленных суставов с медиальным остеоартрозом подверглись открытой клиновидной ВТО. Перед операцией всем пациентам были сделаны рентгенограммы всей ноги в трех различных состояниях: лежа на спине, стоя и стоя на LWI под углом 20°.После операции также была сделана рентгенограмма всей ноги в положении стоя. Сравнивали радиологические измерения, включая JLCA и процент механической оси (% MA). Используя предоперационные рентгенограммы, были рассчитаны углы коррекции с целевым значением %MA 62,5%. Были оценены корреляции между разницей в рассчитанном угле коррекции между тремя предоперационными состояниями и изменением JLCA до и после ВТО. Результаты. В предоперационном положении стоя средний JLCA с 3,8° значительно снизился до 3.2° с использованием LWI, что не отличалось от послеоперационного JLCA 3,1°. Среднее значение %MA значительно сместилось латерально с 20,6 до 24,8% при использовании LWI и сильно коррелировало с изменением JLCA (коэффициент 0,83). Вычисленные углы коррекции значительно различались в трех дооперационных условиях. Разница в рассчитанном угле коррекции между стоянием с LWI и без него сильно коррелировала с изменением JLCA стоя до и после HTO (коэффициент 0,73). Вывод: большие различия в рассчитанных углах коррекции между дооперационными рентгенограммами в положении стоя с LWI и без LWI предсказывали большие изменения JLCA после HTO.Рентгенограмма всей ноги в положении стоя на LWI является многообещающим методом для правильного предоперационного планирования с учетом специфических для пациента изменений JLCA до и после HTO. Уровень доказательности: IV.
AB — Цель: оценить полезность рентгенограммы всей ноги в положении стоя на стельке с латеральным клином (LWI) для прогнозирования изменения угла конвергенции линии сустава (JLCA) до и после высокой остеотомии большеберцовой кости (HTO). Методы: 40 коленных суставов с медиальным остеоартрозом подверглись открытой клиновидной ВТО. Перед операцией всем пациентам были сделаны рентгенограммы всей ноги в трех различных состояниях: лежа на спине, стоя и стоя на LWI под углом 20°.После операции также была сделана рентгенограмма всей ноги в положении стоя. Сравнивали радиологические измерения, включая JLCA и процент механической оси (% MA). Используя предоперационные рентгенограммы, были рассчитаны углы коррекции с целевым значением %MA 62,5%. Были оценены корреляции между разницей в рассчитанном угле коррекции между тремя предоперационными состояниями и изменением JLCA до и после ВТО. Результаты. В предоперационном положении стоя средний JLCA с 3,8° значительно снизился до 3.2° с использованием LWI, что не отличалось от послеоперационного JLCA 3,1°. Среднее значение %MA значительно сместилось латерально с 20,6 до 24,8% при использовании LWI и сильно коррелировало с изменением JLCA (коэффициент 0,83). Вычисленные углы коррекции значительно различались в трех дооперационных условиях. Разница в рассчитанном угле коррекции между стоянием с LWI и без него сильно коррелировала с изменением JLCA стоя до и после HTO (коэффициент 0,73). Вывод: большие различия в рассчитанных углах коррекции между дооперационными рентгенограммами в положении стоя с LWI и без LWI предсказывали большие изменения JLCA после HTO.Рентгенограмма всей ноги в положении стоя на LWI является многообещающим методом для правильного предоперационного планирования с учетом специфических для пациента изменений JLCA до и после HTO. Уровень доказательности: IV.
UR — http://www.scopus.com/inward/record.url?scp=85076841458&partnerID=8YFLogxK
UR — http://www.scopus.com/inward/citedby.url?scp=85076841458&partnerID=8YFLogxK
U2 — 10.1007 / S00167-019-05821-8
DO — 10.1007 / S00167-019-05821-8
м3 — Статья
C2 — 31828362
AN — Scopus: 85076841458
VL — 28
SP — 3200
EP — 3206
EP — 3206
Джо — операция на коленях, спортивная травматология, артроскопия
JF — операция на коленях, спортивная травматология, артроскопия
SN — 0942-2056
IS — 10
ER —
Концепции of Stereo Vision
Концепции Stereo VisionЕсть два основных фактора для создания трехмерного стереоизображения: Convergence и Parallax .
Конвергенция
Конвергенция — это угол, образованный вашими глазами и наблюдаемым объектом. Чем выше значение угла, тем ближе наблюдаемый объект к вашим двум глаза, и наоборот.
Высокая сходимость (целевой объект рядом) | Низкая сходимость (целевой объект далеко) |
Поэтому, когда конвергенция зафиксирована, любой объект между вами и точкой конвергенции будет ближе к вам, а объект за точкой конвергенции будет дальше от вас.
Обратите внимание, что если Convergence выше 6 градусов, это означает, что объект находится слишком близко к вы, то ваши глаза чувствуют себя неловко. Напротив, когда значение слишком мало, что означает, что объект находится слишком далеко, стерео ощущение будет Потерянный.
Параллакс
Изображения параллакса — это изображения, проходящие через ваш левый и правый глаза. Все 3D-стерео носители содержат пару изображений параллакса. которые по отдельности и одновременно проходят к вашим левому и правому глазу.Это нужно для того, чтобы убедить ваш мозг в том, что в средствах массовой информации существует глубина.
Положительный параллакс
Когда целевой объект смещается вправо на левом изображении и смещается слева на правом изображении, то ваш бинокулярный фокус приводит к отставанию от отображать. Это явление называется Положительный Параллакс .
Ваша точка схождения ведет к отставанию дисплей. | Положительный параллакс |
Нулевой параллакс
Когда парные изображения параллакса накладываются на дисплей, ваш бинокулярный фокус приводит к падению на тот же дисплей, который является Нулевой параллакс .
Изображение L и R ведет к вашей конвергенции точку, чтобы попасть на дисплей. | Нулевой параллакс |
Отрицательный параллакс
Когда целевой объект смещается влево на левом изображении и смещается вправо на правом изображении, то ваш бинокулярный фокус приводит к падению перед дисплей. Это явление называется Отрицательный Параллакс .
Изображения L и R ведут к вашей конвергенции точку, чтобы упасть перед дисплеем. | Отрицательный параллакс |
Экспериментальное и численное исследование влияния угла схождения, давления впрыска и числа впрысков на тепловые характеристики прямой вихревой трубы
[1] Рафи С.Е., Садегиазад М.М. (2016). Тепломассоперенос между холодным и горячим ядрами вихря внутри вихревой трубы Ранка-Хилша — оптимизация длины горячей трубы, International Journal of Heat and Technology, Vol.34, № 1, стр. 31-38. DOI: 10.18280/ijht.340105
[2] Багдад М., Уадха А., Имин О., Аддад Ю. (2011). Численное исследование разделения энергии в вихревой трубе с использованием различных моделей RANS, Межд. J. Тепловые науки, Vol. 50, № 12, стр. 2377-2385. DOI: 10.1016/j.ijthermalsci.2011.07.011
[3] Рафи С.Е., Садегиазад М.М. (2016). Трехмерное компьютерное предсказание явления отрыва вихря внутри вихревой трубы Ранка-Хилша, Авиация, Том. 20, № 1, с. 21-31 DOI: 10.3846/16487788.2016.1139814
[4] Guo Q., Qi X., Wei Z., Guo P., Sun P. (2016). Трехмерное численное моделирование и анализ холодильных характеристик вихревой трубы малого диаметра, International Journal of Heat and Technology, Vol. 34, № 3, стр. 513-520. DOI: 10.18280/ijht.340324
[5] Пурмахмуд Н., Аббасзаде М., Рашидзаде М. (2016). Численное моделирование влияния теплообмена оболочки на характеристики вихревой трубы, International Journal of Heat and Technology, Vol. 34, нет.2, стр. 293-301. DOI: 10.18280/ijht.340220
[6] Пурмахмуд Н., Эсмаили Р., Хассанзаде А. (2015). CFD исследование влияния длины вихревой трубы как критерия проектирования, International Journal of Heat and Technology, Vol. 33, № 1, стр. 129-136. DOI: 10.18280/ijht.330118
[7] Рахими М., Рафи С.Е., Пурмахмуд Н. (2013). Численное исследование влияния расширяющейся горячей трубы на разделение энергии в вихревой трубе, International Journal of Heat and Technology, Vol.31, № 2, стр. 17-26.
[8] Рафи С.Э., Рахими М., Пурмахмуд Н. (2013). Трехмерное численное исследование коммерческой вихревой трубы на основе экспериментальной модели — Часть I: оптимизация радиуса рабочей трубы, International Journal of Heat and Technology, Vol. 31, № 1, стр. 49-56.
[9] Рафи С.Э., Садегиазад М.М. (2015). Трехмерный численный анализ влияния скругления радиуса кромки на тепловое разделение внутри вихревой трубы, International Journal of Heat and Technology, Vol.33, № 1, стр. 83-90.
[10] Пурмахмуд Н., Хасанзаде А., Рафи С.Э., Рахими М. (2012). Трехмерное численное исследование влияния сужающихся сопел на энергоразделение в вихревой трубе, International Journal of Heat and Technology, Vol. 30, № 2, стр. 133-140.
[11] Пурмахмуд Н., Рафи С.Э., Рахими М., Хасанзаде А. (2013). Численный анализ разделения энергии на коммерческой вихревой трубе Ранка-Хилша на основе применения различных газов, Scientia Iranica., Том. 20, № 5, стр. 1528-1537.
[12] Хан С., Ли Н., Ву К., Ван З., Тан Л., Чен Г., Сюй С. (2013). Влияние характеристик рабочего газа на энергоразделение вихревой трубы // Прикладная теплотехника. 61, № 2, стр. 171-177. DOI: 10.1016/j.applthermaleng.2013.07.027
[13] Рафи С.Э., Садегиазад М.М., (2016). Трехмерное численное исследование процесса сепарации внутри вихревой трубы с использованием различных рабочих условий, Journal of Marine Science and Application, стр.1-10. DOI: 10.1007/s11804-016-1348-8
[14] Рафи С.Э., Садегиазад М.М. (2014). Эффект конический. угол клапана от температуры холодного выхода вихревой трубы, Журнал теплофизики и теплообмена, Vol. 28, стр. 785-794. DOI: 10.2514/1.T4376
[15] Рафи С.Э., Садегиазад М.М. (2014). Трехмерное и экспериментальное исследование влияния длины конуса дроссельной заслонки на тепловые характеристики вихревой трубы с использованием модели турбулентности k–ɛ, Прикладная теплотехника, Том.66, № 1-2, стр. 65-74. DOI: 10.1016/j.applthermaleng.2014.01.073
[16] Рафи С.Е., Садегиазад М.М., Мостафавиния Н. (2013). Экспериментальное и численное исследование влияния угла схождения и диаметра холодного отверстия на тепловые характеристики сужающейся вихревой трубы, J. Thermal Sci. англ. Заявл., Том. 7, No. 4. DOI: 10.1115/1.4030639
[17] Рафи С.Э., Садегиазад М.М. (2014). Трехмерный CFD эксергетический анализ характеристик противоточной вихревой трубы, International Journal of Heat and Technology, Vol.32, № 1-2, стр. 71-77.
[18] Рафи С.Э., Рахими М. (2014). Трехмерное моделирование течения жидкости и разделения энергии внутри вихревой трубы, Журнал теплофизики и теплопередачи, Vol. 28, стр. 87-99. DOI: 10.2514/1.T4198
[19] Лоренцини Э., Спига М. (1982). Аспетти флюидодинамические делла сепарационе изотопика медианте трубы и вихря Хилш Ingegneria, № 5-6, стр. 121-126.
KoreaMed Synapse
1. Словарь ортопедических терминов. Джей Простет Дент.2005 г.; 94:10–92.
2. Йоргенсен К.Д. Взаимосвязь между ретенцией и углом конвергенции в коронках из цементных виниров. Акта Одонтол Сканд. 1955 год; 13:35–40.
3. Кауфман Э.Г., Коэльо Д.Х., Колин Л. Факторы, влияющие на удержание цементированных золотых отливок. Джей Простет Дент. 1961 год; 11: 487–502.
4. Goodacre CJ, Campagni WV, Aquilino SA. Препарирование зубов под полные коронки: форма искусства, основанная на научных принципах. Джей Простет Дент. 2001 г.; 85:363–376.
5. Уилсон А.Х. младший, Чан Д.К. Взаимосвязь между конвергенцией препарирования и удержанием внекоронковых фиксаторов. Дж. Протез. 1994 год; 3:74–78.
6. Сорняк РМ. Определение адекватной конвергенции коронки. Текс Дент Дж. 1980; 98:14–16.
7. Аль-Омари В.М., Аль-Вахадни А.М. Угол конвергенции, окклюзионная редукция и глубина финишной линии препарирования полной коронки, сделанные студентами-стоматологами. Квинтэссенция Инт. 2004 г.; 35:287–293.
8. Эль-Эбраши М.К., Крейг Р.Г., Пейтон Ф.А.Экспериментальный стресс-анализ зубных реставраций. VI. Концепция проксимальной репозиции в составных реставрациях. Джей Простет Дент. 1969 год; 22:663–670.
9. Виид Р.М., Баэз Р.Дж. Способ определения адекватной формы резистентности полных литых препаровок под коронки. Джей Простет Дент. 1984 год; 52:330–334.
10. Льюис Р.М., Оуэн М.М. Математическое решение задачи построения полной коронки. J Am Dent Assoc. 1959 год; 59:943–947.
11. Шиллингбург Х.Т., Хобо С., Уитсетт Л.Д., Брэкетт С.Е.Основы несъемного протезирования. В: Бейтман Л.А., редактор. Принципы препарирования зубов. 3-е изд. Чикаго: паб Quintessence. Ко; 1997. п. 119–138.
12. Чандра Шекар С., Гиридхар К., Сухас Рао К. Исследование in vitro для оценки ретенции полных коронок, изготовленных с использованием пяти различных конусов и зафиксированных двумя разными цементами. J Индийский протез Soc. 2010 г.; 10:89–95.
13. Аннерштедт А., Энгстрем У., Ханссон А., Янссон Т., Карлссон С., Лильхаген Х., Линдквист Э., Ридхаммар Э., Тайреман-Бандхеде М., Свенссон П., Вандел У.Аксиальная конвергенция стенок полных облицовочных коронок. Документировано для студентов-стоматологов и врачей общей практики. Акта Одонтол Сканд. 1996 год; 54:109–112.
14. Мак П.Дж. Теоретическое и клиническое исследование конусности при препарировании коронок и вкладок. J Оральная реабилитация. 1980 г.; 7: 255–265.
15. Ом Э., Силнесс Дж. Угол конвергенции зубов, препарированных под искусственные коронки. J Оральная реабилитация. 1978 год; 5: 371–375.
16. Leempoel PJ, Lemmens PL, Snoek PA, van’t Hof MA.Угол конвергенции препарирования зубов под полные коронки. Джей Простет Дент. 1987 год; 58:414–416.
17. Smith CT, Gary JJ, Conkin JE, Franks HL. Эффективный критерий конусности для полной облицовки коронки в доклиническом протезировании. Дж. Протез. 1999 г.; 8: 196–200.
18. Веласкес-Плата Д., Андрес С.Дж. Искусство подготовки коронки: обзор принципов. Дж. Индиана Дент, доц. 1996 год; 75:6–11.
19. Аяд М.Ф., Маграби А.А., Розенстил С.Ф.Оценка углов конвергенции препарирования зубов под полные коронки у студентов-стоматологов. Джей Дент. 2005 г.; 33:633–638.
20. Dodge WW, Weed RM, Baez RJ, Buchanan RN. Влияние угла конвергенции на форму ретенции и сопротивления. Квинтэссенция Инт. 1985 год; 16:191–194.
21. Нордландер Дж., Вейр Д., Стоффер В., Очи С. Сужение клинических препаратов для несъемного протезирования. Джей Простет Дент. 1988 год; 60:148–151.
22. Noonan JE Jr, Goldfogel MH.Конвергенция аксиальных стенок полных облицовочных коронок в условиях стоматологической школы. Джей Простет Дент. 1991 год; 66: 706–708.
23. Кент В.А., Шиллингбург Х.Т. мл., Дункансон М.Г. мл. Конусность клинических препаратов для литых реставраций. Квинтэссенция Инт. 1988 год; 19: 339–345.
24. Окуяма Ю., Касахара С., Кимура К. Количественная оценка осевой конусности стенок препарированных искусственных зубов. J Устные науки. 2005 г.; 47:129–133.
25. Дорриз Х., Нокар С., Багхай Наини Р., Мадади А.Угол конвергенции при препарировании коронок с полным покрытием, сделанных студентами-стоматологами. Джей Дент (Тегеран). 2008 г.; 5:37–41.
26. де Вет Х.К., Терви К.Б., Кнол Д.Л., Баутер Л.М. Когда использовать показатели согласия и надежности. Дж. Клин Эпидемиол. 2006 г.; 59:1033–1039.
27. Shrout PE, Fleiss JL. Внутриклассовые корреляции: использование при оценке надежности оценщиков.
