Расчет контуров в каталоге программного обеспечения на QRZ.RU

Программа опубликована К. Шульгиным (UA3DA) в журнале Радио No 11 за 1991 год для компьютеров типа «Радио-86РК» на языке basic.

Предлагаемый вариант программы представляет собой оригинал переведенный на современный язык программи- рования и скомпилированный для OS Windows и Linux. Программа работает в терминальном режиме. Дробные числа можно вводить через точку или запятую, результаты работы программы выводятся на экран, а так же, в режиме накопления (добавления данных) записываются в текстовый файл pi_data.txt с указанием даты расчета.

Программа производит расчет элементов П-контура, его параметров, а так же режима работы выходной цепи электронной лампы или транзистора. Для удобства работы ввод и вывод сделан с указанием наименования каждого из параметров (в эпоху компьютеров «Радио-86РК» в связи с жесткими ограничениями объемов памяти приходилось делать множество сокращений).

Запуск программы в OS Windows

Запуск программы в ОС Windows осуществляется bat файлом с именем start.

Для правильного отображения кодировки в окне терминала нужно установить шрифт терминала «Lucida Console» (это достаточно сделать только 1 раз), для этого:

1. запустите консоль windows (cmd.exe)
2. кликните правой кнопкой мыши на заголовок окна консоли и из меню выберите пункт «Свойства»;
3. во вкладке «Шрифт» примените шрифт на «Lucida Console»

Запуск программы в OS Linux

Запуск программы в ОС Linux осуществляется командой ./Pi_kontur (с точкой перед слешем). Для запуска программы необходимо, чтобы терминал был открыт в папке с файлом Pi_kontur, для этого:

1. перейдите проводником Linux в папку с файлом программы
2. по правому клику мыши вызовите контекстное меню,
3. выберите пункт «Открыть в терминале».

Калькулятор импеданса последовательной RLC-цепи, Электротехнические и радиотехнические калькуляторы, Конвертер величин

Калькулятор определяет импеданс и фазовый сдвиг для соединенных последовательно резистора, катушки индуктивности и конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота.

Пример. Рассчитать импеданс катушки индуктивности 1 Гн, конденсатора 100 мкФ и резистора 100 Ом на частоте 16 Гц. Калькулятор показывает импеданс около 100,006 Ом. Это почти резонанс. Можно проверить импеданс при почти полном резонансе, если ввести 15,9154 Гц вместо 16 Гц. При этой частоте импеданс получается емкостным. Однако, если ввести емкость чуть большую частоту 15,9155 Гц, импеданс станет индуктивным и вы увидите, что фазовый угол, который был чуть меньше нуля, стал положительным.

Входные данные

Сопротивление, R

миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)

Индуктивность, L

генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)

Емкость, С

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Частота, f

герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)

Выходные данные

Угловая частота ω= рад/с

Емкостное реактивное сопротивление X_C= Ом

Емкостное реактивное сопротивление X_L= Ом

Полный импеданс RLC |Z_RLC|= Ом

Фазовый сдвигφ = ° = рад

Добротность Q=

Резонансная частота

f₀=   Гц   ω₀=   рад/с

Введите значения сопротивления, емкости, индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.

Для расчетов используются указанные ниже формулы:

φ = 90° если 1/2πfC < 2πfL и R = 0

φ = –90° если 1/2πfC > 2πfL и R = 0

φ = 0° если 1/2πfC = 2πfL и R = 0

Здесь

Z_LC — импеданс цепи LC в омах (Ом),

ω = 2πf — угловая частота в рад/с,

f — частота в герцах (Гц),

R сопротивление в омах (Ом),

L — индуктивность в генри (Гн),

C — емкость в фарадах (Ф),

Q — добротность последовательной RLC-цепи (безразмерная величина),

ω₀ — резонансная угловая частота в радианах в секунду (рад/с),

f0 — резонансная частота в герцах (Гц),

φ — фазовый сдвиг между полным напряжением V_T и полным током I_T в градусах (°) и радианах и

j — мнимая единица.

Для расчета введите сопротивление, индуктивность, емкость, частоту и выберите единицы измерения. Импеданс RLC –цепи будет показан в омах, сдвиг фаз в градусах и радианах. Также будут рассчитаны добротность, индуктивное и емкостное реактивные сопротивления и резонансная частота. С помощью ссылки Установить резонансную частоту можно рассчитать величины при резонансе.

Последовательная RLC-цепь состоит из резистора R, катушки индуктивности L и конденсатора C, соединенных последовательно. Как и в идеальной последовательной LC-цепи без сопротивления, в RLC-цепи могут возникать колебания с частотой резонанса, которые, однако, затухают из-за наличия сопротивления.

Резонанс возникает на частоте, при которой импеданс цепи минимален, то есть, при нулевом реактивном сопротивлении цепи. Иными словами, он возникает, если импеданс только резистивный, без реактивной составляющей, то есть его мнимая часть равна нулю. Явление резонанса происходит в том случае, когда реактивные сопротивления катушки индуктивности и конденсатора равны и, поскольку они имеют противоположный знак, они гасят друг друга. Как это происходит — показано ниже на векторной диаграмме.

Калькулятор определяет резонансную частоту RLC-цепи, и можно ввести эту частоту или значение чуть-чуть меньше или чуть-чуть больше резонансной частоты, чтобы посмотреть, как будут себя вести рассчитываемые величины при резонансе и около него.

Калькулятор рассчитывает также добротность Q последовательной RLC-цепи — параметр, который используется для характеристики электрических резонансных цепей и устройств, а также механических резонаторов. Чем выше сопротивление цепи, тем больше потерь и тем выше затухание в RLC-цепях и ниже их добротность. Добротность Q последовательной RLC-цепи рассчитывается по приведенной выше формуле.

Слева приведен график зависимости импеданса Z_RLC последовательной RLC-цепи от частоты f при заданных значениях сопротивления, индуктивности и емкости. Видно, что при резонансе импеданс резистивный и реактивная составляющая отсутствует. При повышении частоты реактивное сопротивление катушки индуктивности увеличивается, а конденсатора — уменьшается. Если же частота уменьшается до нуля (то есть источник выдает постоянное напряжение), реактивное сопротивление катушки индуктивности уменьшается до нуля, а конденсатора — становится бесконечно большим. То есть, при нулевой частоте (на постоянном токе) последовательная RLC-цепь представляет собой просто разомкнутую цепь с бесконечно большим импедансом. На правом графике показана зависимость импеданса и разности фаз последовательной RLC-цепи от частоты. Справа от резонанса импеданс имеет индуктивный характер, а слева — емкостной.

На векторной диаграмме последовательной RLC-цепи показан емкостной импеданс (слева), индуктивный импеданс (в центре) и резистивный импеданс при резонансе (справа). Векторы напряжения на графике образуют прямоугольный треугольник с гипотенузой V_T, вертикальным катетом V_L– V_C и горизонтальным катетом V_R. Видно, что при емкостном характере импеданса ток опережает напряжение, а при индуктивном — отстает от него.

В последовательной RLC-цепи один и тот же ток протекает через резистор, конденсатор и катушку индуктивности, однако падения напряжения на элементах этой цепи различны. На векторной диаграмме показано напряжение V_T идеального источника напряжения. В связи с наличием сопротивления, на схеме показан горизонтальный вектор напряжения на резисторе в фазе с текущим через него током. Вектор напряжения на индуктивности V_L отстает от вектора тока на 90°, поэтому он направлен вверх (+90°). Вектор напряжения на емкости опережает вектор тока на 90°, поэтому он направлен вниз (–90°). Векторная сумма двух векторов, направленных в противоположные стороны, может быть направлена вниз и вверх в зависимости от того, на чем больше падение напряжения — на индуктивности или на емкости. Вектор полного напряжения в цепи V_T определяется по теореме Пифагора.

На частоте резонанса емкостное и индуктивное реактивные сопротивления равны и, если посмотреть на приведенное выше уравнение для |Z|, мы увидим, что эффективный импеданс будет определяться только величиной сопротивления и будет минимальным. Через катушку индуктивности и конденсатор, течет одинаковый ток, а падения напряжения на них равны и противоположны по знаку, так как их реактивные сопротивления тоже равны. Поэтому на резонансной частоте от источника потребляется ток, определяемый лишь резистором, так как идеальная последовательная LC-цепь при резонансе представляет собой для источника питания короткое замыкание. При наличии в цепи резистора, последовательная RLC-цепь при резонансе представляет собой чисто резистивную нагрузку.

Резонансная частота последовательной RLC-цепи определяется с учетом, что

Умножая обе стороны уравнения на частоту f, получаем:

Если разделить обе части уравнения на 2πL, извлечь из обеих частей квадратный корень и упростить получившееся выражение, получаем значение резонансной частоты:

Режимы отказа элементов

А что если в этой схеме отказал один из элементов? Нажмите на соответствующую ссылку, чтобы посмотреть соответствующие режимы отказа:

Особые режимы работы цепи

Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:

Различные режимы работы на постоянном токе

Короткое замыкание

Обрыв цепи

Чисто емкостная цепь

Цепь при резонансе

Чисто индуктивная цепь

Индуктивная цепь

Примечания

• Нулевая частота в объяснениях поведения этой цепи означает постоянный ток. Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
• При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
• При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.

Катушки индуктивности в высокочастотном модуле телевизионного приемника

Колебательный контур — Википедия

Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном — параллельным^[1].

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.

Резонансная частота контура определяется так называемой формулой Томсона:

f0=12πLC.{\displaystyle f_{0}={1 \over 2\pi {\sqrt {LC}}}.}

Пусть конденсатор ёмкостью C заряжен до напряжения U0{\displaystyle U_{0}}. Энергия, запасённая в конденсаторе, составляет

EC=CU022.{\displaystyle E_{C}={\frac {CU_{0}^{2}}{2}}.}

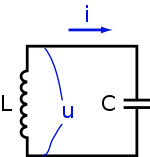Параллельный колебательный контур Осциллограмма LC-контура во время замыкания заряженного конденсатора на катушку индуктивности.
С — 240 нФ (заряженный)
L — 360 нГн
F₀ ≈ 542 кГц

При соединении конденсатора с катушкой индуктивности в цепи потечёт ток I{\displaystyle I}, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности), в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора EC=0{\displaystyle E_{C}=0}. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

EL=LI022,{\displaystyle E_{L}={\frac {LI_{0}^{2}}{2}},}

где L{\displaystyle L} — индуктивность катушки, I0{\displaystyle I_{0}} — максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть зарядка конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор в этом случае снова будет заряжен до напряжения −U0{\displaystyle -U_{0}}.

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

Описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи больше тока, проходящего через весь контур, причём эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.

Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.

Напряжение на идеальной катушке индуктивности при изменении протекающего тока:

uL=LdiLdt.{\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}

Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:

iC=CduCdt.{\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}

Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:

uL+uC=0,{\displaystyle u_{L}+u_{C}=0,} — для напряжений,

и

iC=iL{\displaystyle i_{C}=i_{L}} — для токов.

Совместно решая систему дифференциальных уравнений (дифференцируя одно из уравнений и подставляя результат в другое), получаем:

d2q(t)dt2+1LCq(t)=0.{\displaystyle {\frac {d^{2}q(t)}{dt^{2}}}+{\frac {1}{LC}}q(t)=0.}

Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ω=1LC{\displaystyle \omega ={\frac {1}{\sqrt {LC}}}} (она называется собственной частотой гармонического осциллятора).

Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:

i(t)=Iasin⁡(ωt+φ),{\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi ),}

где Ia{\displaystyle I_{a}} — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, φ{\displaystyle \varphi } — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.

Например, при начальных условиях φ=0{\displaystyle \varphi =0} и амплитуде начального тока Ia{\displaystyle I_{a}} решение сведётся к:

i(t)=Iasin⁡(ωt).{\displaystyle i(t)=I_{a}\sin({\omega }t).}

Решение может быть записано также в виде

i(t)=Ia1sin⁡(ωt)+Ia2cos⁡(ωt),{\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}

где Ia1{\displaystyle I_{a1}} и Ia2{\displaystyle I_{a2}} — некоторые константы, которые связаны с амплитудой Ia{\displaystyle I_{a}} и фазой φ{\displaystyle \varphi } следующими тригонометрическими соотношениями:

Ia1=Iacos⁡(φ),{\displaystyle I_{a1}=I_{a}\cos {(\varphi )},}

Ia2=Iasin⁡(φ).{\displaystyle I_{a2}=I_{a}\sin {(\varphi )}.}

Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как

z^(iω)=iωL1−ω2LC,{\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}

где i — мнимая единица.

Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

ωh=1LC{\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L:

Q=1RLC,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}

где R — активное сопротивление контура. Для параллельного контура:

Q=ReCL,{\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}

где Re=LCRL+C{\displaystyle R_{e}={\frac {L}{CR_{L+C}}}}, (RL+C{\displaystyle R_{L+C}} — сумма активных сопротивлений в цепи катушки и цепи конденсатора^[2]).

Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение^[3] и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении Re{\displaystyle R_{e}}, которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что Re{\displaystyle R_{e}} в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре Re{\displaystyle R_{e}} легко обретает физический смысл — это активное сопротивление провода катушки и проводников цепи.

Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя^[4].

• Попов В. П. Основы теории цепей: Учеб. для вузов / В. П. Попов. — 4-е изд., испр. — М.: Высш. шк., 2003. — 575 с.
• Скрипников Ю. Ф. Колебательный контур — М.: Энергия, 1970—128 с.: ил. — (МРБ; Вып. 739)
• Изюмов Н. М., Линде Д. П. Основы радиотехники. — М.:Радио и связь, 1983

Последовательный колебательный контур | Резонанс напряжений

Обозначение на схеме

Последовательный колебательный контур – это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно. На схемах идеальный последовательный колебательный контур обозначается вот так:

Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:

R  – это суммарное сопротивление потерь катушки и конденсатора

L – собственно сама индуктивность катушки

С – собственно сама емкость конденсатора

Колебательный контур и генератор частоты

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R – это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно “прячется” внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш , а также снимая осциллограмму с самого генератора U_ГЕН.

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

Влияние частоты на сопротивление колебательного контура

Итак,  погнали. В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма – это напряжение с генератора частоты, а желтая осциллограмма – отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600  Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Резонанс

Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:

Это явление носит название резонанса.

Не будем углубляться  в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.

Как вы помните, если у нас сопротивление  становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома:

I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.

Формула Томсона

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор – это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию  или с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как  среднеквадратичное напряжение  будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите – полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока – увы! Поэтому последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Давайте  обобщим, что у нас получилось в этих опытах.

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Добротность

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R – сопротивление потерь в контуре, Ом

L – индуктивность, Генри

С – емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура – это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса – индуктивную составляющую тока.

Программа для расчета элементов колебательного контура

Программа «Induktiw1» (328 кб) для расчета элементов колебательного контура.
Написать данную программу, как всегда подталкивают определенные обстоятельства. Программа написана для того чтобы автоматизировать процесс расчета элементов колебательного контура. Данная программа универсальна и позволяет выполнять расчеты величины индуктивности контура для заданной вами частоты — рис.1.

Рис.1. Расчёт колебательного контура (например 100МГц)

Производить вычисления при расчете однослойной катушки со сплошной обмоткой в зависимости от диаметра и длины намотки — рис.2

Рис.2. Расчет однослойной катушки со сплошной обмоткой

Проводить вычисления для катушек разной конструкции, в том числе и для бифильярной намотки многослойных катушек индуктивности — рис.3.

Рис.3. Расчёт для многослоной катушки (между щечками)

В связи с распространением различных трансформаторов и дросселей на кольцевых магнитопроводах можно производить расчет тороидальной катушки на кольце — рис.4.

Рис.4. Расчет тороидально катушки (на кольце)

По имеющимся у вас параметрам катушки намотанной на кольцевом магнитопроводе можно рассчитать индуктивность тороидальной катушки — рис.5.

Рис.5. Индуктивность тороидальной катушки

Для расчета элементов настройки колебательного контура можно проводить расчеты конденсаторов настройки данного контура от имеющихся уже у вас в наличии или тех, что нужно вам установить — рис.6.

Рис.6. Расчет конденсатора настройки

 

Г. Тяпичев, RA3XB

Калькулятор импеданса последовательной LC-цепи, Электротехнические и радиотехнические калькуляторы, Конвертер величин

Калькулятор определяет импеданс и фазовый сдвиг для соединенных последовательно идеальной катушки индуктивности и идеального конденсатора для заданной частоты синусоидального сигнала. Определяется также угловая частота.

Пример. Рассчитать импеданс катушки индуктивности 100 мГн и конденсатора 800 нФ на частоте 562 Гц. Калькулятор показывает импеданс около 0,9 Ом. Это почти резонанс. Можно проверить импеданс при почти полном резонансе, если ввести 562,6977 Гц вместо 562 Гц. При этой частоте импеданс получается индуктивным. Однако, если ввести чуть большую частоту 562,69767 Гц, импеданс станет емкостным, и вы увидите, что фазовый угол, который был чуть меньше нуля, стал положительным.

Входные данные

Индуктивность, L

генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)

Емкость, С

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Частота, f

герц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц)

Выходные данные

Угловая частота ω= рад/с

Емкостное реактивное сопротивление X_C= Ом

Емкостное реактивное сопротивление X_L= Ом

Полный импеданс LC |Z_LC|= Ом

Фазовый сдвигφ = ° = рад

Резонансная частота

f₀=   Гц   ω₀=   рад/с

Введите значения емкости, индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Попробуйте ввести нулевые или бесконечно большие значения величин, чтобы посмотреть как будет себя вести эта цепь. Бесконечная частота не поддерживается. Для ввода значения бесконечность наберите inf.

Для расчетов используются указанные ниже формулы:

φ = 90° если 1/(2πfC) < 2πfL

φ = –90° если 1/(2πfC) > 2πfL

φ = 0° если 1/(2πfC) = 2πfL

Здесь

Z_LC — импеданс цепи LC в омах (Ом),

ω = 2πf — угловая частота в рад/с,

f — частота в герцах (Гц),

L — индуктивность в генри (Гн),

C — емкость в фарадах (Ф),

ω₀ — резонансная угловая частота в радианах в секунду (рад/с),

f₀ — резонансная частота в герцах (Гц),

X_C — реактивное сопротивление конденсатора в омах (Ом),

X_L — реактивное сопротивление катушки индуктивности в омах (Ом),

φ — фазовый сдвиг между полным напряжением V_T и полным током I_T в градусах (°) и радианах,

j — мнимая единица.

Для расчета введите сопротивление, индуктивность, емкость, частоту и выберите единицы измерения. Импеданс RLC –цепи будет показан в омах, сдвиг фаз в градусах и радианах. Также будут рассчитаны индуктивное и емкостное реактивные сопротивления и резонансная частота. С помощью ссылки Вычислить на резонансной частоте можно рассчитать величины при резонансе.

Последовательная LC-цепь состоит из катушки индуктивности L и конденсатора C, соединенных последовательно. В LC-цепи могут возникать колебания с частотой резонанса. Резонанс возникает на частоте, при которой импеданс цепи минимален, то есть, при нулевом реактивном сопротивлении цепи. Явление резонанса происходит в том случае, когда реактивные сопротивления катушки индуктивности и конденсатора равны и, поскольку они имеют противоположный знак, они гасят друг друга. Как это происходит — показано ниже на векторной диаграмме.

Графики зависимости импеданса Z_LC последовательной LC-цепи от частоты f при заданных значениях сопротивления, индуктивности и емкости. Видно, что при резонансе импеданс резистивный и реактивная составляющая отсутствует. При повышении частоты реактивное сопротивление катушки индуктивности увеличивается, а конденсатора — уменьшается. Если же частота уменьшается до нуля (то есть источник выдает постоянное напряжение), реактивное сопротивление катушки индуктивности уменьшается до нуля, а конденсатора — становится бесконечно большим. То есть, при нулевой частоте (на постоянном токе) последовательная LC-цепь представляет собой просто разомкнутую цепь с бесконечно большим импедансом. Отметим, что справа от резонанса импеданс имеет индуктивный характер, а слева — емкостной.

Калькулятор определяет резонансную частоту LC-цепи, и можно ввести эту частоту или значение чуть-чуть меньше или чуть-чуть больше резонансной частоты, чтобы посмотреть, как будут себя вести рассчитываемые величины при резонансе и около него.

На векторной диаграмме последовательной LC-цепи слева показан емкостной импеданс, при котором цепь представляет собой емкостную нагрузку; на центральной диаграмме показан индуктивный импеданс, при котором цепь представляет собой индуктивную нагрузку; резонанс с нулевым импедансом показан на правой диаграмме

В последовательной LC-цепи один и тот же ток протекает через конденсатор и катушку индуктивности, однако падения напряжения на элементах этой цепи различны. На векторной диаграмме показано напряжение V_T идеального источника напряжения. Поскольку активное сопротивление в этой цепи равно нулю, на схеме не показан горизонтальный вектор напряжения в фазе с текущим через цепь током. Вектор напряжения на индуктивности V_L отстает от вектора тока на 90°, поэтому он направлен вверх (+90°). Вектор напряжения на емкости опережает вектор тока на 90°, поэтому он направлен вниз (–90°). Векторная сумма двух векторов, направленных в противоположные стороны, может быть направлена вниз и вверх в зависимости от того, на чем больше падение напряжения — на индуктивности или на емкости.

На частоте резонанса емкостное и индуктивное реактивные сопротивления равны и, если посмотреть на приведенное выше уравнение для |Z|, мы увидим, что эффективный импеданс равен нулю, так как два вектора напряжения, направленные в противоположные стороны, гасят друг друга. Через катушку индуктивности и конденсатор течет одинаковый ток, а падения напряжения на них равны и противоположны по знаку, так как их реактивные сопротивления тоже равны. Поэтому на резонансной частоте от источника потребляется теоретически бесконечный ток, так как идеальная последовательная LC-цепь при резонансе представляет собой для источника питания короткое замыкание. В реальной жизни катушки индуктивности всегда имеют небольшое сопротивление, которое ограничивает ток. Реальные источники напряжения также не могут отдавать в нагрузку бесконечно большой ток, так как он ограничен внутренним сопротивлением источника питания.

Резонансная частота последовательной RLC-цепи определяется с учетом, что

Умножая обе стороны уравнения на частоту f, получаем:

Если разделить обе части уравнения на 2πL, извлечь из обеих частей квадратный корень и упростить получившееся выражение, получаем значение резонансной частоты:

Катушки индуктивности в высокочастотном модуле телевизионного приемника

Режимы отказа элементов

А что если в этой схеме отказал один из элементов? Нажмите на соответствующую ссылку, чтобы посмотреть соответствующие режимы отказа:

Особые режимы работы цепи

Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:

Различные режимы работы на постоянном токе

Короткое замыкание

Обрыв цепи

Чисто емкостная цепь

Цепь при резонансе

Чисто индуктивная цепь

Индуктивная цепь

Примечания

• Нулевая частота в объяснениях поведения этой цепи означает постоянный ток. Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
• При нулевой частоте реактивное сопротивление конденсатора считается нулевым, если его емкость бесконечно большая. Если же емкость конденсатора конечная или нулевая, его реактивное сопротивление бесконечно большое и для источника постоянного напряжения он представляет собой обрыв цепи, иными словами отсутствующий конденсатор.
• При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.

Колебательный контур. LCR, LC — контур. Катушка индуктивности, конденсатор Формула Томсона Энергия

Колебательный контур – электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью

, катушки с индуктивностью и электрического сопротивления .

Идеальный колебательный контур — цепь, состоящая только из катушки индуктивности (не имеющей собственного сопротивления) и конденсатора (

-контур). Тогда в такой системе поддерживаются незатухающие электромагнитные колебания силы тока в цепи, напряжения на конденсаторе и заряда конденсатора. Давайте разберём контур и подумаем, откуда возникают колебания. Пусть изначально заряженный конденсатор помещён в описываемую нами цепь.

Рис. 1. Колебательный контур

В начальный момент времени весь заряд сосредоточен на конденсаторе, на катушке тока нет (рис. 1.1). Т.к. на обкладках конденсатора внешнего поля тоже нет, то электроны с обкладок начинают «уходить» в цепь (заряд на конденсаторе начинает уменьшаться). При этом (за счёт освобождённых электронов) возрастает ток в цепи. Направление тока, в данном случае, от плюса к минусу (впрочем, как и всегда), и конденсатор представляет собой источник переменного тока для данной системы. Однако при росте тока на катушке, вследствие явления электромагнитной индукции, возникает обратный индукционный ток (

). Направление индукционного тока, согласно правилу Ленца, должно нивелировать (уменьшать) рост основного тока. Когда заряд конденсатора станет равным нулю (весь заряд стечёт), сила индукционного тока в катушке станет максимальной (рис. 1.2).

Однако текущий заряд в цепи пропасть не может (закон сохранения заряда), тогда этот заряд, ушедший с одной обкладки через цепь, оказался на другой обкладке. Таким образом, происходит перезарядка конденсатора в обратную сторону (рис. 1.3). Индукционный ток на катушке уменьшается до нуля, т.к. изменение магнитного потока также стремится к нулю.

При полной зарядке конденсатора электроны начинают двигаться в обратную сторону, т.е. происходит разрядка конденсатора в обратную сторону и возникает ток, доходящий до своего максимума при полной разрядке конденсатора (рис. 1.4).

Дальнейшая обратная зарядка конденсатора приводит в систему в положение на рисунке 1.1. Такое поведение системы повторяется сколь угодно долго. Таким образом, мы получаем колебание различных параметров системы: тока в катушке, заряд на конденсаторе, напряжение на конденсаторе. В случае идеальности контура и проводов (отсутствие собственного сопротивления), эти колебания — гармонические.

Для математического описания этих параметров этой системы (в первую очередь, периода электромагнитных колебаний) вводится рассчитанная до нас формула Томсона:

(1)

Неидеальным контуром является всё тот же идеальный контур, который мы рассмотрели, с одним небольшим включением: с наличием сопротивления

(-контур). Данное сопротивление может быть как сопротивлением катушки (она не идеальна), так и сопротивлением проводящих проводов. Общая логика возникновения колебаний в неидеальном контуре аналогична той, что и в идеальном. Отличие только в самих колебаниях. В случае наличия сопротивления, часть энергии будет рассеиваться в окружающую среду — сопротивление будет нагреваться, тогда энергия колебательного контура будет уменьшаться и сами колебания станут затухающими.

Для работы с контурами в школе используется только общая энергетическая логика. В данном случае, считаем, что полная энергия системы в начале сосредоточена на конденсаторе и/или катушке, и описывается:

 

(2)

(3)

Для идеального контура полная энергия системы остаётся постоянной:

(4)

• где
  • — полная энергия колебательной системы.

Для неидеального контура часть начальной энергии переходит в тепло, что можно описать законом Джоуля-Ленца. Тогда энергетические превращения в таком контуре можно описать:

(5)

Вывод: работа с контурами достаточно сложна. Чаще всего это работа со схемами, в которых присутствуют ключи. Энергетически рассмотреть переход из начального состояния в конечное практически невозможно, тогда стоит работать с начальным и конечным положением системы. Определяем вид контура (идеальный/неидеальный) и рассмотреть энергию системы в обоих случаях. Далее, используя (4) или (5), получаем уравнение, которое можно решать.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…