Онлайн калькулятор — расчет сопротивления заземления

Грамотный расчет сопротивления заземления позволяет с высокой точностью определить основной показатель устройства, характеризующий величину стекающего тока и эффективность действия защитного приспособления. Значение этого параметра, в конечном счете, определяется габаритами рабочего контура, а также его составом и формой применяемых в конструкции элементов.

Из чего состоит устройство заземления

В общем случае устройство заземления представляет собой несложное сооружение, состоящее из следующих основных частей:

1. вертикально вбиваемых в землю металлических прутков диаметром не менее12-ти мм;
2. горизонтальных перемычек в виде пластин, объединяющих вбитые в землю прутья;
3. комплекта медных проводников, посредством которых контур соединяется с главной заземляющей шиной (ГЗШ), смонтированной в распределительном щитке в пределах объекта.

Важно! Поскольку рабочая цепочка элементов заземления имеет несколько контактных точек – их учет очень важен при расчете общей величины переходного сопротивления.

Расчет с помощью калькулятора

Чтобы рассчитать все эти показатели – удобнее всего воспользоваться онлайн-калькулятором, предназначенным для определения точных значений для двухслойного грунта. При вводе данных учитываются следующие рабочие параметры:

• Климатический коэффициент для верхнего слоя грунта.
• Количество вертикально вбитых прутьев (штуки).
• Толщина верхнего грунтового слоя, H (метры).
• Длина вертикальных заземлителей, L1 (метры).
• Глубина размещения горизонтальных заземлителей (соединительной полосы), h3 (метры).
• Длина соединительной полосы, L3 (метры).
• Диаметр прутьев, D (метры).
• Также учитывается ширина полки горизонтально монтируемой части, b (метры).

Внимание! Для разделения целой и дробной части числа ставьте точку.

Расчет с помощью формул

Со всеми этими параметрами можно ознакомиться на приведенном выше рисунке. Из него видно, что после ввода указанных выше данных удается получить результирующие значения. В общем случае они представлены сопротивлением для двух видов контуров: с одиночным и групповым заземлителем.

В результатах вычислений вы увидите следующие готовые значения:

1. Удельного сопротивления грунта
2. Сопротивление вертикального и горизонтального заземлителя
3. Общее сопротивление растеканию электрического тока.

Какое должно быть сопротивление растеканию тока заземляющего устройства?

Читаем правила ПУЭ п. 1.7.102:

Общее сопротивление растеканию заземлителей (в том числе естественных) всех повторных заземлений PEN-проводника каждой ВЛ в любое время года должно быть не более 5, 10 и 20 Ом соответственно при линейных напряжениях 660, 380 и 220 В источника трехфазного тока или 380, 220 и 127 В источника однофазного тока. При этом сопротивление растеканию заземлителя каждого из повторных заземлений должно быть не более 15, 30 и 60 Ом соответственно при тех же напряжениях.

После применения онлайн-калькулятора для расчета сопротивления заземления предлагаем Вам ознакомиться со следующими статьями:

Расчет сопротивления онлайн по схеме — Moy-Instrument.Ru

Конвертер величин

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются

для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Расчет сопротивления онлайн по схеме

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

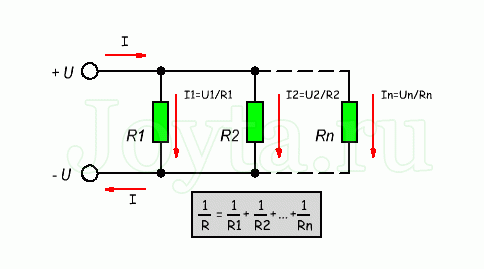
Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

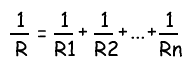
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

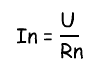
Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

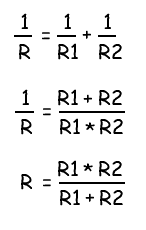
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

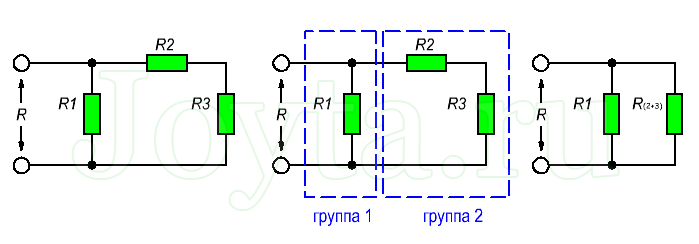
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

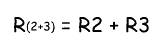
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений

Разделы: Физика

Цели:

Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
• Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.
• Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.

Тип урока: урок проверки и закрепления новых знаний по физике и математике.

Метод проведения урока: практический

Оборудование:

• Громов С.В. Учебник “Физики-9”;
• план урока;
• методика расчета участка электрической цепи постоянного тока;
• карточки-задания.

Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.

Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:

1) Какие виды соединений бывают и как они изображаются на электрических схемах?
2) Назовите законы последовательного соединения?
3) Назовите законы параллельного соединения?
4) Какая отличительная особенность параллельного соединения?

Рассмотрим расчёт участка электрической цепи на примере следующих задач:

1. Рассчитайте общее электрическое сопротивление участка цепи?

1) Наиболее удалённые от источника элементы – это резисторы R₂ и R₃.

2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R₂ и R₃ подключены параллельно, т.к образуют в соединении два узла, следовательно:

Ом

3) Изображаем получившуюся в результате свёртывания резисторы R₂ и R₃ электрическую схему:

4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R₁ и R_об.1 соединены последовательно, значит:

Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.

2. Рассчитайте общее электрическое сопротивление участка цепи?

1) Резисторы R₁ и R₂ соединены между собой последовательно:

Изобразим полученный электрический участок цепи:

2) Резисторы R₃ и R₄ соединены между собой последовательно:

Изобразим полученный электрический участок цепи:

3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы R_об.1 и R_об.2 соединены параллельно, значит:

Ом

Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.

3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:

а) Рассчитайте общее электрическое сопротивление участка цепи?

б) Рассчитайте общее электрическое сопротивление участка цепи?

в) Рассчитайте общее электрическое сопротивление участка цепи?

Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.

Онлайн калькулятор для параллельного соединения резисторов

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Видео: Последовательное и параллельное соединение проводников

Параллельное соединение: общая информация

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

• R(общ) – суммарное значение сопротивления;
• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчёта

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Видео: Правильное подключение светодиодов

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Правильный расчет резистора для светодиода, подбор резистора по цветовой маркировке + онлайн калькулятор

Светоизлучающие диоды, характеризуются рядом эксплуатационных параметров:

• Номинальный (рабочий) ток – I_н;
• падение напряжения при номинальном токе – U_н;
• максимальная рассеиваемая мощность – P_max;
• максимально допустимое обратное напряжение – U_обр.

Самым важным из перечисленных параметров является рабочий ток.

При протекании через светодиод номинального рабочего тока – номинальный световой поток, рабочее напряжение и номинальная рассеиваемая мощность устанавливаются автоматически. Для того чтобы задать рабочий режим LED, достаточно задать номинальный ток светодиода.

В теории светодиоды нужно подключать к источникам постоянного тока. Однако, на практике, LED подключают к источникам постоянного напряжения: батарейки, трансформаторы с выпрямителями или электронные преобразователи напряжения (драйверы).

Для задания рабочего режима светодиода, применяют простейшее решение – последовательно с LED включают токоограничивающий резистор. Их еще называют гасящими или балластными сопротивлениями.

Рассмотрим, как выполняется расчет сопротивления резистора для светодиода.

Расчет резистора светодиода (по формулам)

При расчете вычисляют две величины:

• Сопротивление (номинал) резистора;
• рассеиваемую им мощность P.

Источники напряжения, питающие LED, имеют разное выходное напряжение. Для того чтобы выполнить подбор резистора для светодиода нужно знать напряжение источника (U_ист), рабочее падение напряжения на диоде и его номинальный ток. Формула для расчета выглядит следующим образом:

При вычитании из напряжения источника номинальное падение напряжения на светодиоде – мы получаем падение напряжения на резисторе. Разделив получившееся значение на ток мы, по закону Ома, получаем номинал токоограничивающего резистора. Подставляем напряжение, выраженное в вольтах, ток – в амперах и получаем номинал, выраженный в омах.

Электрическую мощность, рассеиваемую на гасящем сопротивлении, вычисляют по следующей формуле:

P = (I_н) 2 ⋅ R

Исходя из полученного значения, выбирается мощность балластного резистора. Для надежной работы устройства она должна быть выше расчетного значения. Разберем пример расчета.

Пример расчета резистора для светодиода 12 В

Рассчитаем сопротивление для LED, питающегося от источника постоянного напряжения 12В.

Допустим в нашем распоряжении имеется популярный сверхяркий SMD 2835 (2.8мм x 3.5мм) с рабочим током 150мА и падением напряжения 3,2В. SMD 2835 имеет электрическую мощность 0,5 ватта. Подставим исходные значения в формулу.

R = (12 — 3,2) / 0,15 ≈ 60

Получаем, что подойдет гасящий резистор сопротивлением 60 Ом. Ближайшее значение из стандартного ряда Е24 – 62 ома. Таким образом, для выбранного нами светодиода можно применить балласт сопротивлением 62Ом.

Теперь вычислим рассеиваемую мощность на сопротивлении.

P = (0,15) 2 ⋅ 62 ≈ 1,4

На выбранном нами сопротивлении будет рассеиваться почти полтора ватта электрической мощности. Значит, для наших целей можно применить резистор с максимально допустимой рассеиваемой мощностью 2Вт.

Осталось купить резистор с подходящим номиналом. Если же у вас есть старые платы, с которх можно выпаять детали, то по цветовой маркировке можно выполнить подбор резистора. Воспользуйтесь формой ниже.

На заметку! В приведенном выше примере на токоограничительном сопротивлении рассеивается почти в три раза больше энергии, чем на светодиоде. Это означает, что с учетом световой отдачи LED, КПД нашей конструкции меньше 25%.

Чтобы снизить потери энергии лучше применить источник с более низким напряжением. Например, для питания можно применить преобразователь постоянного напряжения AC/AC 12/5 вольт. Даже с учетом КПД преобразователя потери будут значительно меньше.

Параллельное соединение

Довольно часто требуется подключить несколько диодов к одному источнику. Теоретически, для питания нескольких параллельно соединенных LED, можно применить один токоограничивающий резистор. При этом формулы будут иметь следующий вид:

P = (n ⋅ I_н) 2 ⋅ R

Где n – количество параллельно включенных ЛЕДов.

Почему нельзя использовать один резистор для нескольких параллельных диодов

Даже в «китайских» изделиях производители для каждого светодиода устанавливают отдельный токоограничивающий резистор. Дело в том, что в случае общего балласта для нескольких LED многократно возрастает вероятность выхода из строя светоизлучающих диодов.

В случае обрыва одного из полупроводников, его ток перераспределится через оставшиеся LED. Рассеиваемая на них мощность увеличится и они начнут интенсивно нагреваться. Вследствие перегрева следующий диод выйдет из строя и дальше процесс примет лавинообразный характер.

Совет. Если по какой-то причине нужно обойтись одним гасящим сопротивлением, увеличьте его номинал на 20-25%. Это обеспечит большую надежность конструкции.

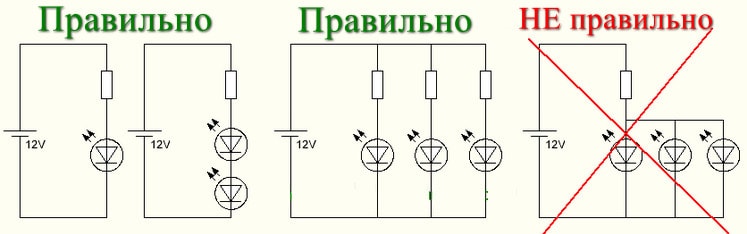Пример правильного подключения резистора

Можно ли обойтись без резисторов?

Действительно, в некоторых случаях можно не использовать токоограничивающий резистор. Рассмотренный нами светодиод можно напрямую запитать от двух батареек 1,5В. Так как его рабочее напряжение составляет 3,2В, то протекающий через него ток будет меньше номинального и балласт ему не потребуется. Конечно, при таком питании светодиод не будет выдавать полный световой поток.

Иногда в цепях переменного тока в качестве токоограничивающих элементов вместо резисторов применяют конденсаторы (подробнее про расчет конденсатора). В качестве примера можно привести выключатели с подсветкой, в которых конденсаторы являются «безваттными» сопротивлениями.

Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн



 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Расчёт реактивного сопротивления конденсатора и индуктивности. Он-лайн калькулятор сопротивлений ёмкости Xc и индуктивности Xl переменному току.

Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и задуматься — а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича после преобразования частотно-зависимыми цепями, и что это за цепи такие — частотно-зависимые?

Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и резистивных элементов. Спасибо, господа нефтяники и газовики — будем знать. От себя добавлю, что индуктивные элементы в частотно-зависимом хозяйстве также иногда пригождаются.

Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора — бесконечность, индуктивности — ноль. Другое дело — переменный ток, тут наши частотно-зависимые элементы, начинают приобретать определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от частоты протекающего тока. Для особо продвинутых, вымучаю из себя умную фразу — «Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах».

Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав, пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому сразу перейдём к делу и напишем всего пару формул:

Xс = 1 / 2πƒС,   Xl = 2πƒL, где
Xc — сопротивление конденсатора переменному току, а Xl — сопротивление индуктивности переменному току.

РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА

ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ

В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и индуктивностью, а катушки индуктивности — омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.

Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения — знать надо обязательно.
Делают они это, ни кем не посоветовавшись, эффектно, громко, с выделение токсичных паров электролита в виде облака из дыма, и с лёкгостью могут выбить глаз пытливому радиолюбителю.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты приличных производителей.