Расчёт частоты резонанса колебательного контура
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью
 .
. Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке,
что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора
индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1,
он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени
В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости
XC=1/(2πfC).Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Частота резонанса колебательного контура LC. |
Расчёт ёмкости:
Ёмкость для колебательного контура LC |
Расчёт индуктивности:
Индуктивность для колебательного контура LC |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Калькулятор резонанса колебательного контура — MOREREMONTA
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Свободные электрические колебания в параллельном контуре.
Основные свойства индуктивности:
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией  .
.
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Период свободных колебаний контура LC можно описать следующим образом:
Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
.
Если параллельно заряженному конденсатору подключить катушку индуктивности

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 =  .
.
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, EC будет равна EL. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.
В течении заключительного этапа колебания (
t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний  .
.
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL равно реактивному сопротивлению ёмкости XC=1/(2πfC).
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчёт ёмкости:
Расчёт индуктивности:
Похожие страницы с расчётами:
Замечания и предложения принимаются и приветствуются!
Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно. — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты внешнего воздействия с некоторыми значениями (резонансными частотами), определяемыми свойствами системы.
F=1/(2π×√L×C), где
F — Резонансная частота, Гц)
L — Индуктивность, (Гн)
C — Ёмкость, (Ф)
Сайт для радиолюбителей
 Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным.
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Резонансная частота контура определяется так называемой формулой Томсона:
При слишком малой индуктивности и большой емкости будет падать резонансное сопротивление контура, что приведет к ухудшению его избирательных свойств, а в схеме резонансного усилителя упадет усиление каскада. При слишком малой емкости и большой индуктивности катушка будет содержать большое количество витков, добротность ее будет уменьшаться, а собственная емкость расти, в результате она может сравняться с емкостью контурного конденсатора, что не допустимо. Также на настройку контура будет влиять емкость монтажа, ведь она соизмерима со значением С. Исходя из вышеуказанного, рекомендую выбирать соотношение емкости к индуктивности примерно как 100000 : 1 в абсолютном значении, что подходит для большинства контуров.
Например, для частоты 10,7 МГц оптимальным будет С=47 пФ и L= 4,7 мкГн, а для частоты 465 кГц оптимальные С=1000пФ и L=117мкГн.
Исходя из всего выше сказанного, онлайн калькулятор позволяет подобрать значения емкости и индуктивности в пределах ±20% от оптимального значения.
Для расчета частоты резонанса колебательного контура LC заполните предложенную форму:
Расчёт ёмкости для колебательного контура LC
Расчёт индуктивности для колебательного контура LC
Расчёт LC — фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.
LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, который на Сотбисе не купишь!
Как ни крути, а не получил бы Александр Степаныч наш Попов звание почётного инженера-электрика, не направь он искровой разряд
напрямик в колебательный контур для обретения благословения свыше и резонанса с передающей антенной.
И заскучала бы братва копателей свободной энергии эфира, не изобрети Никола Тесла свой резонансный трансформатор и
электрический автомобиль с неведомой коробочкой. А то и вовсе, заширялась бы в подъездах, лишённая идей вселенского масштаба.
И начнём мы с расчёта самого простого LC-фильтра — колебательного контура.
Включённый по приведённой на рис.1 схеме, он представляет собой узкополосный полосовой фильтр, настроенный на частоту
fо= 1/2π√LС.
На резонансной частоте сопротивление контура равно:
Rо = pQ, где р — характеристическое сопротивление, равное реактивному сопротивлению катушки и конденсатора.
Оно в свою очередь рассчитывается по формуле р = √L/C.
Рис.1
На низких (звуковых) частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки
индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше
провод, тем проще его измерить тестером. Если эта попытка удалась, то Q=2πfL/R, где R – активное сопротивление катушки индуктивности.
На радиочастотах значение активного сопротивления катушки может составлять доли ома, поэтому для расчёта добротности надо — либо
найти сопротивление в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в
метрах, d — диаметр провода в мм, либо вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким
внутренним сопротивлением, и определить добротность экспериментально.
К тому же на высоких частотах возможно проявление влияния добротности конденсатора, особенно если он окажется варикапом, хотя
современные недорогие керамические изделия (например, фирмы Murata) имеют значение параметра добротности — не менее 800.
Нарисуем табличку с расчётом фильтра для низкочастотных приложений.
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.
Если параметр активного сопротивления катушки R опущен, его значение принимается равным 200 омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура.
При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую
конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике
десятки кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядок меньше
характеристического сопротивления ρ.
Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана,
эффект близости витков и т. д.
Поэтому вводить этот параметр в качестве входного я не
стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом
значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей
частоты (Q=2πfL/R).
К тому же я добавлю сюда
параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора — 1000, а для
испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу
ссылка на страницу .
ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.
Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).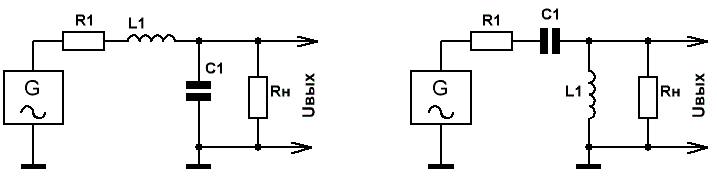
Рис.2
Крутизна спада АЧХ этих фильтров в полосе подавления — 12 дБ/октаву, коэффициент передачи в полосе пропускания К=1 при R1
Однако наилучшие параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются
при R1=Rн=ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.
Ну да ладно, ближе к делу.
ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
А если надо рассчитать L и C при известных значениях Fср и ρ ? Не вопрос,
ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.
Данные ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно,
чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу).
При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.
Рис.3
ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы — катушками.
Широкополосные полосовые LC — фильтры получают каскадным соединением ФНЧ и ФВЧ.
Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.


Расчет колебательного контура
Практический расчет последовательного или параллельного LC контура.
Доброго дня уважаемые радиолюбители!
Сегодня мы с вами рассмотрим порядок расчета LC контура.
Некоторые из вас могут спросить, а на черта нам это нужно? Ну, во-первых, лишние знания никогда не помешают, а во-вторых, бывают в жизни моменты, когда вам знание этих расчетов может понадобиться. К примеру, очень многие начинающие радиолюбители (естественно, в основном молодые), увлекаются сборкой так называемых “жучков” – устройств позволяющих на расстоянии прослушивать что-нибудь. Конечно я уверен, что это делается без всяких нехороших (даже грязных) мыслей подслушать кого-нибудь, а в благих целях. Например устанавливают “жучок” в комнате с малышом, а на радиовещательный приемник прослушивают не проснулся ли он. Все схемы “радиожучков” работают на определенной частоте, но что делать, когда эта частота вас не устраивает. Вот тут вам придет на помощь знание нижеприведенной статьи.
LC колебательные контура применяются практически в любой аппаратуре, работающей на радиочастотах. Как известно из курса физики, колебательный контур состоит из катушки индуктивности и конденсатора (емкости), которые могут быть включены параллельно (параллельный контур) или последовательно (последовательный контур), как на рис.1:
Реактивные сопротивления индуктивности и емкости, как известно, зависят от частоты переменного тока. При увеличении частоты реактивное сопротивление индуктивности растет, а емкости – падает. При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное – растет. Таким образом, для каждого контура есть некоторая частота резонанса, на которой индуктивное и емкостное сопротивления оказываются равными. В момент резонанса резко увеличивается амплитуда переменного напряжения на параллельном контуре или резко увеличивается амплитуда тока на последовательном контуре. На рис.2 показан график зависимости напряжения на параллельном контуре или тока на последовательном контуре от частоты:
На частоте резонанса эти величины имеют максимальное значение. А полоса пропускания контура определяется на уровне 0,7 от максимальной амплитуды, которая есть на частоте резонанса.
Теперь перейдем к практике. Предположим нам нужно сделать параллельный контур, имеющий резонанс на частоте 1 МГц. Прежде всего нужно сделать предварительный расчет такого контура. То есть, определить необходимую емкость конденсатора и индуктивность катушки. Для предварительного расчета есть упрощенная формула:
L=(159,1/F)2/C где:
L – индуктивность катушки в мкГн;
С – емкость конденсатора в пФ;
F – частота в МГц
Зададимся частотой 1 МГц и емкостью, к примеру, 1000 пФ. Получим:
L=(159,1/1)2 /1000 = 25 мкГн
Таким образом, если мы захотим контур на частоту 1 МГц, то нужен конденсатор на 1000 пФ и индуктивность на 25 мкГн. Конденсатор можно подобрать,, а вот индуктивность нужно сделать самостоятельно.
Рассчитать число витков для катушки без сердечника можно по такой формуле:
N=32 *√(L/D) где:
N – требуемое число витков;
L – заданная индуктивность в мкГн;
D – диаметр каркаса в мм, на котором предполагается намотать катушку.
Предположим, диаметр каркаса – 5 мм, тогда:
N=32*√(25/5) = 72 витка.
Данная формула является приближенной, она не учитывает собственную межвитковую емкость катушки. Формула служит для предварительного вычисления параметров катушки, которые затем настраиваются при настройке контура.
В радиолюбительской практике чаще используются катушки с подстроечными сердечниками из феррита, имеющими длину 12-14 мм и диаметр 2,5 – 3 мм. Такие сердечники, например, применяются в контурах телевизоров и приемников. Для предварительного расчета числа витков для такого сердечника есть другая приближенная формула:
N=8,5*√L , подставляем значения для нашего контура N=8,5*√25 = 43 витка. То есть, в таком случае на потребуется намотать на катушку 43 витка провода.
Совмещение LC-резонанса и режима стоячих волн в катушке индуктивности. Расчет онлайн
Для того, чтобы поделиться созданным вами проектом, нужно скопировать ссылку и вставить её в блог, форум или другой сайт:
Известно, что катушка обладает собственной индуктивностью и ёмкостью, а значит, и собственным LC-резонансом. Если же катушку рассматривать, как длинную линию, то при определённых частотах в ней будет возникать также и режим стоячих волн. Совмещение этих двух режимов приводит к резкому увеличичению добротности контура и КПД второго рода (η2) в реальных устройствах. Подробнее об этом читайте здесь.
В данном моделировании задейстованы достаточно точные формулы для определения индуктивности и собственной ёмкости катушки, а также данные, учитывающие нелинейный характер изменения скорости распостранения волны в зависимости от частоты и параметров намотки.
На графике, по горизонтальной оси откладываются значения коэффициента намотки, который находится, как отношение шага намотки к диаметру жилы провода. По сути, этот коэффициент определяет конструкцию катушки. По вертикальной оси отложены значения частот в мегагерцах. Оранжевая кривая отражает LC-резонанс, а синий — волновой. Справа от графика приводятся данные самой катушки, которые просчитаны для точки пересечения этих кривых.
Для расширения вычислительного диапазона добавлена возможность подключения к катушке внешней дополнительной ёмкости, а для особых режимов — работа на любой гармонике LC-резонанса (по умолчанию — на первой).
Дополнительно можно ввести данные относительной диэлектрической проницаемости каркаса катушки и его толщины. По умолчанию, относительная диэлектрическая проницаемость равна единице.
Сохранение данных
Этот калькулятор может сохранять полученные вычисления в ваш аккаунт. Для этого вы должны быть зарегистрированы на этом сайте. Вы можете сохранить результат вычисления, который здесь называется словом «проект», нажав на кнопку «Сохранить в аккаунт», а затем полностью восстановить данные из раздела «Мои проекты». Используемые материалыОшибка соединения с сервером. Попробуйте отправить запрос позже!
Данные, принятые от сервера, имеют неправильный формат. Обратитесь к администратору!
Пожалуйста, авторизуйтесь!
Пожалуйста, продлите абонемент!
Процесс вычисления вышел за допустимые процессором рамки: 10 в степени 200. Пожалуйста, измените параметры!
Пожалуйста, авторизуйтесь!
Пожалуйста, продлите абонемент!
Введите название или номер своего проекта
Проект не сохранён!
Данные успешно сохранены
Проект с такими параметрами уже был сохранён в течение последнего часа. Выберите другие параметры!
Вычисления онлайн
Вычисления онлайнВычисления онлайн
- Лабораторная работа по получению некоторых важных параметров и графиков зависимости магнитной проницаемости ферромагнетиков от напряженности магнитного поля. В результате её проведения пользователь получает все необходимые данные для построения реальных генераторов и экспериментов с катушками индуктивности. В дополнение к вузовской лабораторной работе, калькулятор подсчитывает теоретически достижимое значение приращения КПД второго рода при параметрическом изменении индуктивности с обратной ЭДС. Теоретическое обоснование получения дополнительной энергии из обратной ЭДС в катушке индуктивности с сердечником приводится здесь.
- Калькулятор предназначен для расчёта параметров однослойной катушки на 1/4 длины волны, с учётом ёмкости заземления. Подключение внешних ёмкостей: тора и конденсатора, делает возможным и классический расчёт трансформатора Тесла. Нижний подраздел этого калькулятора посвящён точному определению значения ёмкости заземления для данной катушки в вашей местности.
- Новая версия онлайн калькулятора для совмещения различных типов волн в однослойной катушке индуктивности. Производится подсчёт всевозможных параметров катушки в зависимости от её конструктива и материала каркаса. Учитывается её заземление и экранирование. Предыдущая версия этого калькулятора находится здесь.
- Анимированное представление стоячих волн получаемых путём возбуждения длинной линии набором волн, состоящих из нескольких гармоник. Изменяется фаза и амплитуда гармоник, отношение длины линии к частоте, добротность.
- Производится подсчёт некоторых выходных параметров трансформатора Тесла при импульсном возбуждении. Результат выводится относительно первой гармоники из спектра полученных во вторичном контуре колебаний.
- Калькулятор расчитывает выходные параметры: действующее напряжение, рассеиваемую мощность и фазу напряжения, в зависимости от входного синусоидального напряжения для RC или RL цепи. Подсчитывается также и значение реактивного сопротивления — конденсатора или индуктивности — для заданной частоты.
- Калькулятор позволяет рассчитать параметры двухчастотной схемы последовательно-параллельного колебательного контура в онлайн. В нём возможен учёт ёмкости заземления и предусмотрены несколько режимов распределения волны в первичной катушке. Есть рекомендации для практической реализации устройства.
- Калькулятор позволяет найти оптимальную зависимость параметрического изменения индуктивности от тока, и рабочий режим возбуждающего генератора, для получения максимального КПД в замкнутой RL-цепи, где в качестве источника энергии выступает обратная ЭДС. Теоретическое обоснование получения дополнительной энергии из обратной ЭДС в катушке индуктивности с сердечником приводится здесь.
- Симулятор позволяет визуализировать некоторые процессы, которые происходят в радиоэлектронных схемах.
Программа распостраняется по свободной лицензии, как образовательная. Не рекомендуется использовать программу для моделирования реальных схем, так как многие компоненты в ней идеализированы.
Программа поддерживает следующие языки: Английский, Русский, Датский, Немецкий и Польский.
- Калькулятор предназначен для расчёта параметров различных схемотехнических решений усилителя тока.
Его расчёты основаны на комбинированных параметрических цепях первого и второго рода и довольно точно отражают происходящие там явления.
Также, калькулятор может применяться для исследования переходных процессов в параметрических и непараметрических RL-цепях.
Абонемент
| 2009-2020 © Vyacheslav Gorchilin |
Калькулятор
Программа «Калькулятор» представляет собой электротехнический калькулятор, позволяющий рассчитывать параметры колебательных контуров, определять индуктивности обособленных проводников и катушек различных типов, а также производить вычисления активных и реактивных сопротивлений. Помимо этого, в программу интегрирован поиск аналогов отечественных и зарубежных транзисторов и микросхем, а также модуль, содержащий справочные данные по SMD транзисторам и дающий возможность определять по цветовой маркировке номинал и класс точности резисторов и дросселей.
В меню «Расчёты» содержится три подпункта: «Колебательный контур», «Индуктивность» и «Сопротивление». В каждом из них, в свою очередь, можно выбрать необходимый шаблон для вычислений.
Шаблон для расчёта последовательного и параллельного колебательных контуров позволяет при задании резонансной частоты и ёмкости либо индуктивности определить недостающий параметр. При выборе расширенного режима расчёта контура дополнительно появляется возможность задать параметры волны, а также рассчитать физические параметры катушки индуктивности.
В подпункте «Индуктивность» можно выбрать шаблоны для расчёта габаритных параметров цилиндрических однослойных и многослойных катушек, дросселей на ферритовых кольцах и сердечниках, а также индуктивностей обособленных проводников. К примеру, в последнем случае задаются два из трёх параметров – длина проводника, диаметр его сечения и индуктивность, а третий рассчитывается автоматически. В остальных случаях расчёты производятся аналогичным образом.
В подпункте «Сопротивления» присутствуют два раздела: «Активное» и «Реактивное». В первом содержатся шаблоны для вычислений электрических параметров участка цепи по закону Ома, определения общего сопротивления двух параллельных резисторов, расчёта параметров добавочного сопротивления, делителя напряжения, шунтов, амперметров и вольтметров. Также есть возможность двустороннего пересчёта сопротивлений при соединении резисторов «звездой» и «треугольником». Во втором разделе присутствуют два шаблона: для расчёта реактивного сопротивления катушки индуктивности и конденсатора. Порядок и схема вычислений полностью идентичны описанным ранее.
В пункте меню «Маркировка» присутствует три раздела: «Сопротивления», «Дроссели» и «SMD транзисторы». В первых двух можно задать цвет и количество (для резисторов) маркировочных полос для определения номинала и класса точности элемента. Также доступна и обратная операция – при заданных параметрах программа изобразит цветовую маркировку на модели. Во вкладке «SMD транзисторы» открывается поисковик, осуществляющий выборку из базы данных всех элементов, соответствующих заданным критериям поиска.
Пункт «Аналоги» по-сути также представляет собой поисковики по базам данных микросхем и транзисторов. При этом производится выборка соответствий между компонентами отечественного и зарубежного производства.
Калькулятор совместим с Windows XP, Windows 7 x32/x64.
Распространение программы: Freeware (бесплатная)
Официальный сайт программы «Калькулятор»: http://calculator2006.narod.ru
Разработчик: Ivan219
Скачать Калькулятор
Обсуждение программы на форуме