Значение слова ЛЯМБДА. Что такое ЛЯМБДА?

• Λ, λ (название: ля́мбда, греч. λάμδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы — ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные.

Источник: Википедия

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова гайдук (существительное):

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

история и теория / Habr

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Термы:

переменная:	x
лямбда-абстракция (анонимная функция):	λx.t, где x — аргумент функции, t — её тело.
применение функции (аппликация):	f x, где f — функция, x — подставляемое в неё значение аргумента

Соглашения о приоритете операций:

• Применение функции левоассоциативно. Т.е. s t u — это тоже самое, что (s t) u
  
• Аппликация (применение или вызов функции по отношению к заданному значению) забирает себе всё, до чего дотянется. Т.е. λx. λy. x y x означает то же самое, что λx. (λy. ((x y) x))
  
• Скобки явно указывают группировку действий.

Может показаться, будто нам нужны какие-то специальные механизмы для функций с несколькими аргументами, но на самом деле это не так. Действительно, в мире чистого лямбда-исчисления возвращаемое функцией значение тоже может быть функцией. Следовательно, мы можем применить первоначальную функцию только к одному её аргументу, «заморозив» прочие. В результате получим новую функцию от «хвоста» аргументов, к которой применим предыдущее рассуждение. Такая операция называется

каррированием (в честь того самого Хаскелла Карри). Выглядеть это будет примерно так:

f = λx.λy.t	Функция с двумя аргументами x и y и телом t
f v w	Подставляем в f значения v и w
(f v) w	Эта запись аналогична предыдущей, но скобки явно указывают на последовательность подстановки
((λy.[x → v]t) w)	Подставили v вместо x. [x → v]t означает «тело t, в котором все вхождения x заменены на v»
[y → w][x → v]t	Подставили w вместо y. Преобразование закончено.

И напоследок несколько слов об области видимости. Переменная x называется связанной, если она находится в теле t λ-абстракции λx.t. Если же x не связана какой-либо вышележащей абстракцией, то её называют свободной. Например, вхождения x в x y и λy.x y свободны, а вхождения x в λx.x и λz.λx.λy.x(y z) связаны. В (λx.x)x первое вхождение x связано, а второе свободно. Если все переменные в терме связаны, то его называют замкнутым, или комбинатором. Мы с вами будем использовать следующий простейший комбинатор (функцию тождества): id = λx.x. Она не выполняет никаких действий, а просто возвращает без изменений свой аргумент.

Процесс вычисления

Рассмотрим следующий терм-применение:

(λx.t) y

Его левая часть — (λx.t) — это функция с одним аргументом

x и телом t. Каждый шаг вычисления будет заключаться в замене всех вхождений переменной x внутри t на y. Терм-применение такого вида носит имя редекса (от reducible expression, redex — «сокращаемое выражение»), а операция переписывания редекса в соответствии с указанным правилом называется бета-редукцией.

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

(λx.x) ((λx.x) (λz. (λx.x) z)),

который для простоты можно переписать как

id (id (λz. id z))

(напомним, что id — это функция тождества вида λx.x)

В этом терме содержится три редекса:

1. Полная β-редукция. В этом случае каждый раз редекс внутри вычисляемого терма выбирается произвольным образом. Т.е. наш пример может быть вычислен от внутреннего редекса к внешнему:
   
   
2. Нормальный порядок вычислений. Первым всегда сокращается самый левый, самый внешний редекс.
   
   
3. Вызов по имени. Порядок вычислений в этой стратегии аналогичен предыдущей, но к нему добавляется запрет на проведение сокращений внутри абстракции. Т.е. в нашем примере мы останавливаемся на предпоследнем шаге:
   
   Оптимизированная версия такой стратегии (вызов по необходимости) используется Haskell. Это так называемые «ленивые» вычисления.
   
4. Вызов по значению. Здесь сокращение начинается с самого левого (внешнего) редекса, у которого в правой части стоит значение — замкнутый терм, который нельзя вычислить далее.
   
   Для чистого лямбда-исчисления таким термом будет λ-абстракция (функция), а в более богатых исчислениях это могут быть константы, строки, списки и т.п. Данная стратегия используется в большинстве языков программирования, когда сначала вычисляются все аргументы, а затем все вместе подставляются в функцию.

Если в терме больше нет редексов, то говорят, что он вычислен, или находится в нормальной форме. Не каждый терм имеет нормальную форму, например (λx.xx)(λx.xx) на каждом шаге вычисления будет порождать самоё себя (здесь первая скобка — анонимная функция, вторая — подставляемое в неё на место x значение).

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

Ещё одна тонкость связана с именованием переменных. Например, терм (λx.λy.x)y после подстановки вычислится в λy.y. Т.е. из-за совпадения имён переменных мы получим функцию тождества там, где её изначально не предполагалось. Действительно, назови мы локальную переменную не y, а z — первоначальный терм имел бы вид(λx.λz.x)y и после редукции выглядел бы как λz.y. Для исключения неоднозначностей такого рода надо чётко отслеживать, чтобы все свободные переменные из начального терма после подстановки оставались свободными. С этой целью используют α-конверсию — переименование переменной в абстракции с целью исключения конфликтов имён.

Так же бывает, что у нас есть абстракция λx.t x, причём x свободных вхождений в тело t не имеет. В этом случае данное выражение будет эквивалентно просто t. Такое преобразование называется η-конверсией.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Список источников

1. «What is Lambda Calculus and should you care?», Erkki Lindpere
2. «Types and Programming Languages», Benjamin Pierce
3. Вики-конспект «Лямбда-исчисление»
4. «Учебник по Haskell», Антон Холомьёв
5. Лекции по функциональному программированию

Лямбда-точка — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 ноября 2015; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 ноября 2015; проверки требуют 5 правок.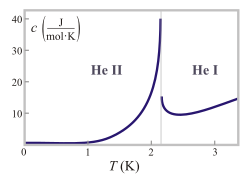 Лямбда-переход в жидком гелии: поведение удельной теплоёмкости при низких температурах

Лямбда-точка — температура (около 2,17 K), ниже которой жидкий гелий (гелий I), переходит в состояние сверхтекучести (гелий II).

Если быть более точным, существуют нижняя лямбда-точка (при 2,172 K и 0,0497 атм) и верхняя лямбда-точка (при 1,76 K и 29,8 атм).

Название происходит от специфического очертания графика удельной теплоёмкости как функции температуры (при постоянном давлении), напоминающее букву греческого алфавита λ. Удельная теплоёмкость имеет ярко выраженный пик по мере приближения температуры к лямбда-точке.

Ранние экспериментальные исследования теплоемкости^[1] привели к гипотезе, что она имеет логарифмическую особенность в лямбда-точке, и в частности стремится там в бесконечность. Более точные эксперименты^[2][3] опровергли эту гипотезу, которую к сожалению еще можно встретить в университетских учебниках.^[4] В настоящее время надежно установлено,^[5] что поведение теплоемкости вблизи лямбда-точки описывается формулой C≈A±t−α+B±{\displaystyle C\approx A_{\pm }t^{-\alpha }+B_{\pm }}, где t=|1−T/Tc|{\displaystyle t=|1-T/T_{c}|} есть приведенная температура, Tc{\displaystyle T_{c}} температура лямбда-точки, A±,B±{\displaystyle A_{\pm },B_{\pm }} константы принимающие различные значения выше и ниже точки перехода, а α≈−0.01{\displaystyle \alpha \approx -0.01} критический индекс. Так как этот индекс имеет отрицательное значение для перехода в сверхтекучее состояние, теплоемкость в лямбда-точке имеет конечные (хотя и большие) пределы при приближении с низких и высоких температур .^[6]

1. ↑ C. Buckingham and W.H. Fairbank. The Nature of the Lambda-Transition in Liquid Helium // Progress in Low Temperature Physics, vol. 3. — Amsterdam: North-Holland, 1961.
2. ↑ Guenther Ahlers. Heat Capacity at Constant Pressure near the Superfluid Transition in He 4 (англ.) // Physical Review Letters. — 1969-09-01. — Vol. 23, iss. 9. — P. 464—468. — ISSN 0031-9007. — DOI:10.1103/PhysRevLett.23.464.
3. ↑ K. H. Mueller, Guenter Ahlers, F. Pobell. Thermal expansion coefficient, scaling, and universality near the superfluid transition of He 4 under pressure (англ.) // Physical Review B. — 1976-09-01. — Vol. 14, iss. 5. — P. 2096—2118. — ISSN 0556-2805. — DOI:10.1103/PhysRevB.14.2096.
4. ↑ Квасников И.А. Термодинамика и статистическая физика. Том 1: Теория равновесных систем: Термодинамика. Учебное пособие. — Изд. 2-е, сущ. перераб. и доп.. — Москва: Едиториал УРСС, 2002. — С. 119. — 240 с. — ISBN 5-354-00077-7.
5. ↑ Lipa, J.A.; Swanson, D. R.; Nissen, J. A.; Chui, T. C. P.; Israelsson, U. E. Heat Capacity and Thermal Relaxation of Bulk Helium very near the Lambda Point (англ.) // Physical Review Letters : journal. — 1996. — Vol. 76, no. 6. — P. 944—947. — DOI:10.1103/PhysRevLett.76.944. — Bibcode: 1996PhRvL..76..944L. — PMID 10061591.
6. ↑ Теплоемкость обращается в бесконечность только для фазовых переходах второго рода с положительным индексом α{\displaystyle \alpha }. Например, это просиходит в критической точке жидкость-пар, которая имеет изинговские критические индексы.

Пардон, а что такое ЛЯМБДА???

11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30

Символ, в физике обозначает длину волны.

греческая буковка (Λ, λ)

Λ, λ (название: ля́мбда, греч. λάμδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы — ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные. Прописная Λ Использовалась в качестве узора на щитах в спартанской армии, обозначая Лакедемон Используется в некоторых шрифтах вместо Л используется Λ (например Franklin Gothic.) Космологическая постоянная Ламбда-частицы в физике частиц В спектральном разложении матрицы — диагональная матрица из собственных значений раскладываемой матрицы Выражения типов в типизированном ламбда-исчислении В математике — частое обозначение для вновь вводимых операторов. [править] Строчная λ λ-зонд — датчик кислорода Собственные значения в линейной алгебре Длина волны в физике Функциональные выражения в лямбда-исчислении, в функциональном программировании и языках программирования Постоянная распада — вероятность распада ядра в единицу времени (связана с периодом полураспада радиоактивного изотопа в физике) Фаг ламбда — вирус-бактериофаг в биологии Удельная теплота плавления в физике Удлинение крыла в самолетостроении

Отслеживает стехиометрический состав смеси.

Датчик кислорода конечно. Не заморачивайтесь если бы лямда полетел бы расход за 15 вырос бы.

Буква греческоко алфавита, в физике применяется для обозначения длины волны)

Лямбда — буква греческого алфавита. Лямбда — отношение реального количества воздуха в горючей смеси к оптимальному. Лямбда-зонд — датчик в выходном коллекторе двигателя, определяющий количество кислорода в выхлопных газах.

лямбда-зонд, иначе еще называют кислородным датчиком установлен в выхлопном тракте, отслеживает содержание кислорода в выхлопных газах

Ты про лямбда зонд имеешь ввиду? На почитай: <a rel=»nofollow» href=»http://www.autoshcool.ru/1564-lyambda-zond-princip-raboty.html» target=»_blank»>http://www.autoshcool.ru/1564-lyambda-zond-princip-raboty.html</a> Нормальный у тебя расход не парься, если дело было бы в лямбда зонде, то жрала бы она у тебя не 10 литров, а 25!!!

ха ха ха блин /// зонт такой от потока бензина

черепаху так зовут, епть, мою.

λ Это значок из Half Life XD

Халф — Лайф! Блэт λ

11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы — ламд.

лямбда-обозначение — Викисловарь

Содержание

• 1 Русский
  • 1.1 Морфологические и синтаксические свойства
  • 1.2 Произношение
  • 1.3 Семантические свойства
    • 1.3.1 Значение
    • 1.3.2 Синонимы
    • 1.3.3 Антонимы
    • 1.3.4 Гиперонимы
    • 1.3.5 Гипонимы
  • 1.4 Родственные слова
  • 1.5 Этимология
  • 1.6 Фразеологизмы и устойчивые сочетания
  • 1.7 Перевод
  • 1.8 Библиография

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	ля́мбда-обозначе́ние	ля́мбда-обозначе́ния
Р.	ля́мбда-обозначе́ния	ля́мбда-обозначе́ний
Д.	ля́мбда-обозначе́нию	ля́мбда-обозначе́ниям
В.	ля́мбда-обозначе́ние	ля́мбда-обозначе́ния
Тв.	ля́мбда-обозначе́нием	ля́мбда-обозначе́ниями
Пр.	ля́мбда-обозначе́нии	ля́мбда-обозначе́ниях

ля́м-бда-о·бо-зна-че́-ни·е

Существительное, неодушевлённое, средний род, 2-е склонение (тип склонения 7a по классификации А. А. Зализняка).

Корень: —.

Произношение[править]

• МФА: [ˌlʲambdə ɐbəznɐˈt͡ɕenʲɪɪ̯ə]

Семантические свойства[править]

Значение[править]

1. ◆ Отсутствует пример употребления (см. рекомендации).
2. ◆ Отсутствует пример употребления (см. рекомендации).

Синонимы[править]

Антонимы[править]

Гиперонимы[править]

Гипонимы[править]

Родственные слова[править]

Ближайшее родство

Этимология[править]

Происходит от ??

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Список переводов

Библиография[править]

Для улучшения этой статьи желательно: Добавить описание морфемного состава с помощью {{морфо-ru}} Добавить значение в секцию «Семантические свойства» Добавить синонимы в секцию «Семантические свойства» Добавить гиперонимы в секцию «Семантические свойства» Добавить сведения об этимологии в секцию «Этимология» Добавить хотя бы один перевод в секцию «Перевод»

исчисление — это… Что такое Лямбда-исчисление?

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.

λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию. λ-исчисление реализовано Джоном Маккарти в языке Лисп. Вначале реализация идеи λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.

Чистое λ-исчисление

Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами (обами), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличия каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если  — выражение, свободно содержащее , тогда запись означает: функция от аргумента , которая имеет вид , обозначает функцию . Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы свободно входило в , не очень существенно — достаточно предположить, что , если это не так.

β-редукция

Поскольку выражение обозначает функцию, ставящую в соответствие каждому значение , то для вычисления выражения

,

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм вместо переменной . В результате получается . Это соображение в общем виде записывается как

и носит название β-редукция. Выражение вида , то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

η-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применённые к любому аргументу, дают одинаковые результаты. η-преобразование переводит друг в друга формулы и (в обратную сторону — только если не имеет свободных вхождений в : иначе свободная переменная после преобразования станет связанной внешней абстракцией).

Функция двух переменных и может быть рассмотрена как функция одной переменной , возвращающая функцию одной переменной , то есть как выражение . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D → D до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n — 1).

В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого, аргумент, ссылающийся на себя (здесь обозначен как r), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз. Так как существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))

В лямбда-исчислении, Y g — неподвижная точка g; продемонстрируем это:

Y g

λh.((λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g).

Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g) n, где n — число, для которого вычисляется факториал. Пусть n = 4, получаем:

   g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции.

См. также

Примечания

1. ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.
• Чечулин В. Л. О непротиворечивости лямбда-исчисления // В мире научных открытий, серия Математика. Механика. Информатика, 2011, № 1, сс. 203—206

ВСЁ ПРО ЛЯМБДУ

Датчик кислорода предназначен для определения концентрации кислорода в отработавших газах, состав которых зависит от соотношения топлива и воздуха в смеси, подаваемой в цилиндры двигателя. Информация, которую выдает датчик в виде напряжения (или изменения сопротивления), используется электронным блоком управления впрыском (или карбюратором) для корректировки количества подаваемого топлива. Для полного сгорания 1 кг топлива необходимо 14,7 кг воздуха. Такой состав топливо-воздушной смеси называют стехиометрическим, он обеспечивает наименьшее содержание токсичных веществ в отработавших газах и, соответственно, эффективное их «дожигание» в каталитическом нейтрализаторе. Для оценки состава топливо-воздушной смеси используют коэффициент избытка воздуха — отношение количества воздуха, поступившего в цилиндры, к количеству воздуха, теоретически необходимого для полного сгорания топлива. В мировой практике этот коэффициент называют лямбда. При стехиометрической смеси лямбда = 1, если лямбда < 1 (недостаток воздуха), смесь называют богатой, при лямбда >1 (избыток воздуха) смесь называют бедной. Наибольшая экономичность при полностью открытой дроссельной заслонке бензинового двигателя достигается при лямбда=1,1-1,3. Максимальная мощность обеспечивается, когда лямбда =0,85-0,9. Общие сведения В справочной литературе датчик может называться по-разному: кислородный датчик, регулятор «лямбда», лямбда-зонд, датчик концентрации кислорода в отработавших газах. Кислородные датчики бывают двух типов: электрохимические и резистивные. Первый тип датчиков работает по принципу элемента, вырабатывающего электрический ток. Второй — работает, как резистор, изменяя свое сопротивление от условий среды, в которой находится. Наибольшее распространение в настоящее время получили электрохимические датчики кислорода. В них используется свойство диоксида циркония создавать разность электрических потенциалов (напряжение) при разной концентрации кислорода (в отработавших газах и окружающем воздухе). При нормальной работе системы подачи топлива напряжение, вырабатываемое датчиком кислорода, может изменяться несколько раз в секунду. Это позволяет приготавливать и поддерживать необходимый состав топливной смеси практически на любом режиме работы двигателя. Устройство датчика кислорода. Устройство датчика кислорода: 1- металлический корпус с резьбой. 2 — уплотнительное кольцо.c 3 — токосъемник электрического сигнала. 4 — керамический изолятор. 5 — проводка. 6 — манжета проводов уплотнительная. 7 — токопроводящий контакт цепи подогрева. 8 — наружный защитный экран с отверстием для атмосферного воздуха. 9 — подогрев. 10 — наконечник из керамики. 11 — защитный экран с отверстием для отработавших газов. Основная часть датчика — керамический наконечник, сделанный на основе диоксида циркония, на внутреннюю и наружную поверхности которого методом напыления наносится платина. Соединение наконечника и корпуса выполнено полностью герметичным во избежание попадания отработавших газов во внутреннюю полость датчика, сообщающуюся с атмосферой. Керамический наконечник находится в потоке отработавших газов, поступающих через отверстия в защитном экране. Эффективная работа датчика возможна при температуре не ниже 300-350’С. Поэтому, для быстрого прогрева после пуска двигателя, современные датчики снабжают электрическим нагревательным элементом, представляющим из себя керамический стержень со спиралью накаливания внутри. Датчики кислорода с различным количеством проводов: провод сигнала, провод «массы» сигнала, провод питания подогрева, провод «массы» подогрева. Датчики без нагревателя могут иметь один, или два сигнальных провода, датчики со встроенным электрическим нагревателем — три или четыре провода. Как правило, провода светлых цветов относятся к нагревателю, а темных — к сигнальному проводу. Все элементы датчика кислорода изготовлены из жаростойких материалов, так как его рабочая температура может достигать 950°С. Выходящие провода имеют термостойкую изоляцию. Место установки датчика кислорода. В связи с тем, что датчик кислорода может вырабатывать электрический сигнал только при температуре 300-350°С и выше, датчики без нагревателя устанавливаются в выпускном трубопроводе ближе к двигателю, а с нагревательными элементами — перед нейтрализатором. В некоторых автомобилях в каталитическом нейтрализаторе установлен датчик температуры, который не следует путать с кислородным. Иногда устанавливается два кислородных датчика — до нейтрализатора

Примечание. Присоединительные разъемы и длина проводов у некоторых датчиков кислорода могут не совпадать. Маркировка датчиков: На каждом датчике кислорода, как правило, обозначено: наименование страны-изготовителя; наименование и (или) товарный знак изготовителя; условное обозначение типа. Ресурс и периодичность контроля работоспособности Датчики кислорода имеют неразборную конструкцию и не требуют обслуживания. Ресурс электрохимических датчиков кислорода составляет от 60 до 80 тыс. км пробега автомобиля при соблюдении условий эксплуатации, нарушение которых резко сокращает срок службы. Рекомендуется проверять датчики кислорода при каждом техническом обслуживании автомобиля. Причины преждевременного выхода из строя датчика кислорода 1. Применение этилированного бензина или несоответствующей марки топлива. 2. Использование при установке датчика герметиков, вулканизирующихся при комнатной температуре или содержащих в своем составе силикон. 3. Перегрев датчика из-за неправильно установленного угла опережения зажигания, переобогащения топливо-воздушной смеси, перебоев в зажигании и т. д. 4. Многократные (неудачные) попытки запуска двигателя через небольшие промежутки времени, что приводит к накапливанию несгоревшего топлива в выпускном трубопроводе, которое может воспламениться с образованием ударной волны. 5. Проверка работы цилиндров двигателя с отключением свечей зажигания. 6. Попадание на керамический наконечник датчика любых эксплуатационных жидкостей, растворителей и моющих средств. 7. Обрыв, плохой контакт или замыкание на «массу» выходной цепи датчика. 8. Негерметичность в выпускной системе. Возможные признаки неисправности датчика кислорода 1. Неустойчивая работа двигателя на малых оборотах. 2. Повышенный расход топлива. 3. Ухудшение динамических характеристик автомобиля. 4. Характерное потрескивание в районе расположения каталитического нейтрализатора после остановки двигателя. 5. Повышение температуры в районе каталитического нейтрализатора или его нагрев до раскаленного состояния. 6. На некоторых автомобилях загорание лампы «СНЕСК ЕNGINЕ» при установившемся режиме движения. Правила снятия и установки датчика 1. Демонтаж датчика, во избежание повреждений, производят только на холодном двигателе, перед этим отсоединяют провода датчика (при выключенном зажигании). 2. Перед заменой датчика необходимо проверить его маркировку, которая должна соответствовать указанной в инструкции по эксплуатации автомобиля. 3. Производят внешний осмотр, чтобы: o убедиться в отсутствии механических повреждений; o проверить наличие уплотнительного кольца; o проверить наличие на резьбовой части специальной противопригарной смазки. 4. Заворачивают от руки датчик кислорода до упора и затягивают с усилием 3,5-4,5 кгм. Соединение должно быть герметичным. 5. Соединяют электрический разъем (разъемы). 6. Проверяют работоспособность по контролируемым параметрам. В некоторых случаях датчик крепится к выпускному трубопроводу с помощью специальной пластины. Между пластиной и выпускным трубопроводом должна находиться специальная герметизирующая прокладка. Основные контролируемые параметры Проверка параметров датчика кислорода осуществляется при достижении им рабочей температуры (350+50°С) с использованием газоанализатора, осциллографа, цифрового вольтметра и омметра. Контролируются следующие параметры: 1. при значении Лямбда=0,9 (обогащенная горючая смесь) напряжение на сигнальном проводе должно быть не менее 0,65 В; 2. при значении лямбда=1,1 (обедненная горючая смесь) напряжение на сигнальном выводе должно быть не более 0,25 В; 3. время срабатывания при обедненной горючей смеси — не более 250 мс; 4. время срабатывания при обогащенной горючей смеси — не более 450 мс; 5. сопротивление при температуре 350 + 50 «С не более 10кОм. Бензиновому двигателю для работы требуется смесь с определенным соотношением воздух-топливо. Соотношение, при котором топливо максимально полно и эффективно сгорает, называется стехиометрическим и составляет оно 14,7:1. Это означает, что на одну часть топлива следует взять 14,7 частей воздуха. На практике же соотношение воздух-топливо меняется в зависимости от режимов работы двигателя и смесеобразования. Двигатель становится неэкономичным. Это и понятно!

Коэффициент избыточности воздуха — L (лямбда) характеризует — насколько реальная топливно-воздушная смесь далека от оптимальной (14,7:1). Если состав смеси — 14,7:1, то L=1 и смесь оптимальна. Если L < 1, значит недостаток воздуха, смесь обогащенная. Мощность двигателя увеличивается при L=0,85 — 0,95. Если L > 1, значит налицо избыток воздуха, смесь бедная. Мощность при L=1,05 — 1,3 падает, но зато экономичность растет. При L > 1,3 смесь перестает воспламеняться и начинаются пропуски в зажигании. Бензиновые двигатели развивают максимальную мощность при недостатке воздуха в 5-15% (L=0,85 — 0,95), тогда как минимальный расход топлива достигается при избытке воздуха в 10-20%% (L=1,1 — 1,2). Таким образом соотношение L при работе двигателя постоянно меняется и диапазон 0,9 — 1,1 является рабочим диапазоном лямбда-регулирования. В то же время, когда двигатель прогрет до рабочей температуры и не развивает большой мощности (например работает на ХХ), необходимо по возможности более строгое соблюдение равенства L=1 для того, чтобы трехкомпонентный катализатор смог полностью выполнить свое предназначение и сократить объем вредных выбросов до минимума.

Датчик кислорода — он же лямбда-зонд — устанавливается в выхлопном коллекторе таким образом, чтобы выхлопные газы обтекали рабочую поверхность датчика. Материал его как правило циркониевый (используется керамический элемент на основе двуокиси циркония, покрытый платиной) — гальванический источник тока, меняющий напряжение в зависимости от температуры и наличия кислорода в окружающей среде. Конструкция его предполагает, что одна часть соединяется с наружним воздухом, а другая — с выхлопными газами внутри трубы. В зависимости от концентрации кислорода в выхлопных газах, на выходе датчика появляется сигнал. Уровень этого сигнала, для датчиков систем впрыска конца 80-х — начала 90-х годов, может быть низким (0,1…0,2В) или высоким (0,8…0,9В). Таким образом датчик кислорода — это своеобразный переключатель (триггер), сообщающий контроллеру впрыска о качественной концентрации кислорода в отработавших газах. Фронт сигнала между положениями «Больше» и «меньше» очень мал. Настолько мал, что его можно не рассматривать всерьез. Контроллер принимает сигнал с ЛЗ, сравнивает его с значением, прошитым в его памяти и, если сигнал отличается от оптимального для текущего режима, корректирует длительность впрыска топлива в ту или иную сторону. Таким образом осуществляется обратная связь с контроллером впрыска и точная подстройка режимов работы двигателя под текущую ситуацию с достижением максимальной экономии топлива и минимизацией вредных выбросов.

Лямбда-зонды бывают одно-, двух-, трех- и четырехпроводные. Однопроводные и двухпроводные датчики применялись в самых первых системах впрыска с обратной связью (лямбда-регулированием). Однопроводный датчик имеет только один провод, который является сигнальным. Земля этго датчика выведена на корпус и приходит на массу двигателя через резьбовое соединение. Двухпроводный датчик отличается от однопроводного наличием отдельного земляного провода сигнальной цепи. Недостатки таких зондов: рабочий диапазон температуры датчика начинается от 300 градусов. До достижения этой температуры датчик не работает и не выдает сигнала. Стало быть необходимо устанавливать этот датчик как можно ближе к цилиндрам двигателя, чтобы он подогревался и обтекался наиболее горячим потоком выхлопных газов. Процесс нагрева датчика затягивается и это вносит задержку в момент включения обратной связи в работу контроллера. Кроме того, использование самой трубы в качестве проводника сигнала (земля) требует нанесения на резьбу специальной токопроводящей смазки при установке датчика в выхлопной трубопровод и увеличивает вероятность сбоя (отсутствия контакта) в цепи обратной связи. Указанных недостатков лишены трех- и четырехпроводные лямбда зонды. В трехпроводный ЛЗ добавлен специальный нагревательный элемент, который включен как правило всегда при работе двигателя и, тем самым, сокращает время выхода датчика на рабочую температуру. А так же позволяет устанавливать лямбда-зонд на удалении от выхлопного коллектора, рядом с катализатором. Однако остается один недостаток — токопроводящий выхлопной коллектор и необходимость в токопроводящей смазке.

Этого недостатка лишен четырехпроводный лямбда-зонд — у него все провода служат для своих целей — два на подогрев, а два — сигнальные. При этом вкручивать его можно так как заблагорассудится. Несколько слов о взаимозаменяемости датчиков. Лямбда-зонд с подогревом может устанавливаться вместо такого же, но без подогрева. При этом необходимо смонтировать на автомобиль цепь подогрева и подключить ее к цепи, запитываемой при включении зажигания. Самое выгодное — в параллель к цепи питания электробензонасоса. Не допускается обратная замена — установка однопроводного датчика вместо трех- и более- проводных. Работать не будет. Ну и конечно необходимо, чтобы резьба датчика совпадала с резьбой, нарезанной в штуцере.

Как понять насколько работоспособен датчик? Ввобще-то для этого потребуется осциллограф. Ну или специальный мотор-тестер, на дисплее которого можно наблюдать осциллограмму изменения сигнала на выходе ЛЗ. Наиболее интересными являются пороговые уровни сигналов высокого и низкого напряжения (со временем, при выходе датчика из строя, сигнал низкого уровня повышается (более 0,2В — криминал), а сигнал высокого уровня — снижается (менее 0,8В — криминал)), а также скорость изменения фронта переключения датчика из низкого в высокий уровень. Есть повод задуматься о предстоящей замене датчика, если длительность этого фронта превышает 300 мсек. Это усредненные данные. В реальной жизни для оценки состояния лямбда-зонда необходимо провести цикл измерений. Не имея под рукой мотор-тестера или осциллографа определить неисправность лямбда-зонда можно пользуясь бортовой системой диагностики, существующей в контроллере системы впрыска, которая фиксирует в своей памяти случаи, когда сигнал с ЛЗ выходил за определенные пределы. Фиксация неисправностей производится при помощи запоминания специальных кодов, которые могут быть считаны в тестовом режиме. Однако не всегда можно с уверенностью поставить четкий диагноз о неисправности лямбда-зонда пользуясь только бортовой системой диагностики. Об этом стоит помнить! Не поленитесь съездить на диагностику. Но в некоторых случаях можно с большой степенью уверенности утверждать, что лямбда-зонд вышел из строя и подлежит замене.

На что менять? Самое лучшее — это менять датчик на такой, какой стоит в списке запчастей для Вашего автомобиля. В таком случае гарантия работоспособности системы после замены будет 100%. Но не всегда по финансовым соображениям выгодно гоняться за оригинальными каталожными датчиками. Ведь тот же Bosch выпускает лямбда-датчики и для других моделей. И они по принципу работы одинаковы, а внешне очень похожи. Ну и что, что каталожный номер будет стоять другой. При правильной установке и грамотном подборе можно съэкономить весьма кругленькую сумму, купив «жигулевский» датчик от фирмы Bosch за 10-20$ вместо точно такого же по сути, но фирменного за 100$ и работать он будет ничуть не хуже. Найти ЛЗ в магазине сейчас можно все чаще и чаще, а значит они будут дешеветь.

Для ничего не соображающих в данном вопросе можно сразу написать взаимозаменяемость датчиков кислорода: • Вместо родного трехпроводного датчика BOSCH O 258 003 021, стоявшего на машине я поставил без каких либо проблем четырехпроводный «жигулевский» BOSCH O 258 005 133.

Итак: Вы походили по магазинам и купили заветный кусочек металла с проводами…

Внимание: Кислородный датчик содержит очень хрупкие керамические ячейки. Во избежание повреждения новый ЛЗ не следует ронять, стучать по нему…

Порядок замены ЛЗ таков: • Отсоединить кабель ЛЗ от электропроводки. • Снять старый ЛЗ используя подходящий ключ. Лучше если это будет высокая головка или накидной — так вероятность повредить грани приржавленного ЛЗ будет меньше, но у меня нормально открутился на работающем моторе накидным ключом. Снимать датчик стоит при работающем двигателе. Т.е. пока трубопровод и датчик горячий. В противном случае есть вероятность отломать датчик или сорвать резьбу, т.к. металл сжимается и выворачивать очень трудно. Выкручивайте датчик до тех пор, пока из отверстия не пойдет дымок. Потом глушите машину и откручивайте совсем. • Отрезать аккуратно провода от старого ЛЗ и соединить с проводами нового, которые тоже придется отрезать от колодки. Схема соединения зависит от того — какой ЛЗ Вы купили. Но обычные цвета и предназначение проводов даны чуть выше, на картинках. • Следует иметь ввиду, что если штатный лямбда-зонд трехпроводный, то у него провода подписаны (см. на разъеме) «А» и «Б» — подогрев, «С» — сигнальный. Провода подогрева белого цвета (полярность не имеет значения), а сигнальный провод — черный. • Четвертый (незадействованный ранее) провод стоит вывести и надежно прикрутить к массе двигателя. Проверить также соединение двигателя с массой корпуса. Я прикрутил его под болт крепления главного тормозного цилиндра (в торце кронштейн) — мне так показалось удобнее. • Вкрутить новый ЛЗ. Если он четырехпроводный, то токопроводящая смазка не нужна. Достаточно графитовой — для смазки резьбовых соединений. • Соединение проводов не стоит осуществлять скруткой проводов — этот вариант ненадежен и долго не проживет. Самое лучшее — это спаять все положенные провода и хорошенько заизолировать. Паять провода стоит до того, как ЛЗ установлен в трубе, т.е. на столе. • После замены рекомендую обнулить память контроллера путем снимания на несколько секунд (-)клеммы с аккумулятора. Только подумайте предварительно — не отключатся ли у вас какие нибудь электроприборы типа магнитол, CD-чейнджеров и пр. и не встанут ли они после этого на код. Это важно.

                                                          СХЕМА ЭМУЛЯТОРА

Иногда при диагностике и ремонте системы впрыска возникает необходимость в имитации сигнала лямбда-зонда (например, чтобы убедиться в правильности работы кодовой само- и диагностики), и тут без эмулятора не обойтись. Некоторые фирменные имитаторы датчиков содержат функцию такой эмуляции. Однако далеко не все инжекторщики оснащены фирменными приборами в силу их непомерно высокой стоимости. В то же время несложно самому изготовить простой эмулятор, причем возможных вариантов изготовления немало. Один из таких вариантов приводится ниже. Принцип работы. На микросхеме собран мультивибратор инфранизкой частоты, значение которой определяется RC-цепочкой и регулируется переменным резистором в пределах 0,3…30 Гц (типичное значение частоты лямбда-зонда 0,5…2 Гц). При указанных на схеме номиналах генерируется частота 0,5 Гц. Что показано на осциллограмме. Эмиттерный повторитель на транзисторе служит для исключения влияния последующих цепей на работу мультивибратора. Выходная RC-цепочка определяет крутизну фронтов и форму вершин выходного сигнала. Два встречно-параллельных диода ограничивают сигнал по амплитуде, а нижний диод совместно с резистором обеспечивает такое смещение, при котором сигнал все время остается положительным. Выходной делитель напряжения на двух резисторах имитирует нагрузку лямбда-зонда и обеспеччивает требуемую амплитуду выходного сигнала. При указанных на схеме номиналах амплитуда сигнала изменяется от 0,1 до 0,9 В. Питание эмулятора обеспечивается от бортовой системы автомобиля или от другого источника. При необходимости с выхода OUT микросхемы могут быть сняты прямоугольные импульсы той же частоты. Детали. Микросхема – таймер. Транзистор и диоды – любые кремниевые маломощные среднечастотные. Постоянные резисторы любого типа мощностью 0,125 Вт. Настройка. Правильно собранный эмулятор в настройке практически не нуждается. Вы можете предварительно протестировать схему с помощью программы Electronics Workbench. Приведенные рисунки — из EWB версии 5.12. Эмулятор подключается вместо штатного лямбда-зонда в точке, где на рисунке указано подключение осциллографа. В зависимости от величины входного сопротивления контроллера системы впрыска адаптация к нему может заключаться в следующем: отключение резистора R7 или увеличение его сопротивления, а также подбор сопротивления R6, чтобы сигнал эмулятора изменялся в пределах 0,1-0,15…0.8-0,9 В. Принцип работы. На микросхеме собран мультивибратор инфранизкой частоты, значение которой определяется RC-цепочкой и регулируется переменным резистором в пределах 0,3…30 Гц (типичное значение частоты лямбда-зонда 0,5…2 Гц). При указанных на схеме номиналах генерируется частота 0,5 Гц. Что показано на осциллограмме. Эмиттерный повторитель на транзисторе служит для исключения влияния последующих цепей на работу мультивибратора. Выходная RC-цепочка определяет крутизну фронтов и форму вершин выходного сигнала. Два встречно-параллельных диода ограничивают сигнал по амплитуде, а нижний диод совместно с резистором обеспечивает такое смещение, при котором сигнал все время остается положительным. Выходной делитель напряжения на двух резисторах имитирует нагрузку лямбда-зонда и обеспеччивает требуемую амплитуду выходного сигнала. При указанных на схеме номиналах амплитуда сигнала изменяется от 0,1 до 0,9 В. Питание эмулятора обеспечивается от бортовой системы автомобиля или от другого источника. При необходимости с выхода OUT микросхемы могут быть сняты прямоугольные импульсы той же частоты. Детали. Микросхема – таймер. Транзистор и диоды – любые кремниевые маломощные среднечастотные. Постоянные резисторы любого типа мощностью 0,125 Вт. Настройка. Правильно собранный эмулятор в настройке практически не нуждается. Вы можете предварительно протестировать схему с помощью программы Electronics Workbench. Приведенные рисунки — из EWB версии 5.12. Эмулятор подключается вместо штатного лямбда-зонда в точке, где на рисунке указано подключение осциллографа. В зависимости от величины входного сопротивления контроллера системы впрыска адаптация к нему может заключаться в следующем: отключение резистора R7 или увеличение его сопротивления, а также подбор сопротивления R6, чтобы сигнал эмулятора изменялся в пределах 0,1-0,15…0.8-0,9 В.

Другой вариант эмулятора показан на рисунке ниже. Преимущество этой схемы заключается в том, что она более проста и менее зависима от входного сопротивления контроллера системы впрыска. Недостаток – менее закруглена вершина сигнала, что менее существенно. Настройка сводится к подбору резисторов так, чтобы длительность сигналов 0,1 и 0,9 В была примерно одинаковой. Адаптация к контроллеру аналогична первой схеме и заключается в подборе сопротивлений выходного делителя. 

                                                                  СХЕМА

Полный текст находится в файловом  архиве  тут. Всё про Лямбду и Эмуляторы.exe 

 КАТАЛОГ lambda_sensors_2010_2011_ru.pdf

 

 

                   

 

                                                                   НАВЕРХ