Схождение и развал колес подробно — Энциклопедия журнала «За рулем»
Зачем нужны углы развала, схождения и кастер?
Подвеска без углов
Если вообще не делать никаких углов, колесо в ходе сжатия-отбоя будет оставаться перпендикулярным к дороге, в постоянном и надежном контакте с ней. Правда, совместить центральную плоскость вращения колеса и ось его поворота конструктивно довольно сложно (здесь и далее речь о классической двухрычажной подвеске заднеприводного автомобиля, например «жигулей»), поскольку обе шаровые опоры вкупе с тормозным механизмом внутрь колеса не помещаются. А раз так, то плоскость и ось «расходятся» на расстояние А, называемое плечом обката (при повороте колесо обкатывается вокруг оси ab). В движении сила сопротивления качению неведущего колеса создает на этом плече ощутимый момент, скачкообразно меняющийся при проезде неровностей. В результате руль будет постоянно рваться из рук.
В поперечной плоскости положение колеса характеризуется углами α (развал) и β(наклон оси поворота)
Кроме того, преодолевать этот самый немалый момент в повороте придется мускульной силой. Стало быть, положительное (в данном случае) плечо обката желательно уменьшить, а то и вовсе свести к нулю. Для этого можно наклонить ось поворота ab. Здесь важно не переусердствовать, чтобы при ходе вверх колесо не слишком заваливалось внутрь.
Стало быть, положительное (в данном случае) плечо обката желательно уменьшить, а то и вовсе свести к нулю. Для этого можно наклонить ось поворота ab. Здесь важно не переусердствовать, чтобы при ходе вверх колесо не слишком заваливалось внутрь.
Качение наклонного колеса напоминает качение конуса
На практике делают так: несколько наклонив ось поворота (β), нужную величину добирают наклоном плоскости вращения колеса (α). Угол ос и есть развал. Под этим углом колесо опирается о дорогу. Покрышка в зоне контакта деформируется.
Выходит, что автомобиль движется словно на двух конусах, стремящихся раскатиться в стороны. Чтобы компенсировать эту неприятность, плоскости вращения колес надо свести. Процесс называется регулировкой схождения. Оба параметра жестко связаны. То есть, если угол развала нулевой, не должно быть и схождения, отрицательный — требуется расхождение, иначе шины будут «гореть». Если на автомобиле развал колес выставлен по-разному, его будет тянуть в сторону колеса с большим наклоном.
При положительном плече обката поворот колеса сопровождается подъемом передка кузова
Другие два угла обеспечивают стабилизацию управляемых колес — проще говоря, заставляют автомобиль с отпущенным рулем ехать прямо. Угол поперечного наклона оси поворота (β) отвечает за весовую стабилизацию. Легко заметить, что при этой схеме (рис.) в момент отклонения колеса от «нейтрали» передок начинает подниматься. А так как весит он немало, то при отпускании руля под действием силы тяжести система стремится занять исходное положение, соответствующее движению по прямой. Правда, для этого приходится сохранять то самое, хоть и небольшое, но нежелательное положительное плечо обката.
Кастер — угол продольного наклона оси поворота
Продольный угол наклона оси поворота — кастер — дает динамическую стабилизацию. Принцип ее ясен из поведения рояльного колесика — в движении оно стремится оказаться позади ножки, то есть занять наиболее устойчивое положение. Чтобы получить тот же эффект в автомобиле, точка пересечения оси поворота с поверхностью дороги (с) должна быть впереди центра пятна контакта колеса с дорогой (d). Для этого ось поворота и наклоняют вдоль…
Чтобы получить тот же эффект в автомобиле, точка пересечения оси поворота с поверхностью дороги (с) должна быть впереди центра пятна контакта колеса с дорогой (d). Для этого ось поворота и наклоняют вдоль…
Так «работает» кастер
…Теперь при повороте боковые реакции дороги, приложенные позади … (спасибо кастеру!) стараются вернуть колесо на место.
Более того, если на машину действует боковая сила, не связанная с поворотом (например, вы едете по косогору
или при боковом ветре), то кастер обеспечивает при случайно отпущенном руле плавный поворот машины «под склон» или «под ветер» и не дает ей опрокинуться.
Положительное (а) и отрицательное (б) плечи обката
В переднеприводном автомобиле с подвеской «Мак-Ферсон» ситуация совершенно иная. Эта конструкция позволяет получить нулевое и даже отрицательное (рис. б) плечо обката — ведь внутрь колеса здесь надо «запихнуть» лишь опору единственного рычага. Угол развала (и, соответственно, схождения) легко свести к минимуму. Так и есть: ВАЗов «восьмого» семейства развал — 0°±30′, схождение — 0±1 мм. Так как передние колеса теперь тянут автомобиль, динамическая стабилизация при разгоне не требуется — колесо уже не катится позади ножки, а тянет ее за собой. Небольшой (1°30′) угол продольного наклона оси поворота сохранен для устойчивости при торможении. Значительный вклад в «правильное» поведение автомобиля вносит отрицательное плечо обката — при возрастании сопротивления качению колеса оно автоматически корректирует траекторию.
Так и есть: ВАЗов «восьмого» семейства развал — 0°±30′, схождение — 0±1 мм. Так как передние колеса теперь тянут автомобиль, динамическая стабилизация при разгоне не требуется — колесо уже не катится позади ножки, а тянет ее за собой. Небольшой (1°30′) угол продольного наклона оси поворота сохранен для устойчивости при торможении. Значительный вклад в «правильное» поведение автомобиля вносит отрицательное плечо обката — при возрастании сопротивления качению колеса оно автоматически корректирует траекторию.
Углы для каждой модели автомобиля определяют после множества испытаний, доводочных работ и повторных испытаний. На старой, изношенной машине упругие деформации подвески (в первую очередь, резиновых элементов)
гораздо больше, чем у новой — колеса заметно расходятся от куда меньших сил. Но стоит остановиться, как в статике все углы вновь на своем месте. Так что регулировать разболтанную подвеску — пустой труд. Сначала
нужно ее отремонтировать.
Свести на нет все усилия разработчиков можно и другими способами.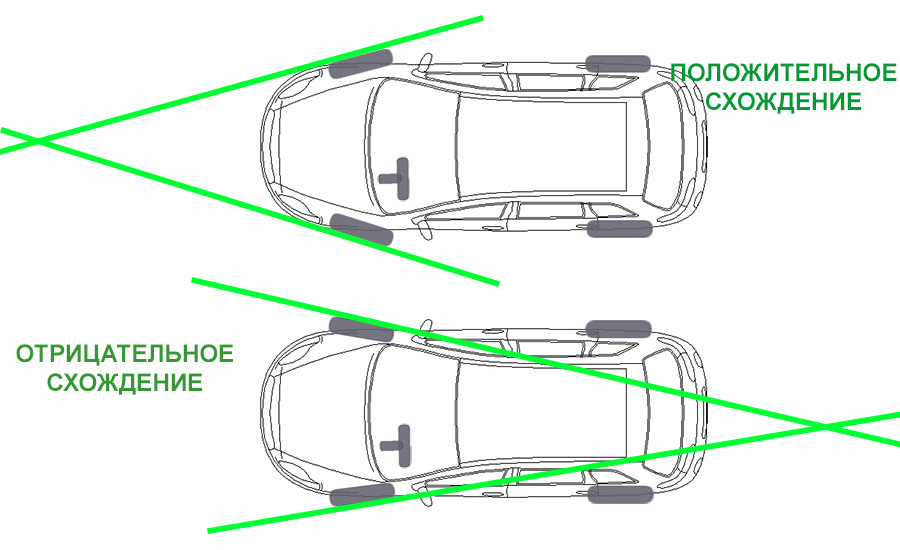 Например, хорошенько задрать заднюю часть автомобиля. Глядишь — кастер поменял знак и от динамической стабилизации остались воспоминания. И если при разгоне «спортсмен» еще сможет справиться с ситуацией, то при экстренном торможении — вряд ли. А если добавить нестандартные шины и колеса с иным вылетом, то просто невозможно предсказать, что получится в конечном итоге.
Например, хорошенько задрать заднюю часть автомобиля. Глядишь — кастер поменял знак и от динамической стабилизации остались воспоминания. И если при разгоне «спортсмен» еще сможет справиться с ситуацией, то при экстренном торможении — вряд ли. А если добавить нестандартные шины и колеса с иным вылетом, то просто невозможно предсказать, что получится в конечном итоге.
Теперь сходитесь — Авторевю
Все знают, как важно следить за углами установки передних колес: они влияют и на управляемость, и на износ шин… А как насчет задней оси? Что будет, если, к примеру, от удара о бордюр нарушится схождение задних колес?
Мы решили это проверить. Взяли седан Mazda 6, в задней многорычажной подвеске которого регулируется схождение, — и отправились на полигон.
Кстати, с «задним» схождением у нас уже был печальный опыт. Ровно год назад во время теста кроссоверов нас удивил Mitsubishi Outlander — он то и дело норовил сорваться в занос, чего за ним раньше не замечалось. Уже потом, после публикации, дилеры Mitsubishi выяснили причину: у той тестовой машины были немного нарушены углы установки задних колес. Вместо небольшого схождения колеса «расходились» — совсем чуть-чуть, на считанные доли градуса. Но этого оказалось достаточно для того, чтобы один из наших «обычных водителей», пытаясь проехать коридор «лосиного теста» на небольшой скорости в 65 км/ч, не удержал машину от разворота на 180
Ровно год назад во время теста кроссоверов нас удивил Mitsubishi Outlander — он то и дело норовил сорваться в занос, чего за ним раньше не замечалось. Уже потом, после публикации, дилеры Mitsubishi выяснили причину: у той тестовой машины были немного нарушены углы установки задних колес. Вместо небольшого схождения колеса «расходились» — совсем чуть-чуть, на считанные доли градуса. Но этого оказалось достаточно для того, чтобы один из наших «обычных водителей», пытаясь проехать коридор «лосиного теста» на небольшой скорости в 65 км/ч, не удержал машину от разворота на 180
На самом деле любой автомобиль очень чувствителен к изменению угла схождения задних колес. Представьте, что у машины отрицательное схождение — то есть задние колеса развернуты наружу по ходу движения. Тогда в повороте наружное заднее колесо (а при прочих равных условиях оно обладает гораздо большим сцеплением с покрытием, нежели внутреннее) будет слегка развернуто от центра поворота — и задняя ось будет стремиться обогнать переднюю. Автомобиль приобретает склонность к заносу!
Автомобиль приобретает склонность к заносу!
Заднее внешнее колесо, сильно повернутое наружу, уводит заднюю ось на обочину — машина срывается в занос
И наоборот, при положительном схождении (колеса смотрят «внутрь») нагруженное колесо направлено к центру поворота — оно работает на недостаточную поворачиваемость. Слегка сведенные к центру колеса увеличивают стабильность движения по скоростной прямой и помогают подвеске самой «подруливать» в нужную сторону, компенсируя порывы бокового ветра. Поэтому небольшое положительное схождение — хорошо! А вот отрицательное схождение («расхождение») — плохо.
Развернутое к центру поворота заднее «упорное» колесо перекладывает всю работу по восприятию боковой силы на переднюю ось — склонность к недостаточной поворачиваемости возрастает
Следите ли вы за углами установки задних колес? Возможно, они на вашей машине просто не регулируются — в зависимых задних подвесках (жесткие мосты у внедорожников) или полузависимых («скручивающаяся балка», как у вазовских переднеприводников) колеса установлены жестко.
Секреты подвескостроения У-У-К — журнал «АБС-авто»
Каждый раз, когда по тому или иному поводу речь заходит об углах установки колес, приходится слышать общепринятые фразы о том, что УУК призваны «компенсировать, снижать, повышать и улучшать». Обычно этим и ограничиваются. Если же предпринимаются попытки «копнуть глубже», а именно объяснить, почему колеса устанавливаются так, а не иначе, и каким образом достигается «снижение и повышение», чаще всего знания об этом предмете оказываются поверхностными, не совсем верными или неверными вовсе. Попробуем «повысить и улучшить» осведомленность в этой непростой, но очень интересной теме, заручившись поддержкой эксперта в области «подвескостроения» АЛЕКСАНДРА СОЛНЦЕВА, профессора, заместителя заведующего кафедрой «Автомобили» МАДИ (ГТУ). Как говорится, еще раз и поподробнее…
Обычно этим и ограничиваются. Если же предпринимаются попытки «копнуть глубже», а именно объяснить, почему колеса устанавливаются так, а не иначе, и каким образом достигается «снижение и повышение», чаще всего знания об этом предмете оказываются поверхностными, не совсем верными или неверными вовсе. Попробуем «повысить и улучшить» осведомленность в этой непростой, но очень интересной теме, заручившись поддержкой эксперта в области «подвескостроения» АЛЕКСАНДРА СОЛНЦЕВА, профессора, заместителя заведующего кафедрой «Автомобили» МАДИ (ГТУ). Как говорится, еще раз и поподробнее…
Экскурс в историю показывает, что мудреная установка колес применялась на различных средствах передвижения задолго до появления автомобиля. Вот несколько более или менее хорошо известных примеров.
Не секрет, что колеса некоторых карет и прочих колясок на конной тяге, предназначенных для «динамичной» езды, устанавливали с большим, хорошо заметным глазу положительным развалом. Делалось это для того, чтобы грязь, шматками летевшая с колес, не попадала в экипаж и на важных седоков, а разбрасывалась по сторонам.
У утилитарных повозок для неспешного передвижения все было с точностью до наоборот. Так, дореволюционные руководства о том, как построить хорошую телегу, рекомендовали ставить колеса с отрицательным развалом. В этом случае при потере нагеля, стопорящего колесо, оно не сразу соскакивало с оси. У возницы было время, чтобы заметить повреждение «ходовой», чреватой особенно большими неприятностями при наличии в телеге нескольких десятков пудов муки и отсутствии домкрата.
В конструкции орудийных лафетов (опять-таки наоборот) иногда применялся положительный развал колес. Понятно, что не с целью уберечь пушку от грязи. Так прислуге было удобно накатывать орудие за колеса руками сбоку, не опасаясь отдавить ноги. А вот у арбы ее огромные колеса, которые помогали запросто перебираться через арыки, были наклонены в другую сторону – к повозке. Достигавшееся при этом увеличение колеи способствовало повышению устойчивости среднеазиатского «мобиля», отличавшегося высоким расположением центра тяжести.
Какое отношение эти исторические факты имеют к установке колес современных автомобилей? Да, в общем, никакого. Тем не менее они позволяют сделать полезный вывод. Видно, что установка колес (в частности, их развал) не подчинена какой-либо единой закономерности. При выборе этого параметра «производитель» в каждом конкретном случае руководствовался разными соображениями, которые он считал приоритетными.
Итак, к чему стремятся конструкторы автомобильных подвесок при выборе УУК? Конечно, к идеалу. Идеалом для автомобиля, который движется прямолинейно, считается такое положение колес, когда плоскости их вращения (плоскости качения) перпендикулярны поверхности дороги, параллельны друг другу, оси симметрии кузова и совпадают с траекторией движения. В этом случае потери мощности на трение и износ протектора шин минимальны, а сцепление колес с дорогой, наоборот, максимально. Естественно, возникает вопрос: что же заставляет преднамеренно отклоняться от идеала? Забегая вперед, можно привести несколько соображений. Во-первых, мы судим об углах установки колес на основании статической картины, когда автомобиль неподвижен. Кто сказал, что в движении, при ускорении, торможении и маневрировании автомобиля она не меняется? Во-вторых, сокращение потерь и продление срока службы шин не всегда является приоритетной задачей.
Во-первых, мы судим об углах установки колес на основании статической картины, когда автомобиль неподвижен. Кто сказал, что в движении, при ускорении, торможении и маневрировании автомобиля она не меняется? Во-вторых, сокращение потерь и продление срока службы шин не всегда является приоритетной задачей.
Прежде чем рассказывать о том, какие факторы принимают в расчет разработчики подвесок, условимся, что из большого числа параметров, описывающих геометрию подвески автомобиля, мы ограничимся лишь теми, что входят в группу первичных (primary) или основных. Они называются так потому, что определяют настройку и свойства подвески, всегда контролируются при ее диагностике и регулируются, если таковая возможность предусмотрена. Это хорошо известные схождение, развал и углы наклона оси поворота управляемых колес. При рассмотрении этих важнейших параметров нам придется вспомнить и о других характеристиках подвески. Чтобы оживить память, можно воспользоваться приводящимися справками.
Схождение
В различных источниках, в том числе и серьезной технической литературе, часто приводится версия о том, что схождение колес необходимо для компенсации побочного действия развала. Мол, из-за деформации шины в пятне контакта «разваленное» колесо можно представить как основание конуса. Если колеса установлены с положительным углом развала (почему – пока неважно), они стремятся «раскатиться» в разные стороны. Чтобы этому противодействовать, плоскости вращения колес сводят. Версия, надо сказать, не лишена изящества, но не выдерживает критики. Хотя бы потому, что предполагает однозначную взаимосвязь между развалом и схождением. Следуя предлагаемой логике, колеса, имеющие отрицательный угол развала, обязательно должны устанавливаться с расхождением, а если угол развала нулевой, то и схождения быть не должно. В действительности это совсем не так. Действительность, как водится, подчиняется более сложным и неоднозначным закономерностям.
Мол, из-за деформации шины в пятне контакта «разваленное» колесо можно представить как основание конуса. Если колеса установлены с положительным углом развала (почему – пока неважно), они стремятся «раскатиться» в разные стороны. Чтобы этому противодействовать, плоскости вращения колес сводят. Версия, надо сказать, не лишена изящества, но не выдерживает критики. Хотя бы потому, что предполагает однозначную взаимосвязь между развалом и схождением. Следуя предлагаемой логике, колеса, имеющие отрицательный угол развала, обязательно должны устанавливаться с расхождением, а если угол развала нулевой, то и схождения быть не должно. В действительности это совсем не так. Действительность, как водится, подчиняется более сложным и неоднозначным закономерностям.
При качении наклоненного колеса в пятне контакта действительно присутствует боковая сила, которую часто так и называют – тяга развала. Она возникает в результате упругой деформации шины в поперечном направлении и действует в сторону наклона.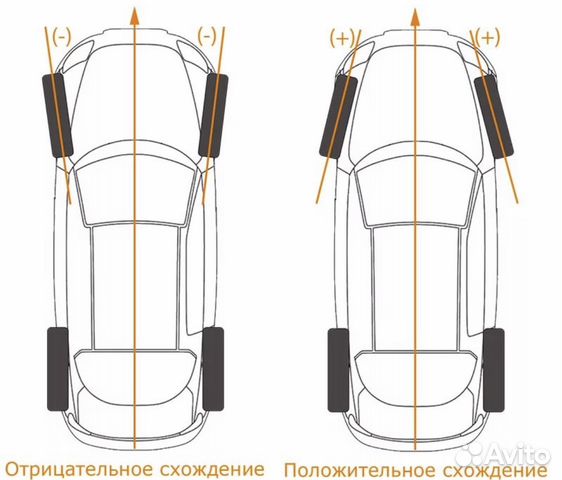 Чем больше угол наклона колеса, тем больше тяга развала. Именно ее используют водители двухколесной техники – мотоциклов и велосипедов – при прохождении поворотов. Им достаточно наклонить своего скакуна, чтобы заставить его «прописывать» криволинейную траекторию, которую остается лишь корректировать рулевым управлением. Тяга развала играет немаловажную роль и при маневрировании автомобилей, о чем будет сказано далее. Так что вряд ли ее стоит намеренно компенсировать схождением. Да и сам посыл, что из-за положительного угла развала колеса стремятся развернуться наружу, т. е. в сторону расхождения, неверен. Напротив, конструкция подвески управляемых колес в большинстве случаев такова, что при положительном развале его тяга стремится увеличить схождение. Так что «компенсация побочного действия развала» не при чем. Известно несколько факторов, обусловливающих необходимость схождения колес.
Чем больше угол наклона колеса, тем больше тяга развала. Именно ее используют водители двухколесной техники – мотоциклов и велосипедов – при прохождении поворотов. Им достаточно наклонить своего скакуна, чтобы заставить его «прописывать» криволинейную траекторию, которую остается лишь корректировать рулевым управлением. Тяга развала играет немаловажную роль и при маневрировании автомобилей, о чем будет сказано далее. Так что вряд ли ее стоит намеренно компенсировать схождением. Да и сам посыл, что из-за положительного угла развала колеса стремятся развернуться наружу, т. е. в сторону расхождения, неверен. Напротив, конструкция подвески управляемых колес в большинстве случаев такова, что при положительном развале его тяга стремится увеличить схождение. Так что «компенсация побочного действия развала» не при чем. Известно несколько факторов, обусловливающих необходимость схождения колес.
Первый состоит в том, что предварительно выставленным схождением компенсируется влияние продольных сил, действующих на колесо при движении автомобиля.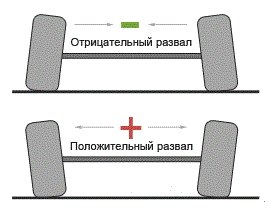 Характер и глубина (а значит, и результат) влияния зависят от многих обстоятельств: ведущее колесо или свободно катящееся, управляемое или нет, наконец, от кинематики и эластичности подвески. Так, на свободно катящееся колесо автомобиля в продольном направлении воздействует сила сопротивления качению. Она создает изгибающий момент, стремящийся развернуть колесо относительно узлов крепления подвески в направлении расхождения. Если подвеска автомобиля жесткая (например, неразрезная или торсионная балка), то эффект окажется не очень значительным. Тем не менее он обязательно будет, поскольку «абсолютная жесткость» – термин и явление сугубо теоретические. К тому же перемещение колеса определяется не только упругой деформацией элементов подвески, но и компенсацией конструктивных зазоров в их соединениях, колесных подшипниках и т. д. В случае подвески с большой податливостью (что характерно, например, для рычажных конструкций с эластичными втулками) результат многократно возрастет.
Характер и глубина (а значит, и результат) влияния зависят от многих обстоятельств: ведущее колесо или свободно катящееся, управляемое или нет, наконец, от кинематики и эластичности подвески. Так, на свободно катящееся колесо автомобиля в продольном направлении воздействует сила сопротивления качению. Она создает изгибающий момент, стремящийся развернуть колесо относительно узлов крепления подвески в направлении расхождения. Если подвеска автомобиля жесткая (например, неразрезная или торсионная балка), то эффект окажется не очень значительным. Тем не менее он обязательно будет, поскольку «абсолютная жесткость» – термин и явление сугубо теоретические. К тому же перемещение колеса определяется не только упругой деформацией элементов подвески, но и компенсацией конструктивных зазоров в их соединениях, колесных подшипниках и т. д. В случае подвески с большой податливостью (что характерно, например, для рычажных конструкций с эластичными втулками) результат многократно возрастет.
Если колесо не только свободно катящееся, но и управляемое, ситуация усложняется. За счет появления у колеса дополнительной степени свободы та же сила сопротивления оказывает двоякое воздействие. Момент, изгибающий переднюю подвеску, дополняется моментом, стремящимся развернуть колесо вокруг оси поворота. Разворачивающий момент, величина которого зависит от расположения оси поворота, воздействует на детали механизма рулевого управления и вследствие их податливости также вносит свою весомую лепту в изменение схождения колеса в движении. В зависимости от плеча обкатки вклад разворачивающего момента может быть со знаком «плюс» или «минус». То есть он может либо усиливать расхождение колес, либо противодействовать этому.
За счет появления у колеса дополнительной степени свободы та же сила сопротивления оказывает двоякое воздействие. Момент, изгибающий переднюю подвеску, дополняется моментом, стремящимся развернуть колесо вокруг оси поворота. Разворачивающий момент, величина которого зависит от расположения оси поворота, воздействует на детали механизма рулевого управления и вследствие их податливости также вносит свою весомую лепту в изменение схождения колеса в движении. В зависимости от плеча обкатки вклад разворачивающего момента может быть со знаком «плюс» или «минус». То есть он может либо усиливать расхождение колес, либо противодействовать этому.
Если не принять все это во внимание и установить изначально колеса с нулевым схождением, в движении они займут расходящееся положение. Из этого «вытекут» последствия, характерные для случаев нарушения регулировки схождения: повышенный расход топлива, пилообразный износ протектора и проблемы с управляемостью, о чем будет сказано далее. Сила сопротивления движению зависит от скорости автомобиля. Поэтому идеальным решением стало бы переменное схождение, обеспечивающее столь же идеальное положение колес на любых скоростях. Поскольку сделать это сложно, колесо предварительно «сводят» так, чтобы достичь минимального износа шин в режиме крейсерской скорости.
Поэтому идеальным решением стало бы переменное схождение, обеспечивающее столь же идеальное положение колес на любых скоростях. Поскольку сделать это сложно, колесо предварительно «сводят» так, чтобы достичь минимального износа шин в режиме крейсерской скорости.
Колесо, расположенное на ведущей оси, большую часть времени подвергается действию силы тяги. Она превышает силы сопротивления движению, поэтому равнодействующая сил будет направлена по ходу движения. Применив ту же логику, получим, что в этом случае колеса в статике нужно установить с расхождением. Аналогичный вывод можно сделать и в отношении управляемых ведущих колес.
Лучший критерий истины – практика. Если, памятуя об этом, посмотреть регулировочные данные для современных автомобилей, можно испытать разочарование, не обнаружив большой разницы в схождении управляемых колес задне- и переднеприводных моделей. В большинстве случаев и у тех и у других этот параметр будет положительным. Разве что среди переднеприводных автомобилей чаще встречаются случаи «нейтральной» регулировки схождения. Причина не в том, что описанная выше логика не верна. Просто при выборе величины схождения наряду с компенсацией продольных сил учитывают и другие соображения, которые вносят поправки в конечный результат. Одно из наиболее важных – обеспечение оптимальной управляемости автомобиля. С ростом скоростей движения и динамичности автотехники этот фактор приобретает все большее значение.
Причина не в том, что описанная выше логика не верна. Просто при выборе величины схождения наряду с компенсацией продольных сил учитывают и другие соображения, которые вносят поправки в конечный результат. Одно из наиболее важных – обеспечение оптимальной управляемости автомобиля. С ростом скоростей движения и динамичности автотехники этот фактор приобретает все большее значение.
Управляемость – понятие многогранное, поэтому стоит уточнить, что схождение колес наиболее ощутимо влияет на стабилизацию прямолинейной траектории автомобиля и его поведение на входе в поворот. Наглядно это влияние можно пояснить на примере управляемых колес. Допустим, в движении по прямой на одно из них оказывается случайное возмущающее воздействие от неровности дороги. Возросшая сила сопротивления поворачивает колесо в направлении уменьшения схождения. Через рулевой механизм воздействие передается на второе колесо, схождение которого, наоборот, увеличивается. Если изначально колеса имеют положительное схождение, сила сопротивления на первом уменьшается, а на втором – растет, что противодействует возмущению. Когда схождение равно нулю, противодействующий эффект отсутствует, а когда оно отрицательное – появляется дестабилизирующий момент, способствующий развитию возмущения. Автомобиль с такой регулировкой схождения будет рыскать по дороге, его придется постоянно ловить подруливанием, что недопустимо для обычного дорожного автомобиля. У этой «монеты» есть и обратная, позитивная сторона – отрицательное схождение позволяет добиться от рулевого управления наиболее быстрой реакции. Малейшее действие водителя тут же провоцирует резкое изменение траектории – автомобиль охотно маневрирует, легко «соглашается» на поворот. Такая регулировка схождения сплошь и рядом используется в автоспорте. Те, кто смотрят телепередачи о чемпионате WRC, наверняка обращали внимание на то, как активно приходится работать рулем тому же Лёбу или Гронхольму даже на относительно прямых участках трассы.
Через рулевой механизм воздействие передается на второе колесо, схождение которого, наоборот, увеличивается. Если изначально колеса имеют положительное схождение, сила сопротивления на первом уменьшается, а на втором – растет, что противодействует возмущению. Когда схождение равно нулю, противодействующий эффект отсутствует, а когда оно отрицательное – появляется дестабилизирующий момент, способствующий развитию возмущения. Автомобиль с такой регулировкой схождения будет рыскать по дороге, его придется постоянно ловить подруливанием, что недопустимо для обычного дорожного автомобиля. У этой «монеты» есть и обратная, позитивная сторона – отрицательное схождение позволяет добиться от рулевого управления наиболее быстрой реакции. Малейшее действие водителя тут же провоцирует резкое изменение траектории – автомобиль охотно маневрирует, легко «соглашается» на поворот. Такая регулировка схождения сплошь и рядом используется в автоспорте. Те, кто смотрят телепередачи о чемпионате WRC, наверняка обращали внимание на то, как активно приходится работать рулем тому же Лёбу или Гронхольму даже на относительно прямых участках трассы.
Аналогичное воздействие на поведение автомобиля оказывает схождение колес задней оси – уменьшение схождения вплоть до небольшого расхождения увеличивает «подвижность» оси. Этот эффект часто используют для компенсации недостаточной поворачиваемости автомобилей, например, переднеприводных моделей с перегруженной передней осью.
Таким образом, статические параметры схождения, которые приведены в регулировочных данных, представляют собой некую суперпозицию, а иногда и компромисс между желанием сэкономить на топливе и резине и добиться оптимальных для автомобиля характеристик управляемости. Причем заметно, что в последние годы превалирует последнее.
Развал
До недавнего времени наблюдалась тенденция именно разваливать колеса, т. е. придавать углам развала положительные значения. Многим наверняка памятны учебники по теории автомобиля, в которых установка колес с развалом объяснялась стремлением перераспределить нагрузку между внешним и внутренним ступичными подшипниками. Мол, при положительном угле развала большая ее часть приходится на внутренний подшипник, который проще выполнить более массивным и прочным. В результате выигрывает долговечность подшипникового узла. Тезис не очень убедительный, хотя бы потому, что он если и справедлив, то только для идеальной ситуации – прямолинейного движения автомобиля по абсолютно ровной дороге. Известно, что при маневрах и проезде неровностей, даже самых незначительных, подшипниковый узел испытывает динамические нагрузки, которые на порядок превышают статические силы. Да и распределяются они не совсем так, как «диктует» положительный развал колес.
Мол, при положительном угле развала большая ее часть приходится на внутренний подшипник, который проще выполнить более массивным и прочным. В результате выигрывает долговечность подшипникового узла. Тезис не очень убедительный, хотя бы потому, что он если и справедлив, то только для идеальной ситуации – прямолинейного движения автомобиля по абсолютно ровной дороге. Известно, что при маневрах и проезде неровностей, даже самых незначительных, подшипниковый узел испытывает динамические нагрузки, которые на порядок превышают статические силы. Да и распределяются они не совсем так, как «диктует» положительный развал колес.
Иногда пытаются толковать положительный развал как дополнительную меру, направленную на уменьшение плеча обкатки. Когда у нас дойдет дело до знакомства с этим важным параметром подвески управляемых колес, станет понятно, что такой способ воздействия далеко не самый удачный. Он сопряжен с одновременным изменением ширины колеи и включенного угла наклона оси поворота колеса, что чревато нежелательными последствиями. Существуют более прямые и менее болезненные варианты изменения плеча обкатки. К тому же его минимизация не всегда является целью разработчиков подвески.
Существуют более прямые и менее болезненные варианты изменения плеча обкатки. К тому же его минимизация не всегда является целью разработчиков подвески.
Более убедительно выглядит версия, что положительным развалом компенсируется смещение колес, происходящее при увеличении нагрузки на ось (в результате роста загрузки автомобиля или динамического перераспределения его массы при ускорении и торможении). Эластокинематические свойства большинства типов современных подвесок таковы, что с увеличением веса, приходящегося на колесо, угол развала уменьшается. Чтобы при этом обеспечить максимальное сцепление колес с дорогой, логично их предварительно чуть «развалить». Тем более что в умеренных дозах развал несильно отражается на сопротивлении качению и износе шин. Достоверно известно, что на выбор величины развала также оказывает влияние общепринятое профилирование дорожного полотна. В цивилизованных странах, где существуют дороги, а не направления, их поперечное сечение имеет выпуклый профиль. Чтобы в этом случае колесо оставалось перпендикулярным к опорной поверхности, ему нужно придать небольшой положительный угол развала.
Чтобы в этом случае колесо оставалось перпендикулярным к опорной поверхности, ему нужно придать небольшой положительный угол развала.
Просматривая спецификации на УУК, можно заметить, что в последние годы превалирует противоположная «развальная тенденция». Колеса большинства серийных автомобилей в статике устанавливаются с отрицательным развалом. Дело в том, что, как уже упоминалось, на первый план выходит задача обеспечения их наилучшей устойчивости и управляемости. Развал – это параметр, который оказывает определяющее влияние на так называемую боковую реакцию колес. Именно она противодействует центробежным силам, действующим на автомобиль в повороте, и способствует его удержанию на криволинейной траектории. Из общих соображений следует, что сцепление колеса с дорогой (боковая реакция) будет максимальным при наибольшей площади пятна контакта, т. е. при вертикальном положении колеса. На самом деле у колеса стандартной конструкции она достигает пика при небольших отрицательных углах наклона, что обусловлено вкладом упоминавшейся тяги развала. Значит, чтобы сделать колеса автомобиля предельно цепкими в повороте, нужно их не разваливать, а, наоборот, «сваливать». Этот эффект известен давно и столь же давно используется в автоспорте. Если предметно взглянуть на «формульный» болид, хорошо заметно, что его передние колеса установлены с большим отрицательным развалом.
Значит, чтобы сделать колеса автомобиля предельно цепкими в повороте, нужно их не разваливать, а, наоборот, «сваливать». Этот эффект известен давно и столь же давно используется в автоспорте. Если предметно взглянуть на «формульный» болид, хорошо заметно, что его передние колеса установлены с большим отрицательным развалом.
Что хорошо для гоночных болидов, не совсем подходит для серийных автомобилей. Чрезмерный отрицательный развал вызывает повышенный износ внутренней зоны протектора. С увеличением наклона колеса сокращается площадь пятна контакта. Сцепление колес при прямолинейном движении уменьшается, в свою очередь снижается эффективность ускорения и торможения. На способность автомобиля удерживать прямолинейную траекторию избыточный отрицательный развал влияет так же, как и недостаточное схождение, автомобиль становится излишне нервозным. Виновна в этом все та же тяга развала. В идеальной ситуации вызванные развалом боковые силы действуют на оба колеса оси и уравновешивают друг друга. Но стоит одному из колес потерять сцепление с дорогой, как тяга развала другого оказывается некомпенсированной и заставляет автомобиль отклониться от прямолинейной траектории. Кстати, если припомнить, что величина тяги зависит от наклона колеса, нетрудно объяснить боковой увод автомобиля при неодинаковых углах развала правого и левого колес. Одним словом, при выборе величины развала также приходится искать «золотую середину».
Но стоит одному из колес потерять сцепление с дорогой, как тяга развала другого оказывается некомпенсированной и заставляет автомобиль отклониться от прямолинейной траектории. Кстати, если припомнить, что величина тяги зависит от наклона колеса, нетрудно объяснить боковой увод автомобиля при неодинаковых углах развала правого и левого колес. Одним словом, при выборе величины развала также приходится искать «золотую середину».
Чтобы обеспечить автомобилю хорошую устойчивость, недостаточно в статике сделать углы развала отрицательными. Конструкторы подвески должны добиться, чтобы колеса сохраняли оптимальную (или близкую к ней) ориентацию на всех режимах движения. Выполнить это непросто, поскольку при маневрах любые изменения положения кузова, сопровождающиеся смещением элементов подвески (клевки, боковые крены и т. д.), приводят к существенному изменению развала колес. Как ни странно, эта задачка решается проще на спортивных автомобилях с их «зубодробительными» подвесками, отличающимися высокой угловой жесткостью и короткими ходами. Здесь статические величины развала (и схождения) меньше всего отличаются от того, как они выглядят в динамике.
Здесь статические величины развала (и схождения) меньше всего отличаются от того, как они выглядят в динамике.
Чем больше диапазон ходов подвески, тем больше изменение развала в движении. Поэтому тяжелее всего приходится разработчикам обычных дорожных автомобилей с максимально эластичными (для наилучшего комфорта) подвесками. Им приходится поломать голову над тем, как «совместить несовместимое» – комфорт и устойчивость. Обычно компромисс удается найти, «поколдовав» над кинематикой подвески. Существуют решения, позволяющие свести к минимуму изменение углов развала и придать этим изменениям желательный «тренд». Например, желательно, чтобы в повороте наиболее нагруженное внешнее колесо оставалось бы в том самом оптимальном положении – с небольшим отрицательным развалом. Для этого при крене кузова колесо должно еще больше «заваливаться» на него, что достигают оптимизацией геометрии направляющих элементов подвески. Помимо этого, стараются уменьшить сами крены кузова, применяя стабилизаторы поперечной устойчивости. Справедливости ради стоит сказать, что эластичность подвески не всегда враг устойчивости и управляемости. В «хороших руках» эластичность, напротив, способствует им. Например, при умелом использовании эффекта «самоподруливания» колес задней оси. Возвращаясь к теме разговора, можно резюмировать, что углы развала, которые указываются в спецификациях для легковых автомобилей, будут значительно отличаться от того, какими они окажутся в повороте.
Для этого при крене кузова колесо должно еще больше «заваливаться» на него, что достигают оптимизацией геометрии направляющих элементов подвески. Помимо этого, стараются уменьшить сами крены кузова, применяя стабилизаторы поперечной устойчивости. Справедливости ради стоит сказать, что эластичность подвески не всегда враг устойчивости и управляемости. В «хороших руках» эластичность, напротив, способствует им. Например, при умелом использовании эффекта «самоподруливания» колес задней оси. Возвращаясь к теме разговора, можно резюмировать, что углы развала, которые указываются в спецификациях для легковых автомобилей, будут значительно отличаться от того, какими они окажутся в повороте.
Завершая «разборку» со схождением и развалом, можно упомянуть еще об одном интересном аспекте, имеющем практическое значение. В регулировочных данных на УУК приводятся не абсолютные значения углов развала и схождения, а диапазоны допустимых величин. Допуски на схождение жестче и обычно не превышают ±10’, на развал – в несколько раз более свободные (в среднем ±30°). Это значит, что мастер, выполняющий регулировку УУК, может настроить подвеску, не выходя за пределы заводских спецификаций. Казалось бы, несколько десятков угловых минут – ерунда. Вогнал параметры в «зеленый коридор» – и порядок. Но давайте посмотрим, каков может быть результат. К примеру, в спецификациях для BMW 5-й серии в кузове Е 39 указываются: схождение 0°5’±10’, развал –0°13’±30’. Это значит, что, оставаясь в «зеленом коридоре», схождение может принять значение от –0°5’ до +15’, а развал от –43’ до +17’. То есть и схождение, и развал могут быть отрицательными, нейтральными или положительными. Имея представление о влиянии схождения и развала на поведение автомобиля, можно намеренно «подшаманить» эти параметры так, чтобы получить желаемый результат. Эффект не окажется разительным, но он обязательно будет.
Это значит, что мастер, выполняющий регулировку УУК, может настроить подвеску, не выходя за пределы заводских спецификаций. Казалось бы, несколько десятков угловых минут – ерунда. Вогнал параметры в «зеленый коридор» – и порядок. Но давайте посмотрим, каков может быть результат. К примеру, в спецификациях для BMW 5-й серии в кузове Е 39 указываются: схождение 0°5’±10’, развал –0°13’±30’. Это значит, что, оставаясь в «зеленом коридоре», схождение может принять значение от –0°5’ до +15’, а развал от –43’ до +17’. То есть и схождение, и развал могут быть отрицательными, нейтральными или положительными. Имея представление о влиянии схождения и развала на поведение автомобиля, можно намеренно «подшаманить» эти параметры так, чтобы получить желаемый результат. Эффект не окажется разительным, но он обязательно будет.
Продолжение следует
- Сергей Самохин
Развал, схождение и кастер — что это такое? – Автомастерская №1
Развал и схождение — параметры, отвечающие за управляемость автомобиля. Эту процедуру стоит проходить каждые 15-20 тыс. км., а также после ремонта подвески, рулевого управления, а также замены колес зима/лето. Иногда рекомендуется делать развал и схождения даже на новом автомобиле.
Эту процедуру стоит проходить каждые 15-20 тыс. км., а также после ремонта подвески, рулевого управления, а также замены колес зима/лето. Иногда рекомендуется делать развал и схождения даже на новом автомобиле.
Часто именно регулировка развала и схождения решают такие проблемы, как:
*быстрый износ покрышек
*биение руля
*когда авто тянет в сторону
Выполняются эта процедуры на специальном стенде, который позволяет выставлять значения с предельной точностью. В процессе, мастер обращает внимание на состояние колёса и подвески, т. к. в случае их износа не получится добиться хорошего результата.
Развал — это угол наклона колеса в вертикальной плоскости. Развал делится на положительный и отрицательный:
*Положительный — верхняя сторона колеса наклонена наружу.
*Отрицательный — верхняя сторона колеса наклонена внутрь.
От развала зависит сцепление колёс с дорогой.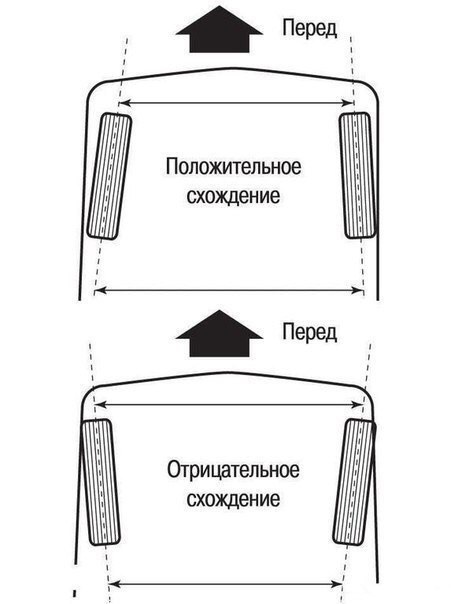 При отрицательном развале сцепление становится больше, т. к. увеличивается пятно контакта, но при этом резина снашивается быстрее.
При отрицательном развале сцепление становится больше, т. к. увеличивается пятно контакта, но при этом резина снашивается быстрее.
Схождение — угол плоскости колёс по отношению к направлению движения. Оно также бывает положительным и отрицательным
Положительное схождение — дальняя от водителя сторона колеса смотрит внутрь.
Отрицательное схождение — дальняя сторона смотрит наружу.
Если этот параметр будет выставлен неправильно, колёса также будут изнашиваться крайне быстро. Также, при неправильно схождении возникает биение руля, т. к. колеса сильнее передают все неровности. Этот параметр также может настраиваться на задних колёсах, в зависимости от конструкции авто.
Положительное схождение делает авто более стабильным при большой скорости, но при этом мы столкнемся с недостаточной поворачиваемостью. Отрицательное схождение повышает точность рулевого управления, но повышает износ резины.
Кастер — угол продольного наклона оси поворота авто. Благодаря этой регулировке автомобиль при выходе из поворота сам возвращает руль в в прямое положение.
Благодаря этой регулировке автомобиль при выходе из поворота сам возвращает руль в в прямое положение.
Чем меньше этот показатель, тем меньше радиус разворота авто, но при этом хуже управляемость на скорости. На спортивных авто, этот показатель наоборот делается больше — дабы повысить устойчивость и сделать управление более острым. Однако для повседневной езды такие настройки менее комфортные — руль становится тяжелым.
От каких факторов зависит выбор угла развала или схождения
Автор Дмитрий На чтение 2 мин. Просмотров 273 Опубликовано
Настройка подвески автомобиля выполняется с использованием современного оборудования, позволяющего установить углы наклона колесных дисков с точностью до десятых градуса. Таким образом, угол вертикального наклона (развал) и направления колеса по горизонтали (угол схождения) – выравнивают практически «в ноль». Такой подход обеспечивает наиболее равномерный износ протектора. Но, отрицательно сказывается на управляемости машины.
Такой подход обеспечивает наиболее равномерный износ протектора. Но, отрицательно сказывается на управляемости машины.
Общий совет по выбору угла схождения передней подвески – звучит следующим образом. На заднеприводном автомобиле, передние колеса разворачивают на 2-3 градуса друг к другу (создавая положительное схождение). Для переднего привода, наоборот, ведущие колеса устанавливают с отрицательным схождением.
На это есть свои причины. Передняя ось машины с задним приводом – испытывает воздействие сил, стремящихся развернуть диски наружу. Упругие элементы подвески должны им «противостоять». Чтобы получить нулевое схождение при движении с определенной скоростью, колеса изначально устанавливают с положительным схождением. А противоположное утверждение – будет верно для переднеприводных машин.
Развал – положительный, нулевой или отрицательный?
Заднюю подвеску легковых авто – в основном настраивают так, чтобы получить отрицательный развал. «Плюс» такого решения: улучшается управляемость машины в поворотах (при прохождении их на значительной скорости). Но есть и «минус»: преждевременно наступает износ покрышек. А именно, гораздо быстрее стирается внутренняя часть протектора.
«Плюс» такого решения: улучшается управляемость машины в поворотах (при прохождении их на значительной скорости). Но есть и «минус»: преждевременно наступает износ покрышек. А именно, гораздо быстрее стирается внутренняя часть протектора.
Как выбрать значение развала, чтобы получить оптимум? Это решит владелец автомобиля. Можно оставить значение «нулевым», и продлить жизнь покрышек. Правда, придется забыть о скоростном прохождении поворотов.
Присмотревшись к трековым легковым автомобилям или спорткарам, можно заметить, что диски задней оси – действительно, установлены с «ненулевым» развалом. Значение которого может достигать -5 градусов. Для гражданских версий, стандартный угол – от 0 до -1 градуса.
Небольшой положительный угол развала – изначально устанавливают с целью получить нулевое значение в дальнейшем.
Оцените статью: Поделитесь с друзьями!Что такое Развал колёс (положительный отрицательный, нулевой)
Передние колеса автомобиля устанавливаются так, что их верхние части наклонены наружу или вовнутрь (это можно отчетливо видеть, если смотреть на колеса спереди). Это называется «развалом” и измеряется в градусах наклона от вертикали. Когда вершина колеса наклонена наружу, это называется «положительным развалом». И наоборот, наклон вовнутрь называется «отрицательным развалом”.
Это называется «развалом” и измеряется в градусах наклона от вертикали. Когда вершина колеса наклонена наружу, это называется «положительным развалом». И наоборот, наклон вовнутрь называется «отрицательным развалом”.
НАЗНАЧЕНИЕ РАЗВАЛА
На автомобилях ранних выпусков колеса имели положительный развал для увеличения долговечности передней оси и для обеспечения контакта шины с поверхностью дороги под прямым углом, чтобы исключить неравномерный износ шин на дорогах, где середина дороги расположена выше, чем края.
На современных автомобилях подвеска и оси прочнее, чем на прежних и поверхность дороги более ровная, поэтому нет необходимости в положительном развале. Как результат, шины устанавливаются ближе к нулевому развалу (а некоторые автомобили имеют нулевой развал). Некоторые модели автомобилей имеют даже отрицательный развал для улучшения характеристик движения на поворотах.
ПОЛОЖИТЕЛЬНЫЙ РАЗВАЛ
Положительный развал
Назначениями положительного развала являются:
1. Уменьшение вертикальной нагрузки
Уменьшение вертикальной нагрузки
Если бы развал был нулевым, нагрузка на цапфу прилагалась бы в точке пересечения оси шины и цапфы, что обозначено F’ на рисунке ниже. Это способствовало бы изгибу цапфы колеса или поворотного кулака. Придавая колесу положительный развал, добиваются такого приложения нагрузки F, показанной на рисунке, к внутренней стороне цапфы, которое уменьшает усилие, действующее на цапфу и поворотный кулак.
2. Предотвращение соскальзывания колеса с цапфы
Реактивная сила F, которая по величине равна нагрузке на автомобиль, прилагается к колесу перпендикулярно дороге. F раскладывается на силу F,, перпендикулярную оси цапфы, и силу F2, параллельную оси цапфы. F2 воздействует на колесо в направлении вовнутрь, помогая предотвратить соскальзывание колеса с цапфы. Внутренний подшипник колеса имеет больший диаметр, чем наружный для восприятия этой нагрузки.
3. Исключение нежелательного отрицательного развала, вызываемого нагрузкой
Когда к автомобилю приложена нагрузка, вершины колес стремятся наклониться вовнутрь из-за деформации элементов подвески и втулок. Положительный развал также помогает предотвратить это явление.
Положительный развал также помогает предотвратить это явление.
4. Снижение усилия поворота
Это подробно рассмотрено в разделе о поперечном наклоне оси поворота
НУЛЕВОЙ РАЗВАЛ
Главной причиной применения нулевого развала является то, что он предотвращает неравномерный износ шин.
Если колеса имеют положительный развал, внешняя сторона шин движется по меньшему радиусу, чем внутренняя. Однако, поскольку скорость вращения шин одинакова с внешней и внутренней сторон, внешняя сторона шины должна проскальзывать по поверхности дороги, чтобы «сравняться» с внутренней стороной. Это вызывает ускоренный износ внешней стороны шины. В случае отрицательного развала имеет место противоположное явление, когда быстрее изнашивается внутренняя сторона шины.
ОТРИЦАТЕЛЬНЫЙ РАЗВАЛ
Отрицательный развалКогда к шине, имеющей развал, приложена вертикальная нагрузка, шина будет стремиться сдвинуться вниз. Однако, поскольку она упирается в поверхность дороги, протектор будет деформироваться, как показано на рисунке ниже. В то же время, упругость шины препятствует этой деформации и, следовательно, действует на поверхность дороги в направлении (А). В результате реакции в направлении А шина кренится в направлении В. Сила, действующая в направлении (В), называется «осевым усилием, зависящим от развала”. Осевое усилие, зависящее от развала, возрастает с увеличением наклона шины относительно поверхности дороги (развал относительно дороги), а также с увеличением нагрузки.
В то же время, упругость шины препятствует этой деформации и, следовательно, действует на поверхность дороги в направлении (А). В результате реакции в направлении А шина кренится в направлении В. Сила, действующая в направлении (В), называется «осевым усилием, зависящим от развала”. Осевое усилие, зависящее от развала, возрастает с увеличением наклона шины относительно поверхности дороги (развал относительно дороги), а также с увеличением нагрузки.
При повороте автомобиля осевое усилие на внешних шинах, зависящее от развала, действует так, чтобы уменьшить усилие поворота, обусловленное увеличением положительного развала. Центробежная сила, взаимодействуя с пружинами подвески, наклоняет поворачивающий автомобиль, изменяя при этом развал. На некоторых моделях автомобилей используются преимущества этого эффекта и вводится незначительный отрицательный развал при прямолинейном движении с тем, чтобы уменьшить положительный развал при повороте, снижая осевое усилие, зависящее от развала, и обеспечивая достаточное усилие поворота.
[Предыдущая глава] [Следующая глава] | ||||||||||||||||||
Глава 22 Ключевые слова: Графический анализ, линия спроса-1: 1, фория расстояния, относительная и фузионная вергенция, ZCVSBV, шпора Альперна, критерий Ширда, критерий Персиваля Наброски Часть V: Клиническое представление компонентов Мэддокса
| ||||||||||||||||||
| ||||||||||||||||||
Диагональная линия обозначается несколькими терминами, включая линию спроса, линию Дондера и линию 1: 1.Оптометрические данные, полученные с целью на разных расстояниях обзора, отображаются в соответствии с линиями спроса. Например, фория расстояния отображается символом (x) слева для exo и справа для eso от линии спроса, когда она пересекает нижнюю часть графика. Обратное значение наклона линии фории является прямой мерой рассчитанного отношения AC / A. Результаты размытия, разрыва и восстановления положительной и отрицательной относительной конвергенции отображаются справа и слева от линии спроса соответственно на соответствующих уровнях стимула аккомодации. Разделение между точками размытия для положительной и отрицательной относительной конвергенции называется шириной зоны четкого одиночного бинокулярного зрения.Прямые линии соответствуют ближним и дальним измерениям точек размытия до базовой призмы и призмы вне базы. Линии обычно почти параллельны линии фории и образуют боковые границы зоны четкого единственного бинокулярного зрения (ZCSBV). Сверху зона ограничена монокулярной амплитудой аккомодации. Область внутри этого параллелограмма, образованная пределами основания и основания, определяет все возможные комбинации стимулов конвергенции и аккомодации, на которые может реагировать бинокулярная зрительная система.Преимущества этого метода представления клинических данных:
Несколько форм графического анализа показаны ниже. Такие формы можно использовать для записи клинических оптометрических данных. Пример заполненного графика типичных результатов испытаний показан на рис. 22.3. | ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
Положительная конвергенция слияния (PFC) = Положительная относительная конвергенция (PRC) — Phoria (где eso равно +) Относительная вергенция — это термин, используемый для описания амплитуды вергенции, измеренной клинически.Эти данные нанесены на график по обе стороны от линии спроса. Положение линии спроса в пределах диапазона относительной вергенции используется как индикатор для предписывающей призмы. | ||||||||||||||||||
| ||||||||||||||||||
Критерий Персиваля гласит, что рецепт должен быть равен следующему: | ||||||||||||||||||
| ||||||||||||||||||
Критерий Шеарда гласит, что рецепт должен быть равен следующему: Аномально узкие зоны четкого единственного бинокулярного зрения являются симптомами бинокулярный сенсорный дефицит, который часто можно исправить с помощью ортопедии. | ||||||||||||||||||
[Предыдущая глава] [Следующая глава] | ||||||||||||||||||
1
Теперь мы рассмотрим применение различных тестов сходимости / расхождения, которые мы рассмотрели до сих пор, к некоторым рядам, не уточняя, какой тест применять конкретно. {\ infty} \ frac {1} {1 + \ sqrt {n}} $ расходится.
{\ infty} \ frac {1} {1 + \ sqrt {n}} $ расходится.
Сходимость и расходимость несобственных интегралов
Сходимость и расходимость несобственных интеграловСходимость и расходимость несобственных интегралов
Рассмотрим функцию f ( x ), которая демонстрирует поведение типа I или типа II. на интервале [ a , b ] (другими словами, интеграл неправильный). Ранее мы видели, что этот интеграл определяется как предел.Поэтому у нас есть два случая:
- 1
- предел существует (и является числом), в этом случае мы говорим, что несобственный интеграл — сходящийся ;
- 2
- предел не существует или он бесконечен, тогда мы говорим что несобственный интеграл равен расходящемуся .
Если несобственный интеграл разбить на
сумма несобственных интегралов (поскольку f ( x ) представляет более одного
неправильное поведение на [ a , b ]), то интеграл сходится тогда и только тогда
если любой единственный несобственный интеграл сходится.
Пример. Рассмотрим функцию на [0,1]. У нас есть
Следовательно, несобственный интеграл
сходится тогда и только тогда, когда несобственные интегралы
сходятся. Другими словами, если один из этих интегралов равен
расходится, интеграл
будет расходиться.
P-интегралы Рассмотрим функцию (где p > 0) для. Смотря на эта функция внимательно мы видим, что f ( x ) представляет неправильное поведение при 0 и только.Чтобы обсудить сближение или расхождение
нам нужно изучить два несобственных интеграла
У нас есть
а также
Для обоих пределов нам нужно вычислить неопределенный интеграл
У нас есть два случая:
- если p = 1, то имеем
- если, то имеем
Чтобы принять решение о схождении или расхождении двух вышеуказанных
несобственные интегралы, нам необходимо рассмотреть случаи: p <1, p = 1 и p > 1.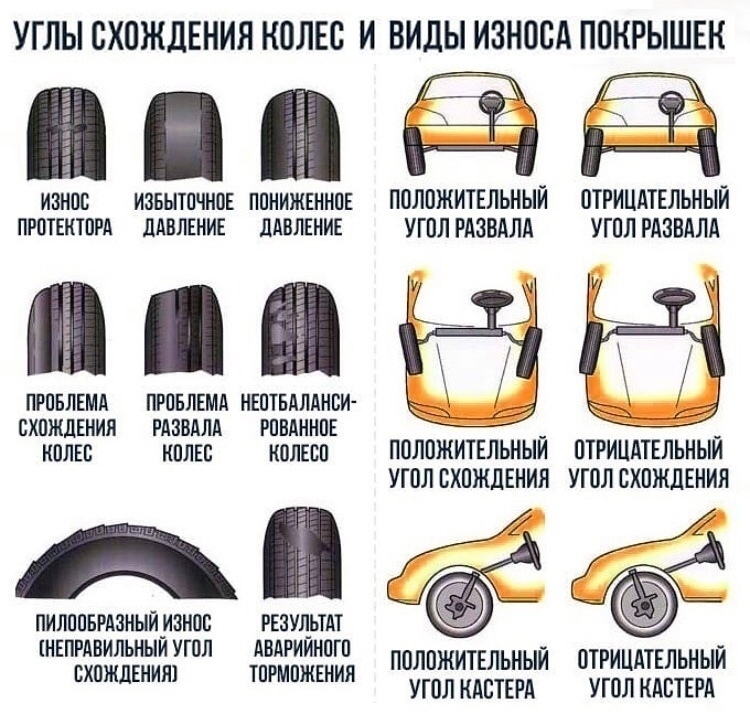
- Если p <1, то имеем
а также
- Если p = 1, то имеем
а также
- Если p > 1, имеем
а также
P-Test: Независимо от значения числа p , несобственный интеграл
всегда расходится.Кроме того, у нас есть
- это сходится тогда и только тогда, когда p <1
- это сходится тогда и только тогда, когда p > 1
На следующих страницах мы увидим, как несколько простых тестов помогут в решая, сходится или расходится несобственный интеграл.
[Геометрия] [Алгебра] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра] [Тригонометрия] С.Домашняя страница O.S MATHematicsВам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Mohamed A. KhamsiВт, 3 декабря 17:39:00 MST 1996 Авторское право 1999-2020 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час
| Трансляция |
| Disney тестирует новую функцию «Групповые просмотры» для Disney Plus |
| Disney постепенно внедряет новую функцию «Group Watch» для пользователей Disney Plus, которая позволяет пользователям смотреть контент вместе.Скриншоты новой функции опубликованы на Disney … еще |
| Юридические и Патенты |
| Налоги Google, Facebook как телекоммуникационные компании? Испания рассматривает новый закон |
| Согласно предложенным правилам интернет-компании, такие как Alphabet Inc.и Facebook Inc, должны будут раскрыть свои продажи через службы обмена сообщениями в стране. … еще |
| Отчеты |
| U.Сельским телекоммуникационным сетям требуется 1,8 миллиарда долларов для демонтажа оборудования Huawei и ZTE — FCC |
| Сельские телекоммуникационные сети США, которые полагались на недорогое сетевое оборудование от китайских компаний Huawei Technologies Co [HWT.UL] и ZTE Corp, заявили правительству, что их замена обойдется в 1,837 миллиарда долларов. … еще |
| Политика и регулирование |
| Приговор СМА приносит уверенность; Теперь DoT должен сосредоточиться на простоте бизнеса: BIF |
| Вердикт AGR позволит компаниям уверенно продвигать свои бизнес-планы, и теперь DoT должен сосредоточиться на шагах, которые сделают телекоммуникационный сектор прибыльным и …более |
| Телеком |
| Moody’s изменяет прогноз рейтингов Airtel с «негативного» на «стабильный» |
| Moody’s Investor Service подтвердило корпоративный семейный рейтинг Bharti Airtel Ba1 (CFR) и изменило прогноз на «стабильный» с «негативного» после прояснения сроков выплаты скорректированной валовой выручки (AGR). …более |
Сходимость биномиального, пуассоновского, отрицательно-биномиального и гамма-распределения к нормальному распределению: метод функций, генерирующих момент
Субхаш К.Багуи 1 , К. Л. Мехра 2
1 Департамент математики и статистики, Университет Западной Флориды, Пенсакола, США
2 Департамент математических и статистических наук, Университет Альберты, Эдмонтон, США
Для корреспонденции: Субхаш К. Багуи, Департамент математики и статистики, Университет Западной Флориды, Пенсакола, США.
| Электронная почта: |
Авторские права © 2016 Научно-академическое издательство. Все права защищены.
Это произведение находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Абстрактные
В этой статье мы используем моментные производящие функции (MGF) биномиального, пуассоновского, отрицательно-биномиального и гамма-распределений, чтобы продемонстрировать их сходимость к нормальности, когда один из их параметров неограниченно увеличивается.Мотивация этой работы состоит в том, чтобы подчеркнуть прямое использование MGF в доказательствах сходимости. Эти конкретные доказательства MGF не могут быть все вместе в книге или одной статье. Читатели сочтут эту статью очень информативной и особенно полезной с педагогической точки зрения.
Ключевые слова: Биномиальное распределение, Центральная предельная теорема, Гамма-распределение, Производящая функция момента, Отрицательно-биномиальное распределение, Распределение Пуассона
Цитируйте эту статью: Subhash C.Багуи, К. Л. Мехра, Сходимость биномиального, пуассоновского, отрицательно-биномиального и гамма-распределения к нормальному распределению: метод функций, генерирующих момент, Американский журнал математики и статистики , Vol. 6 No. 3, 2016, pp. 115-121. DOI: 10.5923 / j.ajms.20160603.05.
1. Введение
- Основная центральная предельная теорема (CLT) говорит нам, что при надлежащей нормализации суммы независимых одинаково распределенных (т.i.d.) случайные величины (с.в.) из любого распределения с конечным средним и дисперсией будут иметь свои распределения, сходящиеся к нормальному, поскольку размер выборки n стремится к бесконечности. Если мы принимаем эту CLT и знаем, что биномиальные, пуассоновские, отрицательно-биномиальные и гамма-значения сами по себе являются суммами i.i.d. r.v.’s, мы можем сделать вывод о предельной нормальности этих распределений, применяя этот CLT. Однако мы должны отметить, что доказательство этого CLT основано на использовании теории характеристических функций, включающей комплексный анализ, изучением которой в основном занимаются только высшие математические дисциплины в колледжах и университетах.Действительно, существуют другие методы доказательства в конкретных случаях, например, в случае биномиального и пуассоновского распределений посредством аппроксимации функций массы вероятности (pmf) соответствующей нормальной функцией плотности вероятности (pdf) с использованием формулы Стирлинга (см. Stigler , SM 1986, pp.70-88, [8]; Bagui et al. 2013b, p. 115, [2]), или просто аппроксимируя отношения последовательных членов pmf распределения, с которым мы имеем дело (см. Proschan , МА 2013, стр. 62-63, [6]). Однако, используя методологию параллельных (к характеристическим функциям) MGF, которая не предполагает комплексного анализа, мы можем относительно легко достичь той же цели.Это то, что мы предлагаем явно продемонстрировать в данной статье. Структура статьи следующая. В разделе 2 мы приводим некоторые полезные предварительные результаты. Эти результаты будут использованы в разделе 3. В разделе 3 мы приводим все детали сходимости всех упомянутых выше распределений к нормальному распределению. Раздел 4 содержит несколько заключительных замечаний.
2. Предварительные сведения
- В этом разделе мы сформулируем некоторые результаты, которые будут использоваться в различных доказательствах, представленных в разделе 3. Определение 2.1 . Пусть будет r.v. с функцией массы вероятности (pmf) или функцией плотности вероятности (pdf) Тогда производящая функция момента (mgf) с.в. определяется как предполагается существовать и быть конечным для всех для Если имеет нормальное распределение со средним значением и дисперсией, тогда mgf of определяется [3].Если, то говорят, что имеет стандартное нормальное распределение (т. Е. Нормальное распределение с нулевым средним и единицей дисперсии). MGF задается как Позвольте обозначить кумулятивную функцию распределения (cdf) с.в. Теорема 2.1 . Пусть и будут двумя кумулятивными функциями распределения (cdf), моменты которых существуют. Если MGF существуют для с.в. и и для всех в , то для всех (т.е.е., для всех Распределение вероятностей не всегда определяется своими моментами. Допустим, есть cdf и моменты, которые существуют для всех. Если имеет положительный радиус сходимости для всех (Billingsley 1995, Section 30, [4]; Serfling 1980, p. 46, [7]), то mgf существует в интервале и, следовательно, однозначно определяет распределение вероятностей. Более слабое достаточное условие для последовательности моментов для однозначного определения распределения вероятностей: Это достаточное условие принадлежит Карлеману (Chung 1974, p.82, [5]; Серфлинг 1980, стр. 46, [7]). Теорема 2.2 . Пусть будет последовательностью с.в. с соответствующей последовательностью MGF e как и будет с.в. с mgf , которые, как предполагается, существуют для всех Если для , то Обозначение означает, что, поскольку распределение r.v. сходится к распределению r.v. Лемма 2.1 . Пусть будет последовательностью действительных чисел. Тогда при условии, что и не зависят от и CLT ( См. Bagui et al. 2013a, [1]) . Пусть будет последовательностью независимых и одинаково распределенных (i.i.d.) случайных величин со средним значением , и дисперсией , и набором и . Затем , как , где обозначает нормальное распределение со средним значением 0 и дисперсией 1 . По поводу определения 2.1, теоремы 2.1, теоремы 2.2 и леммы 2.1 см. Casella and Berger, 2002, стр. 62-66, [4] и Bain, Engelhardt, 1992, p. 234, [3].
3. Конвергенция Mgf’s
3.1. Биномиальные вероятности
- Биномиальные вероятности применяются к ситуациям, включающим серию независимых и идентичных испытаний с двумя возможными исходами — успех с вероятностью и неудача с вероятностью — в каждом испытании.Пусть будет количество успехов в испытаниях, тогда имеет биномиальное распределение с параметрами и. Функция массы вероятности задается как Таким образом, среднее значение is и дисперсия is. Mgf задается как Let. Используя упрощенные обозначения, мы имеем. Ниже мы выводим MGF. Теперь MGF задается как
| (3.1) |
| (3.2) |
| (3.3) |
| (3.4) |
3.2. Пуассон
- Распределение Пуассона подходит для прогнозирования редких событий в течение определенного периода времени. Позвольте быть пуассоновской с.в. с параметром Функция массы вероятности задается как Среднее значение, так и дисперсия: МГФ задается по формуле Для удобства обозначений позвольте и Ниже мы выводим МГФ, которая равна
| (3.5) |
3.3. Отрицательный бином
- Рассмотрим бесконечную серию независимых испытаний, каждое из которых имеет два возможных исхода: успех или неудачу. Позвольте и Определите случайную переменную как количество неудач до успеха. Тогда имеет отрицательное биномиальное распределение с параметрами и. Таким образом, функция массы вероятности задается как Среднее значение равно, а дисперсия определяется как МГФ может быть получена как Пусть Теперь МГФ задается по формуле
| (3.6) |
| (3,7) |
| ( 3.8) |
| (3.9) |
3.4. Гамма
- Гамма-распределение подходит для моделирования времени ожидания событий.Позвольте быть гамма r.v. с pdf и The называется параметром формы распределения и масштабным параметром распределения. Для удобства обозначим как. Хорошо известно, что среднее значение is и дисперсия is. Mgf задается как Пусть mgf задается как
| (3.10) |
4. Заключительные замечания
- Хорошо известно, что биномиальная с.в. это сумма i.мне бы. Bernouli r.v.’s, с.в. Пуассона, с положительным целым числом, сумма i.i.d. р. v.’s, отрицательно-биномиальная r.v. сумма i.i.d. геометрические с.в. и гамма-с.в. сумма i.i.d. экспоненциальная с.в. Принимая во внимание эти факты, можно легко сделать вывод, применяя вышеупомянутый общий CLT, что вышеупомянутые распределения после надлежащей нормализации сходятся к нормальному распределению, поскольку количество членов в их соответствующих суммах увеличивается до бесконечности. Но эти факты могут быть недоступны для студентов бакалавриата, особенно тех, кто не изучает математику.Однако, как было продемонстрировано в предыдущем разделе 3 для биномиального, пуассоновского, отрицательно-биномиального и гамма-распределений, при решении проблем сходимости распределений, когда отдельные MGF существуют и доступны, мы можем эффективно использовать технику MGF для формального вывода их предельных распределений. На наш взгляд, последний метод естественен, столь же поучителен и более управляем. В любом случае это альтернативный подход. При доказательстве общей центральной предельной теоремы с использованием MGF и Бейн, и Энгельхардт (1992), [3] и Inlow (2010), [6a] используют MGF суммы i.i.d r.v’s. Но мы используем существующие MGF всех вышеупомянутых распределений, не рассматривая их как суммы i.i.d. r.v.’s. Бейн и Энгельхардт (1992), [3] обсуждают доказательство сходимости бинома к нормальному с помощью mgf. Но эта статья формализует MGF-доказательства набора распределений. Бумага, оформленная таким образом, может служить отличным учебным пособием. Доказательства просты и требуют только дополнительных знаний о разложении в ряд Тейлора, помимо навыков работы с алгебраическими уравнениями и основными вероятностными концепциями.Материал должен представлять педагогический интерес, и его можно обсуждать на занятиях, где только базовые знания и навыки работы с алгебраическими выражениями являются единственными базовыми требованиями. Статья также должна представлять интерес для студентов старших курсов по теории вероятностей и статистики.
БЛАГОДАРНОСТИ
- Авторы благодарны главному редактору и анонимному рецензенту за внимательное прочтение статьи.
Каталожные номера
| [1] | Багуи, С.К., Бхаумик, Д.К., Мехра, К.Л. (2013a). Несколько контрпримеров, полезных при обучении центральной предельной теореме, The American Statistician , 67 (1), 49-56. |
| [2] | Багуи, С.С., Багуи, С.С., Хемасинья, Р. (2013b). Формула Стирлинга нестрогого доказательства, Mathematics and Computer Education , 47 (2), 115-125. |
| [3] | Бейн, Л.Дж. и Энгельхардт, М. ((1992). Введение в вероятностную и математическую статистику , 2 nd edition, Belmont: Duxbury Press. |
| [4] | Биллингсли П. (1995). Probability and Measure , 3 rd edition, New York: Wiley. |
| [5] | Casella, G. and Berger, R.L. (2002). Статистический вывод , Pacific Grove: Duxbury. |
| [6] | Chung, K.L (1974). Курс теории вероятностей , Нью-Йорк: Academic Press. а. Inlow, Марк (2010). Доказательство функции производства моментов центральной предельной теоремы Линдеберга-Леви, The American Statistician , 64 (3), 228-230. |
| [7] | Proschan, M.A. (2008). Нормальное приближение к биному, The American Statistician, 62 (1), 62-63. |
| [8] | Serfling, R.J. (1980). Аппроксимационные теоремы математической статистики , Нью-Йорк; Вайли. |
| [9] | Stigler, S.M. (1986), История статистики: Измерение неопределенности до 1900 года , Кембридж, Массачусетс: Издательство Belknap Press of Harvard University Press. |
Аномалии сходимости
Аномалии сходимости________________________________________________________________
Контурные записки для сопровождения Городского университета 2 лекция по курсу клинической практики года
Д-р Саймон Барнард PhD BSc FCOptom FAAO DCLP
Студентам рекомендуется пройти курс Evans BJW (1997 ) Pickwells Binocular Vision Anomalies.Исследование и лечение. 3 rd Edition, Butterworth-Heinemann, Oxford .
Оценка сходимости
Ближайшая точка схождения
Ближнюю точку конвергенции (NPC) глаз можно исследовать, поместив фиксирующий объект на расстоянии 30-40 см в средней плоскости головы пациента. Пациента попросили сохранять фиксацию на объекте, пока он приближается к пациенту, пока один из глаз не потеряет фиксацию и не отделится от другого глаза (von Noorden, 1990).Это также называется тестом отжимания и проверяет комбинацию рефлекторной и произвольной конвергенции (Mallett, 1988). Его также называют тонической конвергенцией (Даум, 1983b). Согласно фон Нордену (1990), нормальный NPC должен быть 8-10 см, причем все, что более удалено от него, является дефектным или удаленным. Тест отжимания также может быть проведен субъективно, когда практикующий попросит пациента сообщить, когда цель впервые видна при диплопии.Целью должна быть жирная вертикальная линия (Mallett, 1988).
Прыжок схождения
Конвергенция прыжка (фазовая или ступенчатая) проверяется, когда пациента просят изменить фиксацию с удаленной цели на ближнюю, расположенную в средней плоскости на расстоянии 15 см от головы пациента. Положение ближней цели можно изменять, чтобы определить ближайшую точку (Rashbass & Westheimer, 1961; Pickwell & Stevens, 1975). Этот тест носит почти полностью добровольный характер.Практикующий может наблюдать либо плавное схождение обоих глаз на расстоянии, либо множество аномальных реакций, включая медленное или неуверенное движение; чрезмерная конвергенция; версионные движения, за которыми следует конвергенция; либо нет движения ни одного глаза, либо движения только одного глаза (Pickwell & Hampshire, 1981).
Рефлекторное схождение
Хотя невозможно полностью изолировать рефлекторную конвергенцию , тест Капобианко, в котором используется темно-красный фильтр, помещенный перед одним глазом для частичной диссоциации, предназначен для измерения рефлекторной конвергенции с незначительным произвольным вводом или без него (Капобианко , 1952).
Аномалии вергентности
Существует несколько способов классификации аномалий вергенции (von Noorden, 1990; Evans, 1997). Полезный, но упрощенный метод — классифицировать аномалии в соответствии с расстоянием фиксации, на котором они проявляются. Самым ранним описанием этого типа является классификация сбоев дивергенции и конвергенции Дуэйна-Уайта (Borisch, 1970). Эта классификация применяется к косоглазию , а не к гетерофории, и поэтому, когда используется в контексте гетерофории, как правило, подразумевает, что гетерофория является формой скрытого косоглазия.Tait (1951) модифицировал исходную классификацию, чтобы включить в нее концепцию вовлечения аккомодационной конвергенции, и его концепции будут включены в обсуждение, которое будет продолжено ниже.
Недостаточность дивергенции
Недостаточность дивергенции (DI) описывает состояние, при котором у пациента наблюдается декомпенсированная эзофория для зрения вдаль с отсутствием или меньшей амплитудой хорошо компенсированной эзофории вблизи (Evans, 1997). Tait (1951) далее классифицировал DI как первичный или вторичный, , и их характеристики описаны в таблице 1 . Оба типа могут быть связаны с избытком сходимости.
| Первичный DI | Вторичный DI | |
| Дистанционная эзофория | до 8D | > 8D |
| Рядом с эзофорией | присутствует | большая амплитуда |
| Соотношение AC / A | нормальный | сверх |
Таблица 1 Категории недостаточности дивергенции (Tait, 1951).
Превышение расхождения
Термин d превышение схождения ( DE) описывает декомпенсированную экзофорию для расстояния, при которой любая экзофория вблизи имеет меньшую амплитуду и хорошо компенсируется (Evans, 1997). Tait (1951) описал это как выраженную экзофорию вдали с такой же или меньшей экзофорией вблизи. Если NPC нормальный, он может быть описан как первичный DE, а если нет, он может быть описан как вторичный DE.
Превышение схождения
Избыток конвергенции ( CE) описывает декомпенсированную эзофорию вблизи с любой эзофорией для расстояния, имеющей меньшую амплитуду и хорошо компенсируемую (Evans, 1997). Tait (1951) определяет CE аналогично: ортофория или умеренная эзофория для расстояния и более выраженная эзофория для близкого расстояния, причем причиной является чрезмерное соотношение ACA.
Распространенной причиной CE является высокое соотношение AC / A и / или нескорректированная гиперметропия e.г., классическое косоглазие типа Дондерса. Другая причина может иметь психосоматическую природу.
Симптомы могут быть особенно связаны с тесной работой и могут включать лобную головную боль, утомляемость глаз, нечеткость зрения, инерцию аккомодации (см. Примечания по аномалиям аккомодации).
Обследование может включать циклоплегическую рефракцию, определение соотношения АС / А
Спазм конвергенции
Это очень редко и может быть связано с цилиарным спазмом.Может быть вызвано психосоматическим действием. Сообщите о любых новых случаях.
Паралич конвергенции
Конвергенция не может быть обнаружена даже с помощью призмы. Причины включают аномалии 3 rd N, травму головы, синдром Паринауда (паралич конвергенции + паралич вертикального взора).
Все новые случаи требуют направления на нейроофтальмологическое заключение.
Недостаточность схождения
Недостаточность конвергенции (CI) — это состояние, при котором пациент не может поддерживать достаточную конвергенцию для комфортного зрения вблизи (Evans, 1997).Несмотря на это простое определение, КИ, вероятно, правильнее назвать синдромом. Хотя CI часто ассоциируется с экзофорией слабости конвергенции , , который представляет собой декомпенсированную экзофорию для ближнего, при этом экзофория на любом расстоянии одновременно хорошо компенсируется и имеет меньшую амплитуду, чем для ближнего (Evans, 1997). , , фон Ноорден (1990) указал. что КИ может произойти при наличии эзофории вблизи.
Хотя вышеперечисленные категории могут быть полезны для описательных целей, на практике клинические признаки не всегда четкие, и Evans (1997) также определяет базовую (или смешанную) эзофорию и экзофорию , в которых амплитуда гетерофории не отличается от расстояние до ближайшего.
CI — одна из наиболее частых причин дискомфорта в глазах. Фон Норден (1990) предположил, что это самая частая причина мышечной астенопии и что она часто имеет этиологическую связь с трудностями аккомодации.
von Graefe (1855) (цитируется von Noorden, 1990) описал симптомы, возникающие при КИ. Упоминания о КИ также можно найти в учебниках, опубликованных на рубеже 18–– гг. (Берри, 1893; Кларк, 1893).Впоследствии Дуэйн (1897) дал клиническое описание КИ.
Описание Рауса и др. (1998) развило описание Дуэйна (1897) и Тейта (1951). Пока есть либо ортофория, либо небольшое (~ 2–4 D ) экзофория, нормальные версии, часто субнормальное отведение (~ 8-10 дней и не более ~ 15D ), а сходимость, вызванная призмой, часто уменьшалась до ~ 14–20 дней или менее. Для зрения вблизи существует выраженная экзофория 12D. или выше, обычные версии и NPC 7.5 см или больше.
Daum (1986a), используя критерий большего экзо-отклонения для близости по сравнению с расстоянием, сообщил о других коррелятах, которые по существу совпадают с диагностическими признаками группы Duanes. Однако, несмотря на эти точные диагностические описания и наблюдение, что у большинства пациентов действительно наблюдается экзофория вблизи, нарушение может возникать при наличии ортофории или даже эзофории (von Noorden, 1990). Неясно, требовал ли Дуэйн наличия астенопии для постановки диагноза КИ, и исследования показали, что наличие симптомов не является существенным для диагноза КИ (Capobianco, 1952; Cooper & Duckman, 1978).Тем не менее, интересно отметить, что клиницисты, представившие классические описания КИ, в то время не имели возможности провести различие между хорошо компенсированной и плохо компенсированной гетерофорией. Следовательно, определения Эванса (1997), описанные выше, добавляют полезное измерение к категоризации аномалий вергентности.
Некоторые авторы определили CI в терминах единственного знака, такого как удаленный NPC. Например, Летурно и др. (1979) диагностировали КИ, когда NPC находился на расстоянии более 10 см при измерении с помощью фонарика.Пиквелл и Стивенс (1975) сделали первоначальный диагноз CI, если стандартное измерение NPC было удаленным или конвергенция скачка была недостаточной. Другие, такие как Letourneau & Ducic (1988) и Scheiman et al (1996), использовали более одного признака для диагностики КИ. В наиболее полном обзоре Даум (1988) проанализировал 58 опубликованных статей и отметил значительные различия в критериях, используемых для определения КИ. Он обнаружил, что симптомы и снижение положительных резервов слияния на близком расстоянии были единственными критериями, названными более чем в половине рассмотренных исследований.Расширенный NPC и экзофория, которая была больше для ближнего, были критериями примерно в одной трети статей.
В обзоре литературы, проведенном Rouse et al (1998), сообщается, что оценки распространенности CI варьируются от 1,75 до 33,0% (Norn, 1966; Dwyer, 1992). Эта изменчивость может быть связана с вариациями в определении CI и различиями между выборками. Таблица 2 адаптирована из Rouse et al (1998) и суммирует некоторые исследования CI, описанные в литературе.
В исследовании 11 600 субъектов White & Brown (1939) предположили, что распространенность КИ составляет 7,5%. Хотя они использовали критерии Дуана для диагностики КИ, они не смогли предоставить описание популяции.
| Авторы | Год | Настройка | Возрастной диапазон (лет) | № | CI Критерии классификации | Частота CI (%) |
Бело-коричневый | 1939 | Офтальмология практика (?) | не сообщается | 11 600 | несложный КИ (нормы Дуана без вертикального отклонения) | 7.5 |
Кратка и Кратка | 1956 | Офтальмологический кабинет | не сообщается | 500 | 1 из 3 знаков 3 0f 3 знака (см. Обсуждение) | 25,0 12,5 |
Норн | 1966 | Офтальмологический кабинет | 6-70 | 10 022 | NPC> 9 см (кончик пальца) | 1.7 |
Махто | 1972 | Офтальмологический кабинет | <40 | 310 | NPC> 10 см | 11 |
Пиквелл и Стивенс | 1975 | Оптометрическая практика | 8-83 (75% старше 50 лет) | 200 | NPC> 10 см | 12.0 |
Letourneau et al | 1979 | Начальная школа | 7-14 | 735 | NPC> 10 см (фонарик) | 8,3 |
Пиквелл и Гэмпшир | 1981 | Оптометрическая практика | 5 до 80+ | 505 | ||
Letourneau & Ducic | 1988 | Начальная школа | 6-13 | 2,054 | Exophoria> на близком расстоянии и NPC> 10 см | 2.3 |
Дуайер | 1992 | Оптометрическая практика | 7-18 | 144 | некомпенсированный экзо по цене около | 33,0 |
Шейман и др. | 1996 | Оптометрическая клиника | 6-18 | 1,650 | NPC> 10 см перерыв или> 17.Восстановление 5 см и еще 3 знака | 5,3 |
Rouse et al | 1998 | Оптометрическая клиника | 8-12 | 620 | 3 степени важности (см. Обсуждение) | 17,6% (клинически значимо) |
Таблица 2.Резюме выбранных исследований КИ в нормальной клинической или школьной популяции ( адаптировано из Rouse et al, 1998).
Kratka и Kratka (1956) обследовали 500 пациентов и обнаружили распространенность 25% (n = 125), демонстрирующую по крайней мере одно обнаружение КИ, и 12,5% проявление экзофории у близких и удаленных NPC и снижение положительных резервов слияния. Они обнаружили, что 75% из 125 были симптоматическими, и сообщили, что у бессимптомных пациентов большая экзофория и удаленный NPC сопровождались отличными положительными резервами слияния.
Используя критерий NPC> 9 см, Норн (1966) обнаружил распространенность КИ 1,75% среди 10 022 населения в возрасте от 6 до 70 лет.
Mahto (1972) сообщил, что у 11% из 310 пациентов в возрасте до 40 лет NPC был больше 10 см. К этому исследованию следует относиться с большой осторожностью, поскольку целью, использованной для оценки конвергенции, был кончик пальца исследователя.
Используя либо удаленный NPC (разрыв> 10 см), либо плохую конвергенцию прыжков в качестве диагностических признаков, Пиквелл и Стивенс (1975) сообщили о распространенности ДИ 36% у 200 последовательных пациентов в возрасте от 8 до 83 лет.Распространенность пациентов, обращающихся исключительно с удаленным NPC, составила 12%.
Letourneau et al (1979) обследовали 735 детей в возрасте от 7 до 14 лет. Используя единый критерий NPC> 10 см, они обнаружили, что 8,3% детей
имел CI. Letourneau & Ducic (1988) впоследствии обследовали 2054 ребенка в возрасте от 6 до 13 лет и обнаружили, что у 2,3% проявлялись как минимум два признака ДИ.
Pickwell & Hampshire (1981) обследовали 505 последовательных пациентов, обращавшихся в оптометрическую практику.50 из них были исключены из исследования из-за явного косоглазия или активной патологии. NPC были измерены с помощью линии на черной карте, установленной на линейке ближней точки, чтобы получить точное расстояние. Кроме того, наблюдались скачкообразные конвергентные движения при изменении фиксации пациента с 6 м на 15 см. Из 455 пациентов, включенных в исследование, 110 (24,2%) показали плохую конвергенцию одним или обоими методами. 20% показали аномальную реакцию скачкообразного схождения. Дальнейший анализ распространенности различных реакций конвергенции скачка показан в таблице 3.
| Ответ | Количество пациентов | % пациентов |
Сходимости нет | 11 | 2,4% |
Медленное сходящееся движение | 44 | 9.7% |
Вариантное движение (один глаз фиксирует только около цели, другой — повернут) | 36 | 7,9% |
| Всего | 91 | = 20,0% |
Таблица 3. Распространенность типов неадекватной конвергенции прыжка у 455 пациентов ( из Pickwell & Hampshire, 1981).
Dwyer (1992) использовал критерий Шардса и характеристики кривых несоответствия фиксации для диагностики КИ и сообщил о распространенности 33% из 144 последовательных пациентов в возрасте от 7 до 18 лет, обращавшихся в его оптометрическую практику. Следует отметить, что такая выборка, скорее всего, будет высокоселективной.
Scheiman et al (1996) сообщили, что распространенность КИ составляет 5,3% от 1650 последовательных пациентов в возрасте от 6 до 18 лет, посещаемых оптометрической клиникой. Критерий, используемый для диагностики, основывался на наличии множественных клинических признаков.
Rouse et al (1998) изучали распространенность недостаточности конвергенции у детей в возрасте от 8 до 12 лет в оптических клиниках. Они обнаружили, что 17,6% детей были либо с определенным, либо с высоким подозрением на доверительный интервал в соответствии с их критериями, представленными в таблице 4.
| Признаки возможного КИ | Нет CI | Низкое подозрение CI | Высокий подозреваемый КИ | Определенный CI |
| Около экзофории ³ 4D , чем далеко | х | Ö + еще один знак | Ö + два других знака | Ö |
| Критерий разрушения | Ö | |||
| Положительная вергенция слияния <12D базовое размытие / 15 D базовый перерыв | Ö | |||
| NPC ³ 7.5 см до разрыва ИЛИ ³ Восстановление 10,5 см | Ö |
Таблица 4 Критерии, использованные Rouse et al (1998) для категоризации субъектов
В ретроспективном исследовании 179 пациентов в возрасте от 2 до 56 лет с дисфункцией бинокулярного зрения и экзо-отклонением для расстояния, близкого или обоих, Даум (1986a) разделил аномалии на три класса, а именно: (а) ДИ, ( б) равное экзо-отклонение на расстоянии и вблизи и (в) избыток дивергенции.Пациенты были классифицированы по соотношению дальности и ближнего угла отклонения. КИ оказался наиболее распространенным заболеванием. Эта группа была примечательна тем, что амплитуда аккомодации была снижена примерно на 3,0D ниже ожидаемого среднего значения. Кроме того, Даум сообщил, что КИ произошла в основном у женщин. Это также было более распространено у молодых пациентов и коррелировало с сообщениями о головных болях, нечеткости и астенопии. Другими связанными признаками были удаленный NPC и плохие положительные вергенции для ближнего.У этих испытуемых были хорошие стереопороги.
Как уже отмечалось, пациенты с КИ не обязательно страдают симптомами. фон Норден (1990) отмечает, что «для предотвращения астенопических симптомов и диплопии у человека есть встроенный механизм — подавление». Он предполагает, что супрессия наиболее активна для пациентов с гетерофорией и что именно по этой причине пациенты с гетерофорией «редко жалуются» на симптомы.
Этиология CI
Хотя фон Грефе предполагал, что КИ был миогенным (von Noorden, 1990), существуют неофициальные данные о психологическом или психосоматическом воздействии как причинном факторе в некоторых случаях (Taylor, 1990).Кнапп (1958) предположил, что если астенопические симптомы возникли недавно, следует исследовать возможную психологическую причину и при необходимости упомянуть психиатрическое вмешательство.
Hugonnier и Clayette-Hugonnier (1969) классифицировали этиологию КИ на пять категорий:
- Анатомическое (например, большое межзрачковое расстояние) или паретическое происхождение (например,
миастения)
(б) Замедление развития
(c) Глазные причины.«Диссинергия» аккомодации и конвергенции в
г.нескорректированная миопия, анизометропия, очень высокая гиперметропия, высокий
астигматизм и пресбиопия исправлены впервые. Другие причины в этой категории — амблиопия и односторонняя слепота.
- Общие физические причины. К ним относятся «интоксикации» и заболевания
эндокринных желез (например, признак Мебиуса при офтальмопатии щитовидной железы).
- Психологические причины.Они упоминались выше и могут включать тревогу и невроз.
Lyle & Bridgeman (1959) предполагают, что существует семь типов CI
1. первичный
2. Превышение вторичной дивергенции по отношению к первичной
3. вторичный по отношению к вертикальному дисбалансу мышц
4. преломляющая
5. связано с общей слабостью или стрессом
6 пресбиопия
7.послеоперационный, например, вторичный после тенотомии медиальной прямой мышцы
Сообщалось также о более конкретной этиологии, включая связь с «хлыстовыми травмами», вызванными дорожно-транспортными происшествиями (Anderson, 1961), анемией (Manson, 1962) и травмой головы (Carroll & Seaber, 1974).
Лечение аномалий конвергенции
Оптометристы имеют несколько вариантов лечения, доступных для управления ассоциированными аномалиями фории и конвергенции.К ним относятся ортоптика или терапия зрения, оптическое вмешательство (как линзы, так и призмы) и хирургия.
Призмы
Использование призм может быть рассмотрено, когда ортоптическое лечение нецелесообразно из-за плохого состояния здоровья или из-за недостатка времени или стимула со стороны пациента. Существует множество способов определения амплитуды призмы. Распространенным методом назначения в Великобритании является определение количества призмы, необходимого для устранения несоответствия фиксации.Может быть предписана минимальная призма, необходимая для нейтрализации несоответствия фиксации (Mallett, 1966).
Evans (1997) предложил объективный метод определения силы призмы, с помощью которого практик определяет силу самой слабой призмы, необходимую для быстрого и плавного восстановления после испытания прикрытия. Этот метод предполагает, что плохо компенсированная гетерофория действительно вызывает медленное и прерывистое восстановление во время теста покрытия. Это предположение основано на анекдотических свидетельствах и будет исследовано в данной диссертации.
Призмытакже можно использовать при лечении расходящегося косоглазия (Ravault et al, 1968; Berard, 1968). Раво и др. Предположили, что устранение подавления является основным эффектом постоянного ношения призматической коррекции у тех пациентов, для которых призматическая терапия устраняет явное отклонение.
Сообщалось, что рельеф вертикальной гетерофории с помощью призмы способствует компенсации экзофории (London & Wick, 1987).
Призма адаптации обычно происходит у пациентов с нормальным бинокулярным зрением.Однако у большинства пациентов с аномалиями бинокулярного зрения, которые вызывают симптомы, наблюдается аномальная призматическая адаптация (North & Henson, 1981). Хотя это может быть показанием для назначения призм, North & Henson (1982; 1992) показали, что некоторые пациенты, у которых была аномальная адаптация к призмам до лечения, имели нормальную адаптацию призм после лечения.
Winn (1994) продемонстрировал, что адаптация призмы с возрастом снижается, и предположил, что это может, по крайней мере, частично объяснить утверждение о том, что пожилые пациенты не реагируют на ортоптические упражнения так же хорошо, как молодые пациенты.
Линзы
Следует рассмотреть вопрос о том, может ли коррекция аметропии или анизометропии пациента способствовать улучшению бинокулярной функции. Размытие одного или обоих глаз может привести к ухудшению компенсации гетерофории. В то время как Уквад и Беделл (1993) обнаружили, что небольшая степень размытия и уменьшение контраста будут иметь несущественное влияние на способность фиксации или вергентность, Дуайер и Вик (1995) обнаружили, что даже коррекция низкой степени аметропии может значительно улучшить вергентность и аккомодационную функцию у некоторых людей. пациенты.
Изменение рецепта на очки может снизить глазодвигательный стресс. Это эффективно использует взаимосвязь между аккомодацией и аккомодационной вергенцией для увеличения или уменьшения конвергенции. Для пациента с плохо компенсируемой эзофорией, близкой к избытку конвергенции или ее избытку, можно использовать дополнительную положительную линзу, чтобы уменьшить потребность в аккомодации и, таким образом, уменьшить аккомодационную конвергенцию. Это приведет к уменьшению амплитуды эзофории. Дополнительная положительная линза вызовет нечеткость зрения вдаль, поэтому часто используются линзы бифокального типа.Добавление в ближний сегмент дает пациенту преимущество в уменьшении потребности в аккомодации для зрения вблизи. Точно так же добавление бинокулярных отрицательных линз (Caltrider & Jampolsky, 1983) может облегчить плохо компенсируемую экзофорию. Это вызовет дополнительный аккомодационный спрос и, таким образом, будет стимулировать аккомодационную вергенцию. Тот факт, что этот метод требует дополнительного приспособления, означает, что его можно использовать только для пациентов с адекватным приспособлением. У молодых пациентов эту технику можно использовать, чтобы помочь контролировать связанную экзофорию на расстоянии и вблизи, а также избыток расхождения и недостаточность конвергенции.
Следует отметить, что пациенты могут адаптироваться к сферическим линзам так же, как они могут адаптироваться к призмам (North & Henson, 1985). Таким образом, пациентам следует разрешить носить предложенный рецепт в течение 3-5 минут и повторно оценить моторный баланс глаз, чтобы убедиться, что адаптация не произошла (Evans, 1997).
Dwyer (1992) оценил рефракцию, вергенцию и аккомодационный статус 144 последовательных пациентов и обнаружил, что 39% имели аметропию.Из них почти у 80% наблюдалась вергенция и / или аккомодационная аномалия. Dwyer & Wick (1995) рекомендовали использовать коррекцию рефракции для таких пациентов и предположили, что существует вероятность того, что этот тип вмешательства приведет к пассивному разрешению бинокулярного расстройства.
Ортоптические упражнения
В Великобритании термин «ортоптика» используется для описания глазных упражнений для лечения глазных моторных расстройств, таких как аномалии вергентности.Ортоптика — это термин, который используют оптометристы и больничные ортоптики. В США термин «ортоптик » имеет тенденцию описывать лечение, предлагаемое отдельными ортоптиками, а терапия зрения (или зрительная терапия) используется для описания режимов упражнений, предписываемых оптометристами. Для большинства режимов упражнений эти два термина, вероятно, описывают очень похожие принципы лечения. В целях данного обсуждения эти два термина будут использоваться как взаимозаменяемые, чтобы учесть различные употребления в международной литературе.
Термин ортоптика происходит от греческого или о s означает «прямой», а op т я k о z означает «относящийся к зрению». Ортоптика уже много веков используется для лечения глазных двигательных нарушений. Флик (1937) (цитируется Джайлсом, 1943) упоминает о лечении косоглазия с помощью маски еще в папирусе Эберса, датируемом примерно 1650 годом до нашей эры. Флик предположил, что первое ортопедическое лечение было проведено Аегинцом (625-690 гг.).
Методы
Виды тренировки зрения или ортопедических упражнений очень широки и разнообразны. Некоторые из наиболее часто назначаемых упражнений при недостаточности конвергенции и экзофорических состояниях — это «отжимания», «конвергенция в прыжке» и «техники физиологической диплопии».
Упражнения отжимания (карандаш к носу)
Пациента просят посмотреть на тонкий кончик карандаша, расположенный на расстоянии около 50 см или далеко за пределами досягаемости NPC.Затем карандаш перемещается к глазам до тех пор, пока он не станет двойным, или практикующий не заметит, что один глаз перестал сходиться (Evans, 1997). Упражнение повторяется несколько раз с целью развития конвергенции и уменьшения NPC. Если пациент не ценит диплопию, практикующий должен помочь пациенту развить понимание физиологической диплопии, прежде чем продолжить. Как только пациент поймет упражнение, пациенту могут быть даны инструкции выполнять упражнения дома на ежедневной основе.
Упражнения на конвергенцию в прыжке
Пациент подвигает маленькую детализированную цель как можно ближе, прежде чем она станет нечеткой, двойной или один глаз не расстанется. Мишень удерживается неподвижно, и пациент расслабляет аккомодацию и конвергенцию, чтобы рассмотреть цель на расстоянии. Затем фиксация изменяется с расстояния на ближайшую цель. Пациент должен знать о физиологической диплопии (Evans, 1997). Этот цикл повторяется заданное количество раз.
Методы физиологической диплопии
Есть несколько вариаций этой категории упражнений. Например, пациента можно проинструктировать держать два карандаша разных цветов на разных расстояниях по средней линии на простом фоне. Пациенту предлагается посмотреть на следующий карандаш, который следует рассматривать отдельно. Более близкий карандаш должен выглядеть двойным. Затем пациенту предлагается просмотреть ближайшую цель, которая должна быть единственной.Дальнейшую цель следует тогда видеть в диплопии. Затем эту процедуру повторяют, приближая карандаши к пациенту.
Другой вариант включает использование веревки, на которую нанизано несколько маленьких бусинок. Пациенту предлагается держать шнур так, чтобы один конец касался кончика носа, а другой конец находился на расстоянии вытянутой руки. Пациент зацикливается на самой дальней бусине, которая должна быть видна отдельно. Пациент также должен воспринимать нить и оставшуюся часть бус в диплопии, причем разделение двух изображений становится больше по мере приближения нити к носу.Затем пациент повторно фиксируется на следующей бусине. Теперь этот должен быть виден по отдельности, причем самая дальняя бусинка и более близкие бусинки видны в диплопии. Диплопические изображения струны должны пересекать единственную бусину. Пациенту предлагается изменить фиксацию и продвигаться от бусинки к бусине, пока ближайшая бусинка не будет видна отдельно.
В аналогичной технике используется карта, на которой нарисованы линия и серия точек в качестве альтернативы веревке и бусинкам.
Другая техника
Разработка фузионных резервов может проводиться с использованием гаплоскопических инструментов или векторов (Rosner & Rosner, 1990; Evans, 1997). Упражнения Института свободного пространства (Evans, 1998) специально разработаны для пациентов, которые могут выполнять их дома, и их можно получить в Институте оптометрии в Лондоне.
Афандор (1982), Goldrich (1982), Scheiman et al (1983) и Letourneau & Giroux (1984) сообщили об успехе в лечении больших экзо-отклонений с помощью окуломоторной биологической обратной связи.Компьютеризированная терапия вергентности также применялась при лечении глазодвигательных расстройств (Sommers et al, 1984; Daum et al, 1987).
Эффективность
Ортоптические упражнения уже много лет используются как традиционный или «ортодоксальный» метод лечения. Широко признано, что тренировочные упражнения слияния резерва могут быть эффективным методом лечения положительной дисфункции слияния резерва, такой как недостаточность конвергенции (Davies, 1956; Kratka & Kratka, 1956; Passmore & MacLean, 1957; Norn, 1966; Wick, 1977; Cooper. & Duckman, 1978; Kertesz, 1982; Daum, 1982; Pantano, 1982; Cooper et al, 1983; Cohen & Soden, 1984; Daum, 1984a; Daum, 1984b).Другие исследования направлены на то, чтобы показать, что пациенты, получающие вергентную подготовку, эффективно избавляются от трудностей, связанных с другими глазодвигательными аномалиями (Ludlam & Kleinman, 1965; Sanfillipo & Clahane, 1970; Hoffman, 1973).
Goodson & Rahe (1981) изучали влияние тренировки зрения на различные оптометрические параметры, в том числе на дальность вергенции, в группе пилотов ВВС США с нормальным бинокулярным зрением. Была контрольная группа, которая не проходила никакой тренировки зрения, и исследование было замаскированным для одного (практикующего), но для обработанной группы не применялся контроль плацебо.Они сообщили о значительном (p <0,05) увеличении в тренированной группе для исходной вергентности к размытию и разрыву и базы в вергентности к восстановлению.
Даум (1982) изучал временной ход и величину изменений в системе горизонтальной вергентности субъектов с нормальным бинокулярностью, следуя режимам обычно используемых техник тренировки вергенции. Тридцать пять здоровых взрослых людей в возрасте от 22 до 28 лет прошли полное обследование рефракционной, бинокулярной и глазодвигательной систем.Затем все они прошли визуальную тренировку, которая состояла из двух сессий (в общей сложности 4 мин / день) упражнений «отжимания», упражнений с перевертыванием призмы или прыжка (2 мин), упражнений с переменным вектографом (2 мин) и тренировки вергентности на большом амблиоскопе. (2 мин). Все упражнения, кроме последнего, выполнялись дома пять дней в неделю в течение трех недель. Анализ результатов показал, что положительные диапазоны слияния значительно увеличиваются после 1 недели тренировок с еще большим эффектом, который можно измерить через три недели.Через шесть месяцев после прекращения тренировок эффект от упражнений все еще был очевиден, но было обнаружено, что способность к вергентности уменьшилась. В то время как отрицательные диапазоны слияния увеличились, это обучение было менее эффективным.
Долгосрочный эффект упражнений, о котором сообщалось у здоровых субъектов (Daum, 1982), также был продемонстрирован для CI Пантано (1982), исследование которого предложило долгосрочное лечение недостаточности конвергенции. Сразу после обучения двести семь пациентов с КИ сравнивали на основе их категории успеха.Те, кого отпустили как «вылеченные», сохранили тот же результат через шесть месяцев и два года. Из этих пациентов в группе «частично вылеченного» у 79% симптомы оставались бессимптомными через шесть месяцев, но только у 11% симптомы отсутствовали через два года. Группа «неудачников» не получала симптоматического облегчения, и даже улучшенные навыки конвергенции не поддерживались через шесть месяцев после терапии. Только те пациенты, которые смогли достичь как произвольной, так и слитной конвергенции и которые научились адекватно расслаблять аккомодацию во время конвергенции, так что они изменили соотношение AC / A, могли сохранять свой статус с течением времени.
Даум (1983b) сравнил эффективность тренировки шага и прыжка (фазовой) вергентности с процедурами скольжения и отжимания (тоническая) вергентности в группе из тридцати четырех здоровых бессимптомных взрослых, которые были случайным образом разделены на две группы. Одна группа выполняла фазовую тренировку, а другая — групповую тренировку тонической вергенции. В то время как обе группы добились значительных успехов в диапазонах сходимости и расхождения, фазовая группа показала наибольшее улучшение. Стоит отметить, что Пиквелл и Стивенс (1975) предположили, что скачкообразная (фазовая) конвергенция может иметь большее клиническое значение, чем плохой NPC, а Пиквелл и Хэмпшир (1981) продемонстрировали более сильную связь между симптомами и плохой конвергенцией прыжков, чем с плохим NPC.
Daum (1982) и Vaegan (1979) также продемонстрировали эффективность повторяющихся коротких тренировочных периодов.
Однако на удивление мало исследований, критически оценивающих эффективность различных методов. Еще меньше исследований, в которых используются плацебо-контролируемые испытания с двойной маской, например, проведенные Даумом (1986c), и перекрестный дизайн контрольной группы с подобранными субъектами, использованный для уменьшения эффекта плацебо в исследовании, описанном Купером и др. (1983).
Купер и др. (1983) использовали дизайн кроссовера контрольной группы с подобранными субъектами в исследовании эффектов автоматизированной тренировки конвергенции резерва слияния на группе из семи пациентов с КН. У всех пациентов наблюдалось значительное увеличение диапазона вергентности с одновременным заметным уменьшением симптомов после тренировки. Их результаты ясно продемонстрировали эффективность тренировки фузионного резерва в снижении астенопии у этих пациентов. Последующая тренировка аккомодации и вергенции с использованием традиционных ортопедических процедур привела к дальнейшему снижению астенопии, а также к увеличению диапазонов положительного слияния.
Даум (1986c) провел двойное слепое плацебо-контролируемое исследование, чтобы изучить эффекты позитивной тренировки слияния резерва. Было выбрано четыре экспериментальных протокола, и по пять человек были случайным образом распределены в каждую из четырех экспериментальных групп. Каждый испытуемый в каждой группе провел в общей сложности 120 минут в течение трехнедельного периода, выполняя тренировку слияния резерва. Группа А провела двенадцать 10-минутных занятий; Группа B за шесть 20-минутных занятий; Группа D была контрольной и выполняла упражнения на версии, а не на вергентность.Все тренинги проходили в оптометрической клинике и состояли из тренировок по положительному слиянию с синоптофором. Каждая из тестовых групп показала увеличение их способности к положительному слиянию как на расстоянии, так и вблизи, при этом группа, проводившая более короткие сеансы, демонстрировала наибольший общий рост. Эта группа также была единственной группой, которая продемонстрировала значительное увеличение положительных результатов размытия и отрицательных резервов слияния. В контрольной группе достоверного изменения амплитуд вергентности не наблюдалось.Стоит отметить, что, хотя это исследование показало, что можно увеличить количество положительных вергентностей слияния, оно не имело целью показать, что увеличение положительных вергентностей слияния эффективно при лечении астенопических симптомов, вызванных дисфункцией вергенции.
Хотя более молодые пациенты могут иметь тенденцию более положительно реагировать на такие упражнения, чем пациенты старшего возраста (Winn et al, 1994), Wick (1977), используя четко определенные и строгие критерии успеха, сообщил о 93% излеченности после лечения 191 пресбиопии. в возрасте от 45 до 89 лет с астенопическими симптомами, связанными с недостаточностью конвергенции, экзофорией ближней точки и / или дефицитом слитной вергенции.Аналогичные результаты были получены для взрослых старше 60 лет с недостаточностью конвергенции (Cohen & Soden, 1984). Это говорит о том, что практикующие врачи не должны полагаться на возраст пациентов при определении того, следует ли назначать ортопедические упражнения. В самом деле, Гришем (1988) предположил, что из-за своей зрелости пациенты старшего возраста могут демонстрировать самодисциплину, необходимую для завершения визуальной терапии.
Хирургия
Хирургическое вмешательство может потребоваться при больших отклонениях угла наклона, а также при различных сопутствующих аномалиях, которые не поддаются или вряд ли поддаются лечению другими методами.
 Межзрачковое расстояние
Межзрачковое расстояние  Углы 5 метров. Для диаметра 6 см угол 2,5 метра равняется 15 призматическим диоптриям, где
Углы 5 метров. Для диаметра 6 см угол 2,5 метра равняется 15 призматическим диоптриям, где  Ближняя фория построена аналогичным образом относительно линии спроса, где она пересекает уровень стимула аккомодации 2.5D. Линия, соединяющая две меры фории, называется линией фории, и она предсказывает форию на всех расстояниях просмотра.Фория означает разделение линий фории и спроса.
Ближняя фория построена аналогичным образом относительно линии спроса, где она пересекает уровень стимула аккомодации 2.5D. Линия, соединяющая две меры фории, называется линией фории, и она предсказывает форию на всех расстояниях просмотра.Фория означает разделение линий фории и спроса.
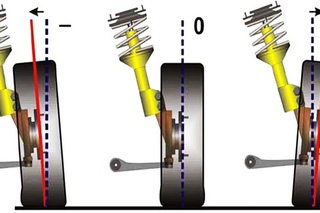 Целью этих тестов является измерение ширины зоны четкого единичного бинокулярного зрения (ZCSBV), которая указывает диапазон фузионной вергенции. Этот диапазон почти одинаков для дальних и ближних расстояний. Наблюдается небольшое увеличение положительной фузионной конвергенции (PFC) вблизи из-за проксимальной конвергенции. Слияние конвергенции рассчитывается как сумма относительной конвергенции и фории:
Целью этих тестов является измерение ширины зоны четкого единичного бинокулярного зрения (ZCSBV), которая указывает диапазон фузионной вергенции. Этот диапазон почти одинаков для дальних и ближних расстояний. Наблюдается небольшое увеличение положительной фузионной конвергенции (PFC) вблизи из-за проксимальной конвергенции. Слияние конвергенции рассчитывается как сумма относительной конвергенции и фории: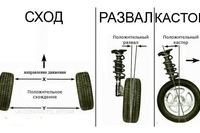 22.4
22.4  Во время испытания амплитуды призмы для размытия, разрыва и восстановления отмечаются и наносятся на график. Относительную вергенцию следует измерять после измерения форий, чтобы избежать воздействия протоков на фории. Перед измерением боковых каналов необходимо скорректировать вертикальные фории.
Во время испытания амплитуды призмы для размытия, разрыва и восстановления отмечаются и наносятся на график. Относительную вергенцию следует измерять после измерения форий, чтобы избежать воздействия протоков на фории. Перед измерением боковых каналов необходимо скорректировать вертикальные фории.  В случае высокого отношения AC / A или узкого диапазона слитной вергенции, изменения фории могут потребовать большей слитной вергенции, чем доступно, и, как следствие, пациент не сможет в такой степени увеличить или уменьшить аккомодационную реакцию. в условиях бинокля, как и в условиях монокуляра. В результате изменения фории могут не корректироваться слиянием слитной вергенции. Эти точки данных могут использоваться для помощи в построении пределов BI и BO или высоты ZCSBV.
В случае высокого отношения AC / A или узкого диапазона слитной вергенции, изменения фории могут потребовать большей слитной вергенции, чем доступно, и, как следствие, пациент не сможет в такой степени увеличить или уменьшить аккомодационную реакцию. в условиях бинокля, как и в условиях монокуляра. В результате изменения фории могут не корректироваться слиянием слитной вергенции. Эти точки данных могут использоваться для помощи в построении пределов BI и BO или высоты ZCSBV.