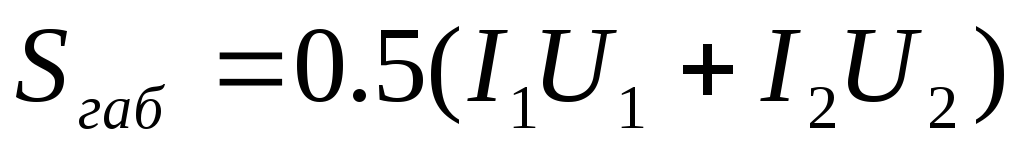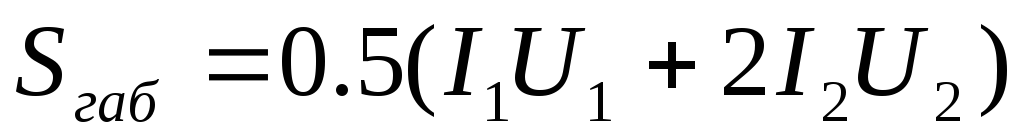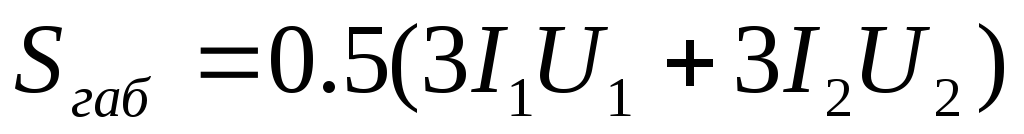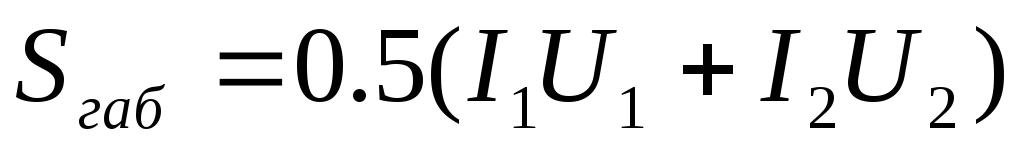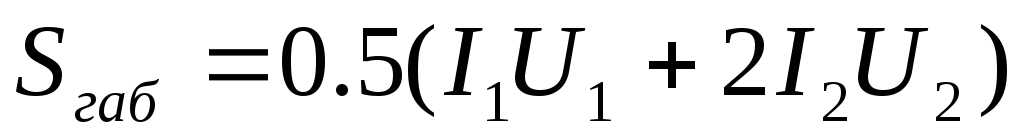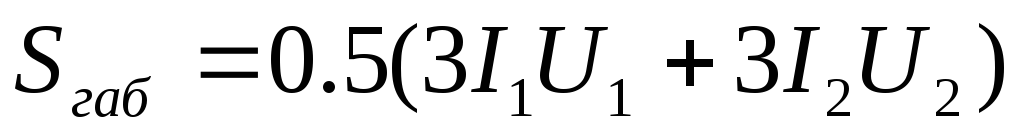Особенности работы выпрямителей, или как правильно рассчитать мощность силового трансформатора — Начинающим — Теория
Хороший и надёжный силовой трансформатор — это уже половина собираемой и разрабатываемой конструкции.
В настоящее время выбор силовых трансформаторов, предлагаемых рынком, для радиолюбителей довольно широк. Но не смотря на это, не все предлагаемые трансформаторы идеально подходят для нужд радиолюбителя (по току, напряжению, количеству обмоток и т.д.), и поэтому довольно часто ему приходится самостоятельно изготавливать силовые трансформаторы для своих разработок и собираемых конструкций.
В этой статье я попробую объяснить, как правильно выбрать, или рассчитать силовой трансформатор для своей конструкции.
Нового я здесь ничего не открою, и постараюсь как можно проще и на примерах, объяснить Вам то, что уже давно доказано и решено. Просто в силу каких либо обстоятельств, не все это могут знать.
В основном радиолюбителю приходится изготавливать силовые трансформаторы средней мощности 50 — 300 Вт.
КПД таких трансформаторов достигает 0,88 — 0,92. У более мощных промышленных трансформаторов, при мощностях более 1 кВт, КПД может достигать 0,97-0,98, так как обмотки их намотаны толстым проводом и потери в них на активное сопротивление минимальны.
Чтобы правильно рассчитать трансформатор, нужны довольно сложные вычисления, радиолюбители-же пользуются для этих целей упрощёнными формулами и радиолюбительскими программами, которые в принципе тоже довольно точно позволяют это сделать, поэтому я тоже постараюсь не отходить от этой традиции и всё попробую объяснить на практических примерах и готовых расчётах, используя по минимуму формулы и вычисления.
Как обычно производится расчёт силового трансформатора.
Зная напряжение и ток, который должна давать вторичная (или несколько вторичных) обмотка (U2 и I2), находим мощность вторичной цепи: При наличии нескольких вторичных обмоток мощность подсчитывают путем сложения мощностей отдельных обмоток.
Отсюда можно найти и мощность первичной обмотки, где для трансформаторов средней мощности к нашим расчётам мы берём КПД трансформатора 0,9 (90%). Для трансформаторов меньшей мощности соответственно и КПД берётся меньше (0,8).
Мощность первичной обмотки Р1 (мощность трансформатора) в этом случае будет равна;
То есть поясню, если расчётная мощность вторичной (вторичных) обмотки у нас получилась например 100 Вт, то общая мощность трансформатора будет равна 111,1 Вт (100/0,9). Это ещё не учитывая ток холостого хода, который тоже прибавляется к общей мощности трансформатора.
Как определить мощность первичной обмотки мы уяснили, теперь как правильно определить мощность вторичной обмотки?
Для этого у нас имеется какая либо нагрузка, которая потребляет определённый ток при определённом напряжении. Например имеется нагрузка, потребляющая ток 2 Ампера при напряжении 15 Вольт.
Если же вторичная обмотка нагружена на нагрузку через элементы выпрямителя, или выпрямителя и фильтра, то ситуация приобретает совсем другой оборот. Ток отдаваемый вторичной обмоткой будет больше тока, потребляемого нагрузкой!
Почему так, давайте попробуем вместе с этим разобраться.
Работа вторичной обмотки на активную нагрузку мы рассматривать не будем, здесь всё ясно, давайте пойдём дальше.
Работа выпрямителя на активную нагрузку.
Однополупериодный выпрямитель.
Поставим перед нагрузкой выпрямительный диод. То есть у нас получился однополупериодный выпрямитель.
Соберём такую же схемку. Трансформатор у меня тороидальный, мощностью 60 Вт, с напряжением ХХ вторичной обмотки около 20 вольт (номинальный ток нагрузки 3,8 А, номинальное напряжение 16,5 Вольт), ток ХХ трансформатора 7 мА.
В разрыв первичной обмотки, для измерения её тока, я поставил резистор, величиной 1,0 Ом, в разрыв вторичной (последовательно с нагрузкой) резистор, величиной 0,1 Ом. Для измерения в цепях переменного и пульсирующего тока и напряжения, я использовался среднеквадратичный (RMS) микровольтметр В3-57, ну и для измерения в цепях постоянного тока — цифровой мультиметр «Mastech MY64».
Для безопасности измерений, вся эта конструкция подключалась через разделительный трансформатор. В качестве нагрузочных резисторов использовались проволочные переменные сопротивления различных величин, мощностью 25 Вт.
Действующий ток нагрузки был установлен 0,5 ампер (рисунок выше). Предел измерения 100 мВ, шунт во вторичной цепи 0,1 Ом.
Измерим ток, потребляемый первичной обмоткой.
Ток первичной обмотки получился 97 мА, минус 7 мА ХХ, итого 90 мА. Напряжение на первичной обмотке 215 вольт. Мощность потребляемая первичной обмоткой получилась 19,35 Вт, то есть в 4 (четыре) раза больше мощности потребляемой нагрузки. Почему так? Кому интересны все подробности происходящих процессов в трансформаторе, рекомендую почитать первоисточники, приведённые в конце статьи, кому лень читать, попробую объяснить по простому.
При установке диода последовательно с нагрузкой, у нас получается однополупериодный выпрямитель. На нагрузку подаётся импульс напряжения (тока) только в положительный полупериод, а в отрицательный ничего нет (пауза). В результате чего среднее напряжение на нагрузке уменьшается более, чем в два раза (точнее в 2,2) по сравнению с напряжением на вторичной обмотке. Средний ток через диод соответствует току нагрузки, а действующий ток диода и самой вторичной обмотки — больше тока нагрузки в 1,57 раза.
Ток нагрузи 0,5 А, умножаем на 1,57=0,785 (ток вторичной обмотки). Полученный ток умножаем на напряжение вторичной обмотки (19 Вольт) 0,785х19=14,9 Вт — это получается отдаваемая мощность вторичной обмотки, плюс сюда ещё добавляются и переходные процессы при работе диода (вентиля), плюс реактивные токи, которые просто нагревают обмотку, в итоге мощность трансформатора получается минимум в 3,5 раза больше мощности потребляемой нагрузкой.
Ещё при работе этой схемы во вторичной обмотке возникает постоянная составляющая (из-за того, что ток в обмотке протекает только в одном направлении в один полупериод), которая намагничивает сердечник трансформатора и тем больше, чем больше ток нагрузки. Из-за этого свойства сердечника ухудшаются и увеличивается ток ХХ, в последствии чего повышается потребляемая мощность трансформатора (у нас получилась мощность в 4 раза больше).
Например уже при токе нагрузки в 1,0 Ампер, напряжение на нагрузке получилось 9,0 Вольт, сопротивление нагрузки 9,0 Ом, мощность нагрузки 9,0 Вт. Ток первичной обмотки получился 230 мА (минус 7 мА) итого 223 и напряжение на первичной обмотке 210 вольт. Итоговая потребляемая мощность трансформатора 46,83 Вт, то есть больше мощности потребляемой нагрузкой уже в 5,2 раза. Сильно увеличился ток ХХ с увеличением тока нагрузки (от которого увеличилось намагничивание сердечника).
Двухполупериодный выпрямитель.
Ну, с однополупериодным выпрямителем разобрались, давайте пойдём дальше. Посмотрим как ведёт себя двухполупериодная схема.
Что из себя представляет двухполупериодная схема выпрямителя. Это два однополупериодных выпрямителя, которые работают на общую нагрузку. Каждый выпрямитель имеет свою обмотку, но в отличии от другого — противофазную, в результате чего выпрямляются (поступают в нагрузку) оба полупериода, за счёт чего эффективность такого выпрямителя, по сравнению с однополупериодным, повышается два раза.
Посмотрим, как он себя ведёт. Соберём схему двухполупериодного выпрямителя. Для этой схемы нужен трансформатор с отводом от средней точки вторичной обмотки. Трансформатор другой, вторичная обмотка имеет напряжение 193-193 Вольт, ток ХХ у него 36 мА (какой нашёл).
Проволочными резисторами выставил ток нагрузки 150 мА.
Нагрузочный резистор получился с сопротивлением 1,17 кОм, измеренное напряжение на нём 175 Вольт. Мощность потребляемая нагрузкой получилась 26,17 Вт. Смотрим ток первичной обмотки.
Ток первичной обмотки 210 мА, минус ток ХХ (36) итого 174 мА. Мощность потребляемая трансформатором получилась 38,28 Вт. Это больше мощности потребляемой нагрузкой в 1,46 раз.
Идём дальше.
Мостовая схема выпрямителя.
Проверим, как поведёт себя мостовая схема выпрямителя.
Для этого соберём следующую схему.
Трансформатор возьмём тот, что был и раньше, с одной вторичной обмоткой из первого рассматриваемого случая для однополупериодного выпрямителя.
Ток нагрузки я выставил 0,5 А, проволочное переменное сопротивление получилось величиной 32 Ома. Напряжение на нагрузке 16 Вольт. Мощность потребляемая нагрузкой получилась 8 Вт.
Смотрим ток потребляемый первичной обмоткой.
Ток первички 53 мА минус ток ХХ (7 мА) = 45 мА. Мощность потребляемая первичной обмоткой получилась 9,9 Вт. Это в 1,23 раза больше, чем мощность потребляемая нагрузкой.
Как видите, здесь показатели ещё лучше, чем у двухполупериодного выпрямителя, не говоря уже об однополупериодном.
Работа выпрямителя на нагрузку с ёмкостной реакцией.
В основном радиолюбители используют в своей практической деятельности выпрямители с сглаживающими фильтрами, начинающимися с ёмкости (конденсатора), то есть нагрузка с ёмкостной реакцией.
Переписывать учебники не имеет смысла, кому интересно, список литературы в конце статьи. Просто я здесь дальше кратко изложу основные схемы выпрямителей применяемых радиолюбителями, их особенности и приближённые электрические характеристики, и как они влияют на общую мощность трансформатора.
Однополупериодный выпрямитель.
Начнём как обычно с однополупериодного выпрямителя.
У такого выпрямителя конденсатор фильтра заряжается до амплитудного значения напряжения вторичной обмотки (при отсутствии нагрузки). То есть если напряжение вторички 10 Вольт, то конденсатор зарядится до 10х1,41=14,1 Вольта (это без падения напряжения на диоде).
Простота схемы, используется всего один вентиль (диод, кенотрон).
Недостатки;
Большая зависимость выходного напряжения от тока нагрузки, пониженная частота пульсаций по отношению с другими схемами, что требует применение конденсаторов в два раза большей ёмкости, плохое использование трансформатора (низкий КПД), присутствует вынужденное намагничивание сердечника. При пробое вентиля, переменное напряжение поступает на конденсатор, что ведёт его к выходу из строя и взрыву.
Особенности схемы;
Применяется радиолюбителями для питания слаботочных цепей. Обратное напряжение в этой схеме прикладываемое к вентилю, приблизительно в три раза больше напряжения вторичной обмотки (точнее в 2,82 раза), почему так происходит — попробуйте сами определить. То есть если у Вас вторичка имеет напряжение 100-110 Вольт, то диод необходимо ставить на обратное напряжение не менее 400 Вольт, на 300 Вольт может пробить.
Средний ток через вентиль здесь соответствует току нагрузки, а действующее значение тока через вентиль в два раза больше тока нагрузки.
Вторичная обмотка для однополупериодного выпрямителя выбирается в 1,8 -1,9 раз больше по току (лучше в 2 раза), чем ток потребления нагрузки. К общей расчётной мощности трансформатора, если есть ещё другие обмотки, добавьте мощность этой Вашей нагрузки умноженной на 2.
Двухполупериодный выпрямитель.
Двухполупериодный выпрямитель обладает гораздо лучшими параметрами, чем однополупериодный. Выходное напряжение этого выпрямителя (напряжение на конденсаторе) в 1,41 раз выше, чем напряжение вторичной обмотки (половины). Это при отсутствии нагрузки.
Достоинства выпрямителя;
Малое количество используемых вентилей (2). Среднее значение тока через вентиль почти в два раза меньше тока нагрузки. Уровень пульсаций у этой схемы в 2 раза меньше по сравнению с однополупериодной схемой выпрямления. Емкость конденсатора при одинаковом с однополупериодной схемой коэффициенте пульсаций, может быть в 2 раза меньше. Отсутствует вынужденное намагничивание сердечника, но это зависит от конструкции трансформатора и способа намотки обмоток, о чём будет сказано ниже.
Недостатки;
Сложная конструкция трансформатора, вторичная обмотка состоит из двух половин, откуда не рациональное использование меди. Обратное напряжение на один вентиль здесь также больше напряжения (половины) вторичной обмотки в 2,82 раза. Плохое использование трансформатора, так как общая расчётная мощность всей вторичной обмотки получается в 2,2 раза больше мощности потребляемой нагрузкой.
Особенности схемы;
Так как за один период, в этой схеме работают обе половины вторичной обмотки по очереди, соответственно и вентили (диоды) тоже работают по очереди, то среднее значение тока через один вентиль (за период) здесь получается почти в два раза меньше, чем ток нагрузки. То есть например, если поставить в эту схему диоды с допустимым постоянным током на 5 Ампер, то снять с этого выпрямителя можно будет 7-8 Ампер без особого риска выхода из строя диодов, естественно обеспечив им необходимое охлаждение. Действующий же ток через вентиль и вторичную обмотку здесь будут в 1,1 раза больше тока нагрузки.
Провод для вторичной обмотки в этой схеме, можно выбирать на 30-40% меньше по току (сечение), чем ток нагрузки, так как половины вторичной обмотки так же работают по очереди и среднее значение тока вторичной обмотки получается меньше тока нагрузки. Но лучше, если позволяют размеры трансформатора и возможности, мотать вторичку проводом соответствующего сечения с током нагрузки.
Насчёт вынужденного намагничивания сердечника. Если сердечник трансформатора Ш-образный, броневой, и все обмотки размещены на одном каркасе, то вынужденного намагничивания сердечника здесь не будет.
Если сердечник трансформатора стержневой и в конструкции трансформатора предусмотрены два каркаса, на которых размещены обмотки, и сетевая обмотка состоит из двух половин, размещённых на разных стержнях (ТС-180, ТС250), то вторичную обмотку в таких трансформаторах необходимо выполнять следующим образом;
Каждая половина вторичной обмотки делится ещё раз пополам и наматывается на разных стержнях, потом всё соединяется последовательно, сначала четверти одной половины, затем другой. Как ниже на рисунке. Иначе будет намагничивание сердечника.
Так как кенотроны обладают большим внутренним сопротивлением, то при выборе кенотронной схемы выпрямителя, напряжение вторичной обмотки (половины) выбирается в среднем примерно на 10-15% меньше планируемого выходного напряжения выпрямителя. Это ещё зависит от тока нагрузки. Чем больше ток нагрузки, тем меньше должна быть разница.
Ещё запомните, что во всех выпрямителях и с кенотронами и с диодами, конденсаторы фильтра при отсутствии нагрузки, всегда заряжаются до амплитудного напряжения вторичной обмотки (UC = U2 x 1,41). Это учитывайте при выборе напряжения конденсаторов фильтра.
Как примерно определить здесь, какая мощность добавится к общей мощности трансформатора? Не углубляясь глубоко в теорию, так как там очень много зависящих друг от друга факторов, можно поступить следующим образом;
Зная расчётный ток нагрузки, умножаем его на 1,7 (схема с кенотронами), или на 1,6 (схема с диодами), потом полученный результат умножаем на напряжение нагрузки. Это будет приблизительный результат полученной мощности, которая добавится к общей мощности трансформатора. Большой ошибки здесь не будет.
Мостовой выпрямитель.
Мостовой выпрямитель, так же как и двухполупериодный, обладает гораздо лучшими параметрами, чем однополупериодный и немного получше КПД, чем у двухполупериодного. Поэтому это наиболее распространённая схема.
Достоинства выпрямителя;
Среднее значение тока через вентиль почти в два раза меньше тока нагрузки. Уровень пульсаций у этой схемы в 2 раза меньше по сравнению с однополупериодной схемой выпрямления. Емкость конденсатора при одинаковом с однополупериодной схемой коэффициенте пульсаций, может быть в 2 раза меньше. Отсутствует вынужденное намагничивание сердечника. Используется всего одна вторичная обмотка.
Недостатки;
Плохое использование трансформатора, так как приходится увеличивать расчётную мощность вторичной обмотки на величину амплитудного значения напряжения вторичной обмотки, т.е. в 1,41 раз. Увеличенное число используемых вентилей (4) и необходимость их шунтирования резисторами, для выравнивания обратного напряжения на каждом их них. Хотя это уже не столь актуально при современном качестве их исполнения. Ещё в два раза большее падение напряжения, по сравнению с другими схемами, так как выпрямляемый ток проходит по двум вентилям последовательно. Но это заметно только при низком выходном напряжении и больших токах нагрузки.
Особенности схемы;
В этой схеме так же, как и в двухполупериодной, среднее значение тока через один вентиль (за период) получается почти в два раза меньше, чем ток нагрузки. То есть также можно использовать диоды с меньшим рабочим током (на 30-40%), чем ток нагрузки.
А вот действующий ток вторичной обмотки всегда будет выше, чем ток нагрузки, минимум на 1,41. Поэтому провод для вторичной обмотки в этой схеме нужно выбирать в 1,5 раза больше по току (сечение), чем ток нагрузки. Почему, потому что выпрямитель всегда будет заряжать конденсатор фильтра до амплитудного значения напряжения вторичной обмотки, и от величины этого напряжения и подсчитывается мощность. А так, как по закону сохранения энергии она никуда не пропадает, то вторичной обмотки ничего не остаётся, как постоянно восполнять эту разницу. То есть у нас например вторичная обмотка имеет напряжение 14 Вольт. На конденсаторе фильтра будет напряжение около 20-ти Вольт. Нагрузили мы её током 0,5 Ампер. Мощность получилась 10 Вт. Значит и вторичка должна отдавать 10 Вт, а при выходном напряжении 14 Вольт это будет ток примерно 0,71 Ампера, то есть больше тока нагрузки в 1,41 раз.
Вторичная обмотка в мостовой схеме выпрямителя, всегда будет отдавать энергию на заряд конденсатора до амплитудного значения напряжения, а нагрузка разряжать его. То есть это как повышающий преобразователь, где низковольтная часть — это вторичная обмотка, а высоковольтная — конденсатор фильтра. Поэтому и ток вторичной обмотки всегда будет выше тока нагрузки на эту разницу напряжений, то есть минимум в 1,41 раз.
Например нашли Вы трансформатор с выходным напряжением 24 Вольта и током нагрузки 5 Ампер (120 Вт). Собрали линейный регулируемый блок питания, подключили к нему нагрузку 12 Вольт и током потребления 5 Ампер (60 Вт). Вроде всё нормально должно быть. Погоняли с полчаса-час, запахло палёным, потрогали трансформатор — обожглись. Как так?
Давайте проверим что у нас было с трансформатором;
Ток нагрузки 5 Ампер, напряжение на конденсаторе фильтра в режиме ХХ будет 24х1,41=33,84 Вольта. Мощность потребляемая нагрузкой будет 33,84х5=169,2 Вт, притом это не зависит от выходного напряжения Вашего БП, хоть 5 Вольт, хоть 25. Остальная мощность просто потеряется на регулирующем транзисторе.
И вот оказывается, что в течении часа наш транс отдавал мощность нагрузке 170 Вт!!!, хотя его мощность 120.
Вывод; Для схемы мостового выпрямителя, сечение провода вторичной обмотки необходимо выбирать на 50% или в 1,5 раза больше планируемого тока нагрузки для обеспечения нормальных условий работы трансформатора, или же выбирать трансформатор для своей конструкции с током вторичной обмотки выше планируемого на такую же величину, так как ток нагрузки на трансформаторах указан для активной нагрузки.
Ну и соответственно мощность вторичной обмотки подсчитывается так: Ток нагрузки умножаем на напряжение вторичной обмотки и полученный результат умножаем на 1,5.
Схема удвоения напряжения.
Схема удвоения напряжения, тоже довольно часто применяется на практике. Схема состоит из двух однополупериодных выпрямителей, включенных последовательно и работающих на общую нагрузку. Особенностью данной схемы является то, что в одном полупериоде от вторичной обмотки “заряжается” один конденсатор, а во втором полупериоде от той же обмотки – другой. Поскольку конденсаторы включены последовательно, то результирующее напряжение на обоих конденсаторах (на нагрузке) в два раза выше, чем можно получить от той же вторичной обмотки в схеме с однополупериодным выпрямителем. То есть максимальное выходное напряжение ХХ выпрямителя равно U2 х 2,82 , почти в три раза больше напряжения вторичной обмотки.
Достоинства выпрямителя;
Вторичную обмотку трансформатора можно рассчитывать на значительно меньшее напряжение. Отсутствует вынужденное намагничивание сердечника. Используется всего одна вторичная обмотка.
Недостатки;
Большая зависимость выходного напряжения от тока нагрузки. Значительные токи через вентили выпрямителя и вторичную обмотку. Уровень пульсаций значительно выше, чем в схемах двухполупериодных выпрямителей.
Особенности схемы;
Схемы эти на практике применяются для получения высоких напряжений при малых токах нагрузки. Например вполне можно использовать такую схему для питания анодных цепей в маломощных ламповых усилителях, если нет подходящего трансформатора а перематывать лень, в предварительных каскадах мощных ламповых усилителях, сеточных цепей, и т.д.. Пульсации на нагрузке здесь такие же, как в мостовой или двухполупериодной схеме выпрямителей. Ток протекающий через вентиль соответствует току нагрузки. Обратное напряжение на вентиль равно амплитудному значению напряжения вторичной обмотки.
Действующий ток вторичной обмотки здесь больше тока нагрузки почти в три раза (2,82). Мощность вторичной обмотки подсчитывается так, ток нагрузки умножаем на 2,9 и полученный результат умножаем на напряжение вторичной обмотки. Сечение провода вторичной обмотки для этой схемы, выбирается по току в три раза больше, чем ток потребляемый нагрузкой.
Почему так, теперь Вы сами вполне сможете догадаться. Если напряжение ХХ вторичной обмотки например 10 Вольт, то при положительном полупериоде конденсатор С1 здесь зарядится до какого напряжения? Правильно, до 14,1 вольта (до амплитудного значения напряжения вторичной обмотки, которое больше действующего в 1,41 раз). При отрицательном полупериоде конденсатор С2 так же зарядится до 14,1 вольт. Какое будет итоговое напряжение на нагрузке (R), 28,2 Вольта, то есть в 2,82 раза больше напряжения вторичной обмотки. Отсюда и вторичке ничего не остаётся, как всё время компенсировать эту разницу.
Удачи Вам в конструировании!
Список литературы;
- Терентьев Б.П. «Электропитание радиоустройств» (1958).
- Белопольский И.И. «Электропитание радиоустройств» (1965).
- Рогинский В. «Электропитание радиоустройств» (1970).
Глава 2. Методики анализа и расчета выпрямителей
2.1. Анализ работы выпрямителя гармонического напряжения при нагрузке, начинающейся с емкостного элемента
Проведем анализ работы выпрямителя гармонического напряжения с нагрузкой, начинающейся с емкостного элемента, и рассмотрим процессы в многофазных схемах выпрямителей (рис. 2.1, а). Возьмем в качестве вентиля идеализированный диод с потерями, а в трансформаторе учтем только сопротивления обмоток. Примем за r сумму активных сопротивлений вентиля и обмоток трансформатора (рис. 2.1, б):
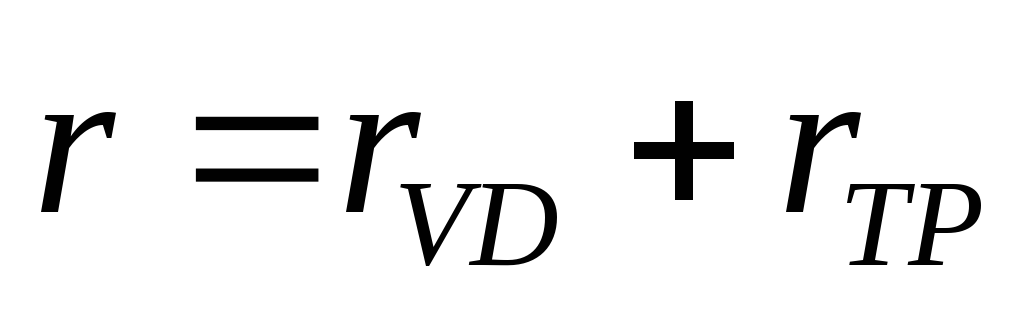 (2.1)
(2.1)
Рассмотрение
начнем с момента 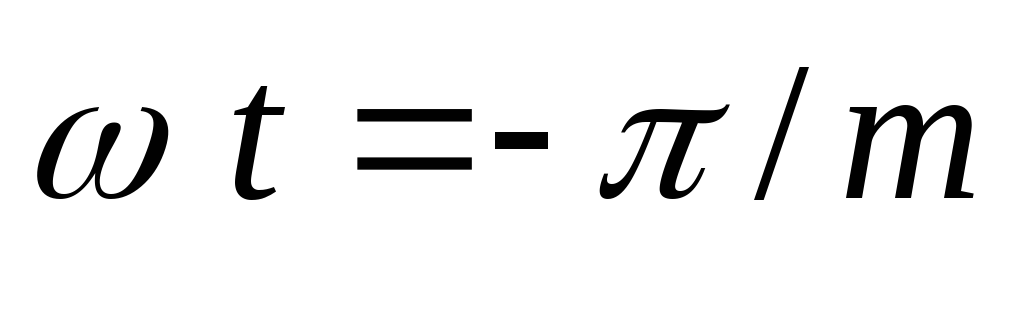 .
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При
.
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При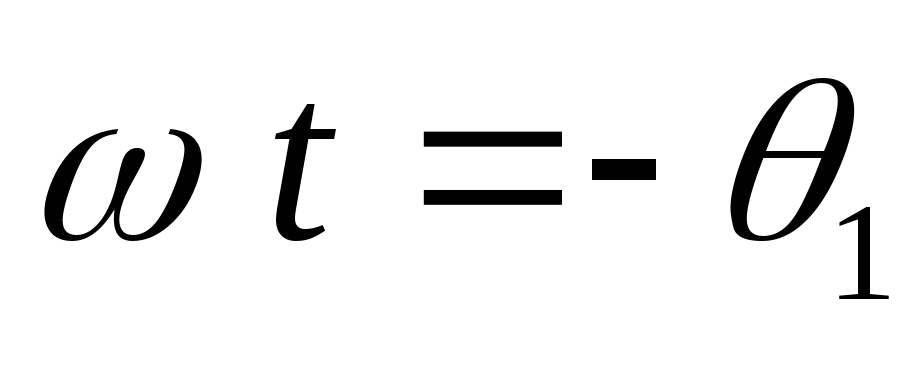 спадающее напряжение на конденсаторе
сравняется с возрастающей ЭДС первой
фазы
спадающее напряжение на конденсаторе
сравняется с возрастающей ЭДС первой
фазы ,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку.
,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку.
При зарядке
конденсатора напряжение на нем растет
и при угле 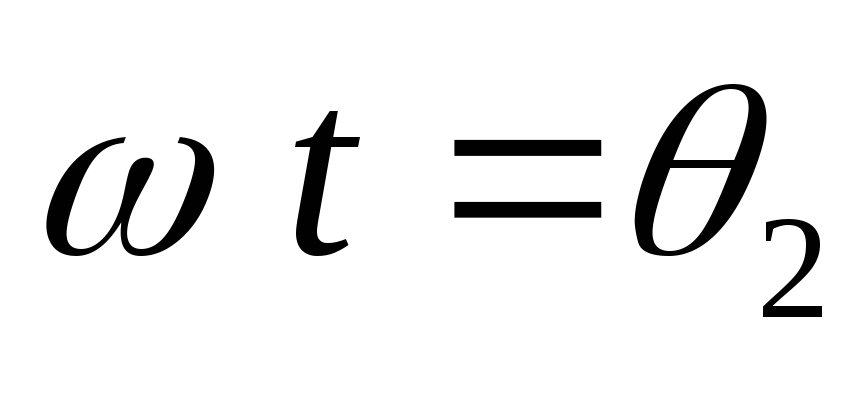 сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла
сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла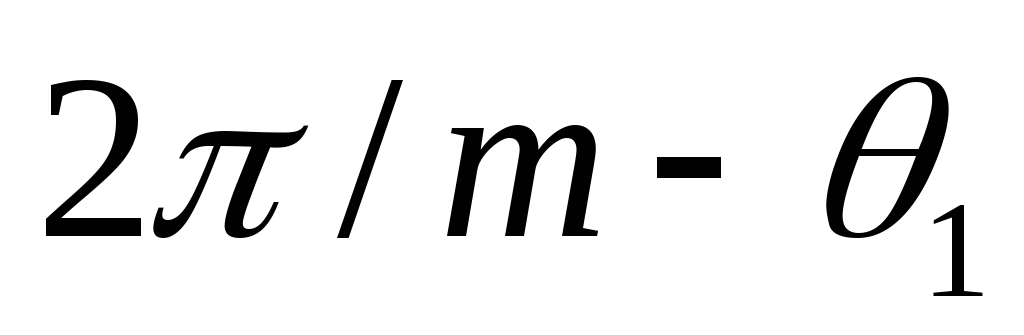 .
При угле
.
При угле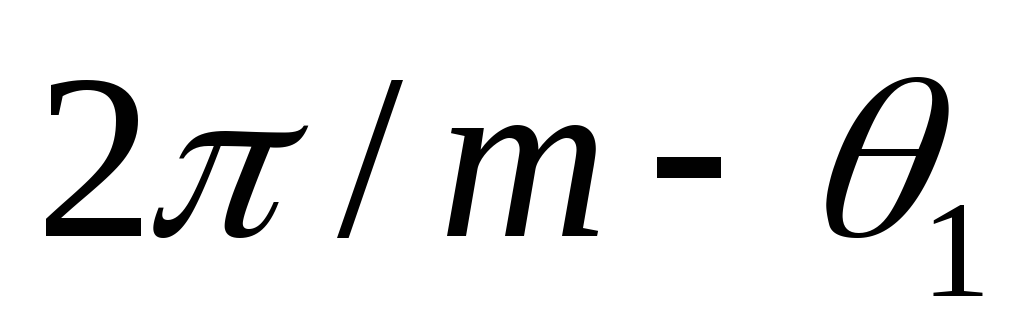 открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.
открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.
Определим ток вентиля, исходя из эквивалентной схемы открытой фазы (рис. 2.1, б). В данной схеме разность ЭДС фазы и выпрямленного напряжения получается из-за падения напряжения на сопротивлении r и, следовательно,
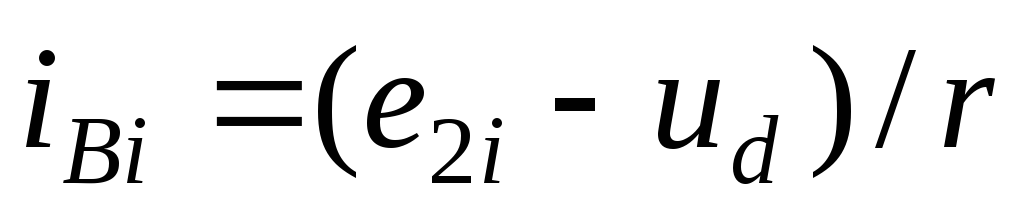 (2.2)
(2.2)
Таким образом, по
форме ток вентиля совпадает с напряжением 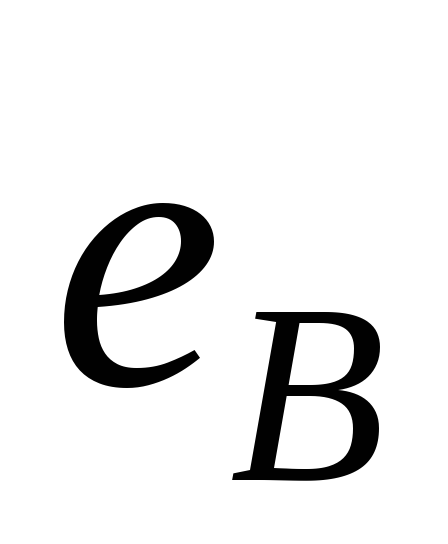 ,
равным разности ЭДС фазы и выпрямленного
напряжения (рис. 2.1, в, г).
,
равным разности ЭДС фазы и выпрямленного
напряжения (рис. 2.1, в, г).
Импульс тока
вентиля второй фазы совпадает по значению
и форме с импульсом тока первой фазы,
но запаздывает на угол 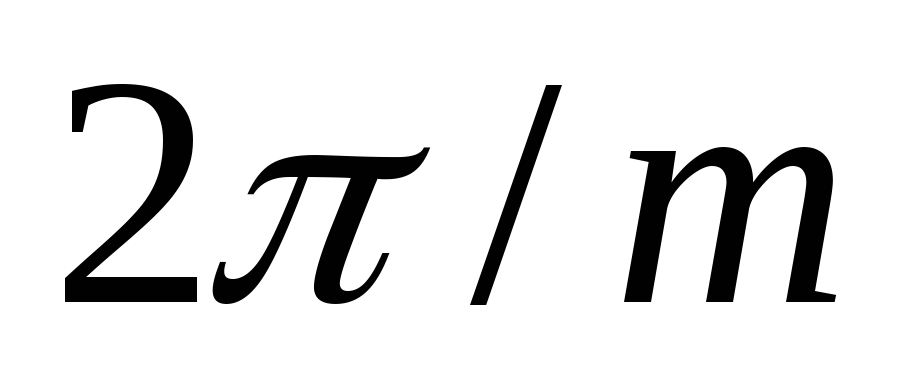 (рис. 2.1, д). Общий выпрямленный ток
(рис. 2.1, д). Общий выпрямленный ток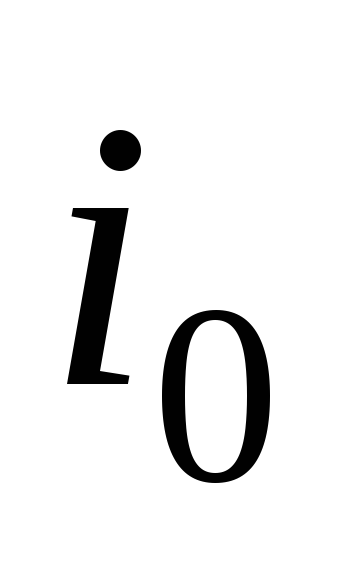 представляет собой сумму токов всех
вентилей, подходя к точкеа (рис. 2.1, а)
он делится. Часть его
представляет собой сумму токов всех
вентилей, подходя к точкеа (рис. 2.1, а)
он делится. Часть его 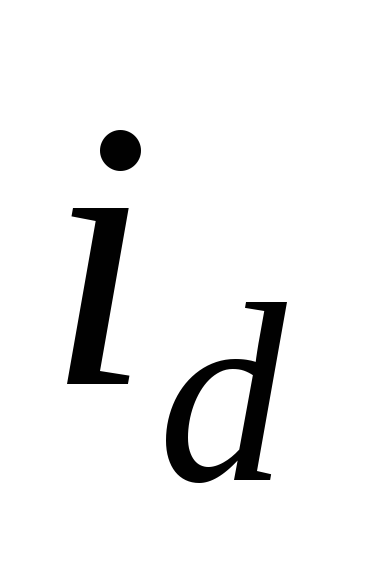 течет через нагрузку, а часть
течет через нагрузку, а часть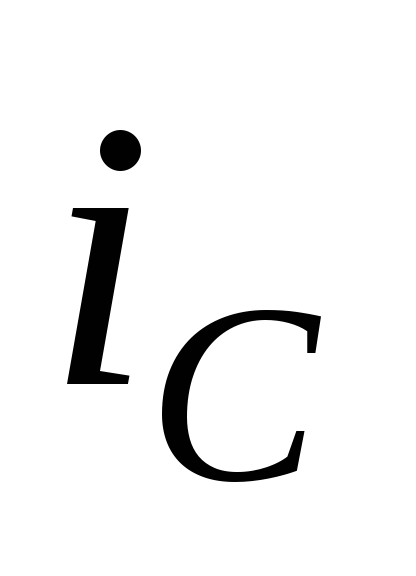 – через конденсатор. Ток
– через конденсатор. Ток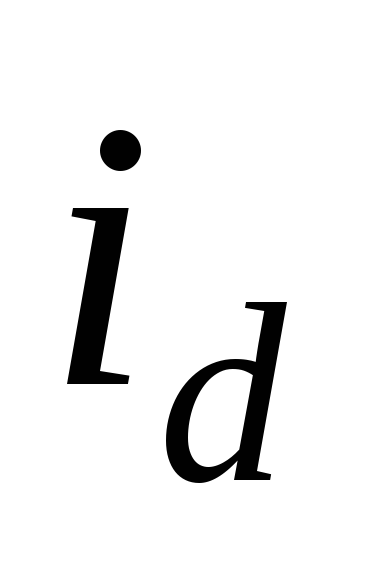 ,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
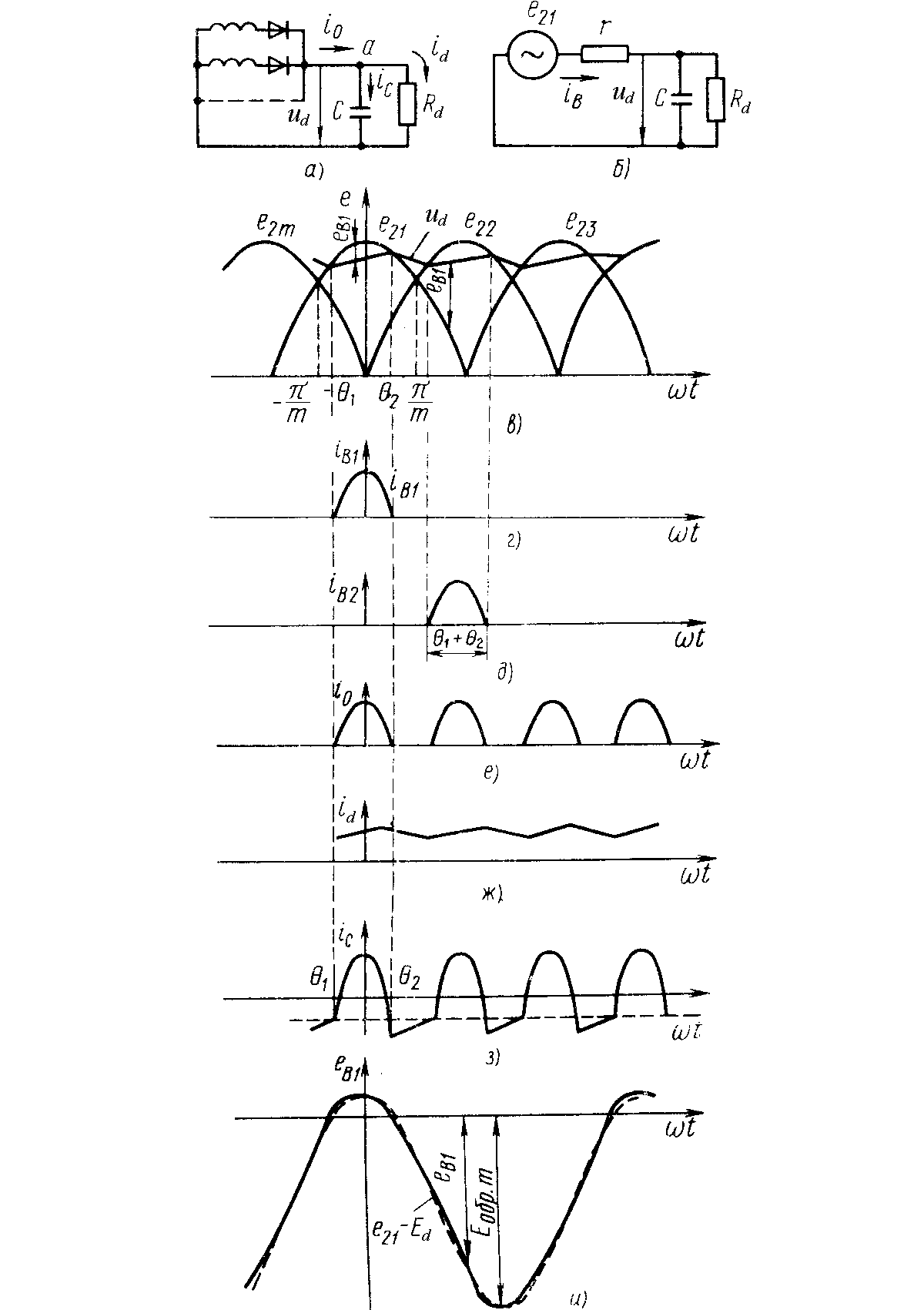
Рис. 2.1. Схемы (а, б) и диаграммы электромагнитных процессов выпрямителя гармонического напряжения с емкостным фильтром (в — и).
Напряжение на
вентиле первой фазы  меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода
меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода .
Отрицательное обратное напряжение
достигает максимума при
.
Отрицательное обратное напряжение
достигает максимума при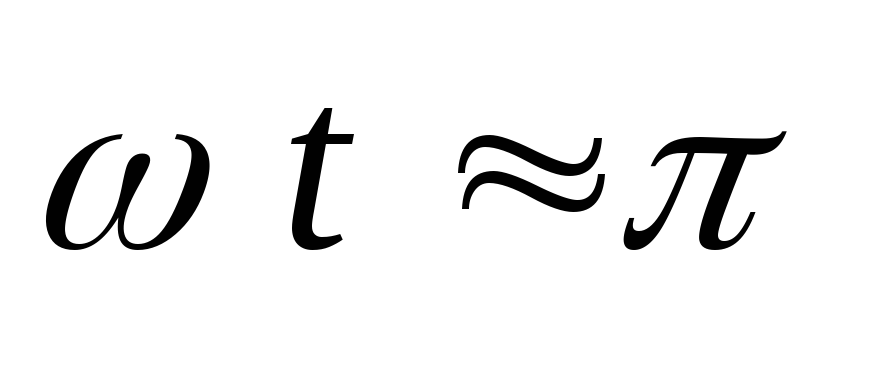 :
:
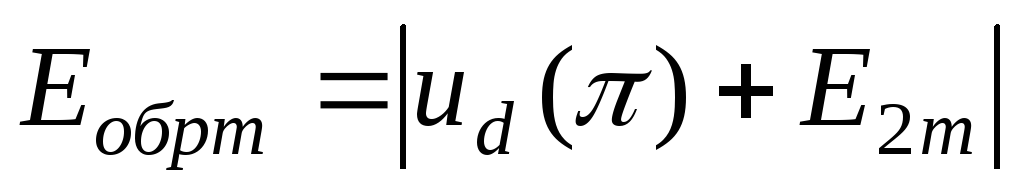 ,
(2.3)
,
(2.3)
что значительно больше выпрямленного напряжения.
Увеличение
сопротивления нагрузки 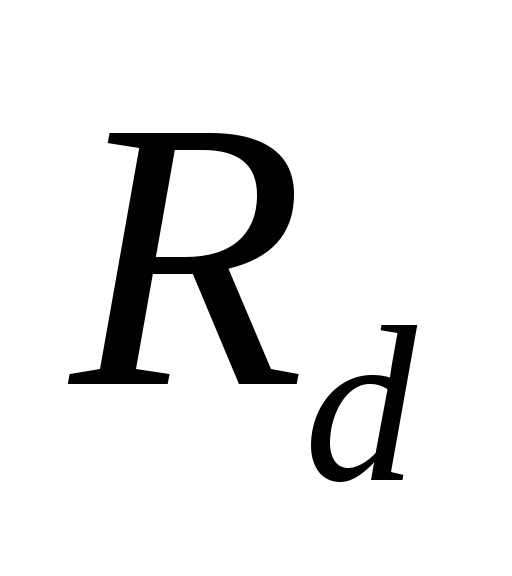 приводит к уменьшению тока нагрузки
приводит к уменьшению тока нагрузки и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол
и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол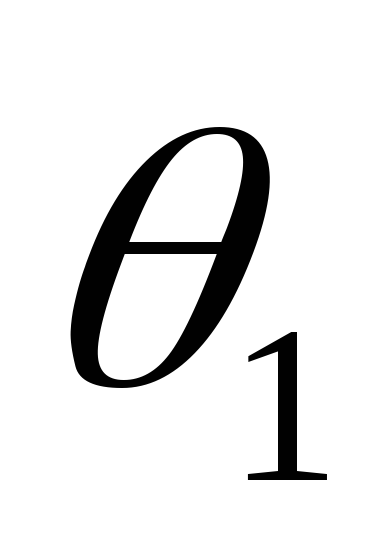 по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла
по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла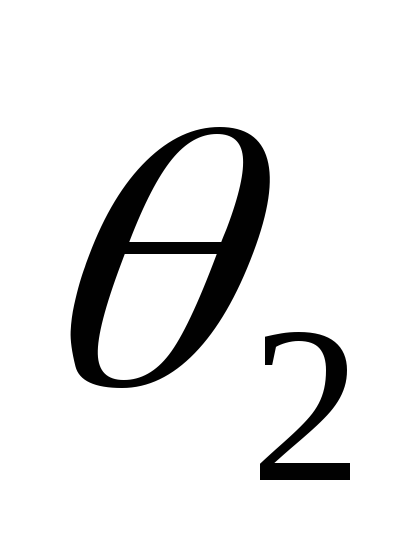 .
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от
.
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от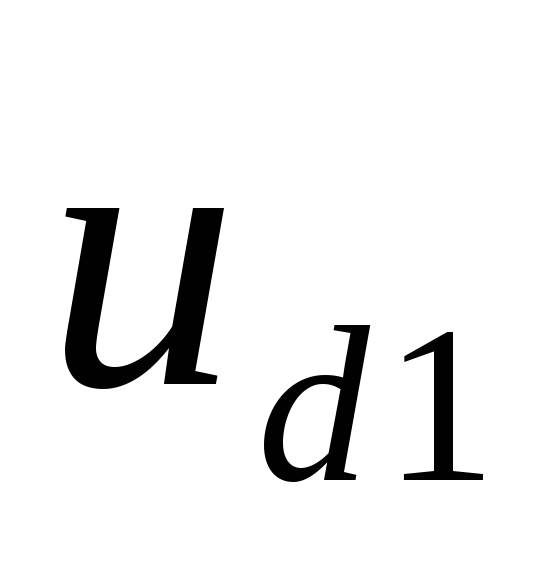 до
до и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение
и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение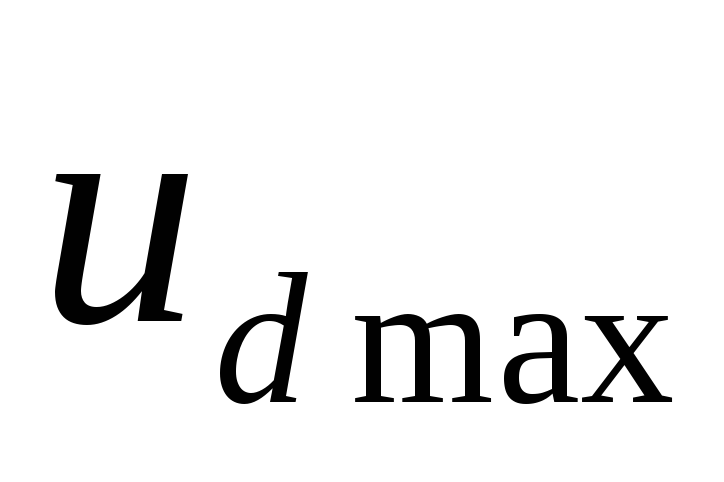 ,
равное амплитуде ЭДС
,
равное амплитуде ЭДС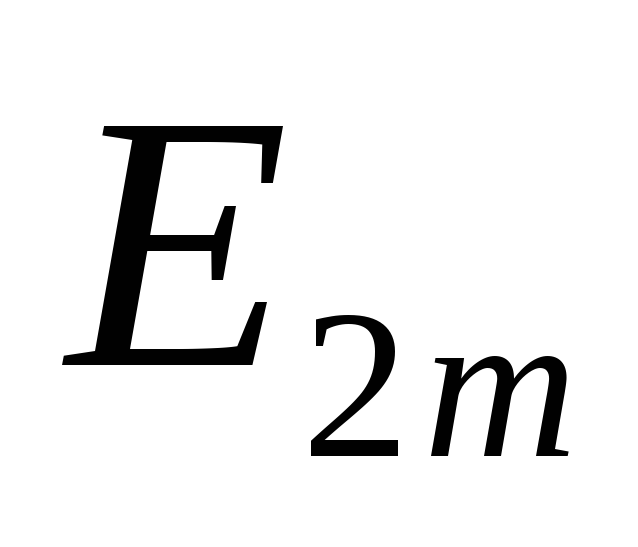 .
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
.
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
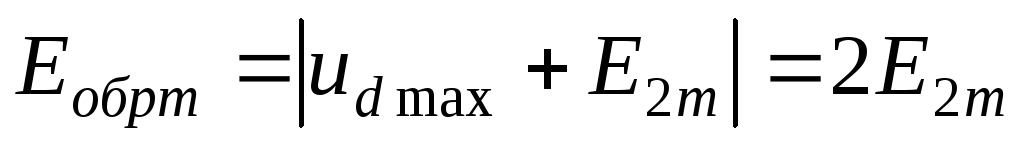 (2.4)
(2.4)
Из рассмотренного можно сделать вывод, что внешняя характеристика выпрямителя, работающего на нагрузку, начинающуюся с емкостного элемента, есть ниспадающая кривая (рис. 2.2, в), а угол отсечки зависит от тока нагрузки.
Емкость конденсатора
сказывается не только на пульсациях
выпрямленного напряжения, но и на форме
импульса тока вентиля. При очень большой
емкости конденсатора выходное напряжение
почти постоянно и импульс тока симметричен,
т.к. углы отсечки 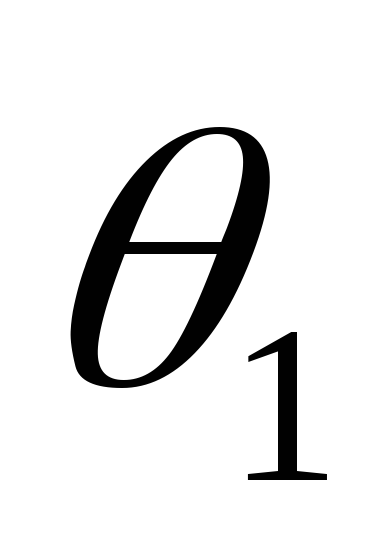 и
и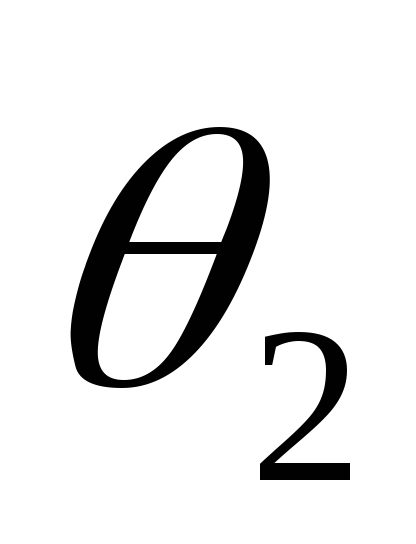 равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки
равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки становится больше угла
становится больше угла .
.
В итоге необходимо отметить следующее [6]:
1) при нагрузке, начинающейся с конденсатора, выпрямитель работает с отсечкой тока. Импульсы тока вентилей имеют длительность, меньшую T/m;
2) выпрямленное напряжение и ток нагрузки имеют пилообразную форму;
3) чем больше ток нагрузки, тем больше угол отсечки тока и тем меньше выпрямленное напряжение;
4) емкость конденсатора определяет как напряжение пульсаций, так и отклонение от косинусоидальной формы импульса тока.
С уменьшением сопротивления фазы r зарядный ток возрастает и напряжение на выходном конденсаторе нарастает круче, чем это показано на рис. 2.1, в.
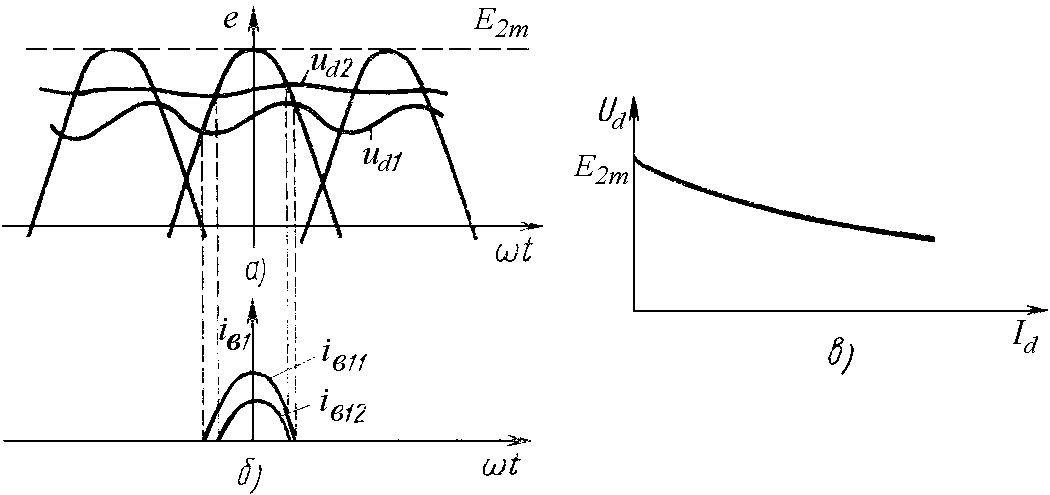
Рис.
2.2. Диаграммы электромагнитных процессов
(а, б) для нагрузок 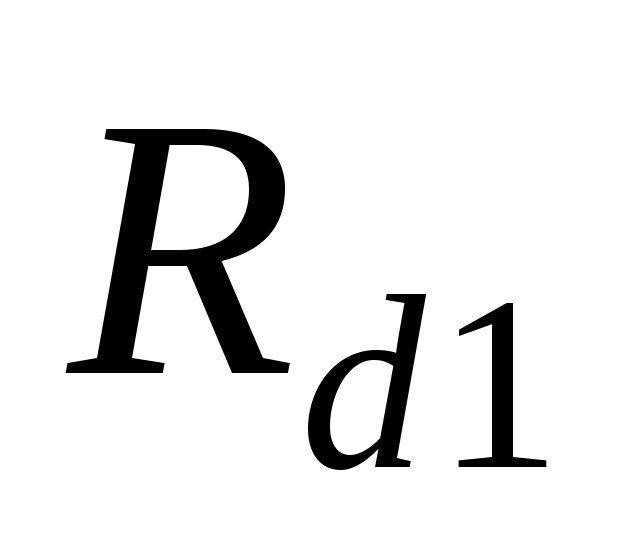 и
и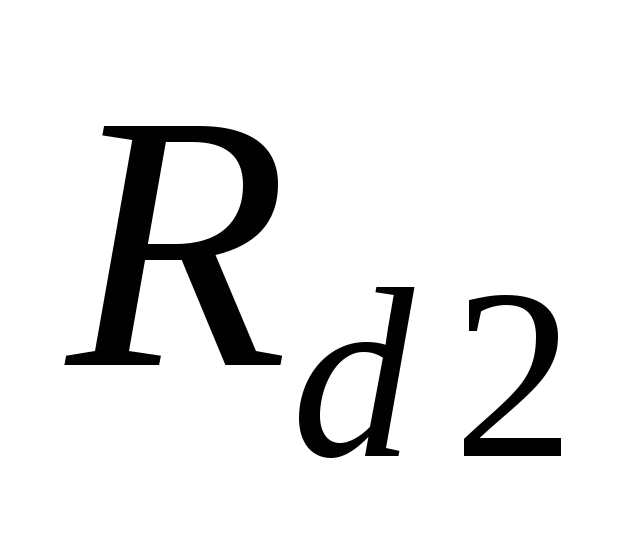 (
(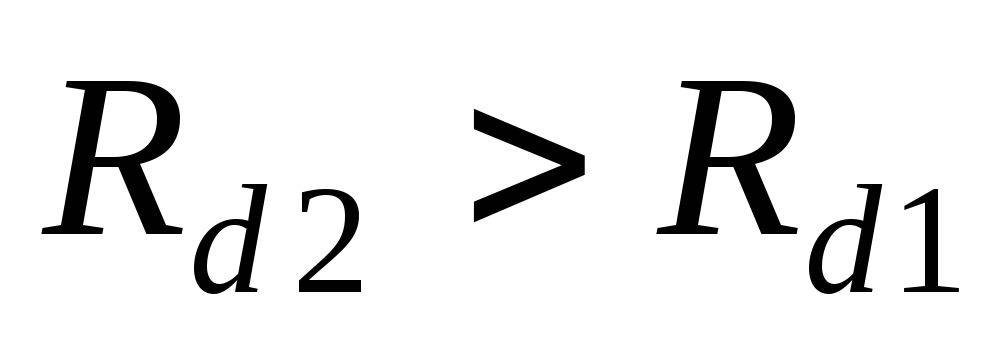 )
и внешняя характеристика выпрямителя
(в).
)
и внешняя характеристика выпрямителя
(в).
В бестрансформаторных выпрямителях сопротивление вентилей и проводов, подводящих энергию к выпрямителю, настолько мало, что напряжение на конденсаторе при его зарядке следует за ЭДС работающей фазы (рис. 2.3, а). При этом ток вентиля:
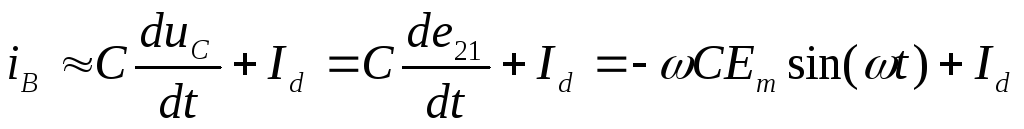 ,
(2.5)
,
(2.5)
где 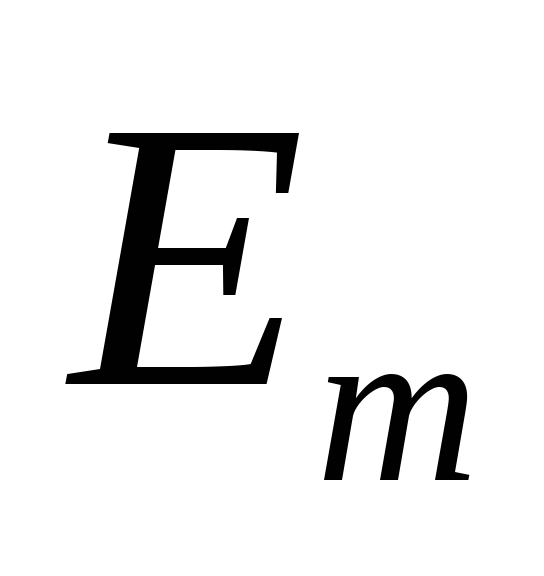 — амплитуда фазного напряжения сети,
— амплитуда фазного напряжения сети,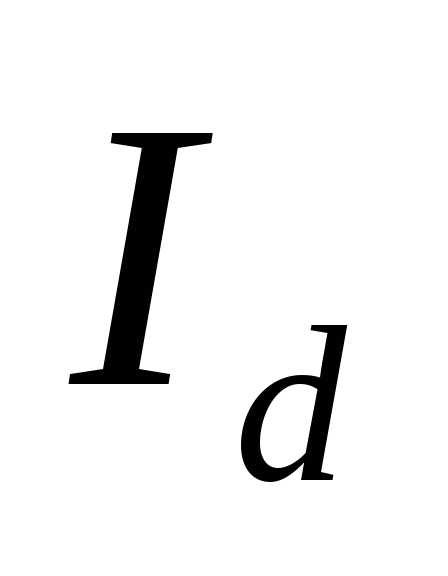 — ток нагрузки, принятый постоянным.
— ток нагрузки, принятый постоянным.
По сравнению со
случаем, когда зарядный ток ограничивался
сопротивлением зарядной цепи, импульс
тока (рис. 2.3, б) становится асимметричным.
Выходной конденсатор выпрямителя
заряжается до напряжения  от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла
от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла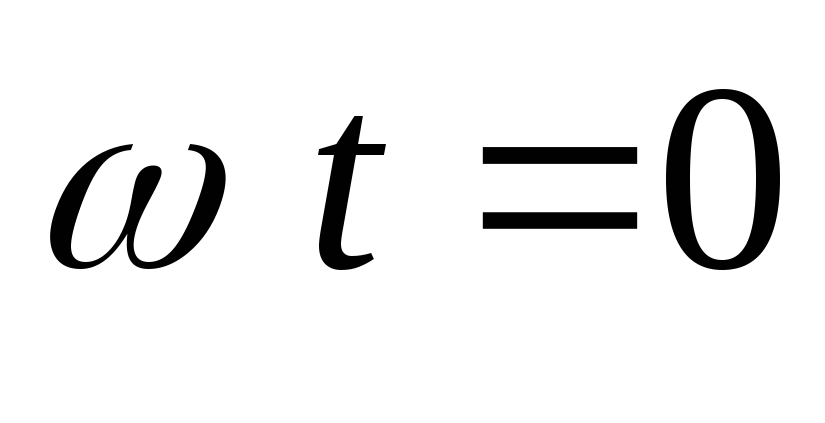 (первая фаза). При
(первая фаза). При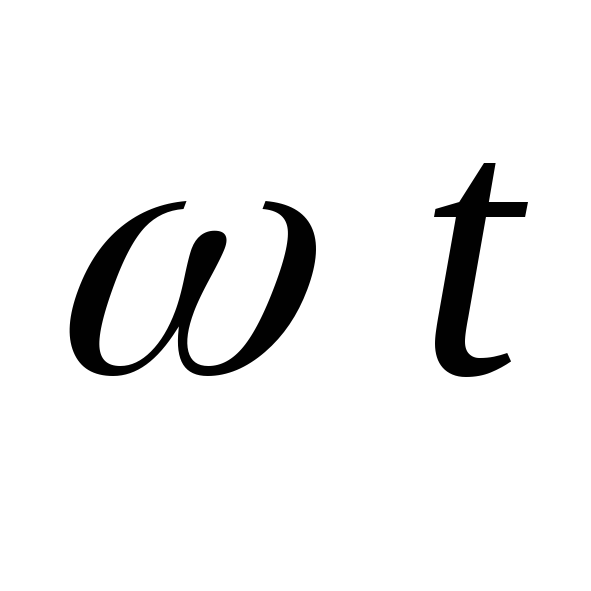 >
0 ток вентиля становится меньше тока
нагрузки и при
>
0 ток вентиля становится меньше тока
нагрузки и при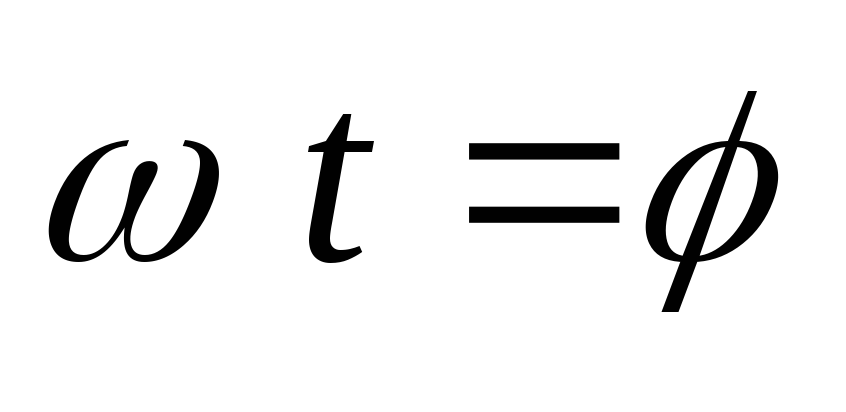 достигает нуля, вентиль закрывается.
Положив в (2.5)
достигает нуля, вентиль закрывается.
Положив в (2.5)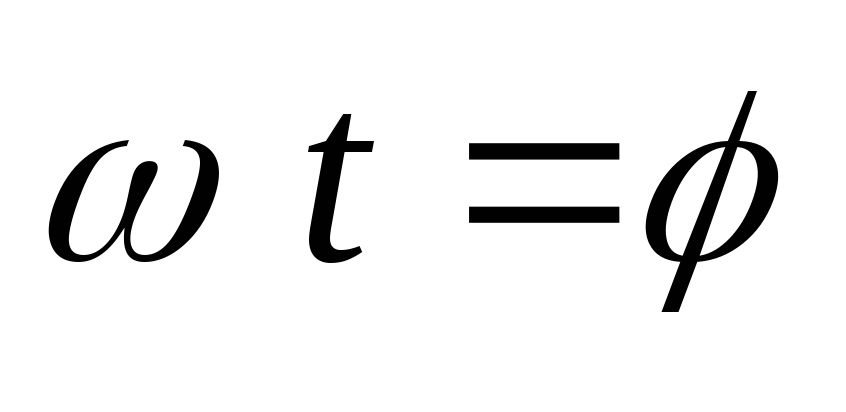 ,
получим выражение для определения угла
выключения вентилей
,
получим выражение для определения угла
выключения вентилей :
:
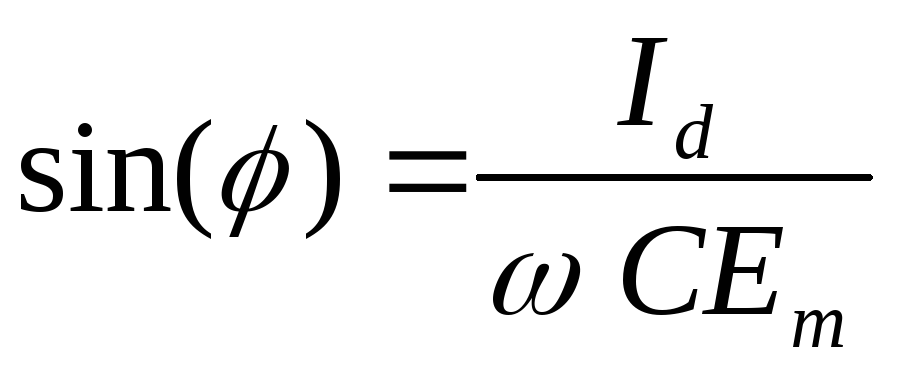 (2.6)
(2.6)
При 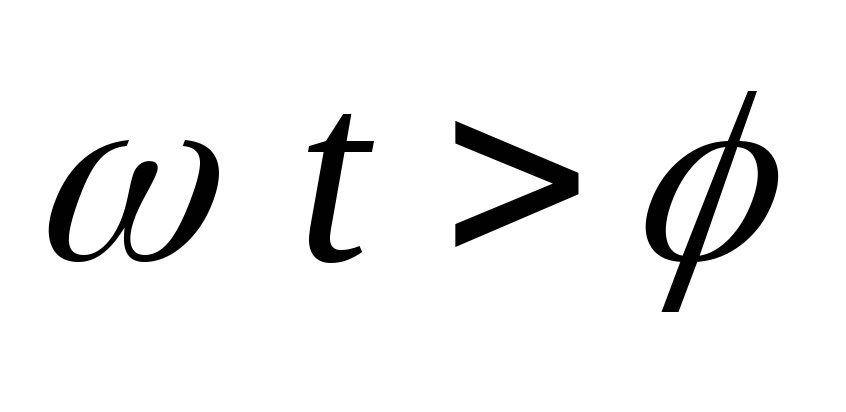 напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения
напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения  ,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы
,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы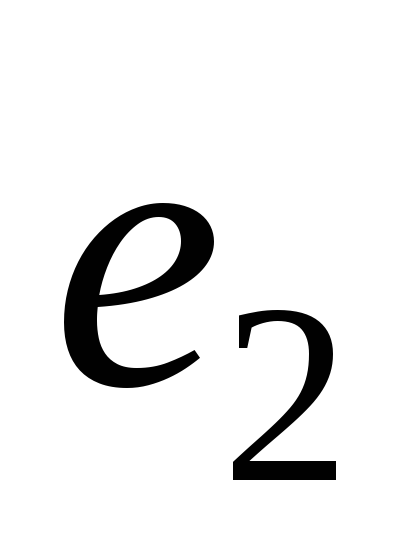 ,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
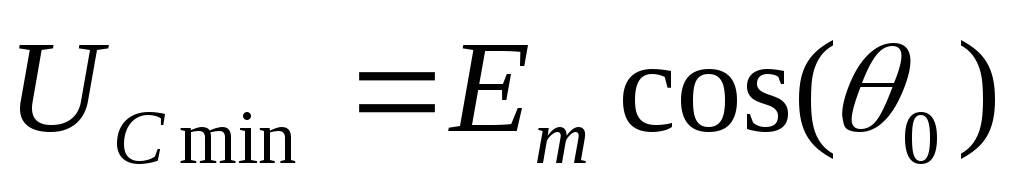 (2.7)
(2.7)
Углы  и
и связаны нелинейной зависимостью (рис.
2.3, в).
связаны нелинейной зависимостью (рис.
2.3, в).
Рис.
2.3. Диаграммы электромагнитных процессов
в бестрансформаторном выпрямителе (а,
б) и зависимость углов  и
и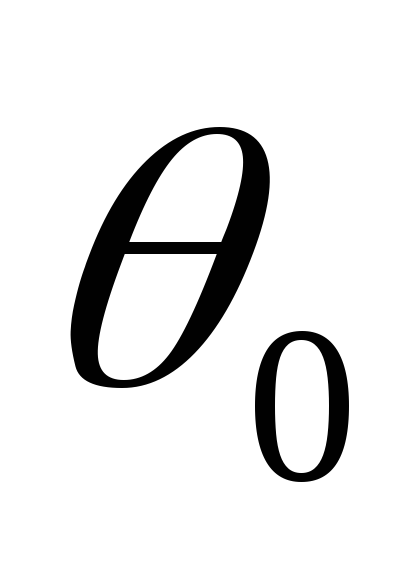 (в).
(в).
Среднее значение выпрямленного напряжения мало отличается от:
 ,
(2.8)
,
(2.8)
которое
получилось бы при линейном нарастании 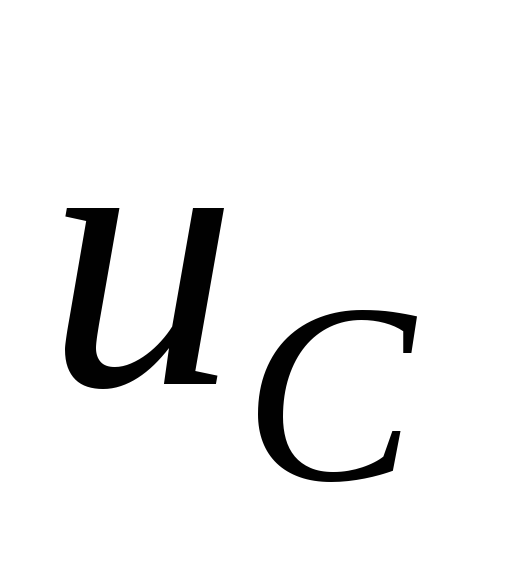 при зарядке конденсатора.
при зарядке конденсатора.
Важно отметить
заметную зависимость выходного напряжения
выпрямителя от емкости выходного
конденсатора. При увеличении емкости С спадание напряжения из-за разрядки
конденсатора замедляется и угол
открывания вентиля 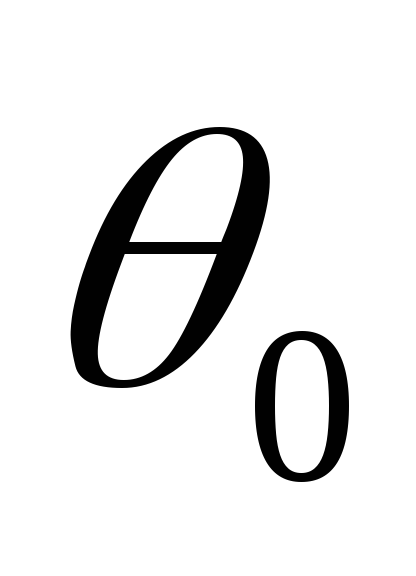 становится меньше.
становится меньше.
Таким образом, при расчете выпрямителя пользуются двумя расчетными моделями [6]. Первую расчетную модель применяют при расчетах трансформаторных выпрямителей, когда ток зарядки выходного конденсатора ограничивается активным и индуктивным сопротивлением фазы трансформатора, а также сопротивлением вентиля.
Вторая модель хорошо отражает процессы в бестрансформаторном выпрямителе. В нее закладываются малые активное и индуктивное сопротивление фазы сети и малое падение напряжения на вентилях.
Поскольку характер
выпрямителей определяется не только
сопротивлением зарядной цепи, а и
емкостью выходного конденсатора, т.е.
постоянной времени заряда, применимость
первой или второй моделей зависит от
соотношения сопротивлений фаз r и 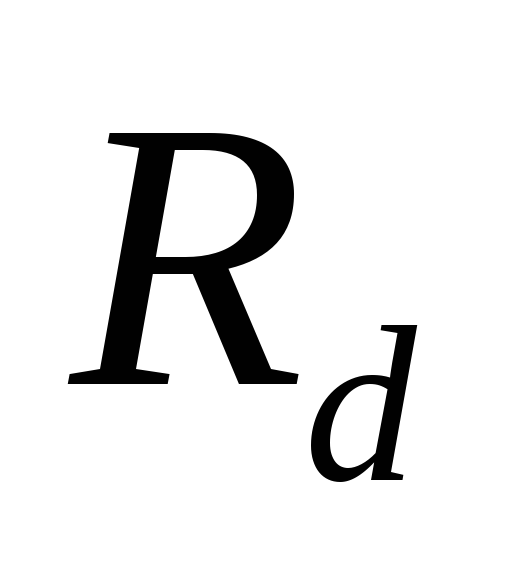 и емкости выходного конденсатораС [6].
и емкости выходного конденсатораС [6].
Пояснить методику
получения расчетных формул для первой
модели проще всего при анализе схемы
выпрямителя, приведенной на рис. 2.1, б,
где ток зарядки конденсатора ограничивается
сопротивлением r.
Так как выпрямитель всегда характеризуется
относительно небольшим напряжением
пульсаций (его значение ограничивают
допустимой реактивной мощностью
выходного конденсатора фильтра на
уровне 5-10% от 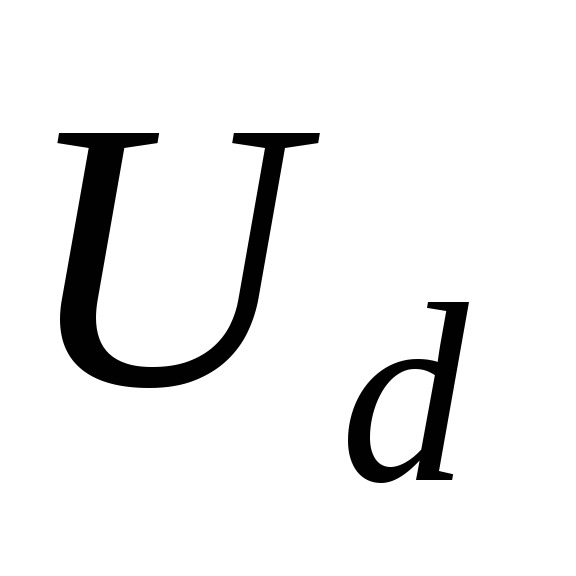 ),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки
),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки 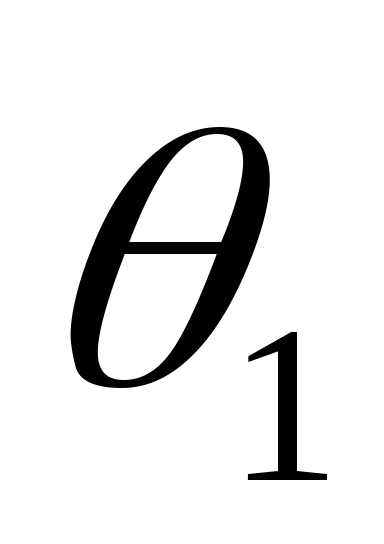 и
и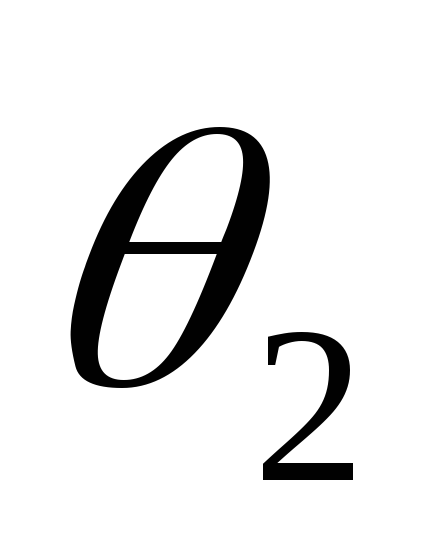 становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
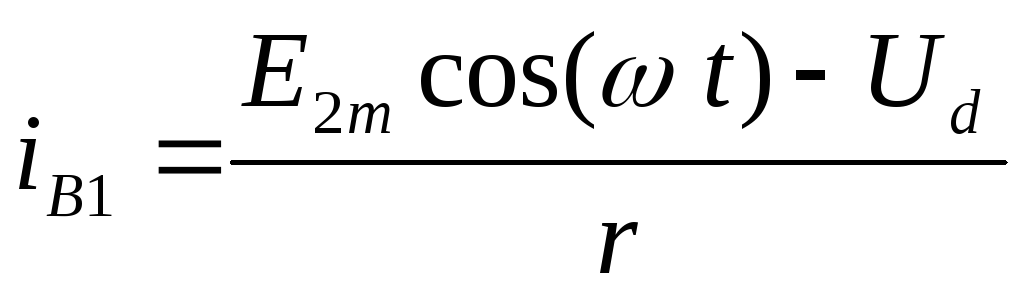 (2.9)
(2.9)
при 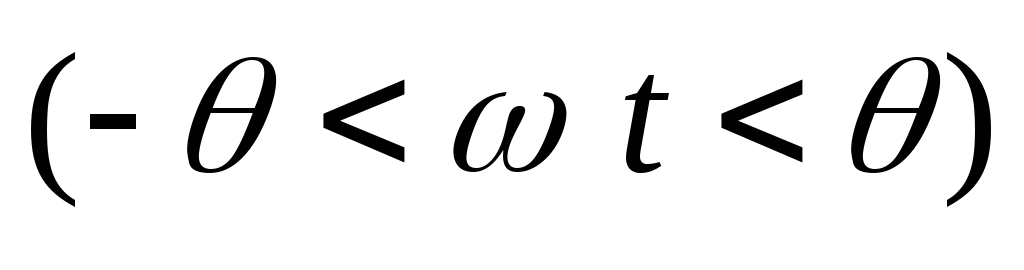 и
и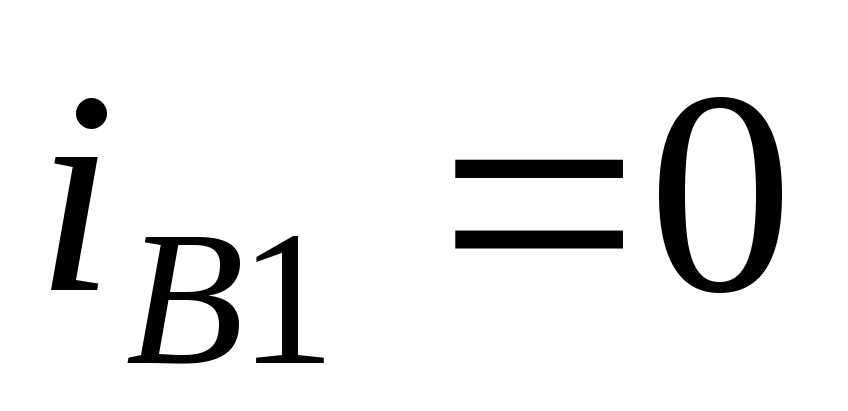 на остальной части периода.
на остальной части периода.
Постоянный ток в нагрузке выпрямителя равен сумме постоянных составляющих токов всех вентилей:
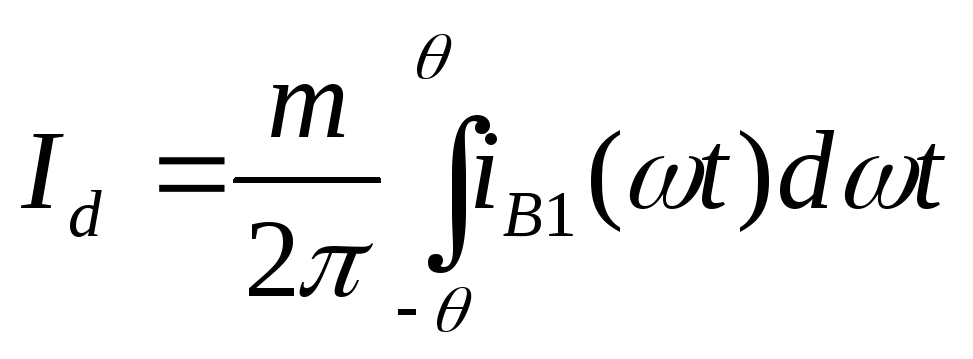 (2.10)
(2.10)
При углах 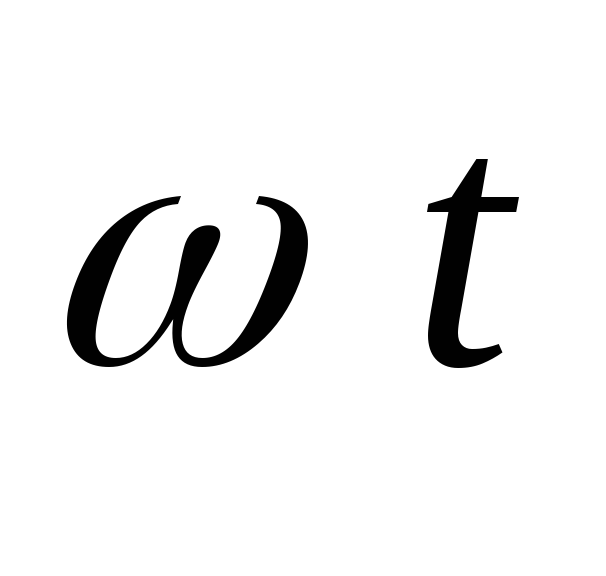 ,
равных
,
равных и,
выпрямляемое переменное напряжение
и,
выпрямляемое переменное напряжение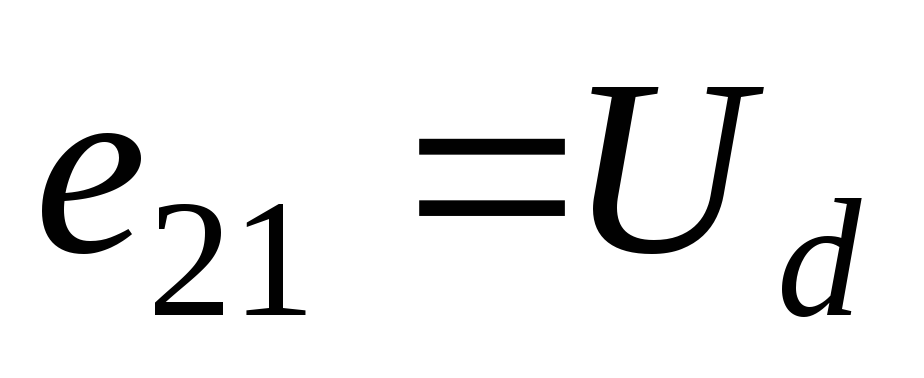 ,
что позволяет записать:
,
что позволяет записать:
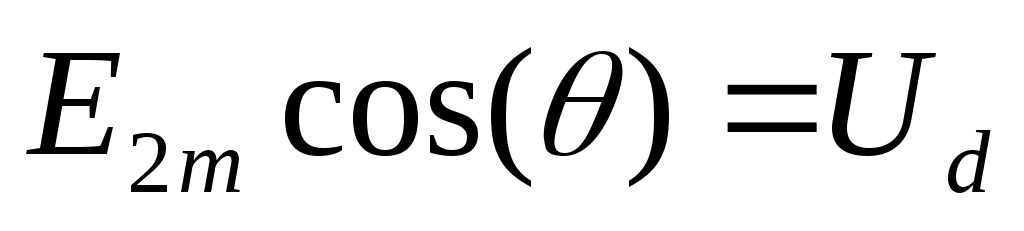 (2.11)
(2.11)
Следует отметить,
что в схеме Ларионова используется не
фазное напряжение, а линейное, поэтому
амплитудное напряжение фазы на вторичной
обмотке трансформатора будет в  раз меньше
раз меньше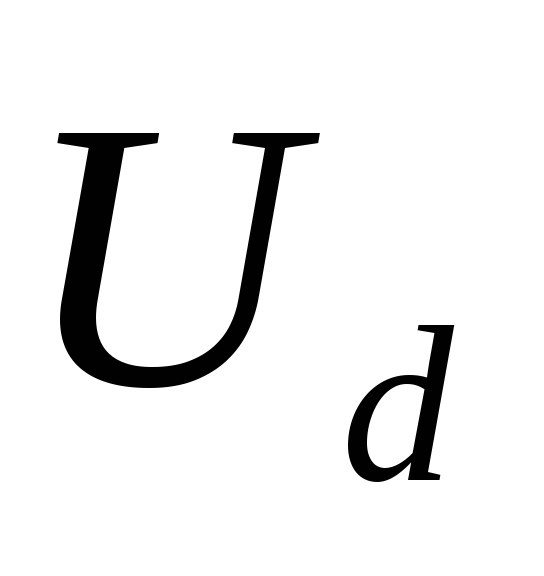 .
Максимум напряжения будет здесь не при
.
Максимум напряжения будет здесь не при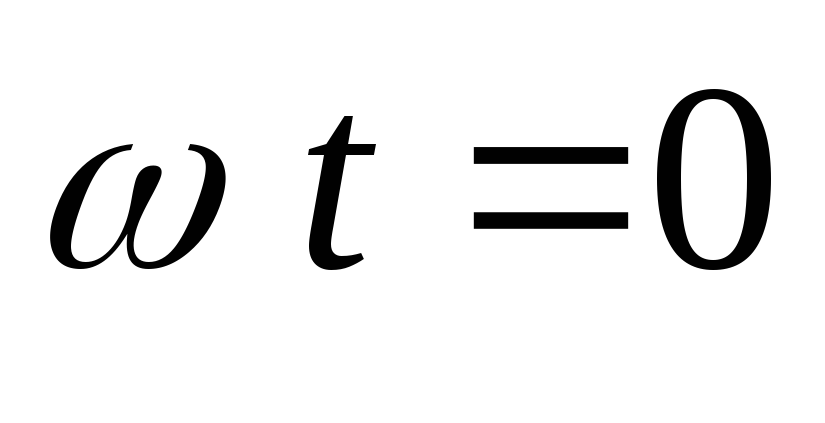 ,
а при
,
а при .
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
.
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
Произведя интегрирование (2.10), придем к выражению:
 ,
(2.12)
,
(2.12)
связывающему
параметр режима работы выпрямителя  с выходным выпрямленным напряжением
с выходным выпрямленным напряжением и током нагрузки
и током нагрузки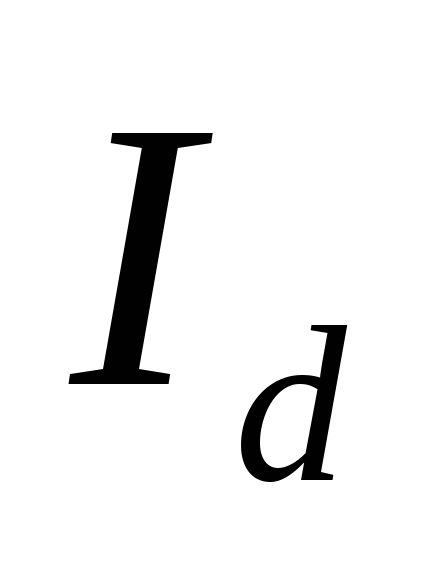 .
Обычно его записывают в несколько ином
виде [6 — 8]:
.
Обычно его записывают в несколько ином
виде [6 — 8]:
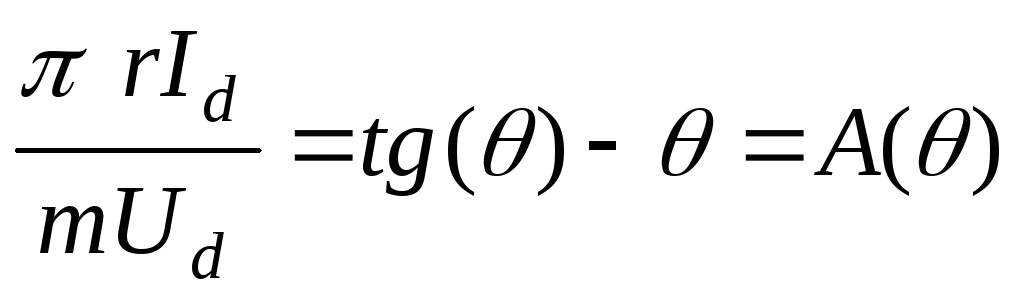 или
или 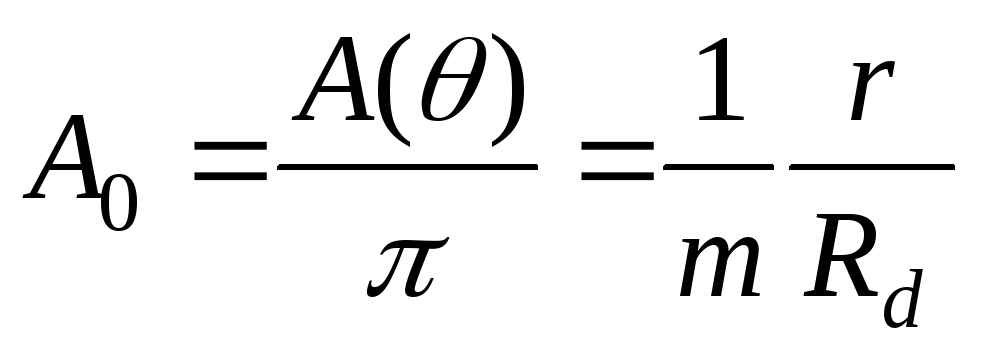 . (2.13)
. (2.13)
В этом выражении
правая часть является однозначной
функцией угла
отсечки  .
.
Соотношение (2.13)
позволяет по выходным данным выпрямителя
(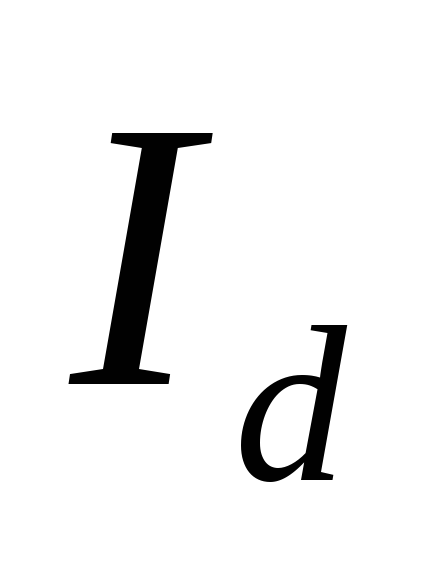 ,
,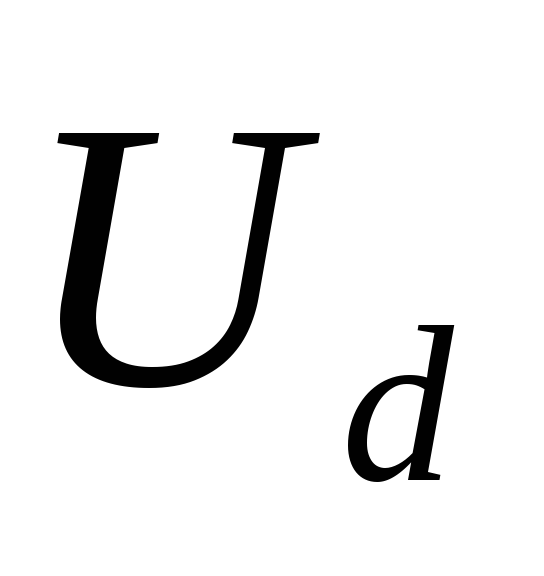 )
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки
)
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки  .
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
.
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
Действующее значение ЭДС вторичной обмотки, согласно (2.11) ,
 (2.14)
(2.14)
Действующее значение тока найдем по (2.9):
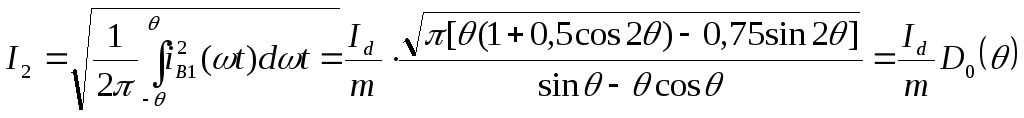 (2.15)
(2.15)
где
функция угла отсечки 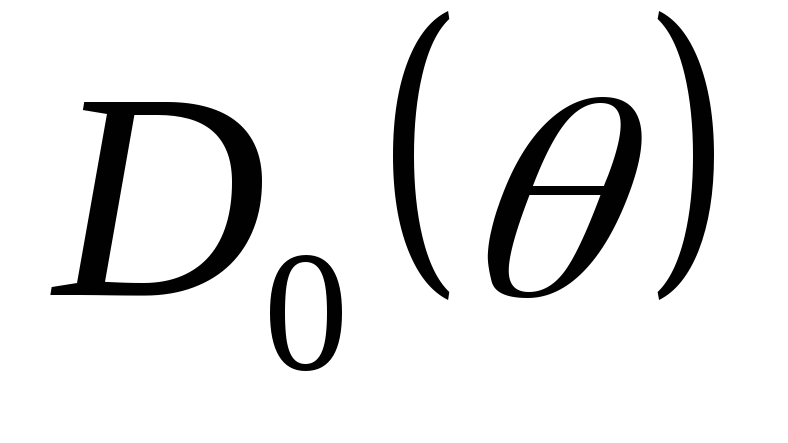 характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
Следует отметить,
что имеется разница в схемах между
действующим значением тока во вторичной
обмотке трансформатора  и током вентиля
и током вентиля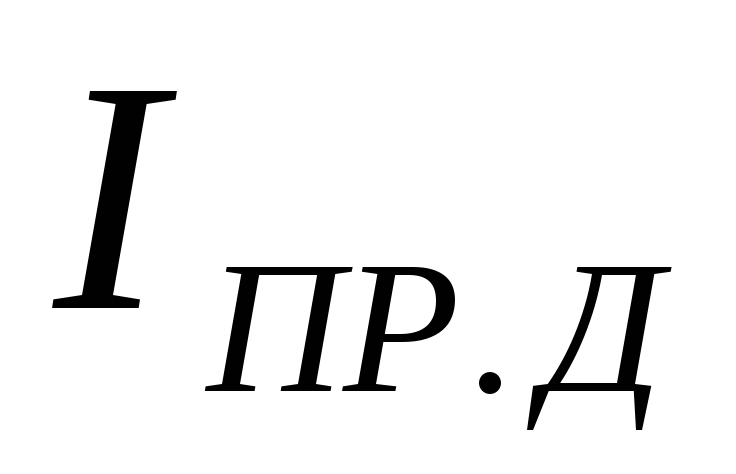 .
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
.
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
Максимального
значения ток вентиля достигает при 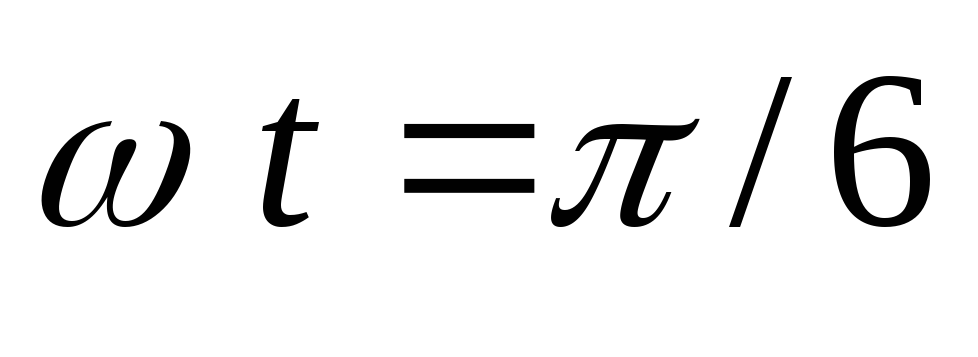 в схеме Ларионова и при
в схеме Ларионова и при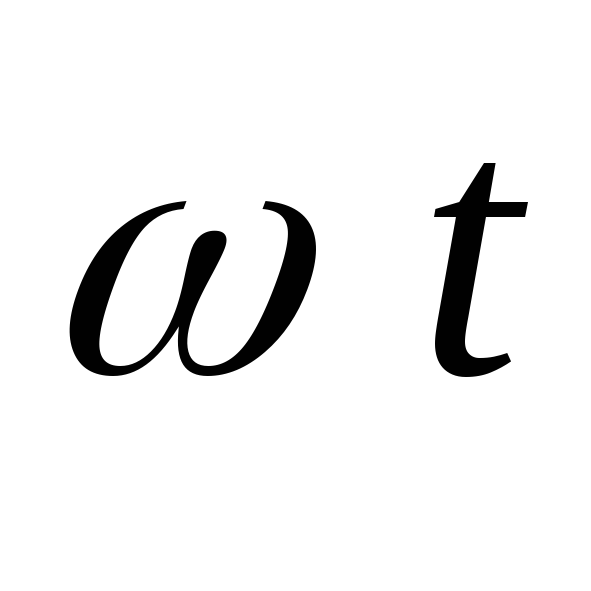 = 0 во всех остальных схемах:
= 0 во всех остальных схемах:
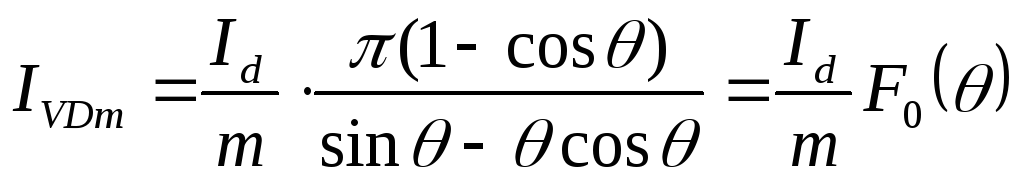 (2.16)
(2.16)
где 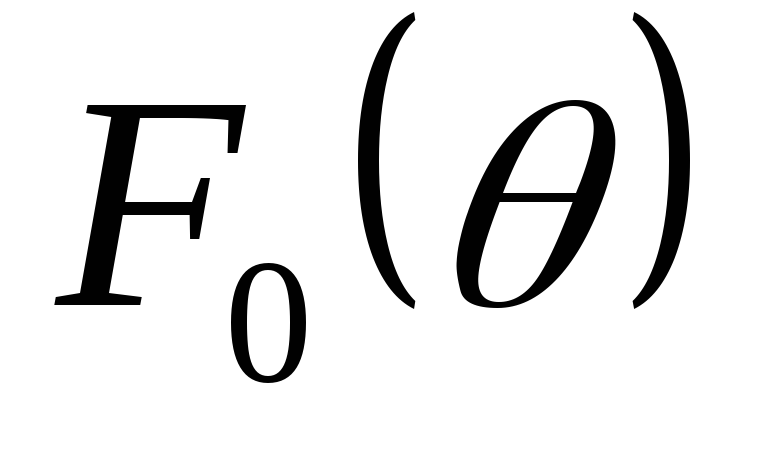 —
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
—
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
Трудность возникает
при расчете коэффициента пульсаций
выпрямителей, поскольку, положив 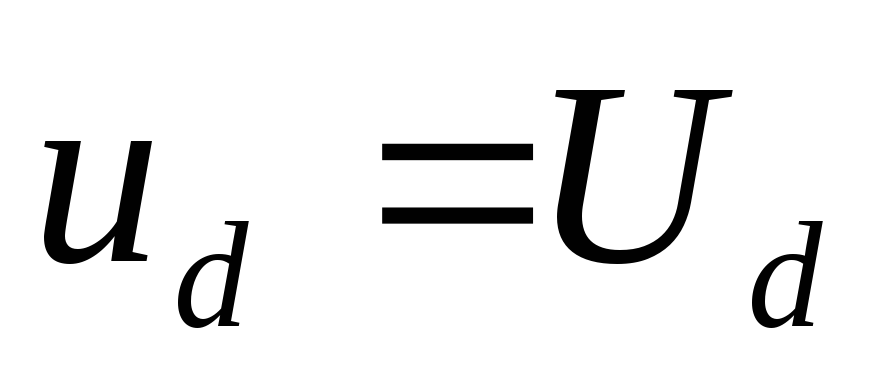 ,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
Таким образом,
общий ток всех вентилей представляет
собой совокупность импульсов тока,
определяемых (2.9) и следующих друг за
другом с интервалом 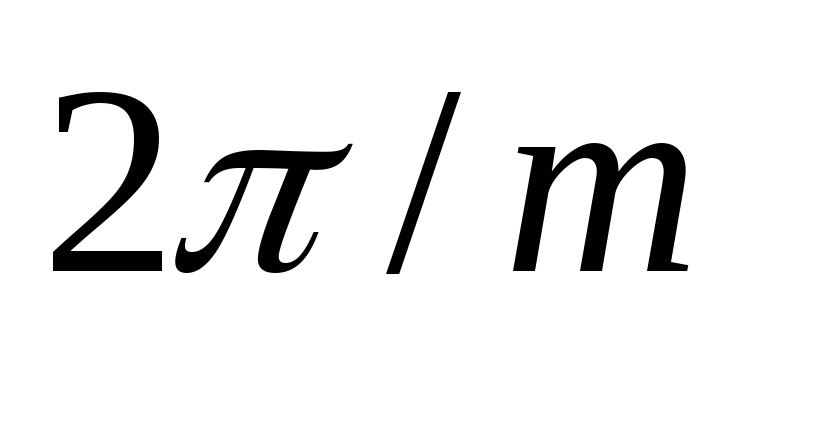 .
Амплитуда первой гармоники тока:
.
Амплитуда первой гармоники тока:
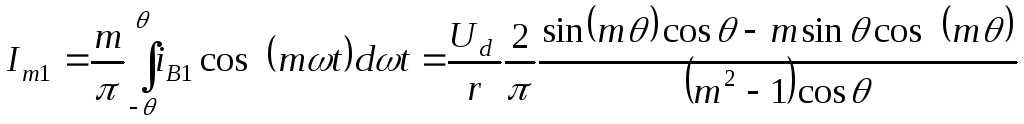 (2.17)
(2.17)
Амплитуда первой гармоники напряжения:
 (2.18)
(2.18)
Коэффициент пульсаций по первой гармонике:
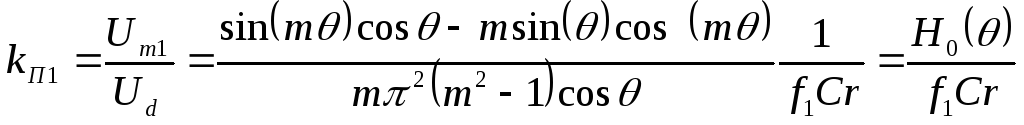 (2.19)
(2.19)
где 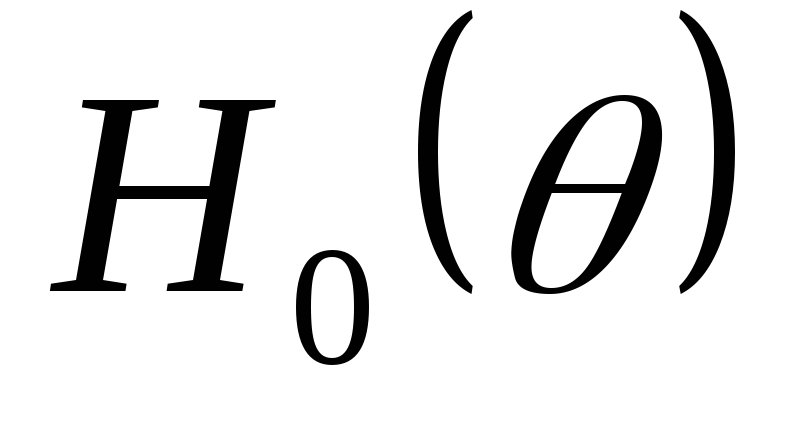 —
функция угла отсечки и числа фаз
выпрямителя.
—
функция угла отсечки и числа фаз
выпрямителя.
Данный
метод расчета из-за приближения 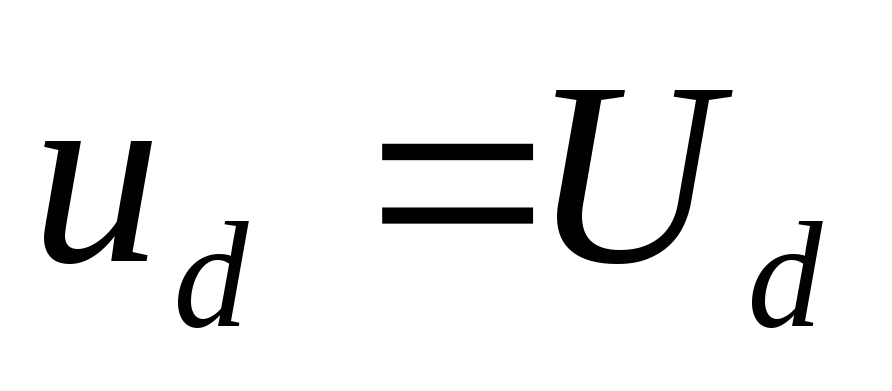 достаточно точен лишь при малых значениях
коэффициента пульсаций (
достаточно точен лишь при малых значениях
коэффициента пульсаций (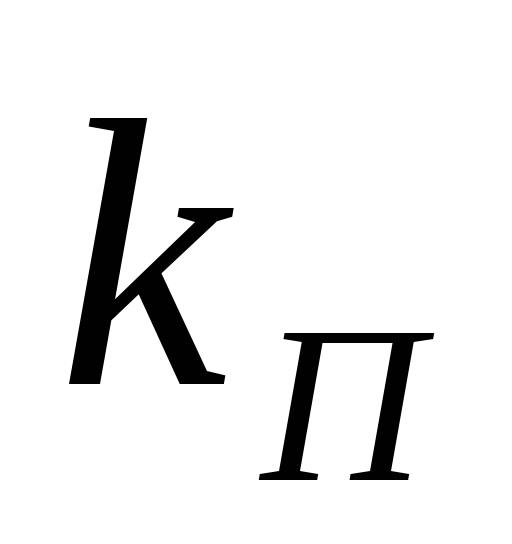 <0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что
<0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что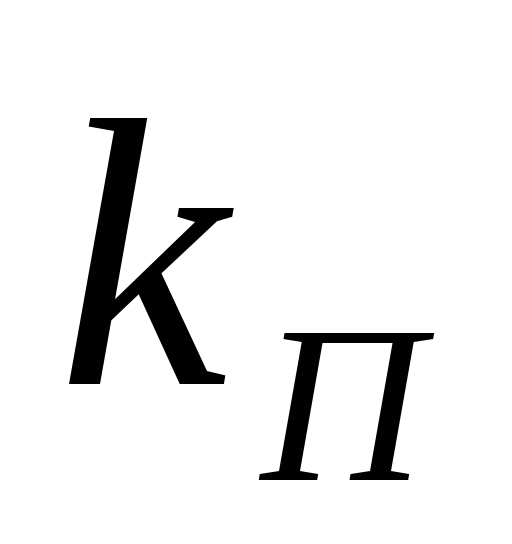 >0,12,
то точность будет ниже требуемой (
>0,12,
то точность будет ниже требуемой ( )
и возникнет необходимость изменения
расчетной модели.
)
и возникнет необходимость изменения
расчетной модели.
Самым простым
способом достижения требуемой точности
расчета является увеличение емкости
выходного конденсатора выпрямителя до
значения, которое обеспечивает выполнение
условия 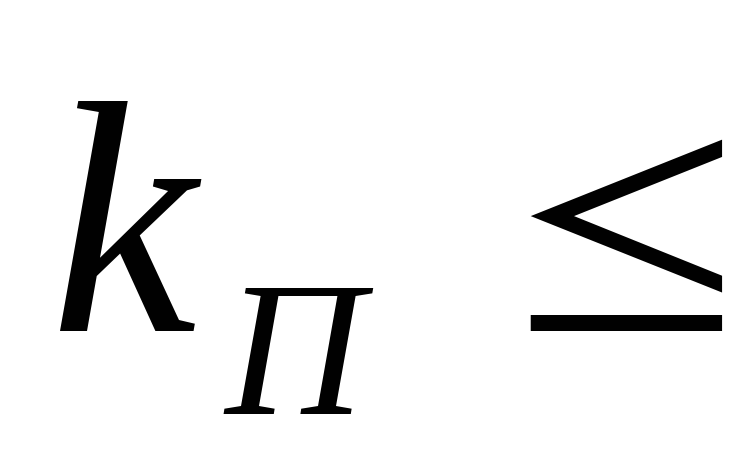 0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При
0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При 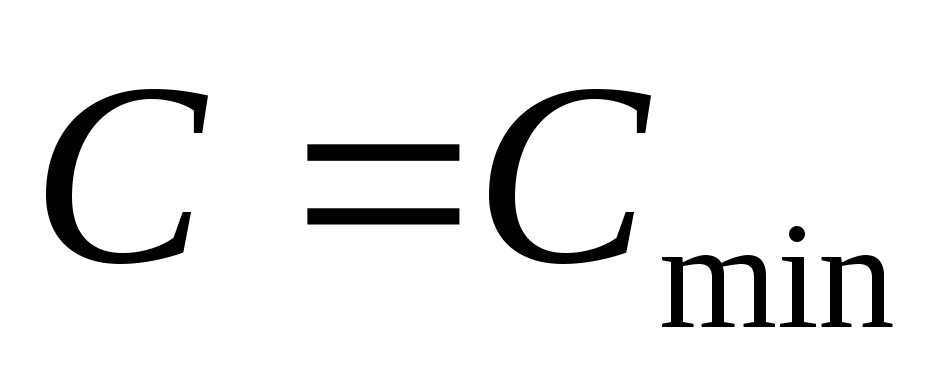 коэффициент пульсаций
коэффициент пульсаций = 0,1.
= 0,1.
Недостатком
использования формулы (2.19) является то,
что о выполнении или нарушении условия
малости пульсаций узнают только в конце
расчета, когда определен угол отсечки  и найдена функция
и найдена функция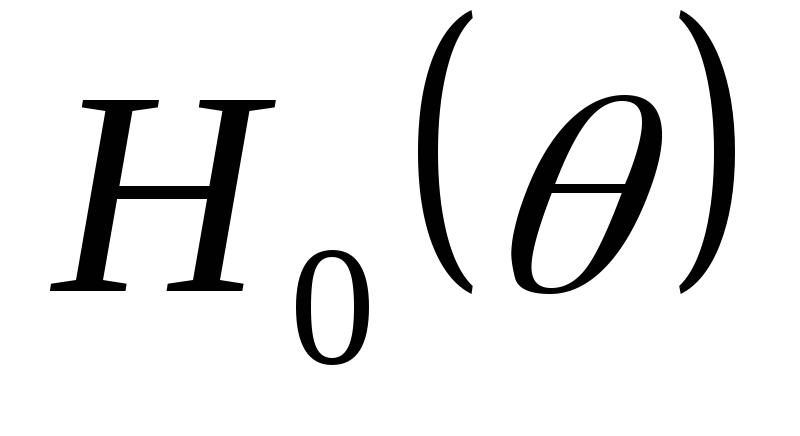 .
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость
.
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость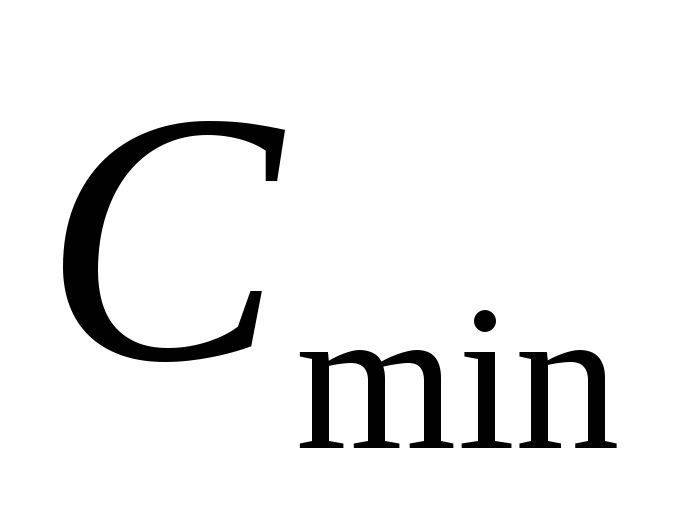 до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
Прийти к такому
соотношения можно представив зависимость  в приближенном виде. Так, для двухфазного
выпрямителя
в приближенном виде. Так, для двухфазного
выпрямителя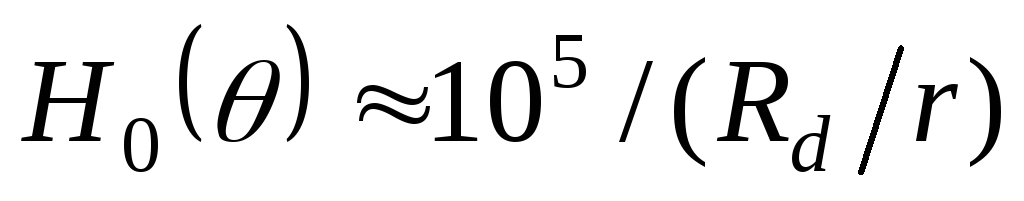 .
Подставив это приближение в (2.19), при
.
Подставив это приближение в (2.19), при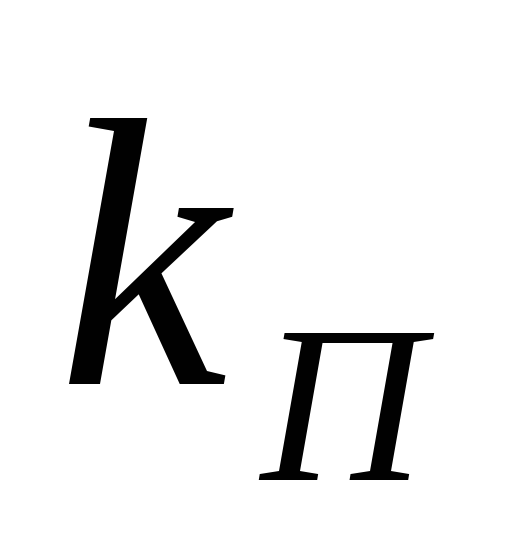 = 0,1 получим:
= 0,1 получим:
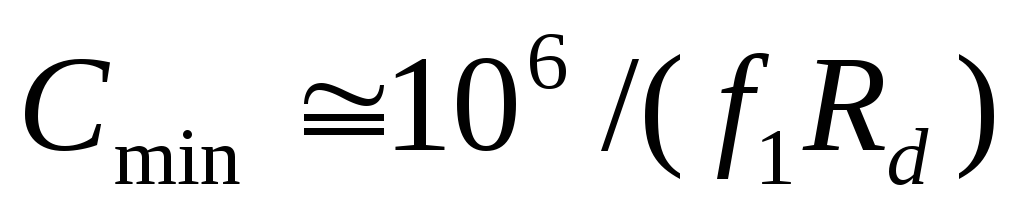 ,
(2.20)
,
(2.20)
где 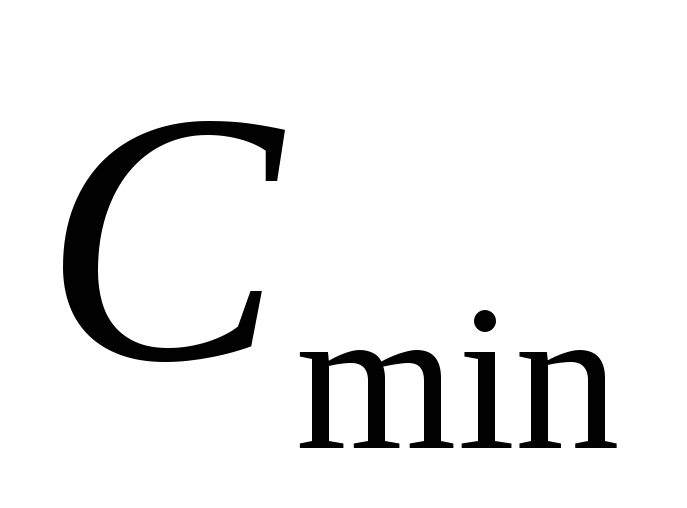 —
в мкФ.
—
в мкФ.
Таким образом, данный метод расчета выпрямителя заключается в проверке условия (2.20) с последующим определением режима работы по выражению (2.13) и нахождения расчетных показателей по формулам (2.14), (2.15), (2.16), (2.19).
Как было показано
ранее, выбранная модель (рис. 2.1, б)
достаточно проста, однако расчеты по
полученным на ее основе формулам дают
во многих случаях неплохую точность.
Вместе с тем в выпрямителях на относительно
высокие напряжения заметное влияние
на выходные показатели оказывает
индуктивность рассеяния трансформатора.
При ее учете придем к расчетной модели,
приведенной на рис. 2.4, а. Импульс тока
вентиля в такой модели заметно отличается
от косинусоидального (рис. 2.4, б) и имеет
длительность, большую  .
.
Проведя анализ
подобный ранее изложенному, получим
зависимости коэффициентов 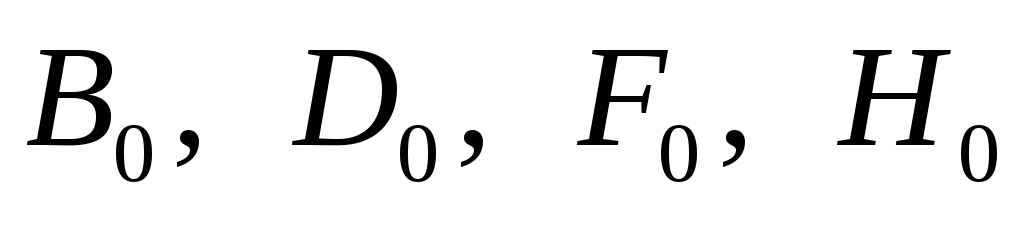 не только от угла
не только от угла ,
но и от относительного реактивного
сопротивления фазыx.
,
но и от относительного реактивного
сопротивления фазыx.
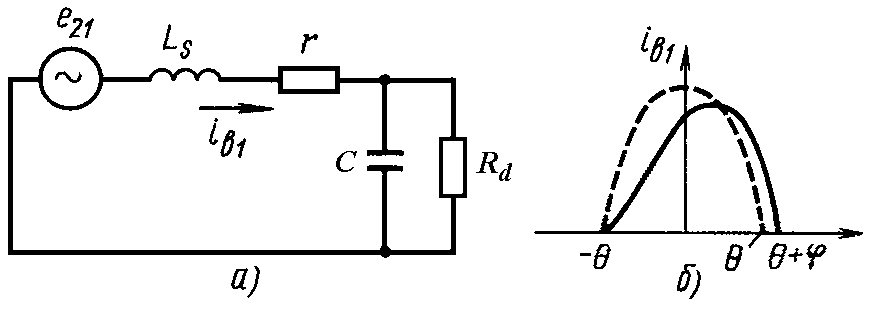
Рис. 2.4. Расчетная модель выпрямителя с учтенной индуктивностью
рассеяния (а) и кривые импульса тока вентиля в исходной и данной моделях (б).
Также может быть
определен тангенс угла  ,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
 (2.21)
(2.21)
Найденные ранее
выражения для коэффициентов 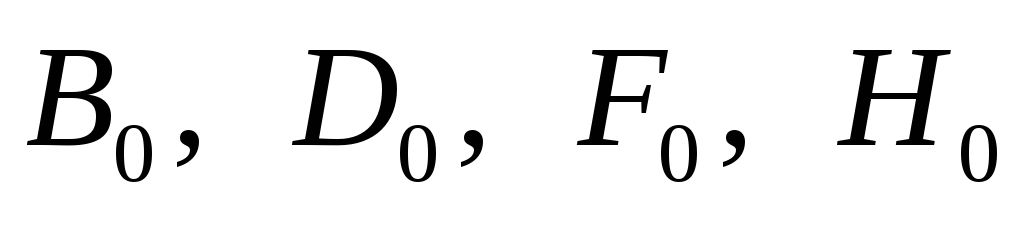 соответствуют значению параметра
соответствуют значению параметра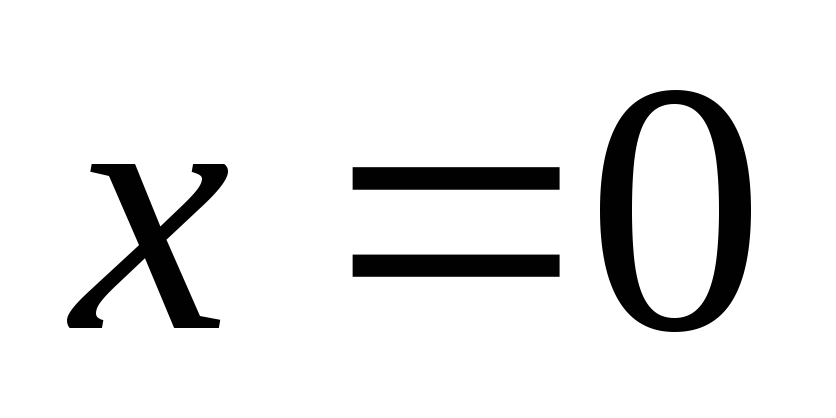 или
или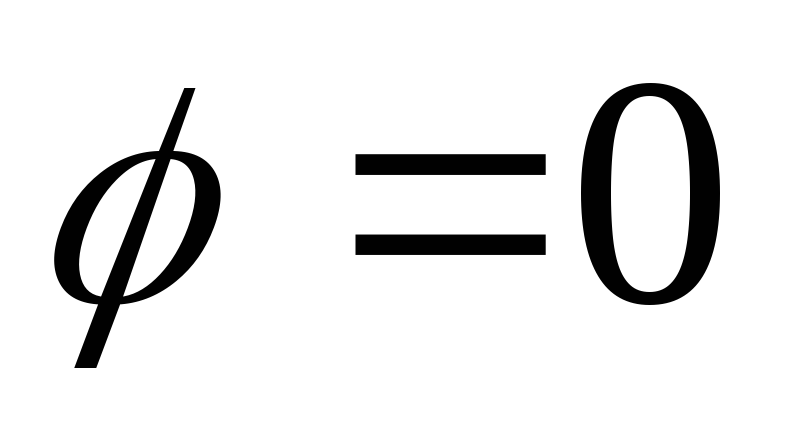 .
Зависимости коэффициентов
.
Зависимости коэффициентов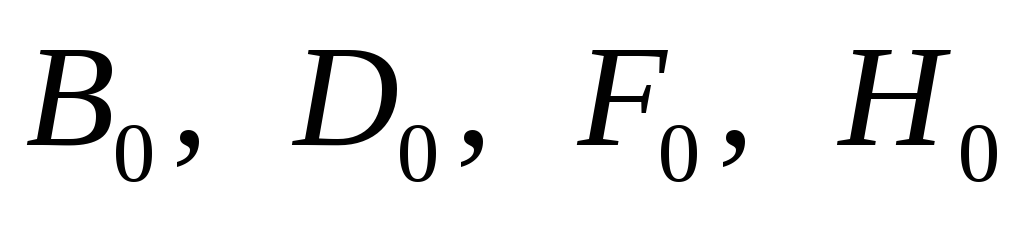 от функции параметра режима
от функции параметра режима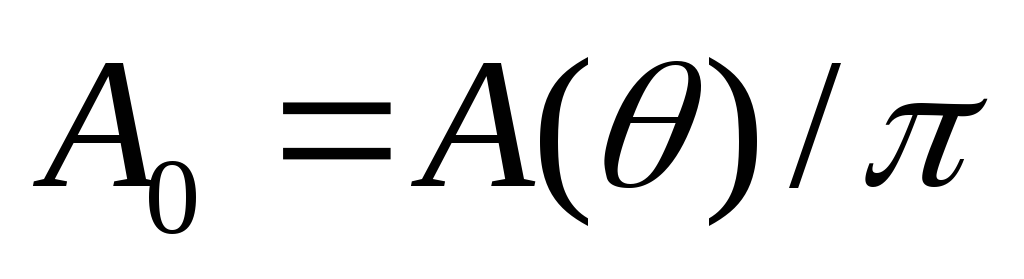 и угла
и угла приведены на рис. 2.5 — 2.9 [7, 8].
приведены на рис. 2.5 — 2.9 [7, 8].
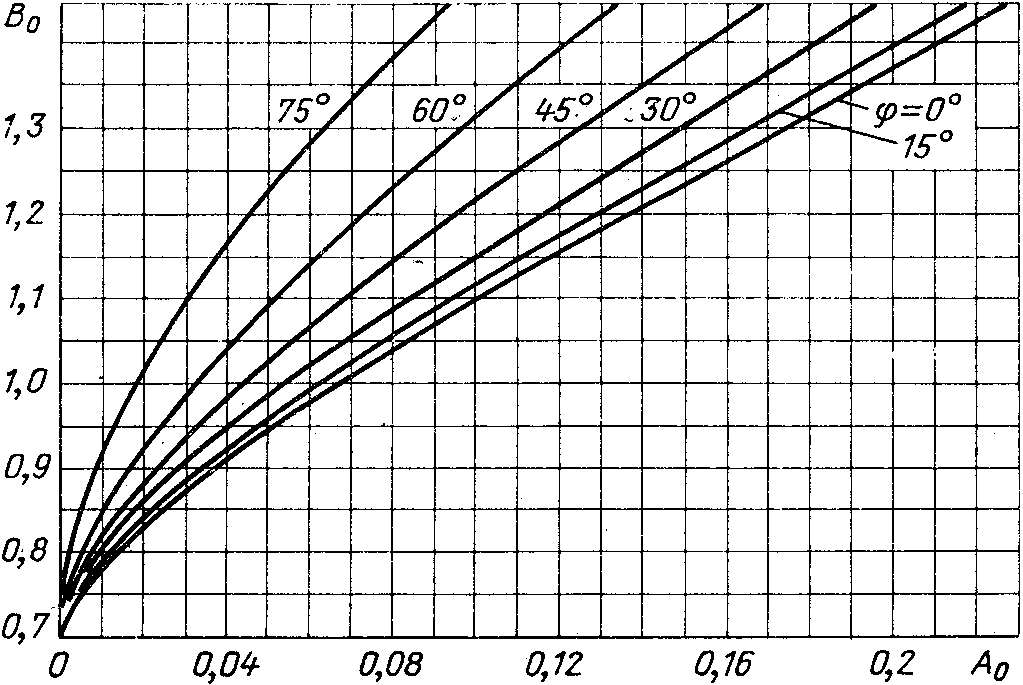
Рис.
2.5. Зависимость коэффициента 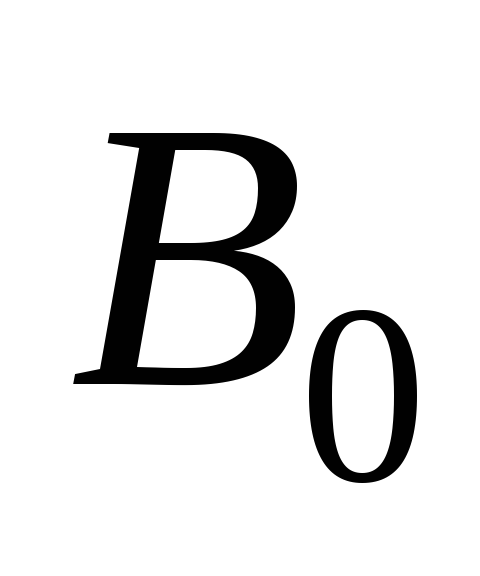 от
от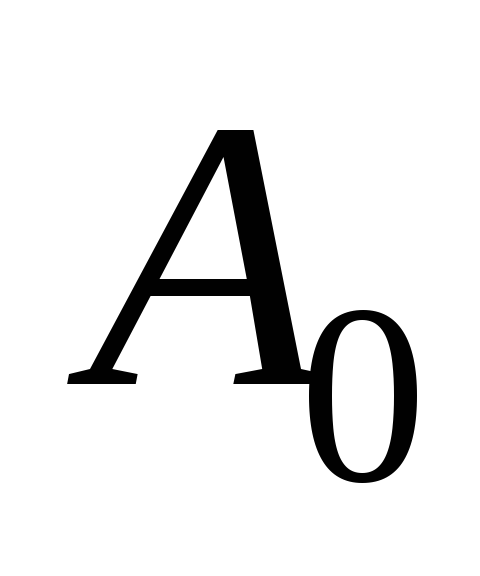 при различных значениях
при различных значениях .
.
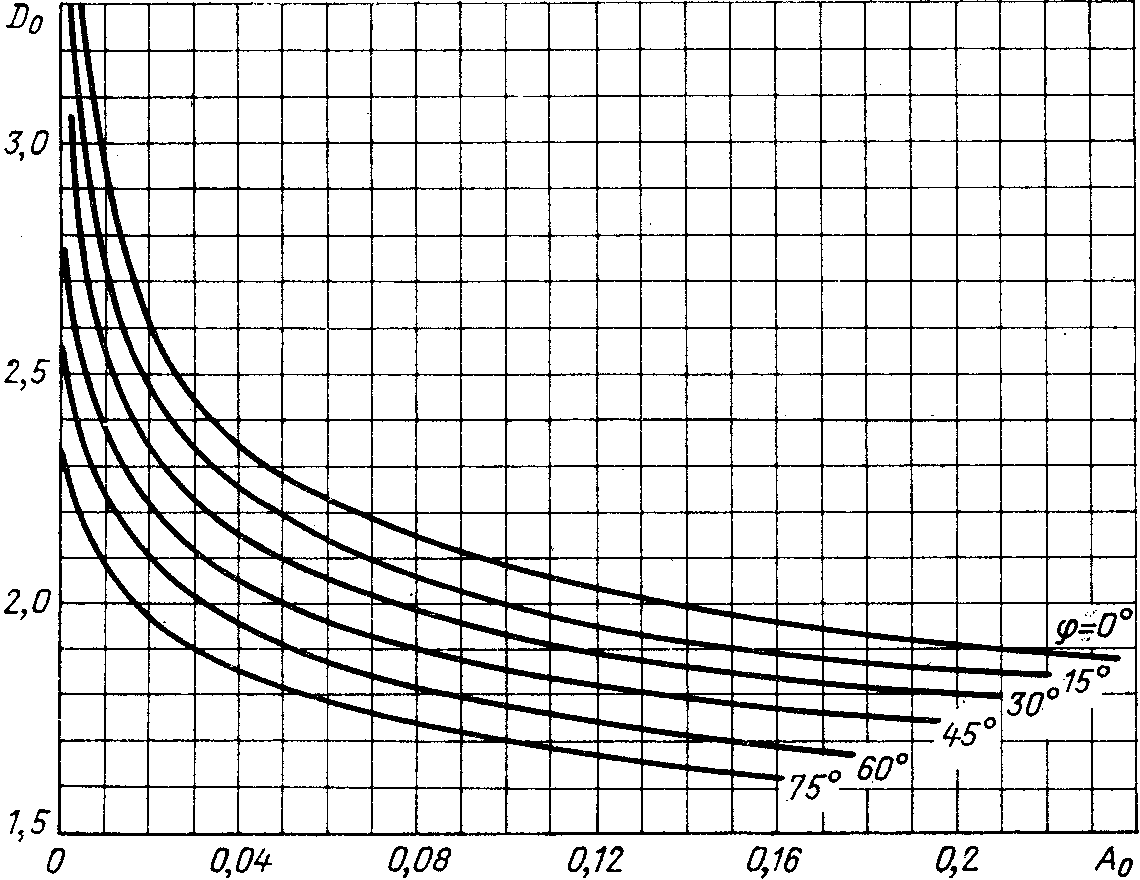
Рис.
2.6. Зависимость коэффициента  от
от при различных значениях
при различных значениях .
.
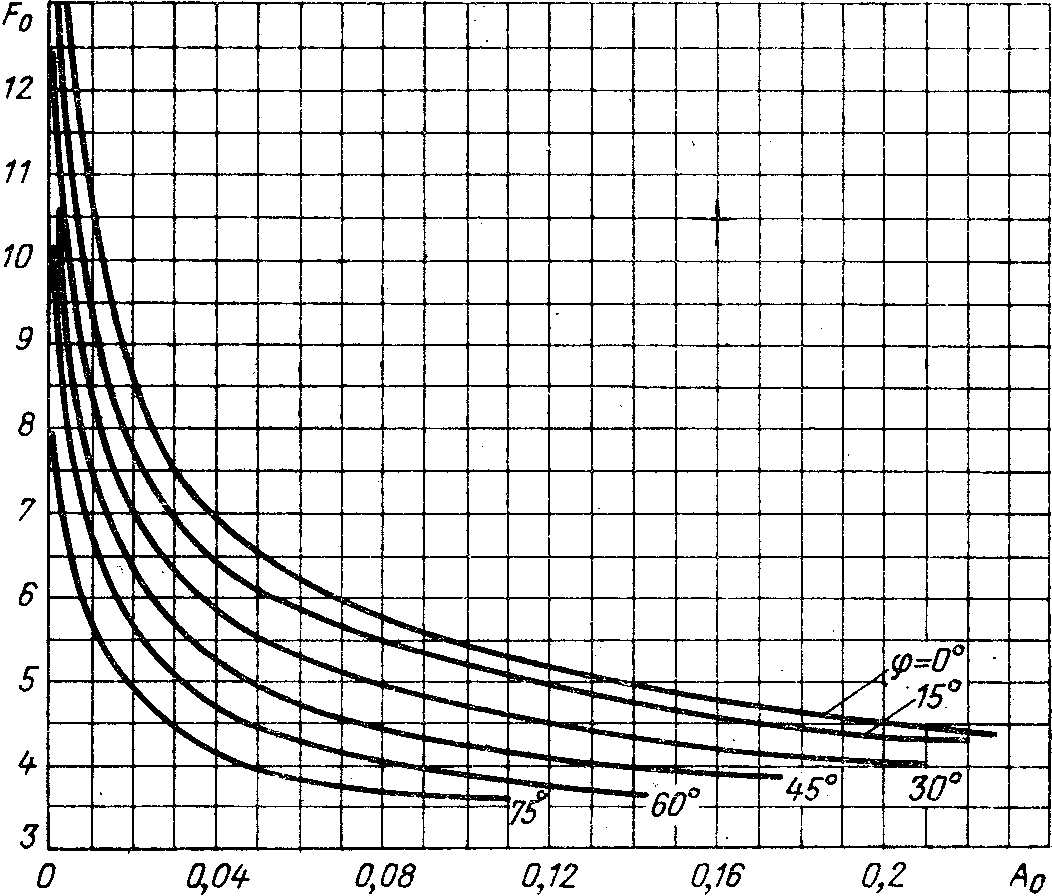
Рис.
2.7. Зависимость коэффициента  от
от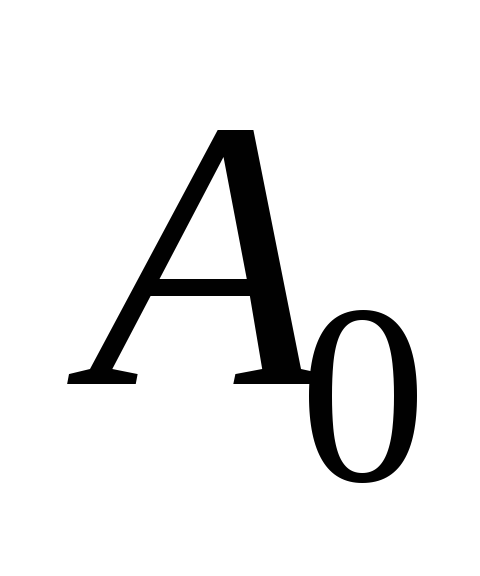 при различных значениях
при различных значениях .
.
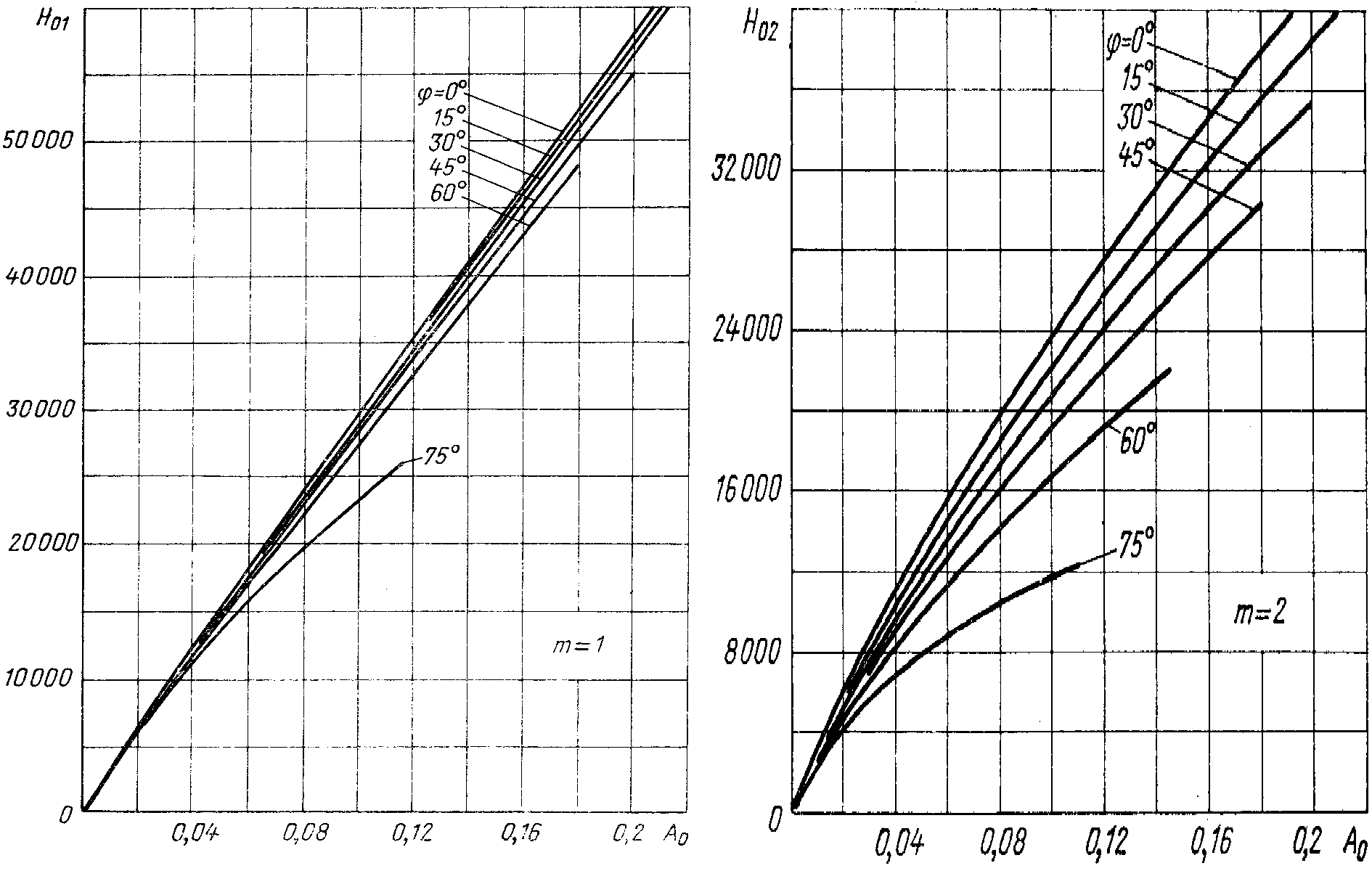
Рис.
2.8. Зависимости коэффициентов 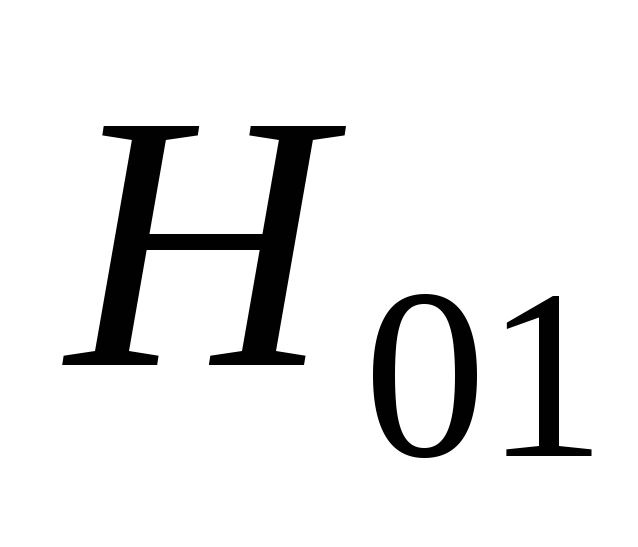 и
и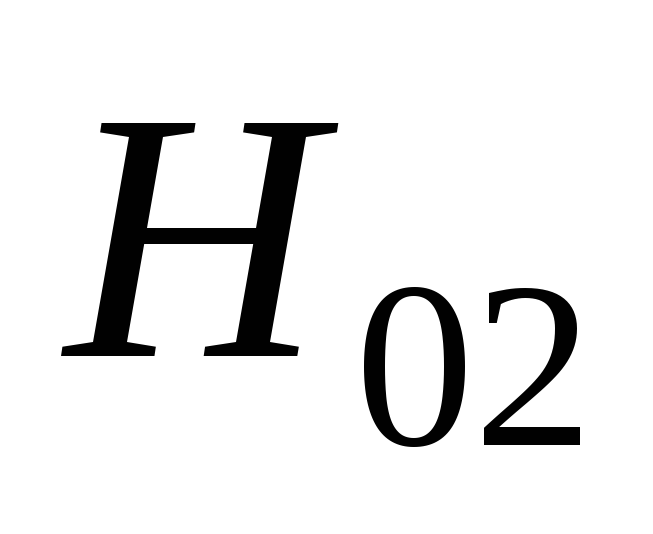 от
от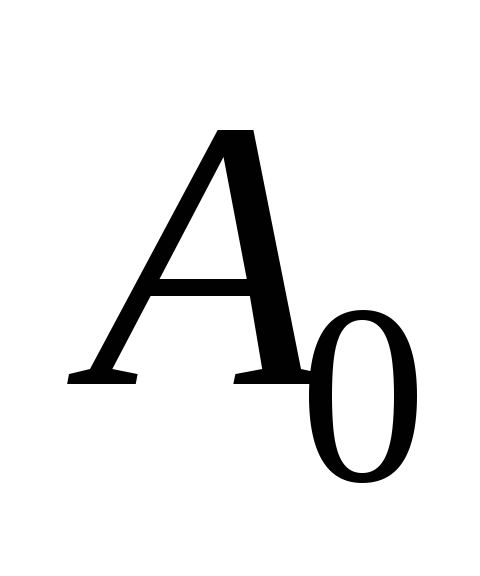 и
и .
.

Рис.
2.9. Зависимости коэффициентов 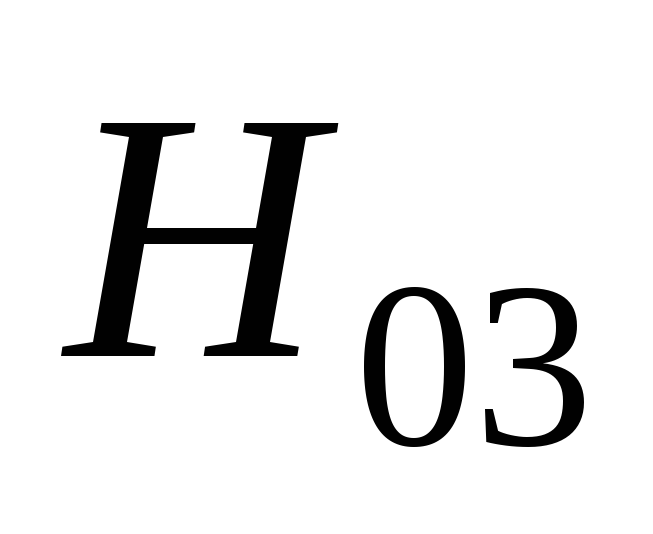 и
и от
от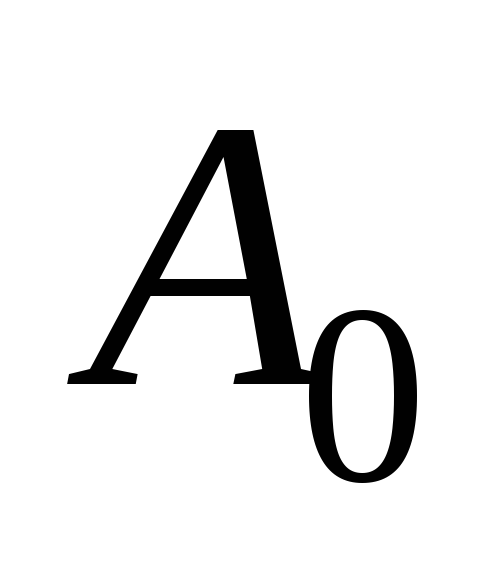 и
и .
.
Действующий ток 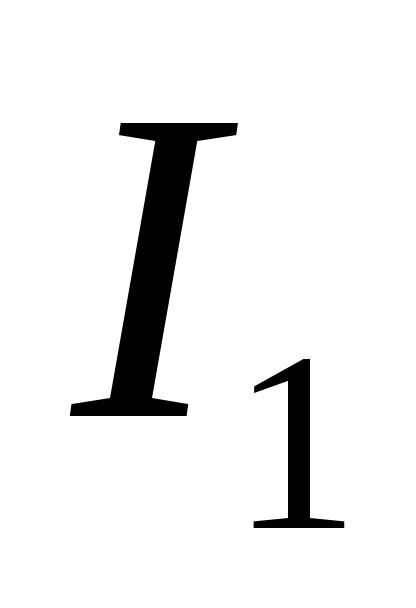 первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
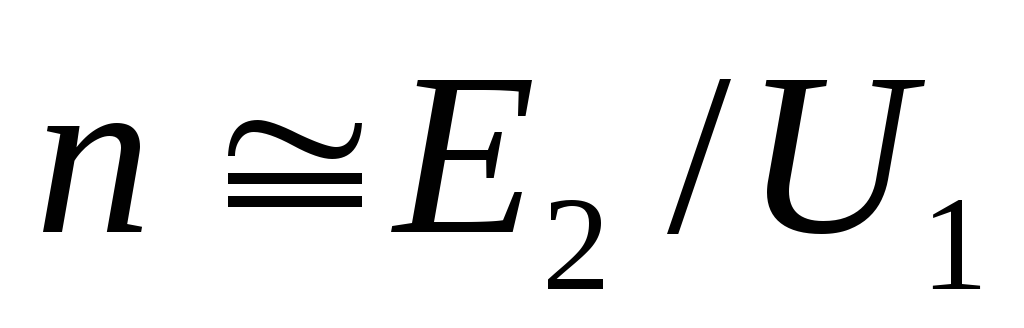 (2.22)
(2.22)
и
действующий ток во вторичных обмотках
трансформатора  .
.
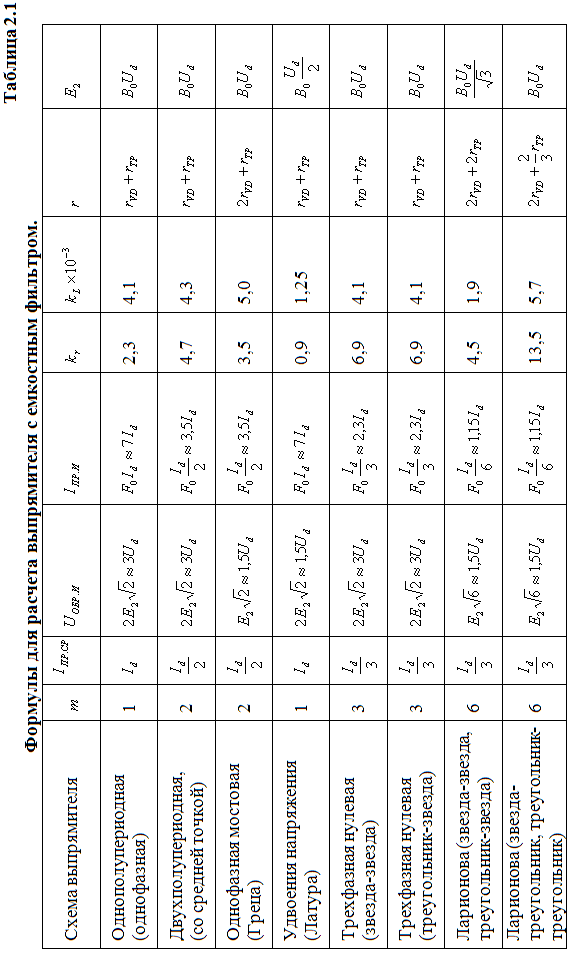
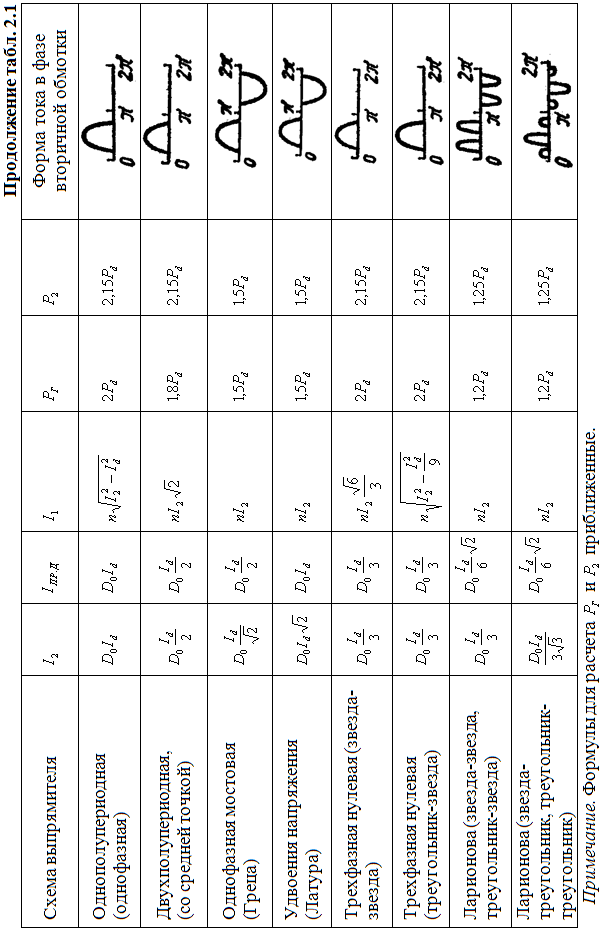
Габаритная мощность
трансформатора 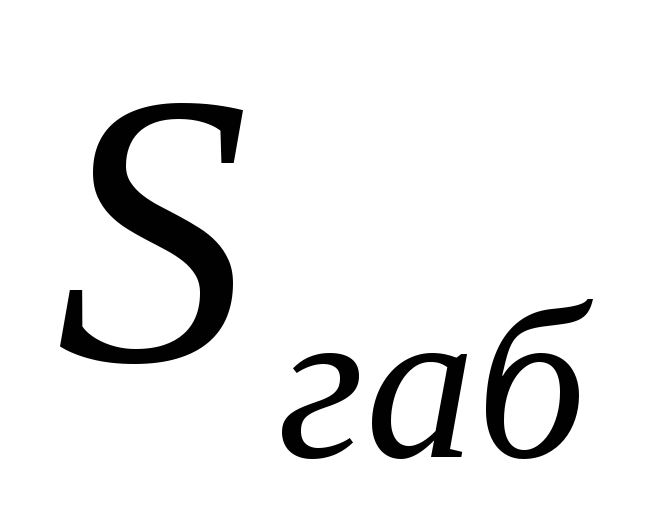 определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
Таблица 2.2.
Схема | Габаритная мощность трансформатора |
Однополупериодная |
|
Мостовая | |
2-х полупериодная со средней точкой |
|
3-х фазная нулевая |
|
Ларионова |
Внешнюю (нагрузочную) характеристику выпрямителя, т.е. зависимость выпрямленного напряжения от тока нагрузки, рассчитывают по формуле [8]:
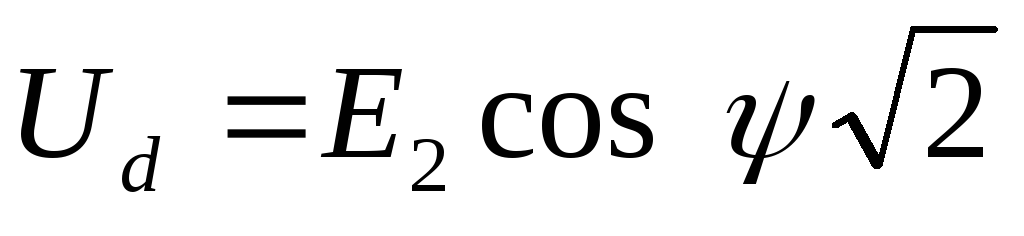 (2.23)
(2.23)
Задаваясь
различными значениями 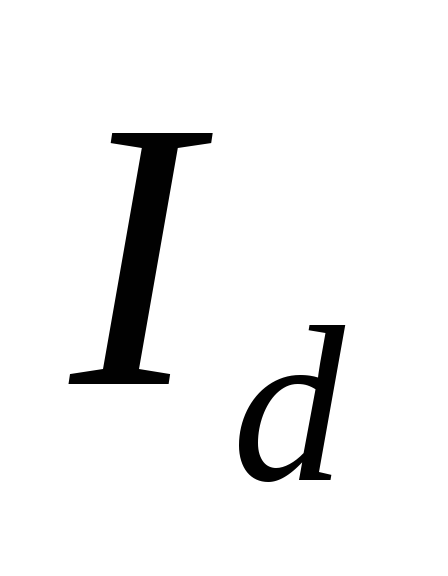 ,
определяют коэффициент
,
определяют коэффициент
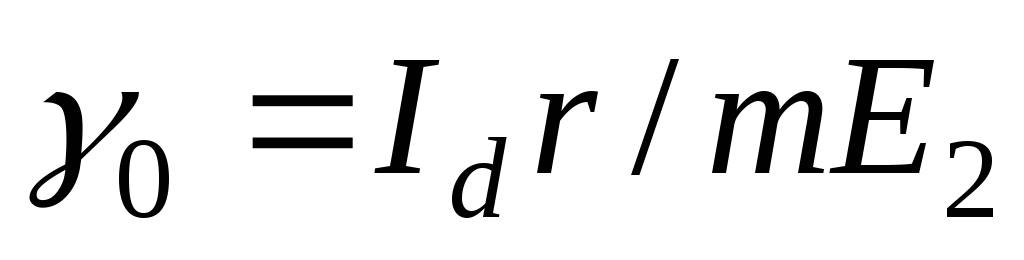 (2.24)
(2.24)
Значения 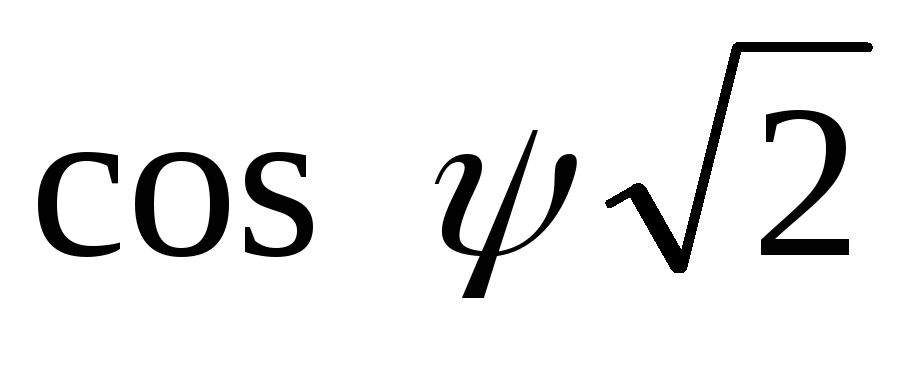 находят в зависимости от коэффициента
находят в зависимости от коэффициента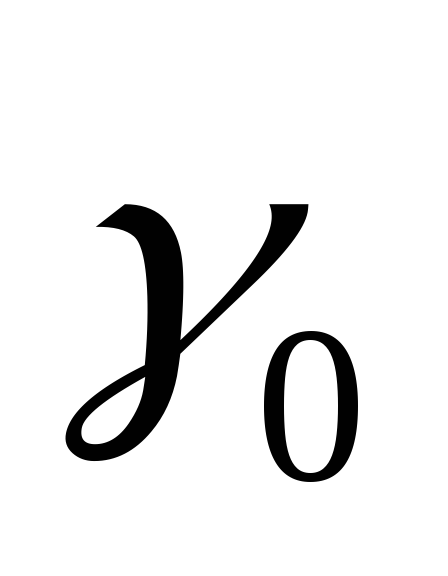 и угла φ по графику на риc.
2.10 [8]. Подставляя величину
и угла φ по графику на риc.
2.10 [8]. Подставляя величину 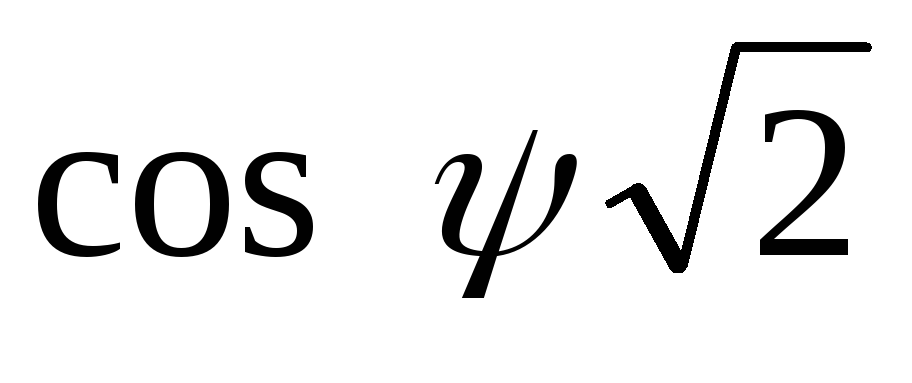 в формулу (2.23), находят
в формулу (2.23), находят для различных значений
для различных значений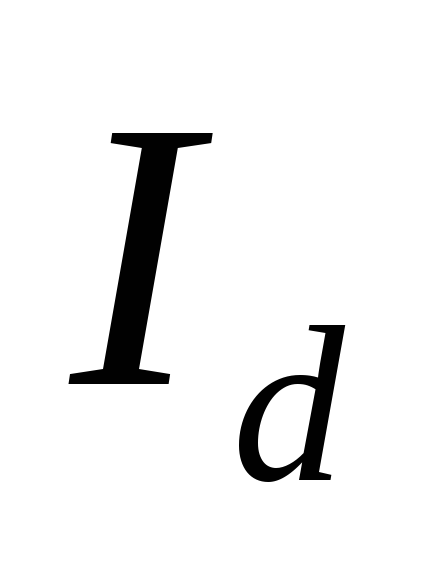 .
.
Напряжение на
конденсаторе будет равно напряжению
на нагрузке, но на случай отсоединения
нагрузки необходимо выбирать конденсатор
рассчитанный на напряжение
холостого хода выпрямителя – Uхх.
Очевидно, что при холостом ходе (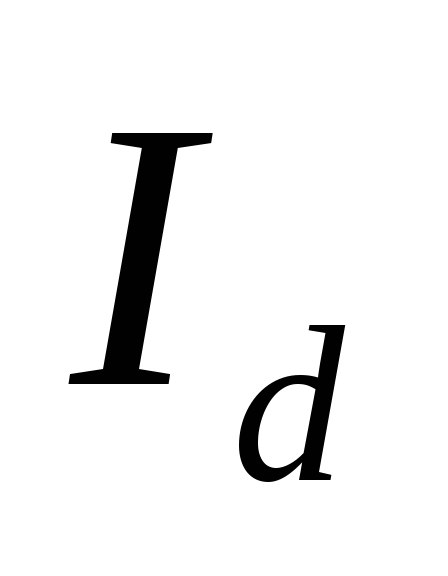 = 0)
= 0)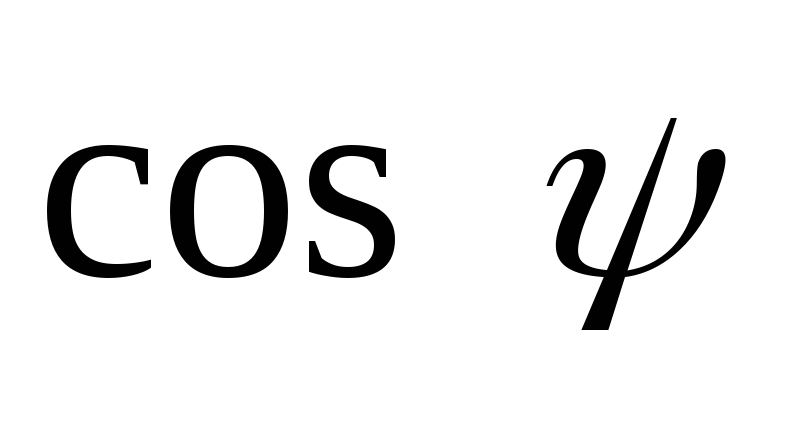 = 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
= 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
 (2.25)
(2.25)
В схеме Ларионова при соединении вторичной обмотки в звезду:
 (2.26)
(2.26)
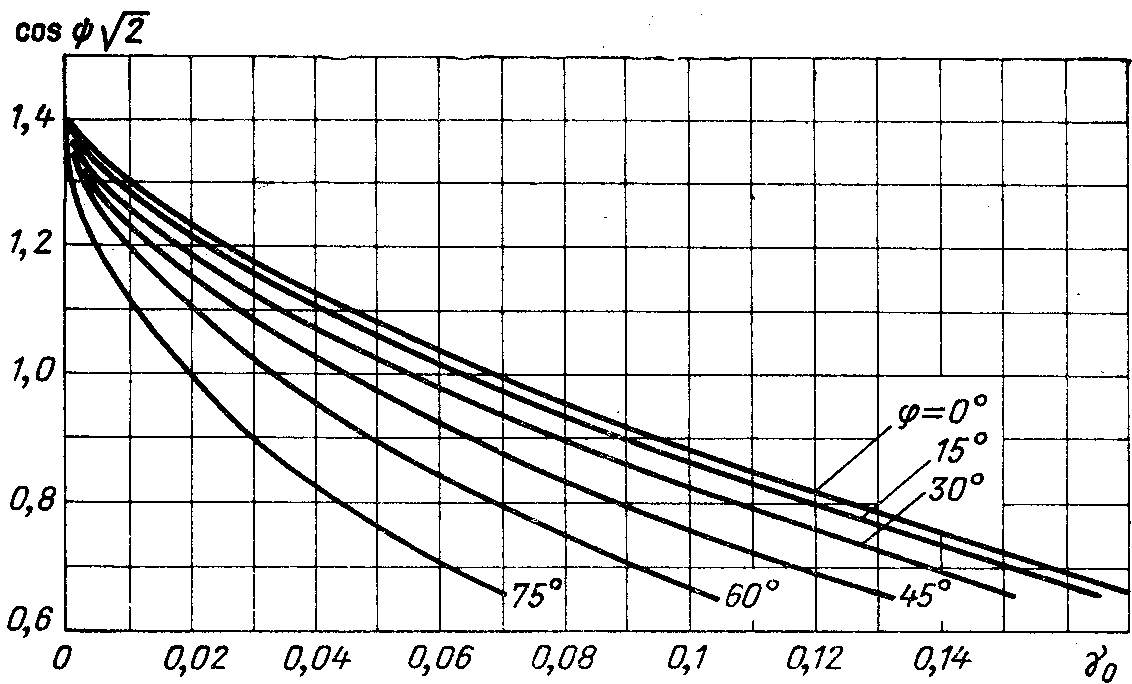
Рис.
2.10. Зависимость  от коэффициента
от коэффициента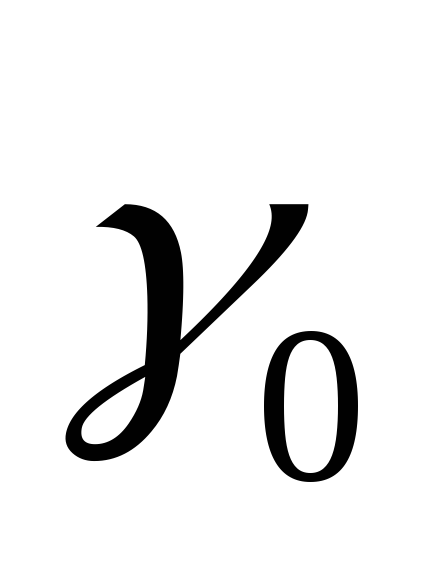
при различных значениях φ.
Учитывая то, что на фильтре знакопостоянное напряжение, конденсатор следует выбирать полярный, c номинальным напряжением не менее чем на 10% больше чем напряжение холостого хода выпрямителя (на случай скачков напряжения в электросети). Также следует учесть изменение емкости конденсатора в течение минимальной наработки, допустимое отклонение емкости, при этом допустимые напряжения переменной составляющей пульсирующего тока не должны превышать предельных значений для выбранного типа конденсатора. Переменная составляющая пульсирующего напряжения рассчитывается согласно (2.18). Поскольку допустимая переменная составляющая приводится в справочниках для частоты 50 Гц, ее следует пересчитать на частоту пульсаций напряжения на конденсаторе:
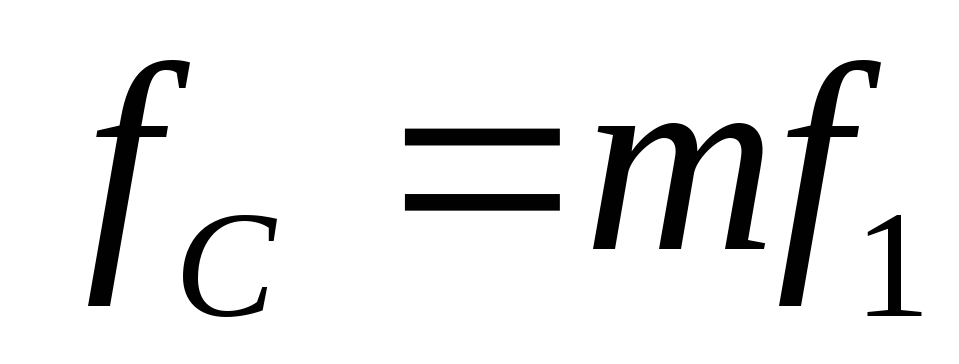 (2.27)
(2.27)
Приведенные соотношения получены для модели вентиля без порога выпрямления. Они обеспечивают хорошую точность расчета при выпрямленном напряжении более 15-20 В. При меньших значениях выпрямленного напряжения следует учитывать порог выпрямления [6].
ЭДС 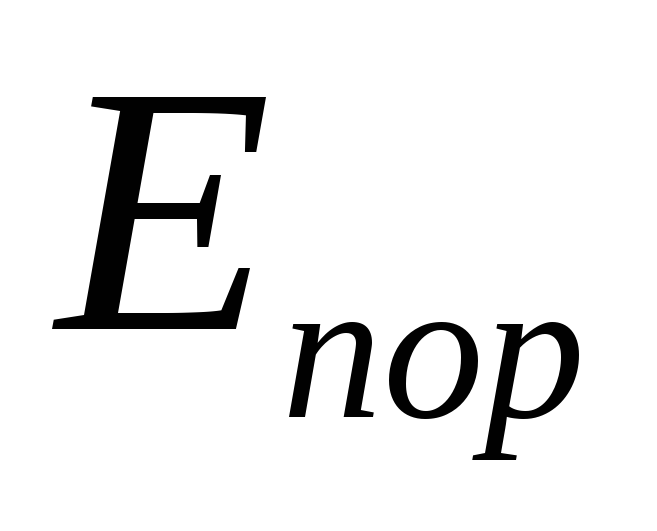 оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
Если считать напряжение:
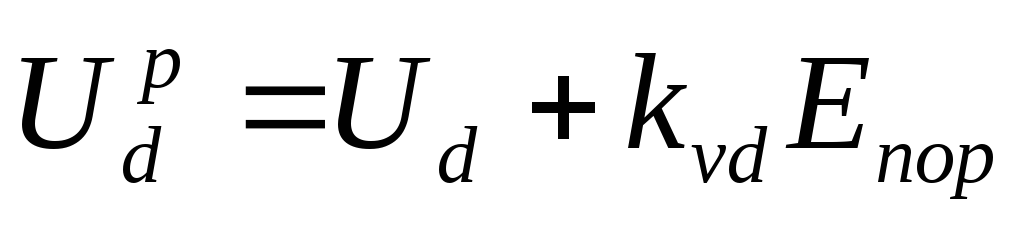 ,
(2.28)
,
(2.28)
которое
получается на выходном конденсаторе,
расчетным 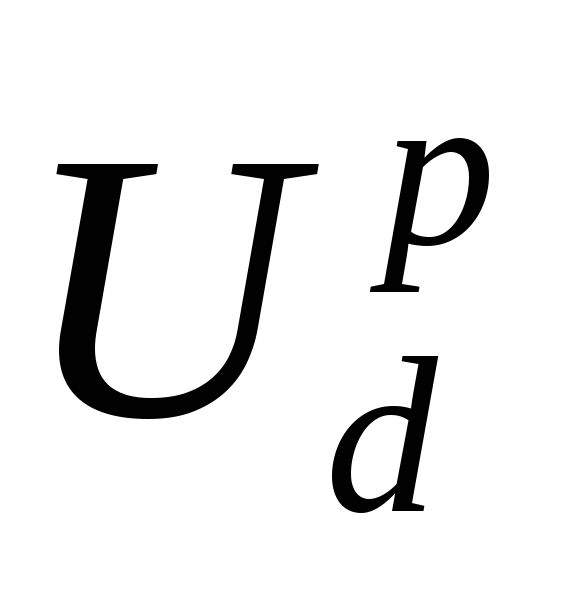 и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения
и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения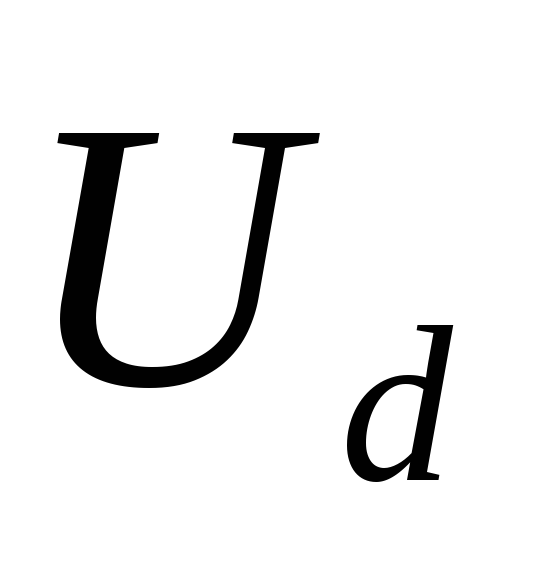 ,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент
,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент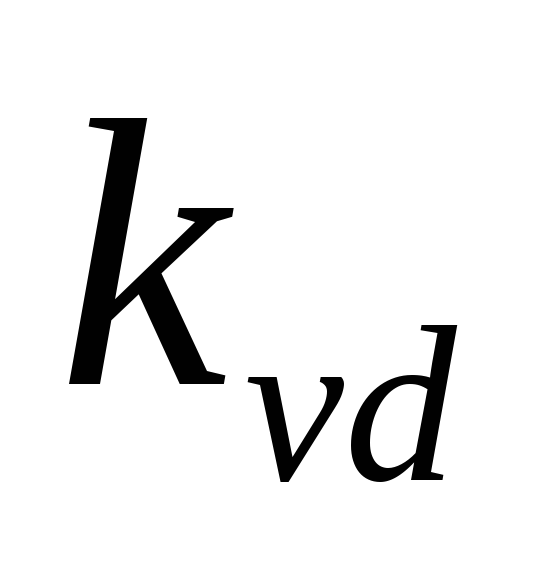 в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —
в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —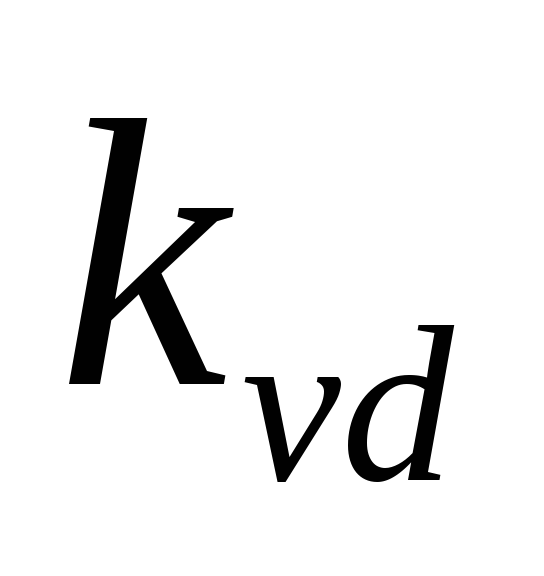 = 2, для остальных схем —
= 2, для остальных схем — = 1.
= 1.
Глава 2. Методики анализа и расчета выпрямителей
2.1. Анализ работы выпрямителя гармонического напряжения при нагрузке, начинающейся с емкостного элемента
Проведем анализ работы выпрямителя гармонического напряжения с нагрузкой, начинающейся с емкостного элемента, и рассмотрим процессы в многофазных схемах выпрямителей (рис. 2.1, а). Возьмем в качестве вентиля идеализированный диод с потерями, а в трансформаторе учтем только сопротивления обмоток. Примем за r сумму активных сопротивлений вентиля и обмоток трансформатора (рис. 2.1, б):
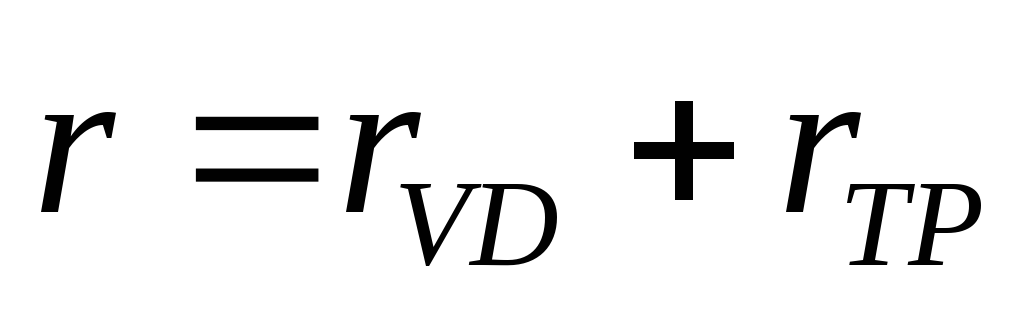 (2.1)
(2.1)
Рассмотрение
начнем с момента 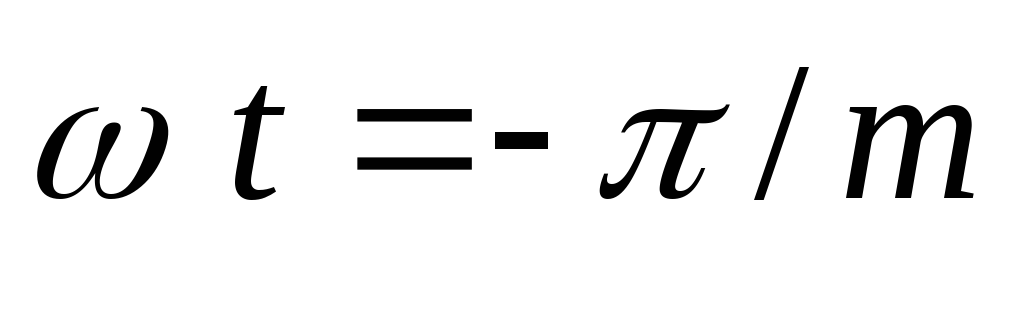 .
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При
.
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При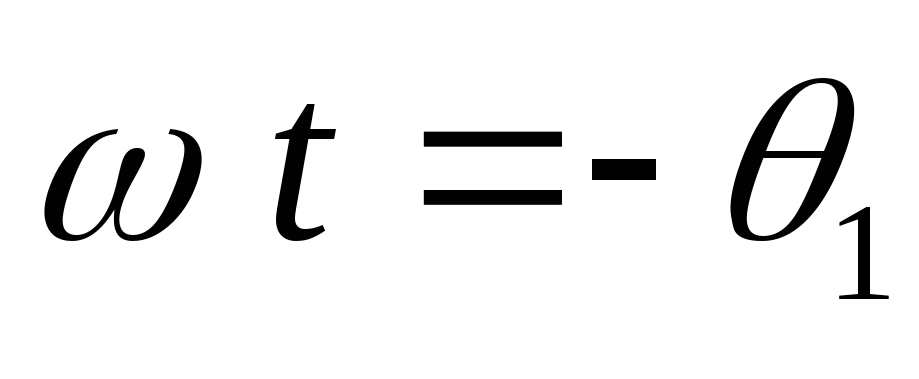 спадающее напряжение на конденсаторе
сравняется с возрастающей ЭДС первой
фазы
спадающее напряжение на конденсаторе
сравняется с возрастающей ЭДС первой
фазы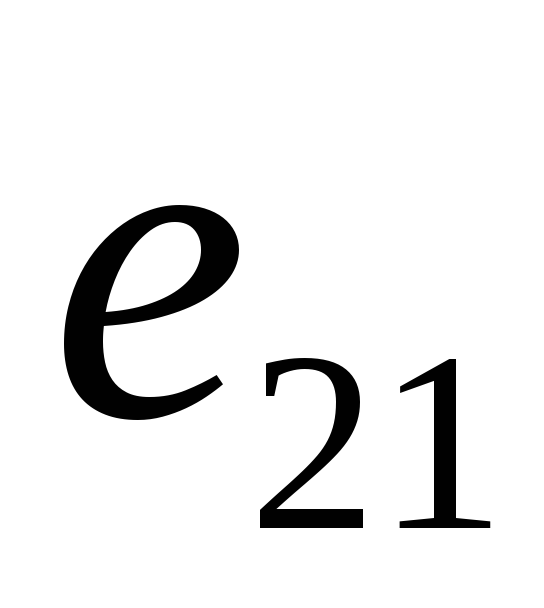 ,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку.
,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку.
При зарядке
конденсатора напряжение на нем растет
и при угле 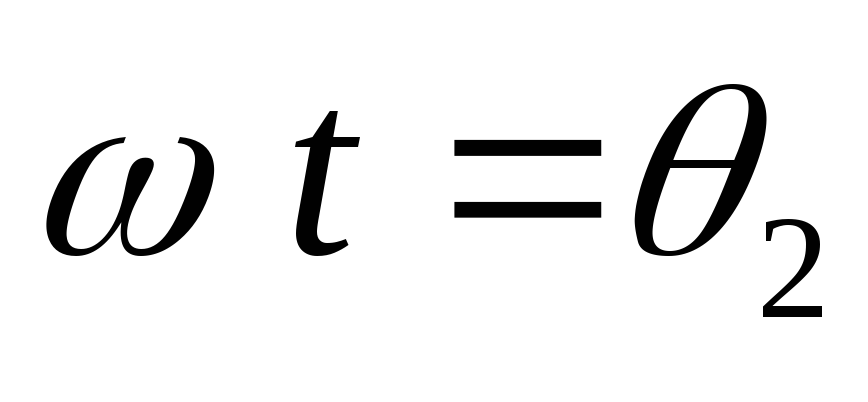 сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла
сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла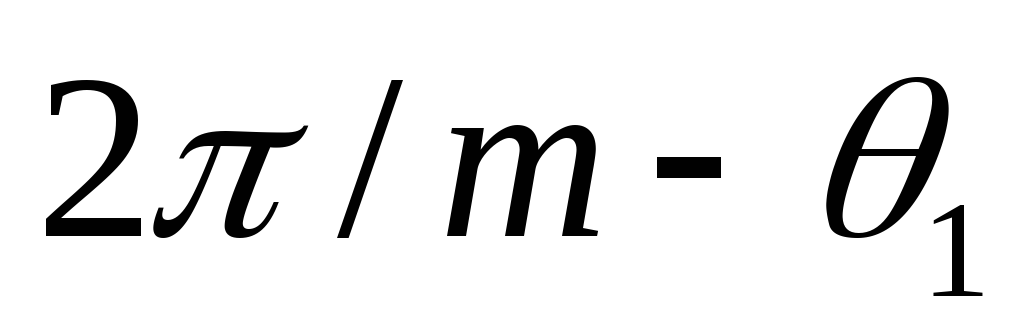 .
При угле
.
При угле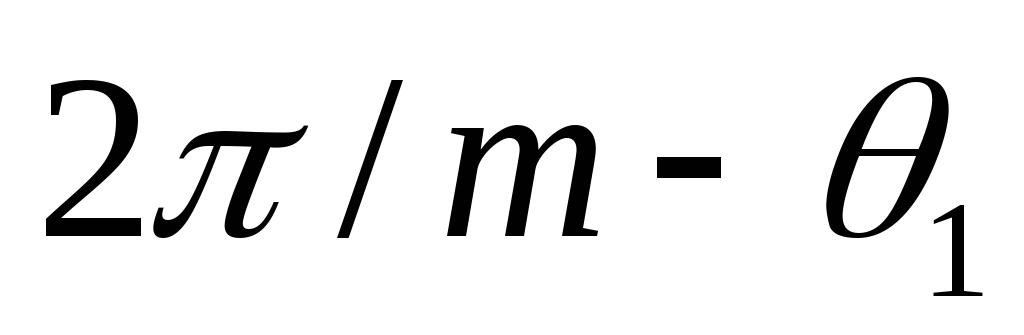 открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.
открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.
Определим ток вентиля, исходя из эквивалентной схемы открытой фазы (рис. 2.1, б). В данной схеме разность ЭДС фазы и выпрямленного напряжения получается из-за падения напряжения на сопротивлении r и, следовательно,
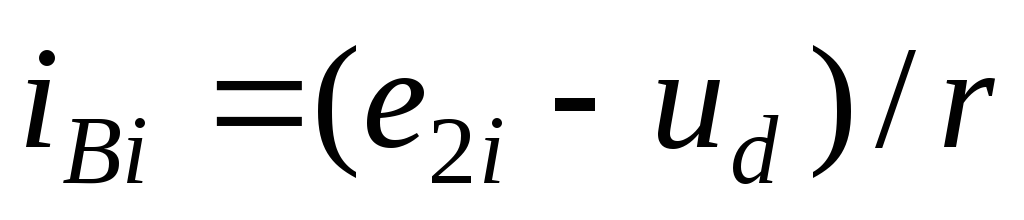 (2.2)
(2.2)
Таким образом, по форме ток вентиля совпадает с напряжением , равным разности ЭДС фазы и выпрямленного напряжения (рис. 2.1, в, г).
Импульс тока
вентиля второй фазы совпадает по значению
и форме с импульсом тока первой фазы,
но запаздывает на угол 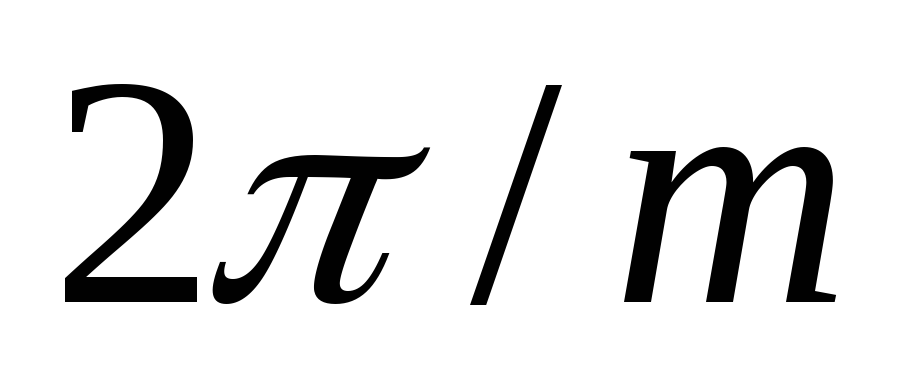 (рис. 2.1, д). Общий выпрямленный ток
(рис. 2.1, д). Общий выпрямленный ток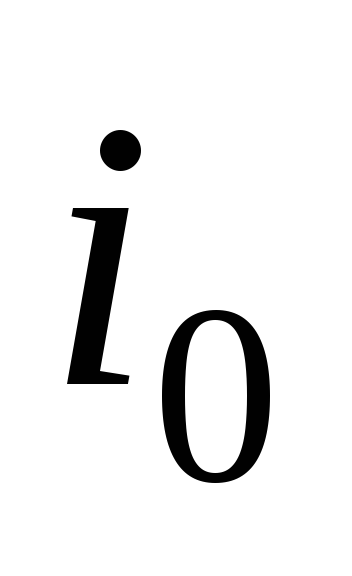 представляет собой сумму токов всех
вентилей, подходя к точкеа (рис. 2.1, а)
он делится. Часть его
представляет собой сумму токов всех
вентилей, подходя к точкеа (рис. 2.1, а)
он делится. Часть его  течет через нагрузку, а часть
течет через нагрузку, а часть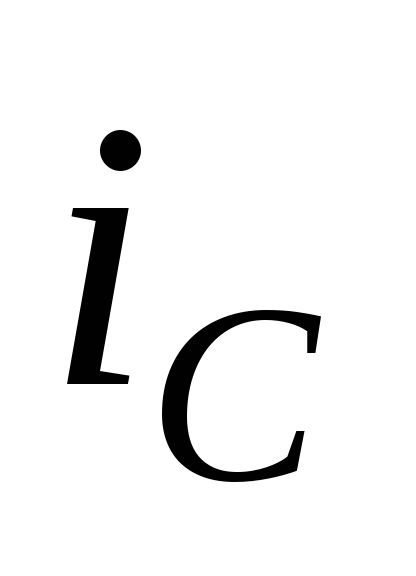 – через конденсатор. Ток
– через конденсатор. Ток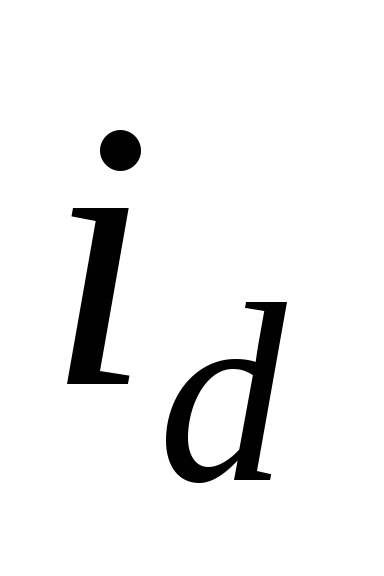 ,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
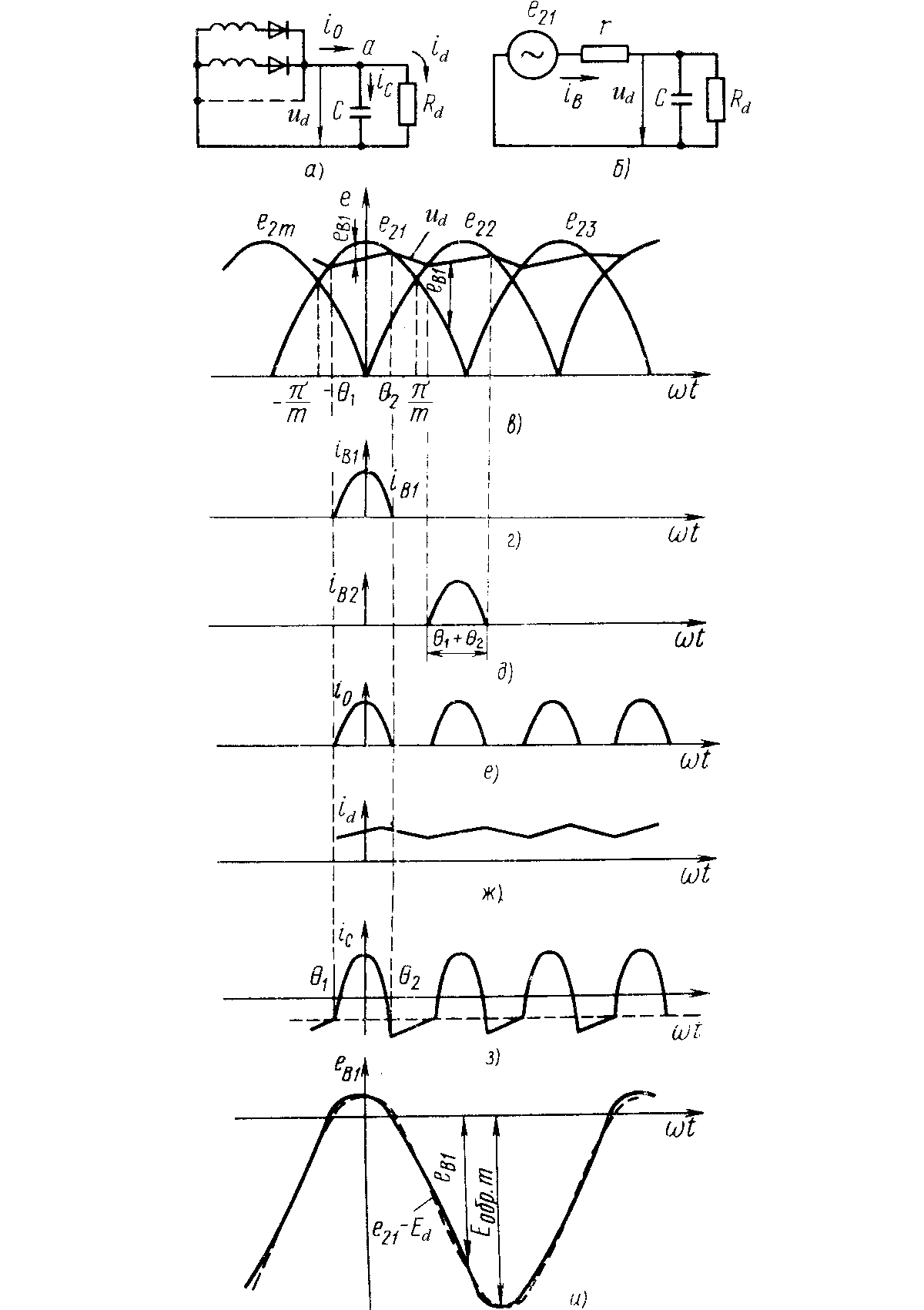
Рис. 2.1. Схемы (а, б) и диаграммы электромагнитных процессов выпрямителя гармонического напряжения с емкостным фильтром (в — и).
Напряжение на
вентиле первой фазы  меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода
меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода .
Отрицательное обратное напряжение
достигает максимума при
.
Отрицательное обратное напряжение
достигает максимума при :
:
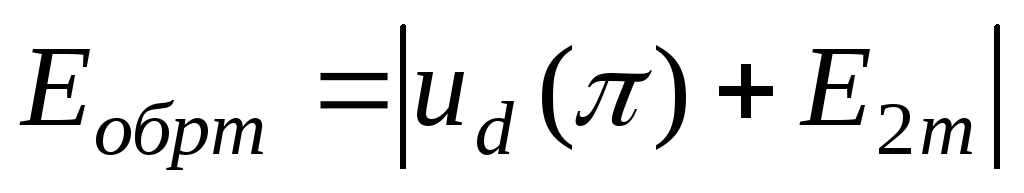 ,
(2.3)
,
(2.3)
что значительно больше выпрямленного напряжения.
Увеличение
сопротивления нагрузки 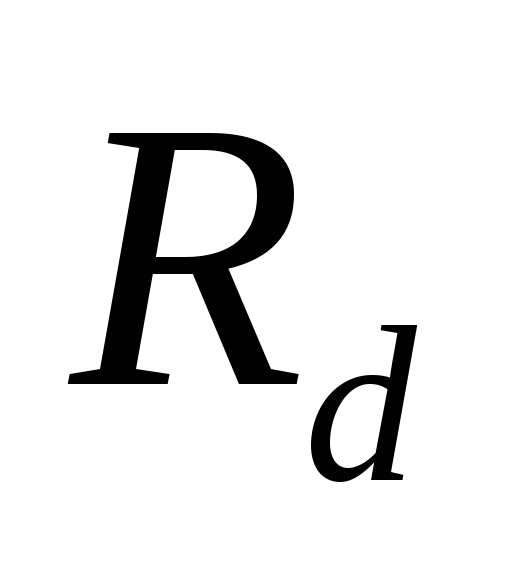 приводит к уменьшению тока нагрузки
приводит к уменьшению тока нагрузки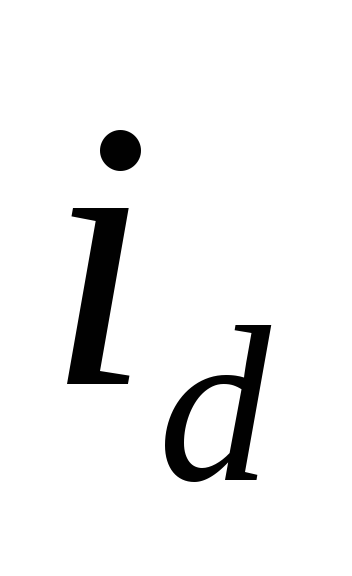 и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол
и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол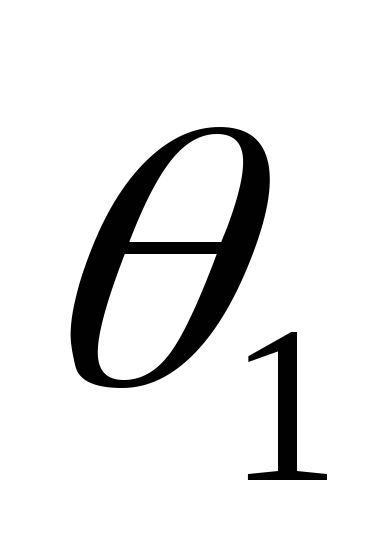 по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла
по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла .
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от
.
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от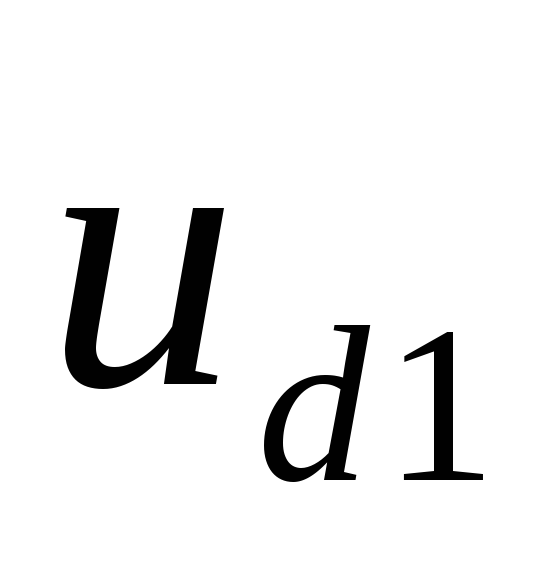 до
до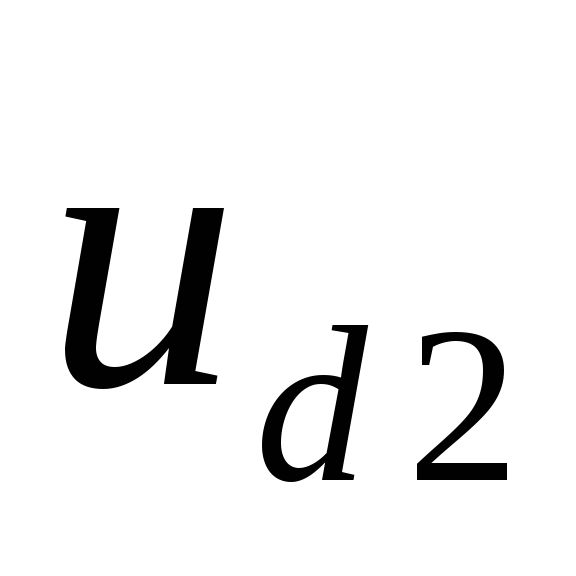 и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение
и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение ,
равное амплитуде ЭДС
,
равное амплитуде ЭДС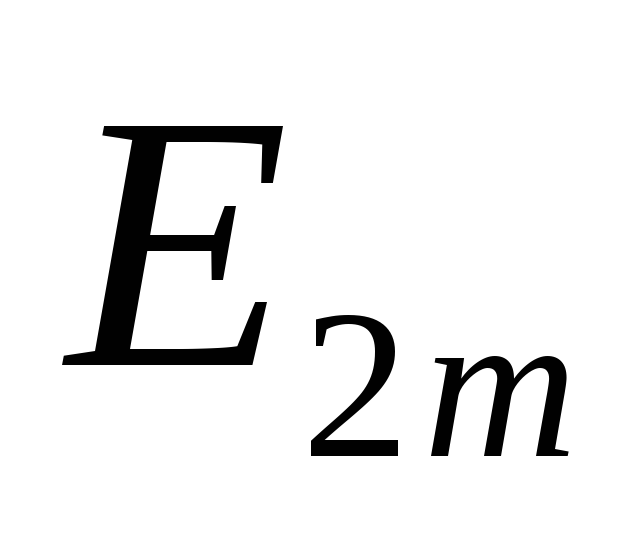 .
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
.
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
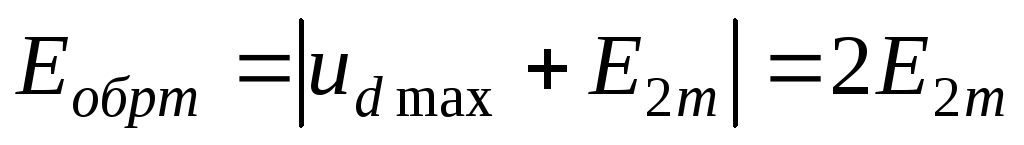 (2.4)
(2.4)
Из рассмотренного можно сделать вывод, что внешняя характеристика выпрямителя, работающего на нагрузку, начинающуюся с емкостного элемента, есть ниспадающая кривая (рис. 2.2, в), а угол отсечки зависит от тока нагрузки.
Емкость конденсатора
сказывается не только на пульсациях
выпрямленного напряжения, но и на форме
импульса тока вентиля. При очень большой
емкости конденсатора выходное напряжение
почти постоянно и импульс тока симметричен,
т.к. углы отсечки 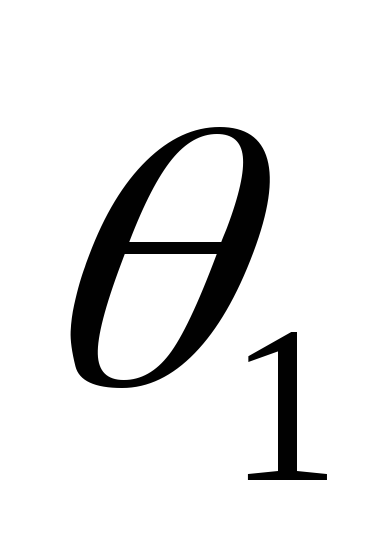 и
и равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки
равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки становится больше угла
становится больше угла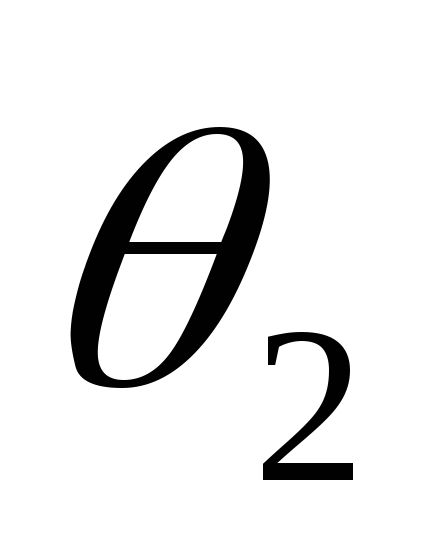 .
.
В итоге необходимо отметить следующее [6]:
1) при нагрузке, начинающейся с конденсатора, выпрямитель работает с отсечкой тока. Импульсы тока вентилей имеют длительность, меньшую T/m;
2) выпрямленное напряжение и ток нагрузки имеют пилообразную форму;
3) чем больше ток нагрузки, тем больше угол отсечки тока и тем меньше выпрямленное напряжение;
4) емкость конденсатора определяет как напряжение пульсаций, так и отклонение от косинусоидальной формы импульса тока.
С уменьшением сопротивления фазы r зарядный ток возрастает и напряжение на выходном конденсаторе нарастает круче, чем это показано на рис. 2.1, в.
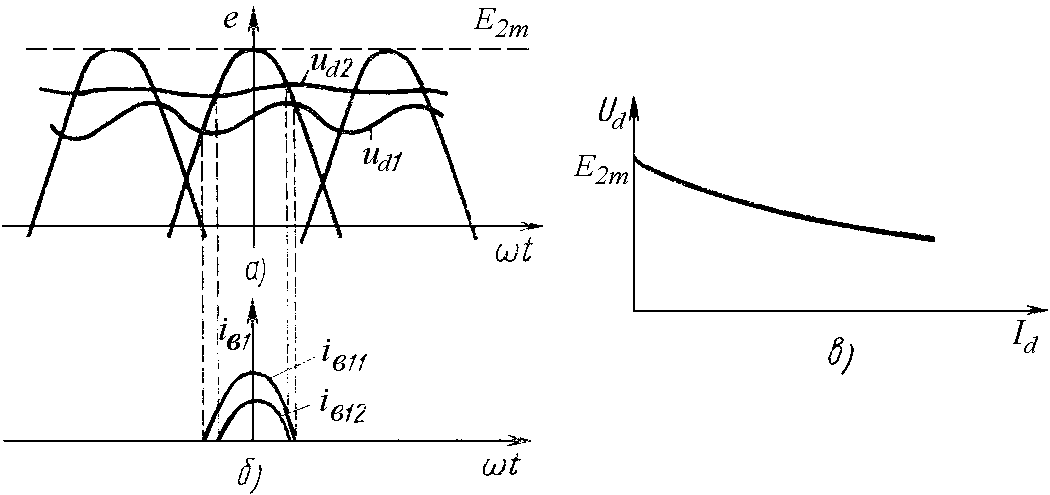
Рис.
2.2. Диаграммы электромагнитных процессов
(а, б) для нагрузок 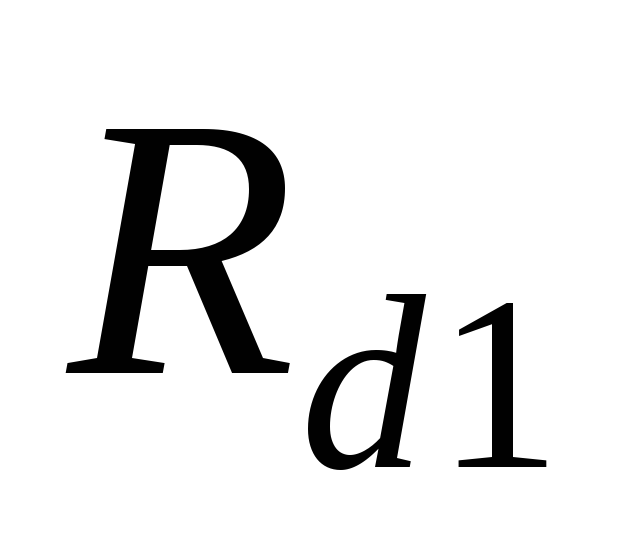 и
и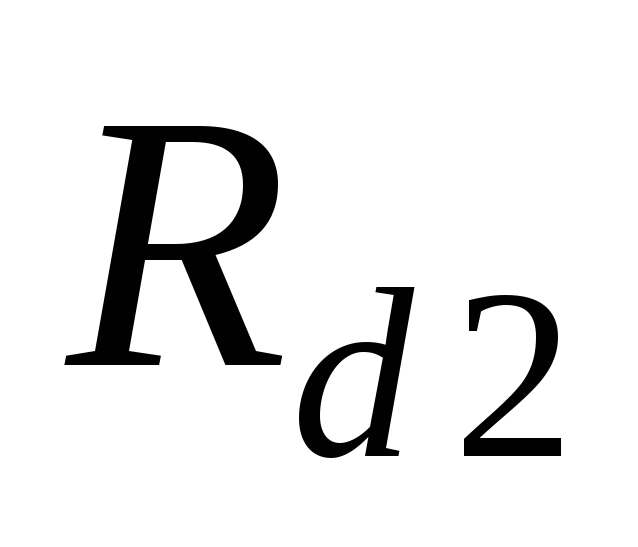 (
(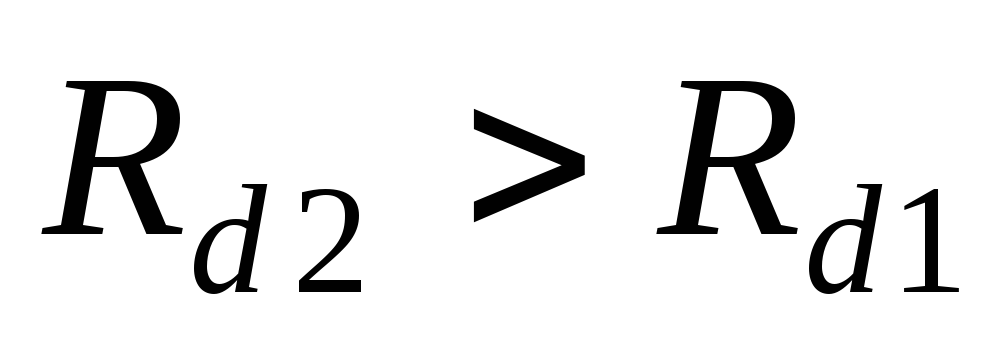 )
и внешняя характеристика выпрямителя
(в).
)
и внешняя характеристика выпрямителя
(в).
В бестрансформаторных выпрямителях сопротивление вентилей и проводов, подводящих энергию к выпрямителю, настолько мало, что напряжение на конденсаторе при его зарядке следует за ЭДС работающей фазы (рис. 2.3, а). При этом ток вентиля:
 ,
(2.5)
,
(2.5)
где 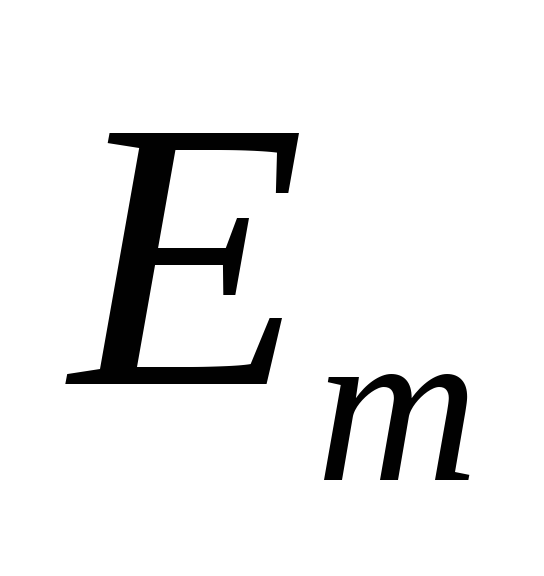 — амплитуда фазного напряжения сети,
— амплитуда фазного напряжения сети,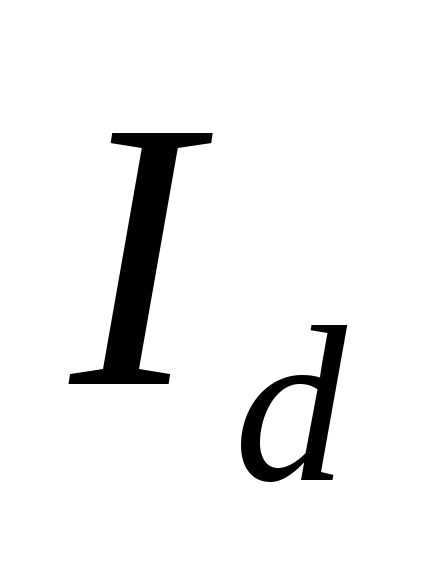 — ток нагрузки, принятый постоянным.
— ток нагрузки, принятый постоянным.
По сравнению со
случаем, когда зарядный ток ограничивался
сопротивлением зарядной цепи, импульс
тока (рис. 2.3, б) становится асимметричным.
Выходной конденсатор выпрямителя
заряжается до напряжения 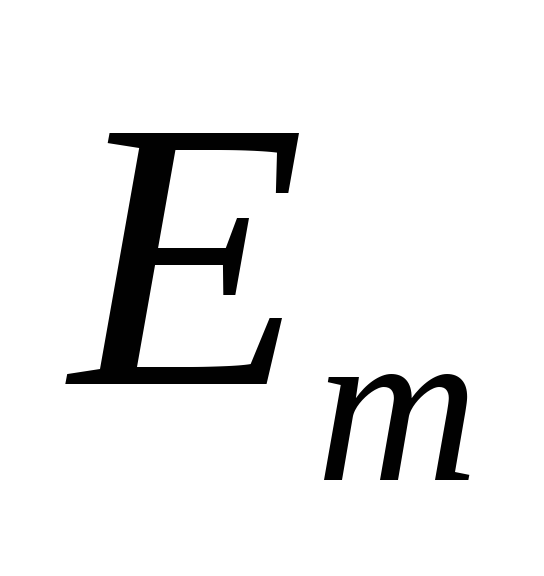 от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла(первая фаза). При
от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла(первая фаза). При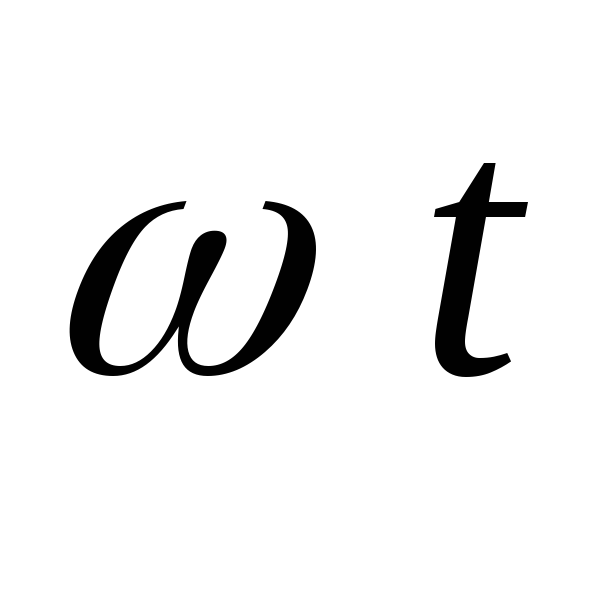 >
0 ток вентиля становится меньше тока
нагрузки и при
>
0 ток вентиля становится меньше тока
нагрузки и при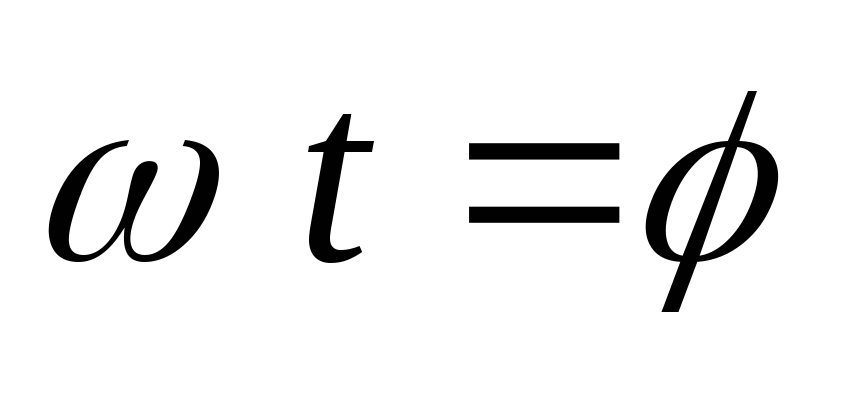 достигает нуля, вентиль закрывается.
Положив в (2.5)
достигает нуля, вентиль закрывается.
Положив в (2.5) ,
получим выражение для определения угла
выключения вентилей
,
получим выражение для определения угла
выключения вентилей :
:
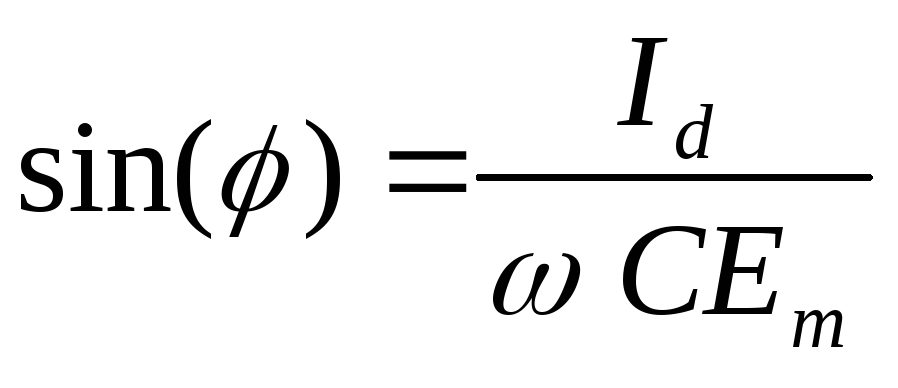 (2.6)
(2.6)
При 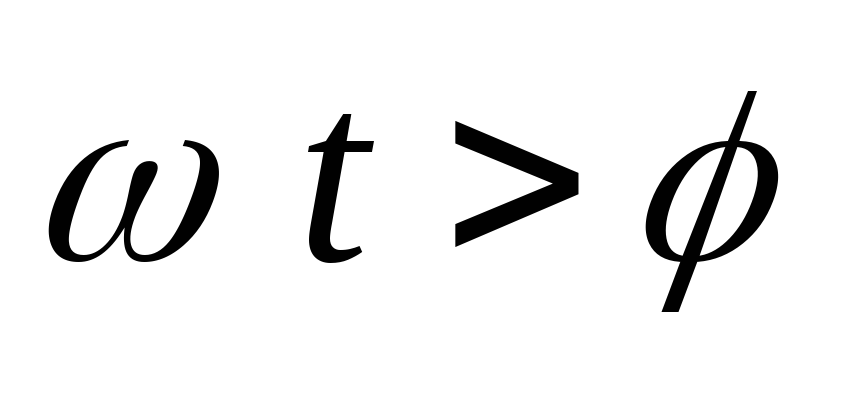 напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения
напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения  ,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы
,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы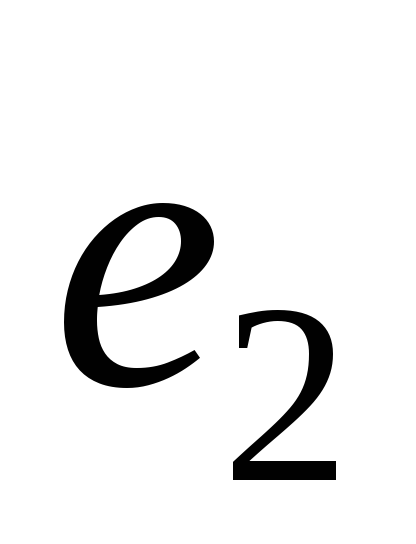 ,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
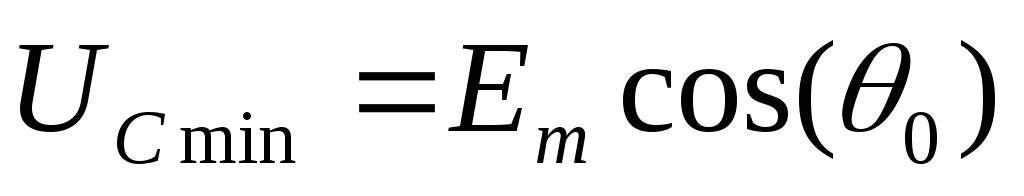 (2.7)
(2.7)
Углы  и
и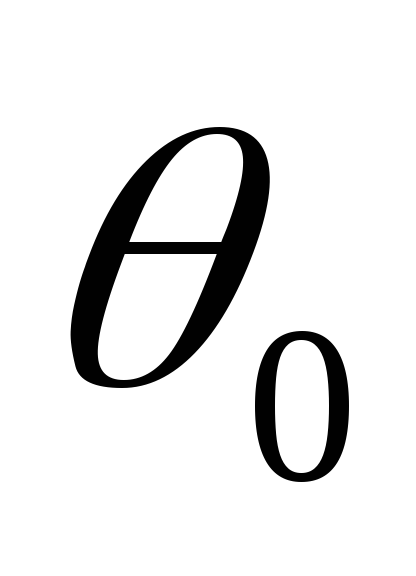 связаны нелинейной зависимостью (рис.
2.3, в).
связаны нелинейной зависимостью (рис.
2.3, в).

Рис.
2.3. Диаграммы электромагнитных процессов
в бестрансформаторном выпрямителе (а,
б) и зависимость углов  и
и (в).
(в).
Среднее значение выпрямленного напряжения мало отличается от:
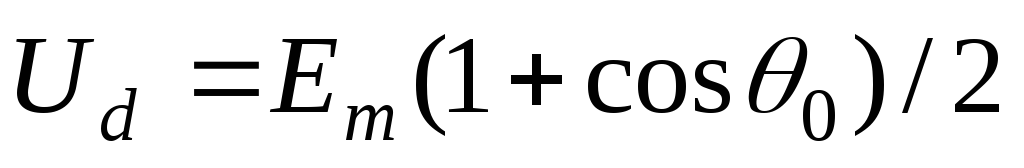 ,
(2.8)
,
(2.8)
которое
получилось бы при линейном нарастании 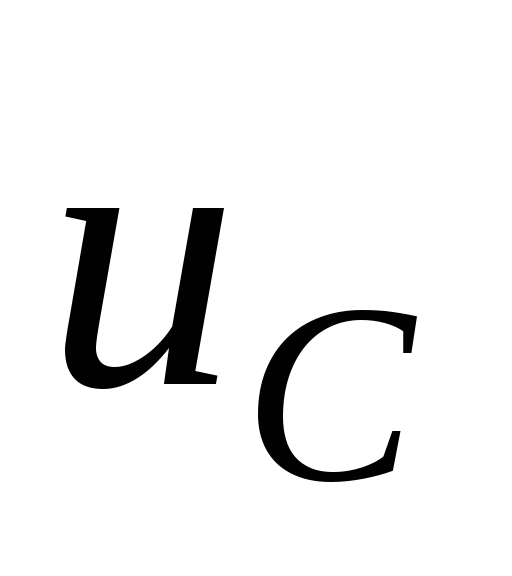 при зарядке конденсатора.
при зарядке конденсатора.
Важно отметить
заметную зависимость выходного напряжения
выпрямителя от емкости выходного
конденсатора. При увеличении емкости С спадание напряжения из-за разрядки
конденсатора замедляется и угол
открывания вентиля  становится меньше.
становится меньше.
Таким образом, при расчете выпрямителя пользуются двумя расчетными моделями [6]. Первую расчетную модель применяют при расчетах трансформаторных выпрямителей, когда ток зарядки выходного конденсатора ограничивается активным и индуктивным сопротивлением фазы трансформатора, а также сопротивлением вентиля.
Вторая модель хорошо отражает процессы в бестрансформаторном выпрямителе. В нее закладываются малые активное и индуктивное сопротивление фазы сети и малое падение напряжения на вентилях.
Поскольку характер
выпрямителей определяется не только
сопротивлением зарядной цепи, а и
емкостью выходного конденсатора, т.е.
постоянной времени заряда, применимость
первой или второй моделей зависит от
соотношения сопротивлений фаз r и 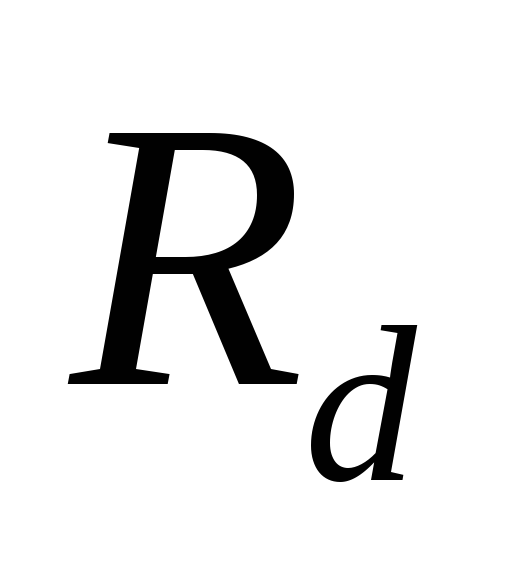 и емкости выходного конденсатораС [6].
и емкости выходного конденсатораС [6].
Пояснить методику
получения расчетных формул для первой
модели проще всего при анализе схемы
выпрямителя, приведенной на рис. 2.1, б,
где ток зарядки конденсатора ограничивается
сопротивлением r.
Так как выпрямитель всегда характеризуется
относительно небольшим напряжением
пульсаций (его значение ограничивают
допустимой реактивной мощностью
выходного конденсатора фильтра на
уровне 5-10% от 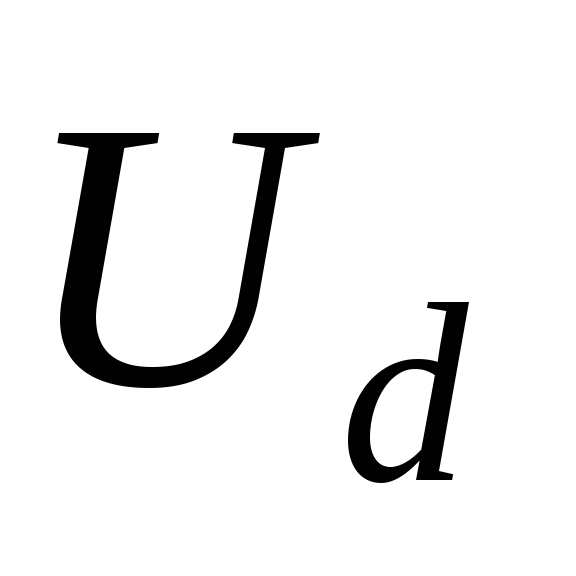 ),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки
),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки 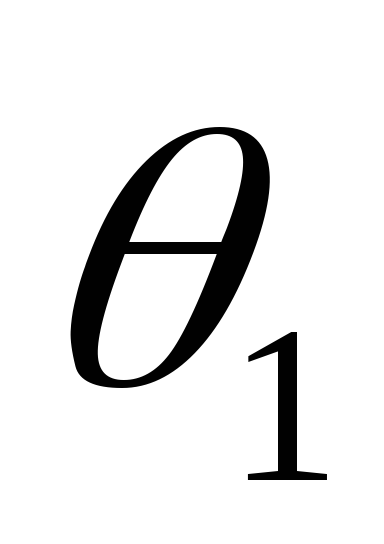 и
и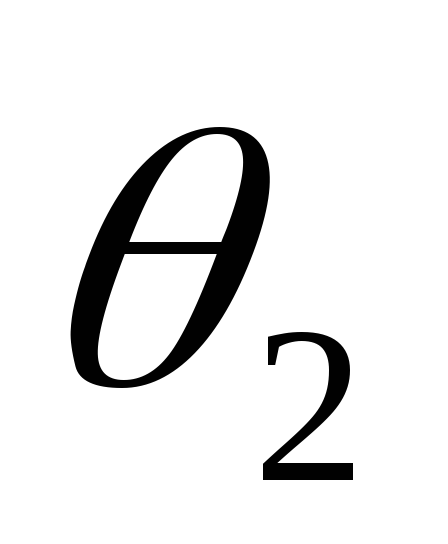 становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
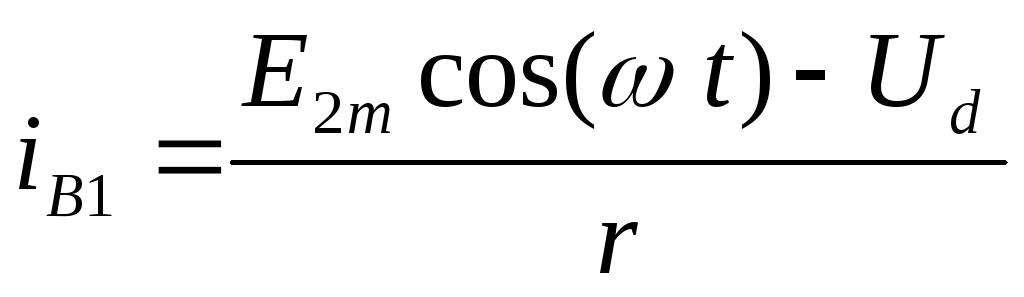 (2.9)
(2.9)
при  и
и на остальной части периода.
на остальной части периода.
Постоянный ток в нагрузке выпрямителя равен сумме постоянных составляющих токов всех вентилей:
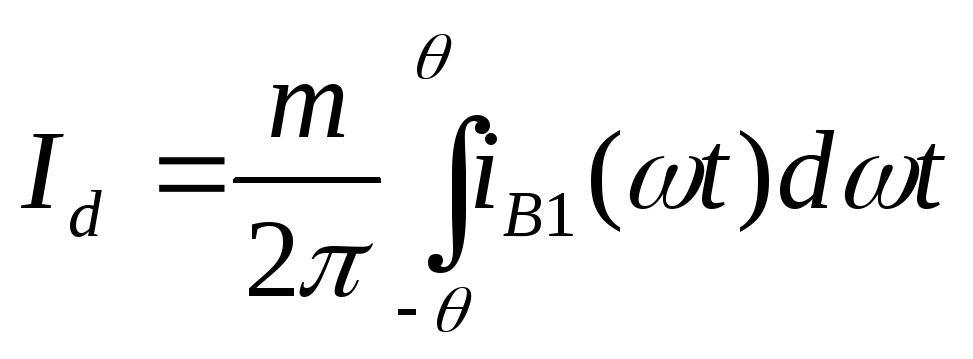 (2.10)
(2.10)
При углах 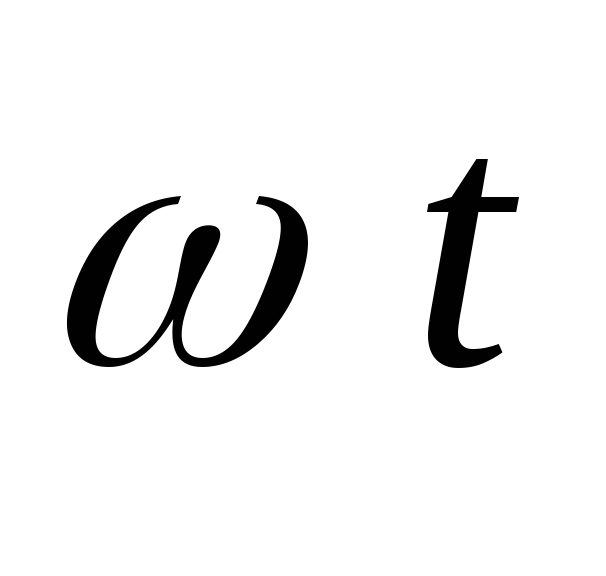 ,
равных
,
равных и
и ,
выпрямляемое переменное напряжение
,
выпрямляемое переменное напряжение ,
что позволяет записать:
,
что позволяет записать:
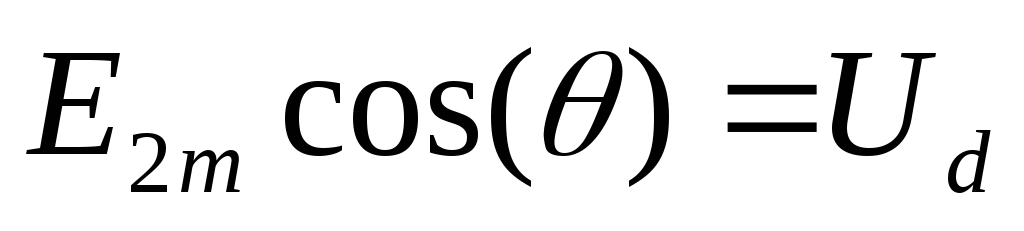 (2.11)
(2.11)
Следует отметить,
что в схеме Ларионова используется не
фазное напряжение, а линейное, поэтому
амплитудное напряжение фазы на вторичной
обмотке трансформатора будет в 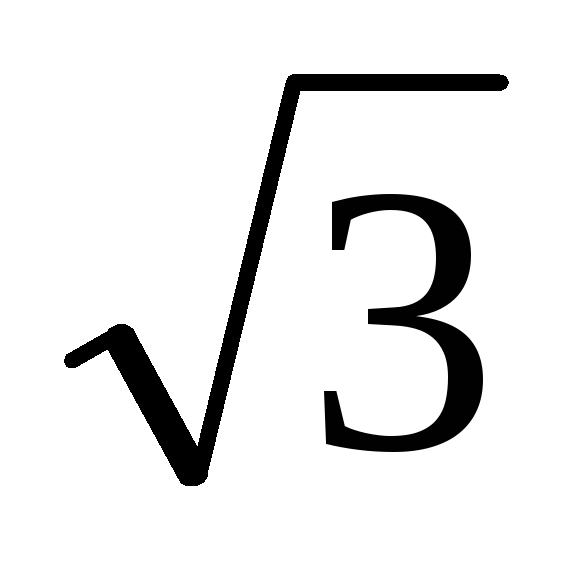 раз меньше
раз меньше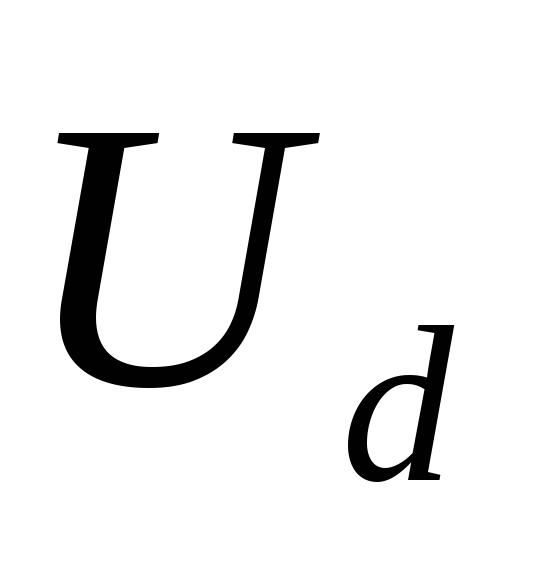 .
Максимум напряжения будет здесь не при
.
Максимум напряжения будет здесь не при ,
а при
,
а при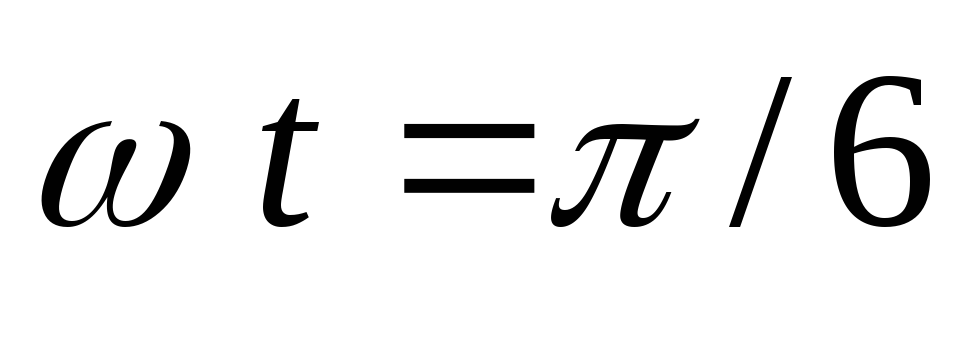 .
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
.
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
Произведя интегрирование (2.10), придем к выражению:
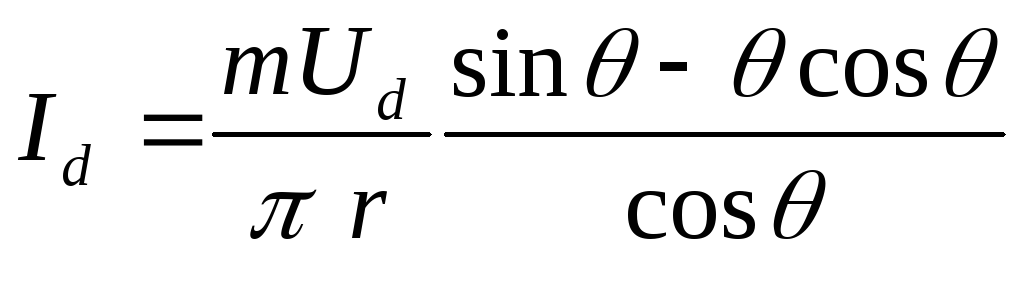 ,
(2.12)
,
(2.12)
связывающему
параметр режима работы выпрямителя  с выходным выпрямленным напряжением
с выходным выпрямленным напряжением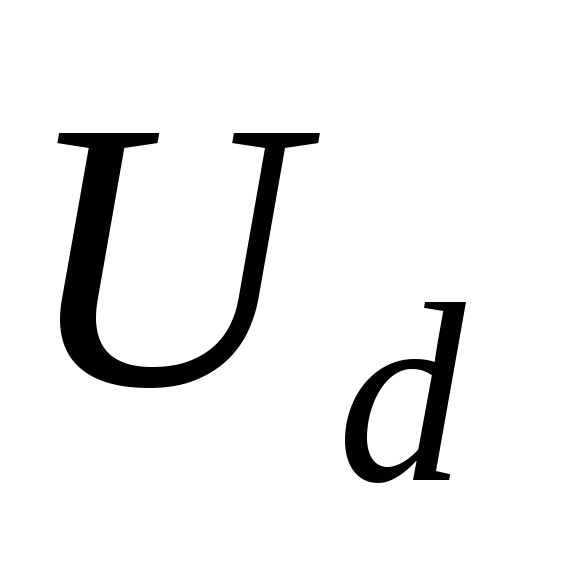 и током нагрузки
и током нагрузки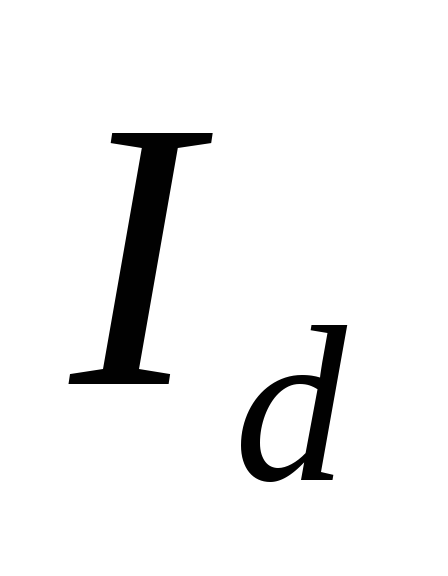 .
Обычно его записывают в несколько ином
виде [6 — 8]:
.
Обычно его записывают в несколько ином
виде [6 — 8]:
 или
или  . (2.13)
. (2.13)
В этом выражении
правая часть является однозначной
функцией угла
отсечки  .
.
Соотношение (2.13)
позволяет по выходным данным выпрямителя
(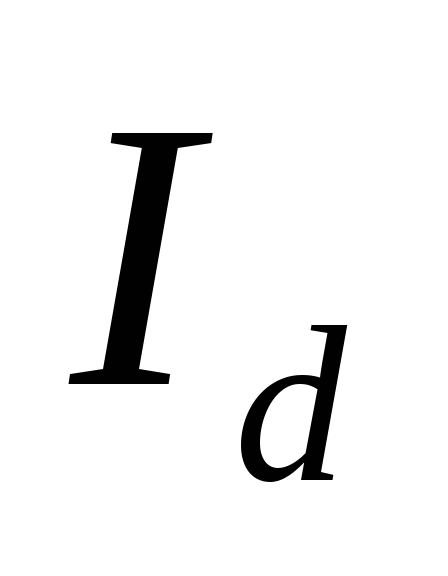 ,
,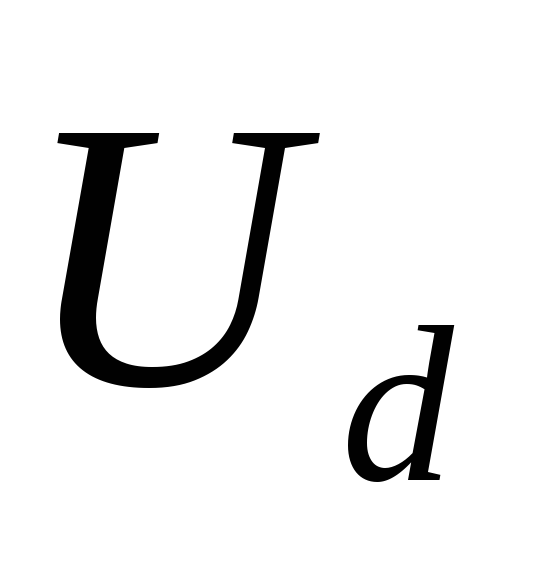 )
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки
)
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки  .
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
.
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
Действующее значение ЭДС вторичной обмотки, согласно (2.11) ,
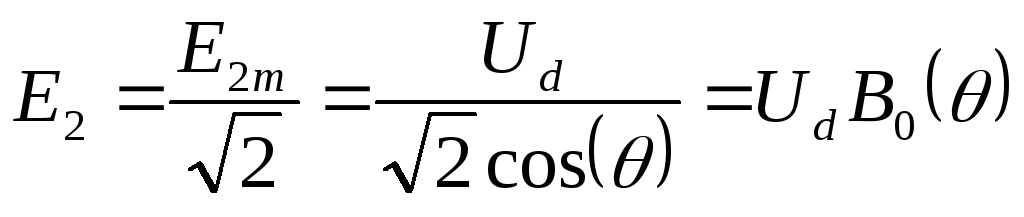 (2.14)
(2.14)
Действующее значение тока найдем по (2.9):
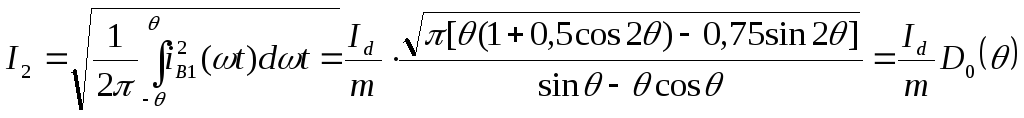 (2.15)
(2.15)
где
функция угла отсечки 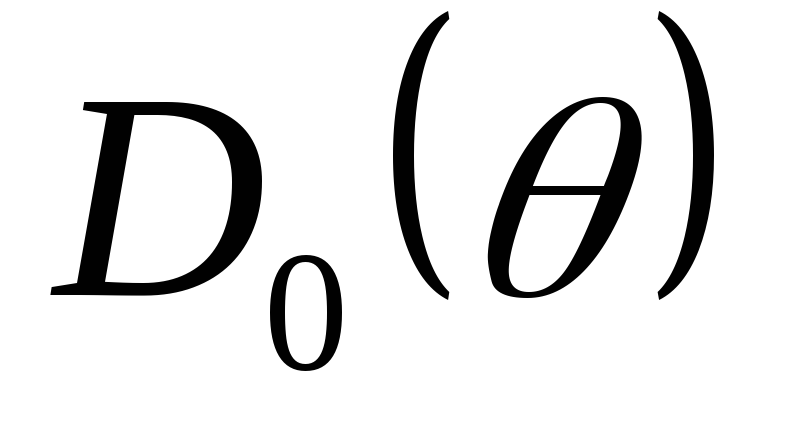 характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
Следует отметить,
что имеется разница в схемах между
действующим значением тока во вторичной
обмотке трансформатора 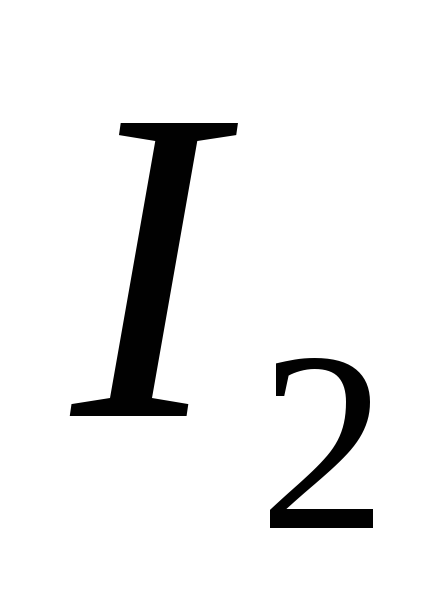 и током вентиля
и током вентиля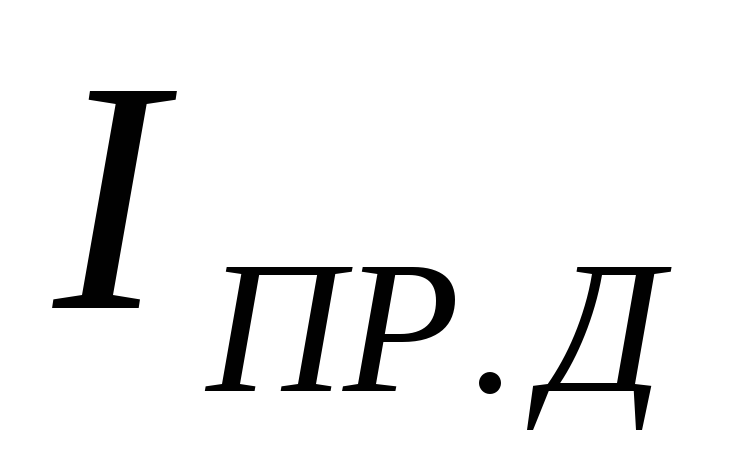 .
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
.
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
Максимального
значения ток вентиля достигает при 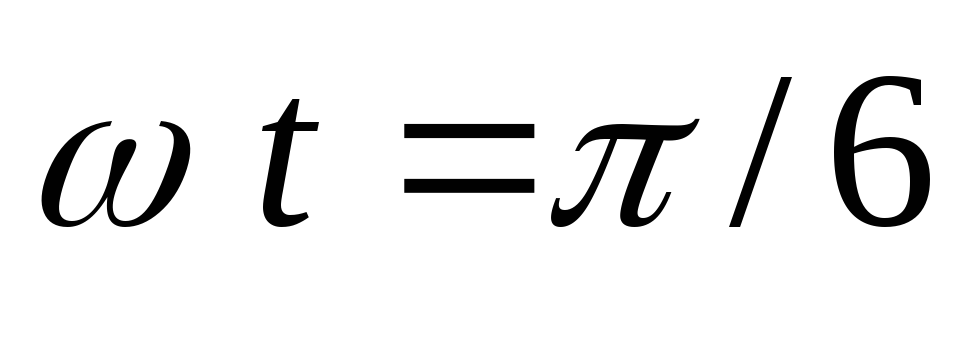 в схеме Ларионова и при
в схеме Ларионова и при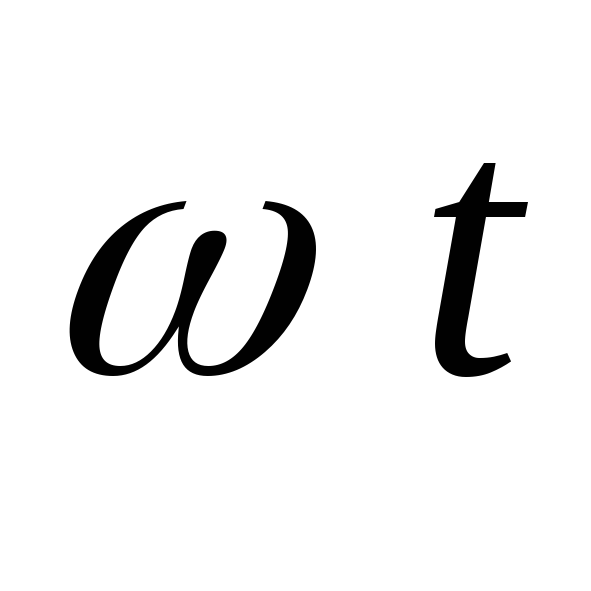 = 0 во всех остальных схемах:
= 0 во всех остальных схемах:
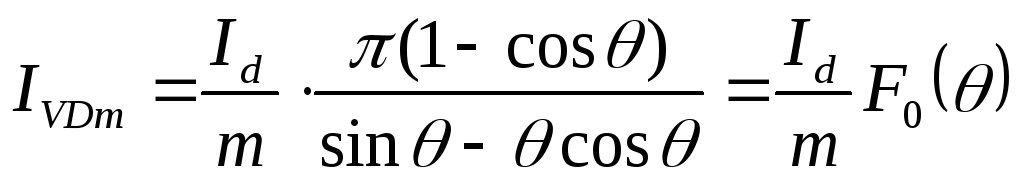 (2.16)
(2.16)
где 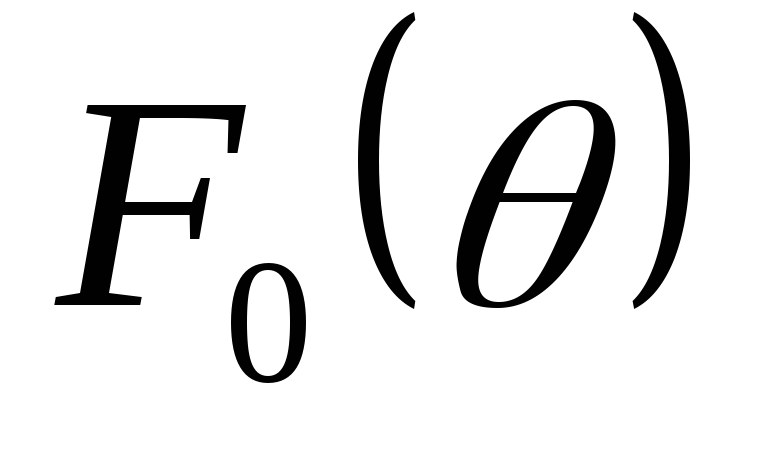 —
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
—
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
Трудность возникает
при расчете коэффициента пульсаций
выпрямителей, поскольку, положив 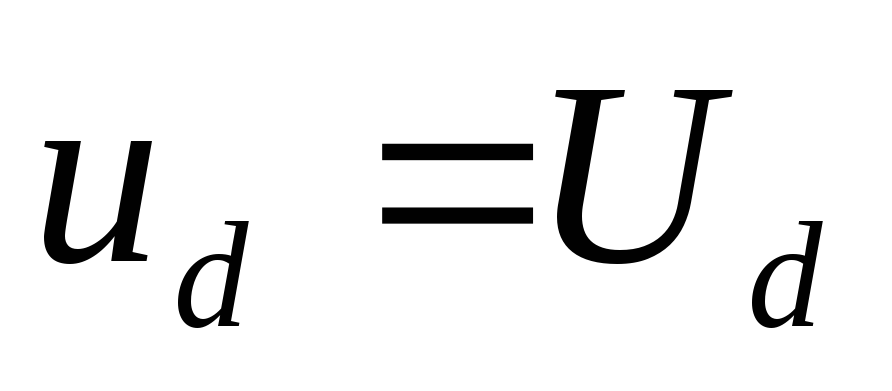 ,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
Таким образом,
общий ток всех вентилей представляет
собой совокупность импульсов тока,
определяемых (2.9) и следующих друг за
другом с интервалом 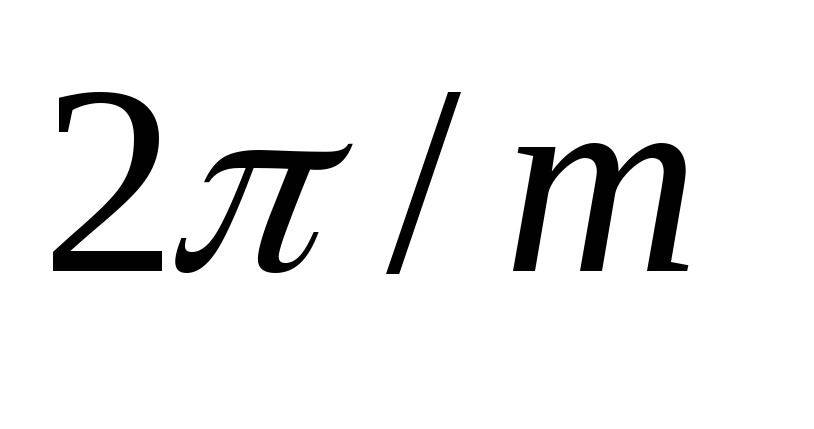 .
Амплитуда первой гармоники тока:
.
Амплитуда первой гармоники тока:
 (2.17)
(2.17)
Амплитуда первой гармоники напряжения:
 (2.18)
(2.18)
Коэффициент пульсаций по первой гармонике:
 (2.19)
(2.19)
где 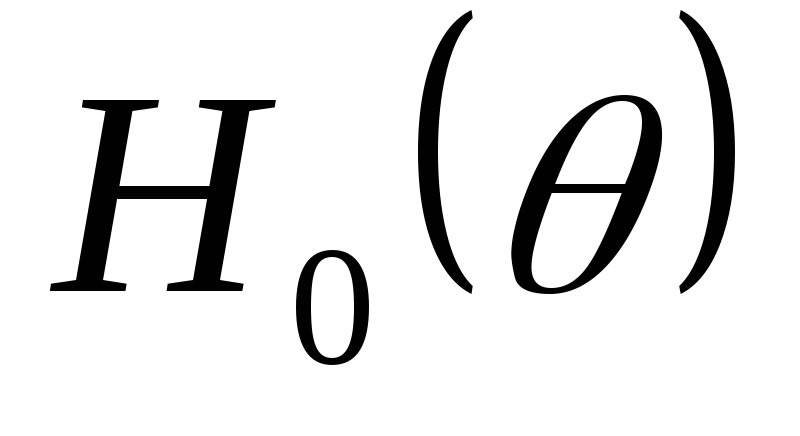 —
функция угла отсечки и числа фаз
выпрямителя.
—
функция угла отсечки и числа фаз
выпрямителя.
Данный
метод расчета из-за приближения 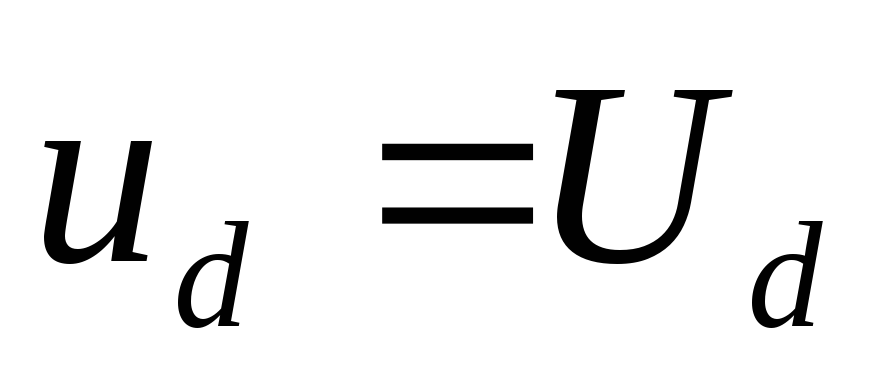 достаточно точен лишь при малых значениях
коэффициента пульсаций (
достаточно точен лишь при малых значениях
коэффициента пульсаций (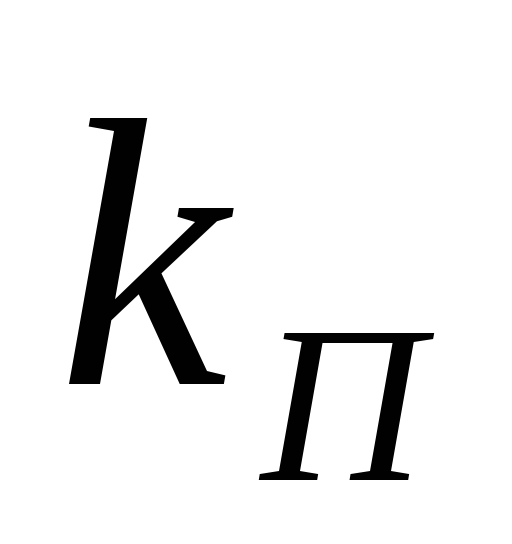 <0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что
<0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что >0,12,
то точность будет ниже требуемой (
>0,12,
то точность будет ниже требуемой (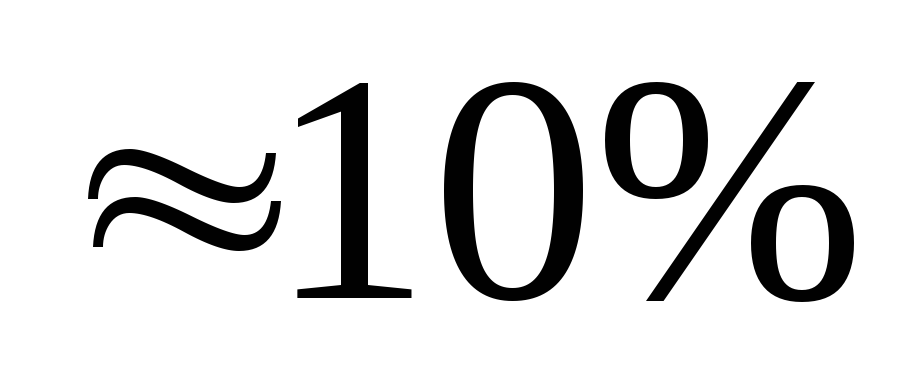 )
и возникнет необходимость изменения
расчетной модели.
)
и возникнет необходимость изменения
расчетной модели.
Самым простым
способом достижения требуемой точности
расчета является увеличение емкости
выходного конденсатора выпрямителя до
значения, которое обеспечивает выполнение
условия 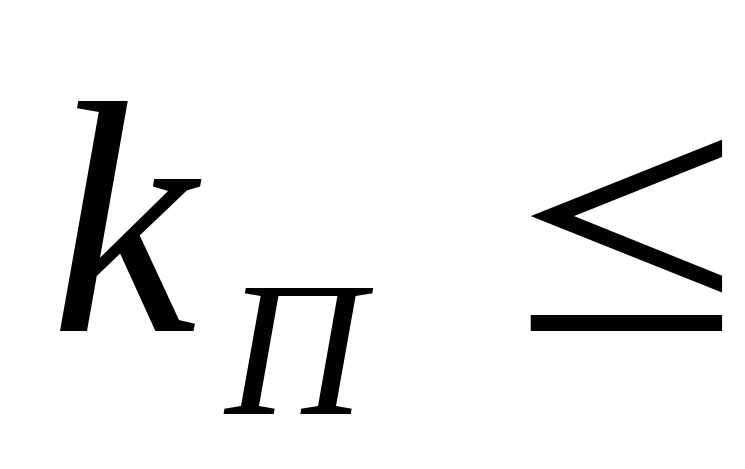 0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При
коэффициент пульсаций
0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При
коэффициент пульсаций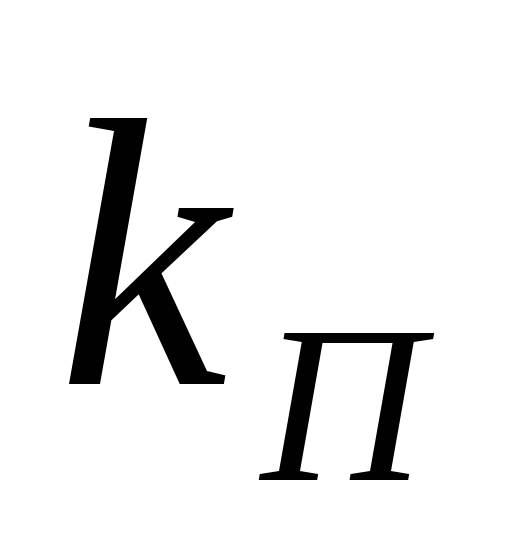 = 0,1.
= 0,1.
Недостатком
использования формулы (2.19) является то,
что о выполнении или нарушении условия
малости пульсаций узнают только в конце
расчета, когда определен угол отсечки  и найдена функция
и найдена функция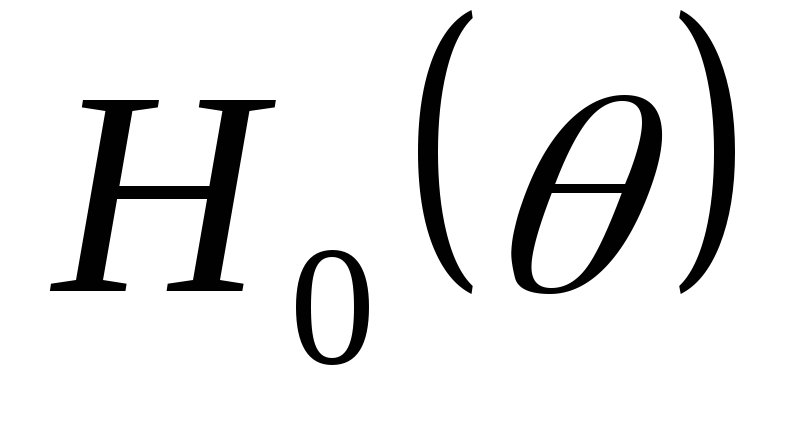 .
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость
.
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость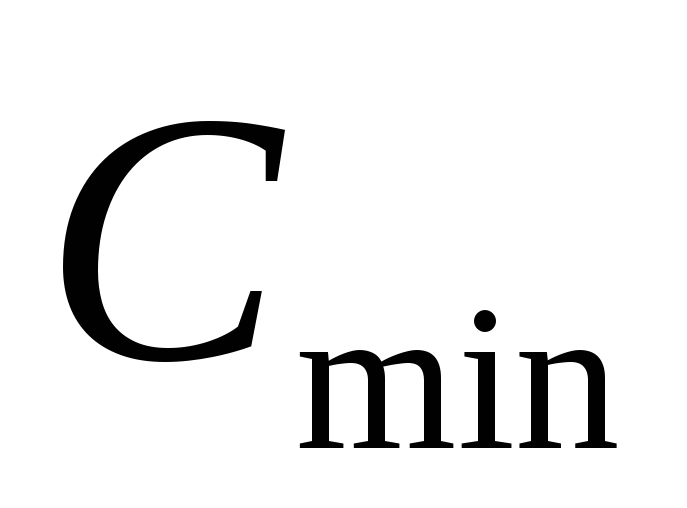 до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
Прийти к такому
соотношения можно представив зависимость 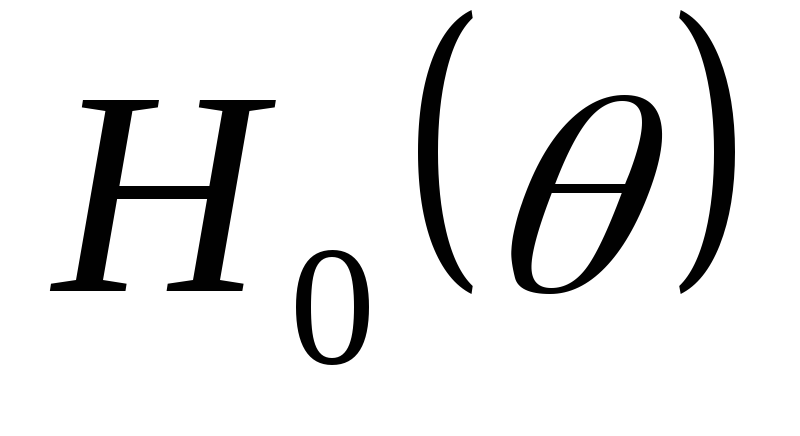 в приближенном виде. Так, для двухфазного
выпрямителя
в приближенном виде. Так, для двухфазного
выпрямителя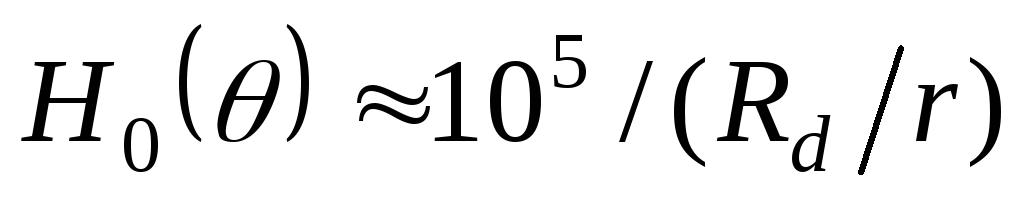 .
Подставив это приближение в (2.19), при
.
Подставив это приближение в (2.19), при = 0,1 получим:
= 0,1 получим:
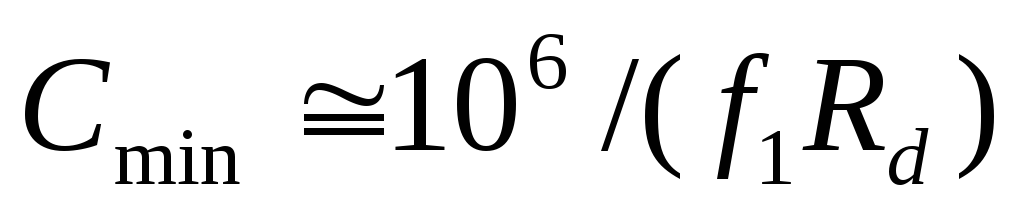 ,
(2.20)
,
(2.20)
где 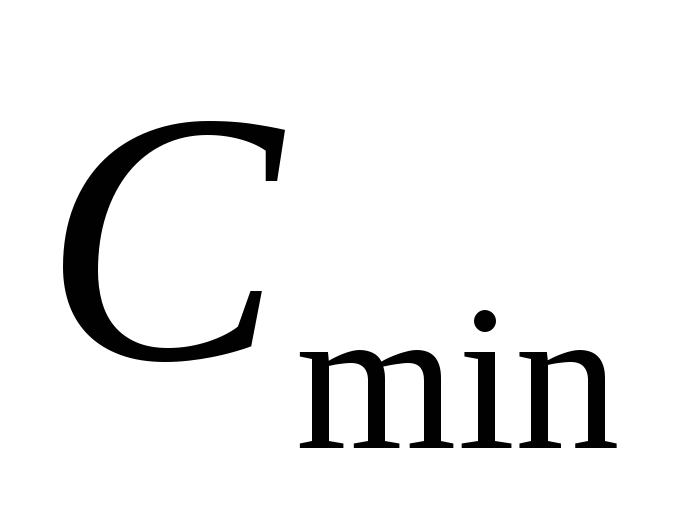 —
в мкФ.
—
в мкФ.
Таким образом, данный метод расчета выпрямителя заключается в проверке условия (2.20) с последующим определением режима работы по выражению (2.13) и нахождения расчетных показателей по формулам (2.14), (2.15), (2.16), (2.19).
Как было показано
ранее, выбранная модель (рис. 2.1, б)
достаточно проста, однако расчеты по
полученным на ее основе формулам дают
во многих случаях неплохую точность.
Вместе с тем в выпрямителях на относительно
высокие напряжения заметное влияние
на выходные показатели оказывает
индуктивность рассеяния трансформатора.
При ее учете придем к расчетной модели,
приведенной на рис. 2.4, а. Импульс тока
вентиля в такой модели заметно отличается
от косинусоидального (рис. 2.4, б) и имеет
длительность, большую 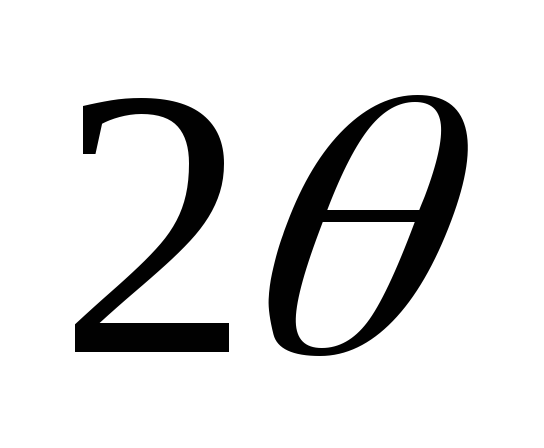 .
.
Проведя анализ
подобный ранее изложенному, получим
зависимости коэффициентов 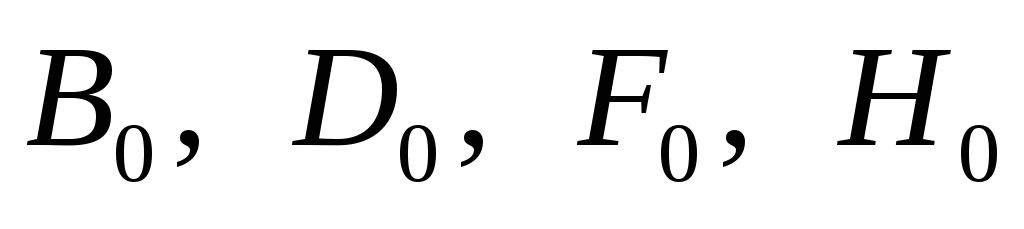 не только от угла
не только от угла ,
но и от относительного реактивного
сопротивления фазыx.
,
но и от относительного реактивного
сопротивления фазыx.
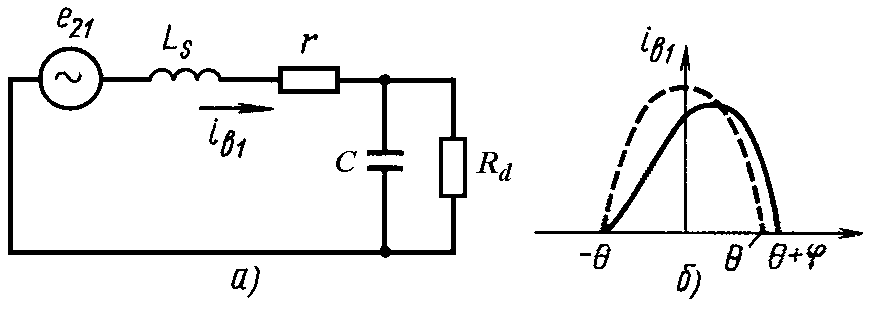
Рис. 2.4. Расчетная модель выпрямителя с учтенной индуктивностью
рассеяния (а) и кривые импульса тока вентиля в исходной и данной моделях (б).
Также может быть
определен тангенс угла  ,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
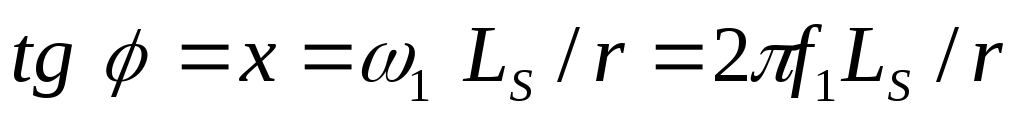 (2.21)
(2.21)
Найденные ранее
выражения для коэффициентов  соответствуют значению параметра
соответствуют значению параметра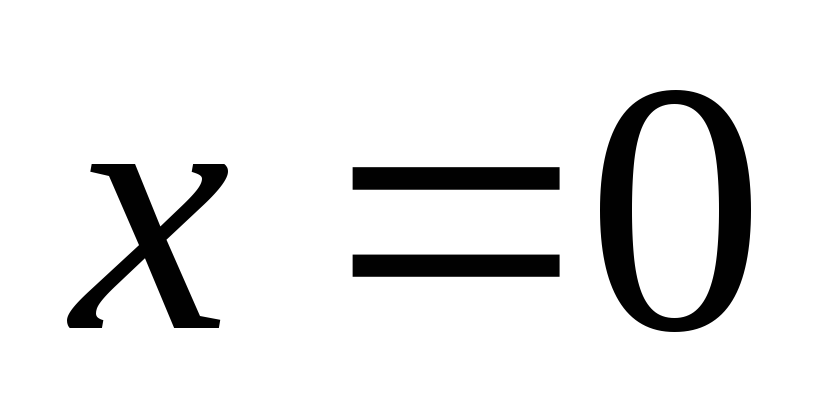 или
или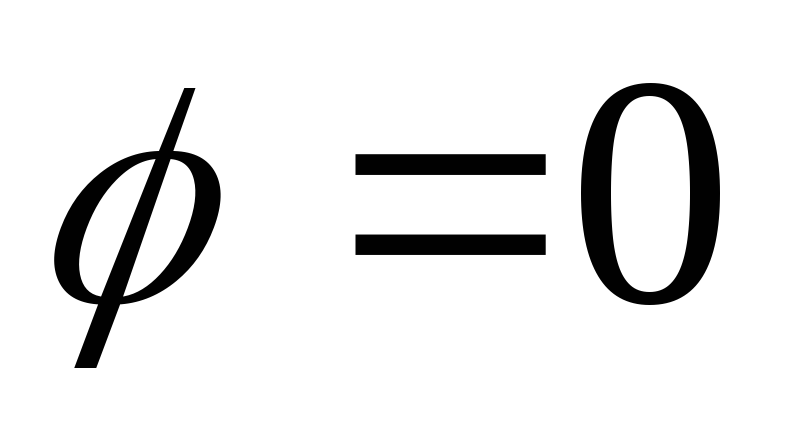 .
Зависимости коэффициентов
.
Зависимости коэффициентов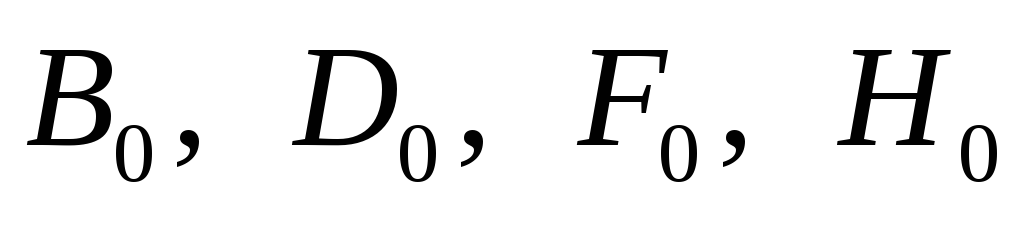 от функции параметра режима
от функции параметра режима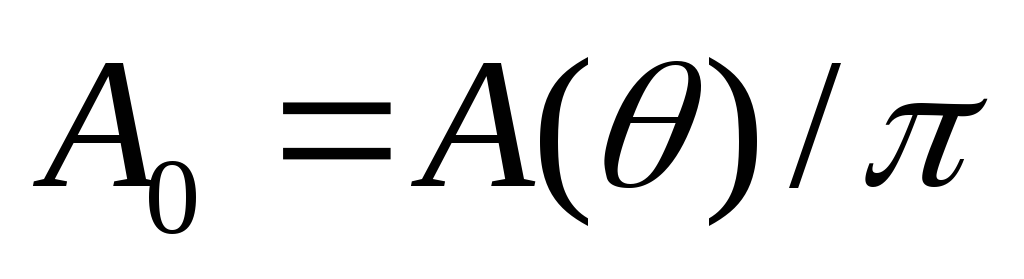 и угла
и угла приведены на рис. 2.5 — 2.9 [7, 8].
приведены на рис. 2.5 — 2.9 [7, 8].
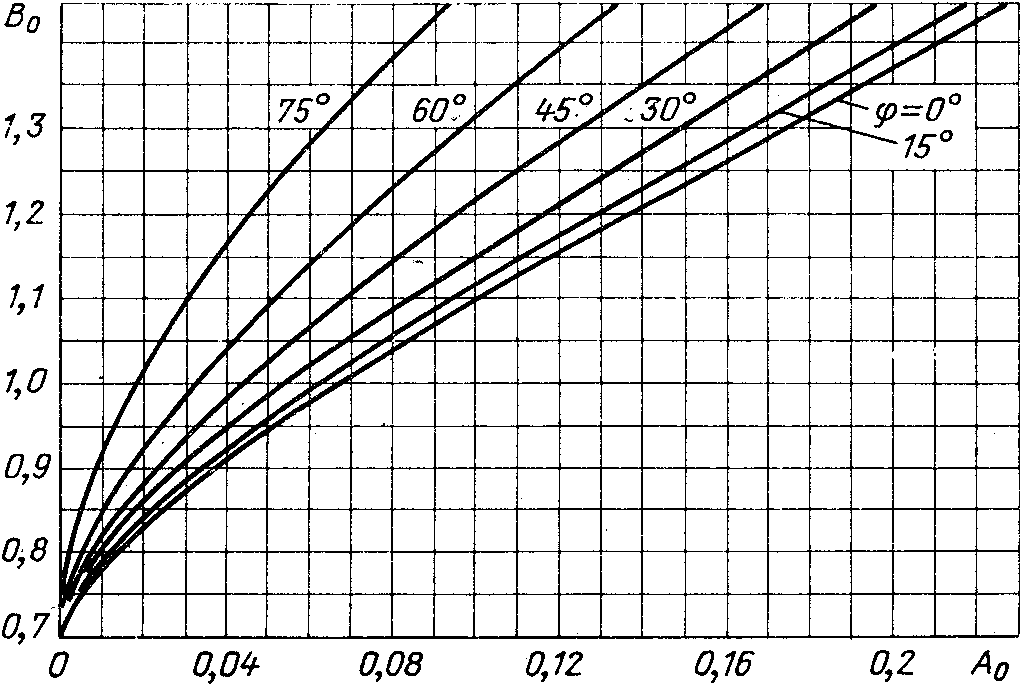
Рис.
2.5. Зависимость коэффициента 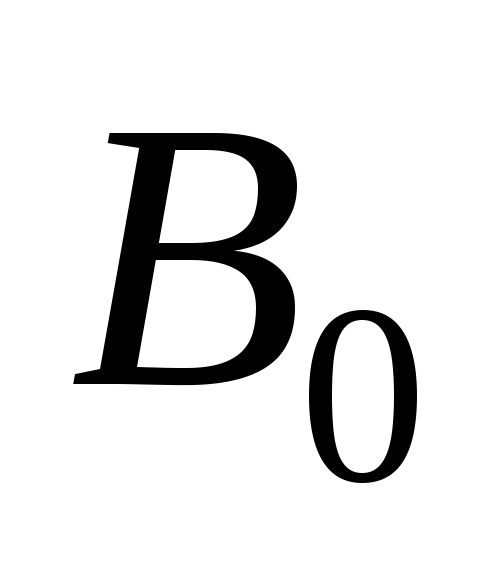 от
от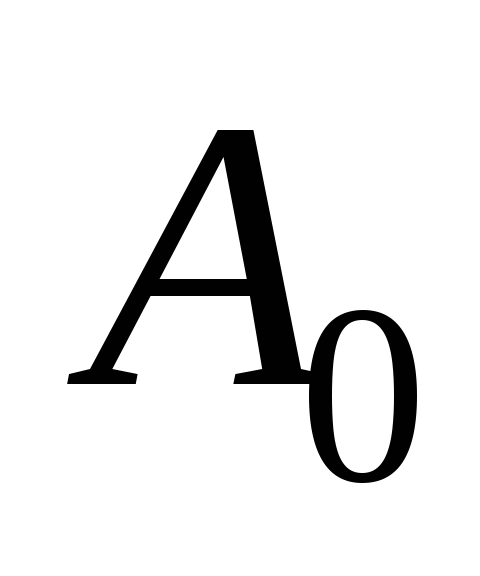 при различных значениях
при различных значениях .
.
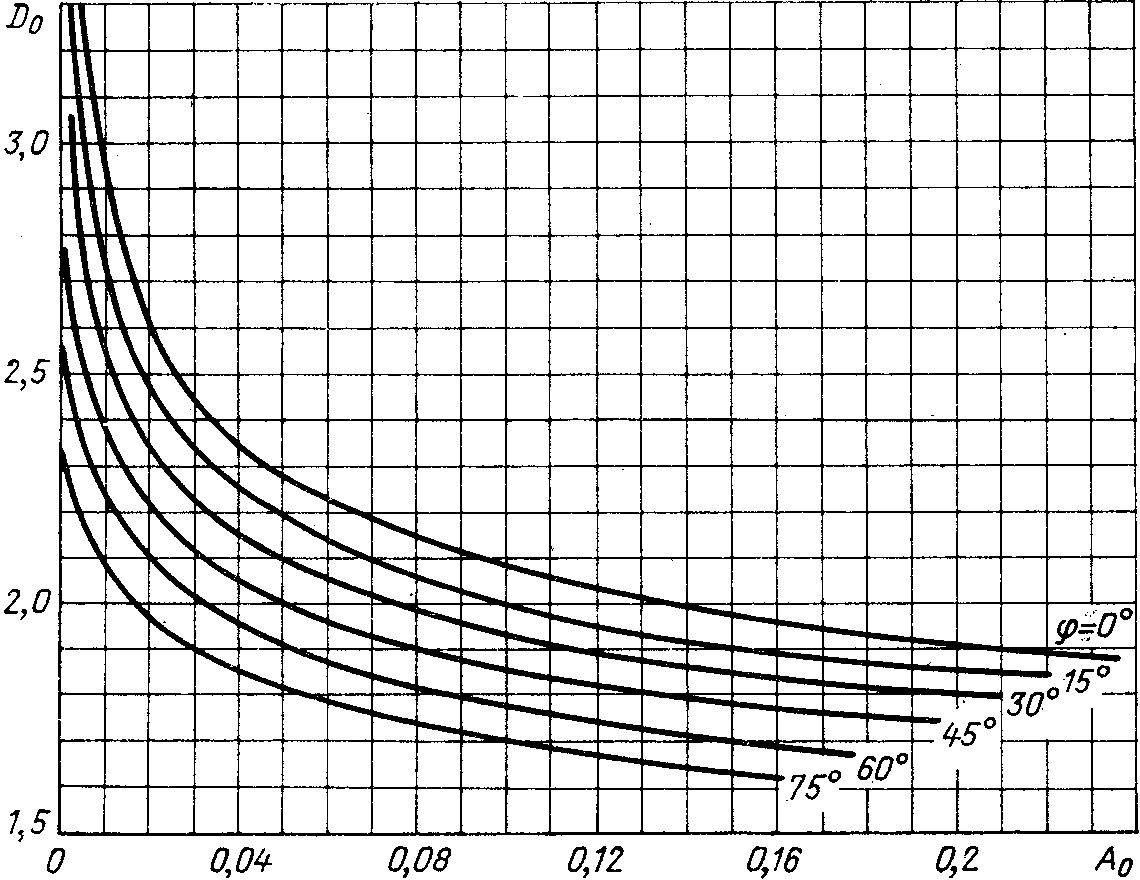
Рис.
2.6. Зависимость коэффициента 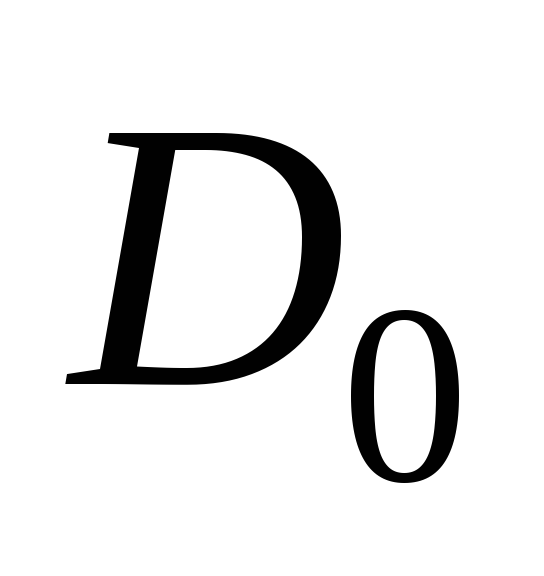 от
от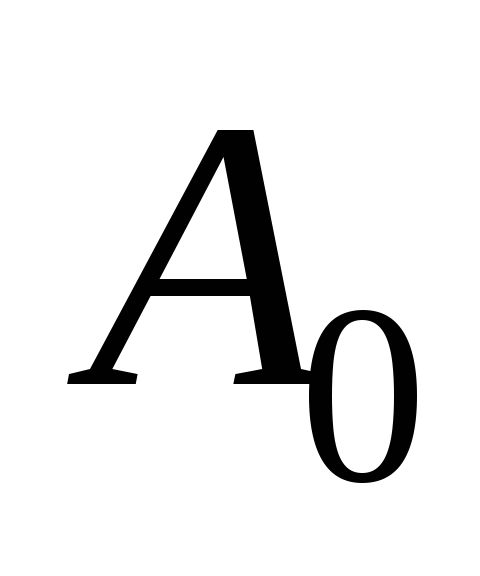 при различных значениях
при различных значениях .
.
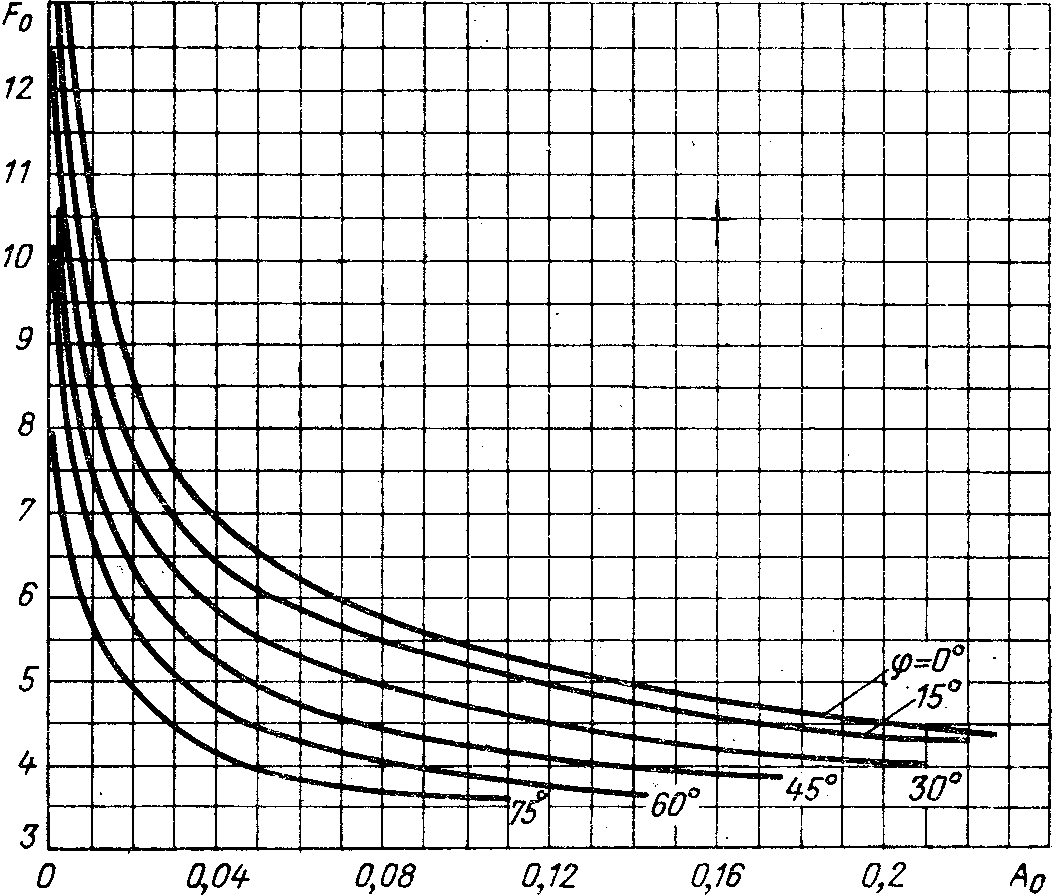
Рис.
2.7. Зависимость коэффициента
от при различных значениях
при различных значениях .
.
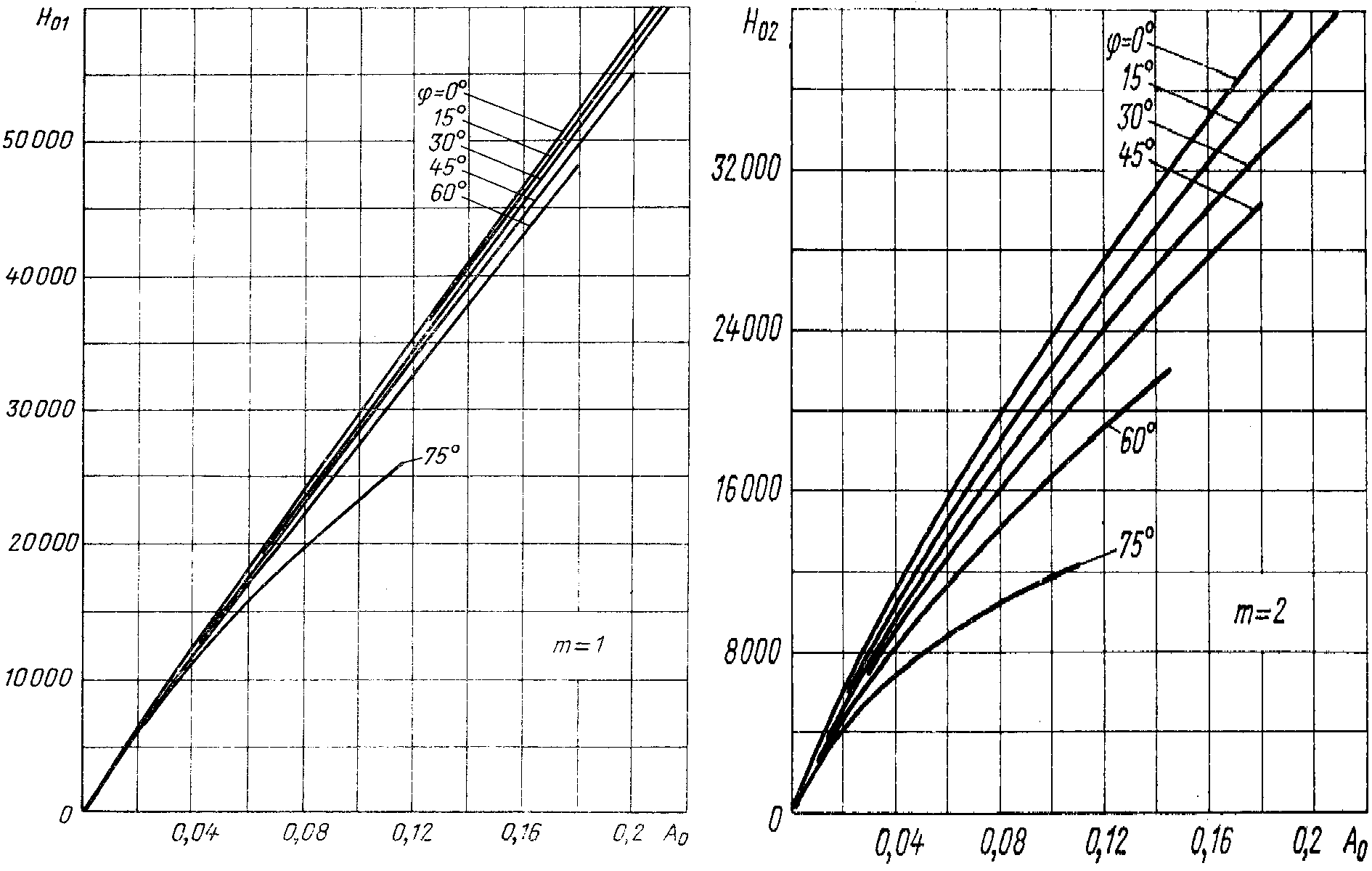
Рис.
2.8. Зависимости коэффициентов 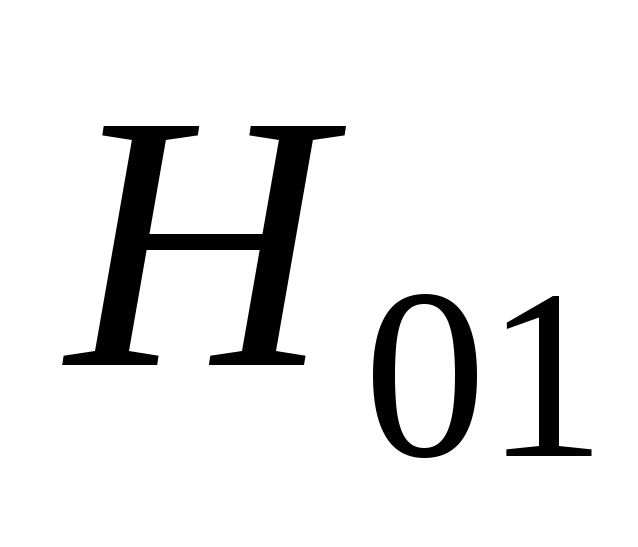 и
и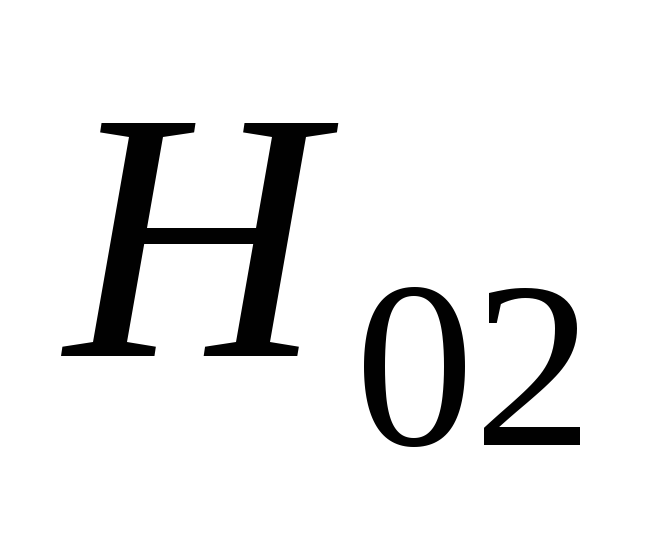 от
от и
и .
.

Рис.
2.9. Зависимости коэффициентов 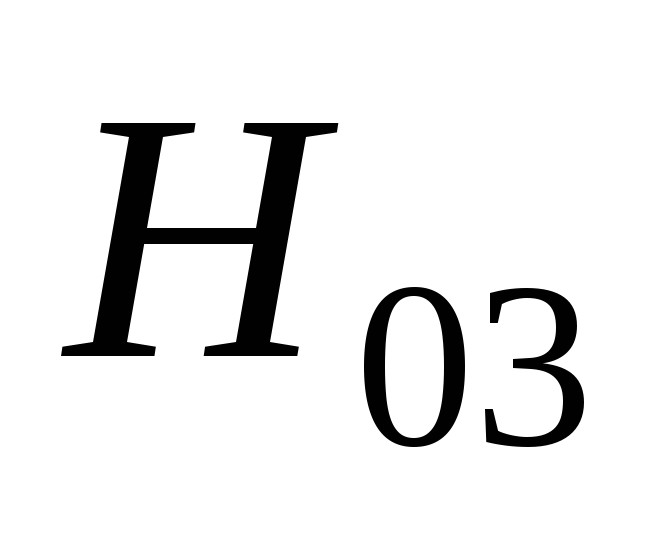 и
и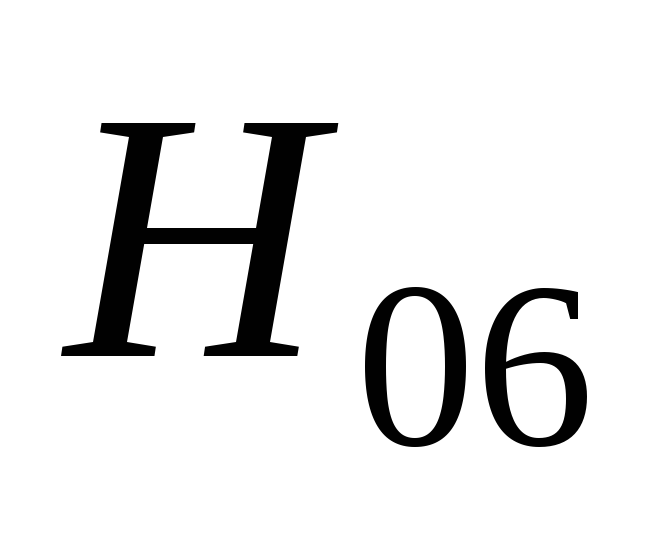 от
от и
и .
.
Действующий ток  первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
 (2.22)
(2.22)
и
действующий ток во вторичных обмотках
трансформатора  .
.
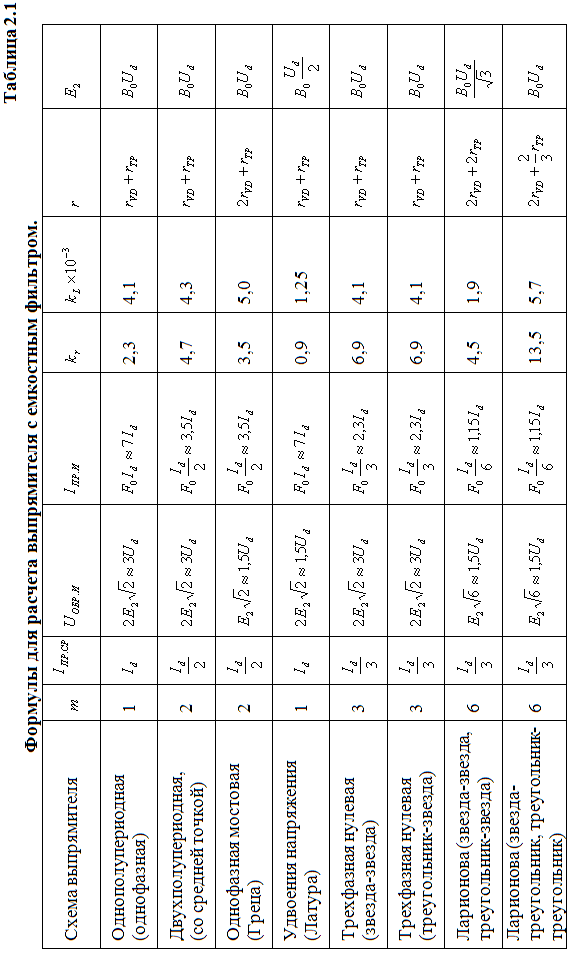
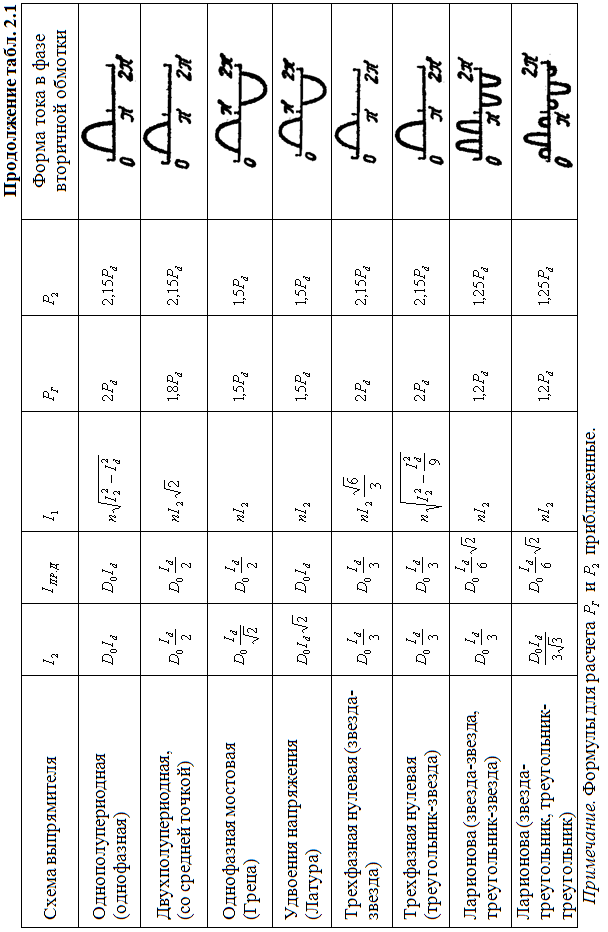
Габаритная мощность
трансформатора  определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
Таблица 2.2.
Схема | Габаритная мощность трансформатора |
Однополупериодная |
|
Мостовая | |
2-х полупериодная со средней точкой |
|
3-х фазная нулевая |
|
Ларионова |
Внешнюю (нагрузочную) характеристику выпрямителя, т.е. зависимость выпрямленного напряжения от тока нагрузки, рассчитывают по формуле [8]:
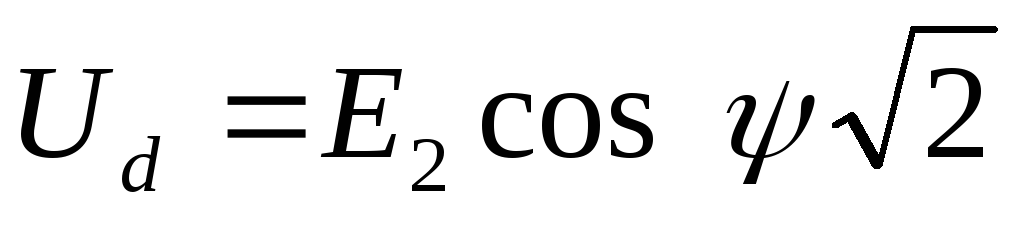 (2.23)
(2.23)
Задаваясь
различными значениями 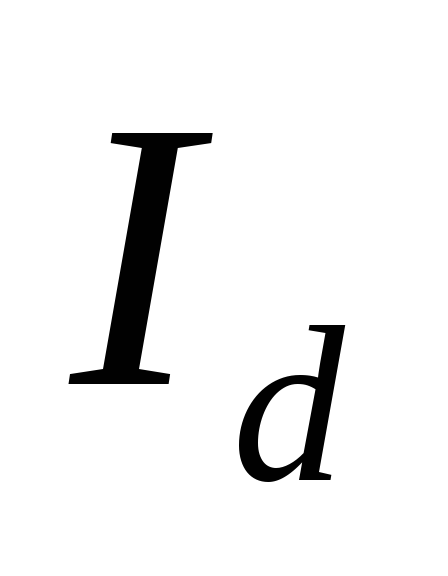 ,
определяют коэффициент
,
определяют коэффициент
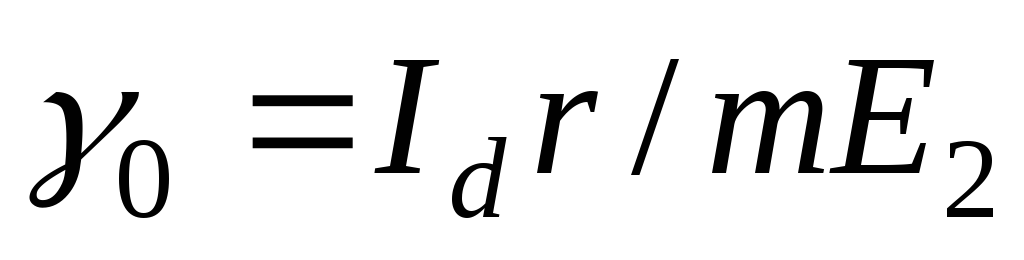 (2.24)
(2.24)
Значения  находят в зависимости от коэффициента
находят в зависимости от коэффициента и угла φ по графику на риc.
2.10 [8]. Подставляя величину
и угла φ по графику на риc.
2.10 [8]. Подставляя величину 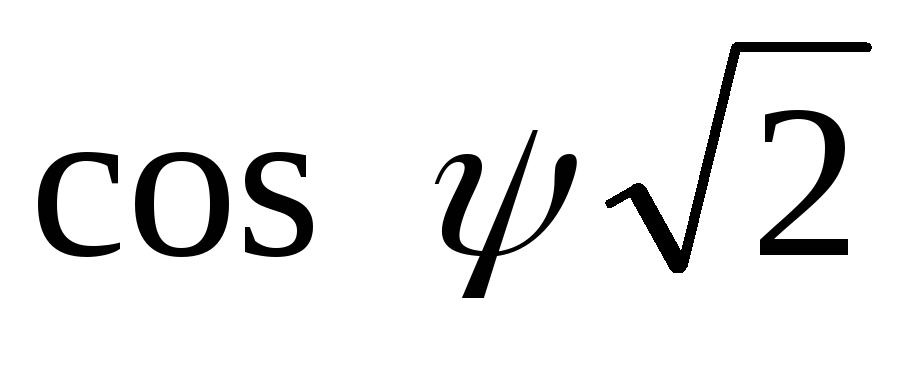 в формулу (2.23), находят
в формулу (2.23), находят для различных значений
для различных значений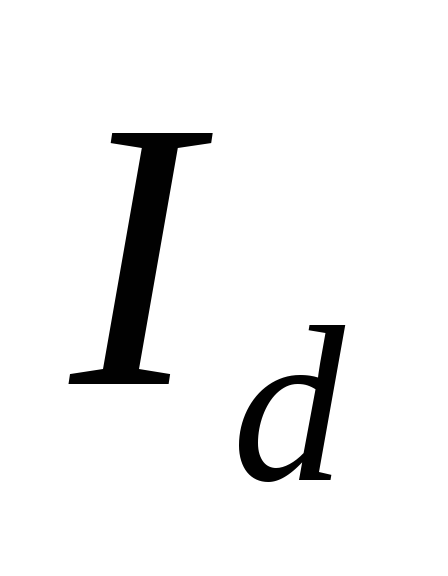 .
.
Напряжение на
конденсаторе будет равно напряжению
на нагрузке, но на случай отсоединения
нагрузки необходимо выбирать конденсатор
рассчитанный на напряжение
холостого хода выпрямителя – Uхх.
Очевидно, что при холостом ходе ( = 0)
= 0)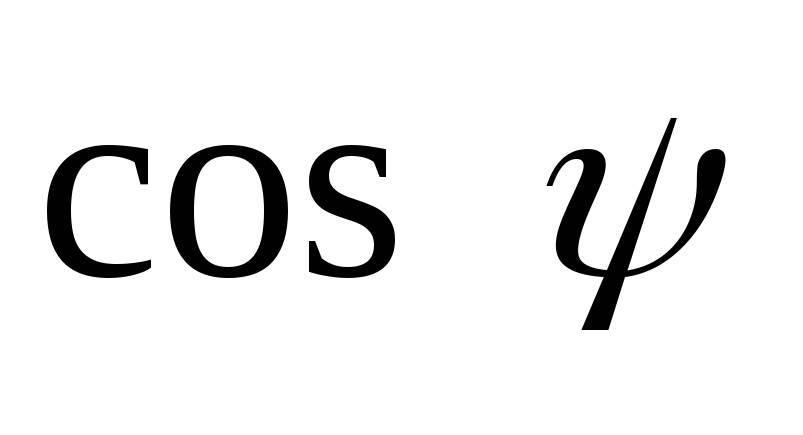 = 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
= 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
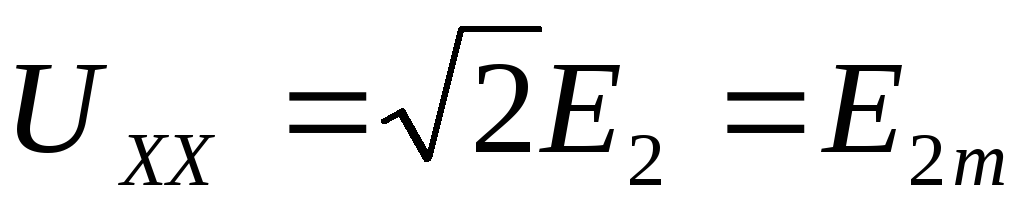 (2.25)
(2.25)
В схеме Ларионова при соединении вторичной обмотки в звезду:
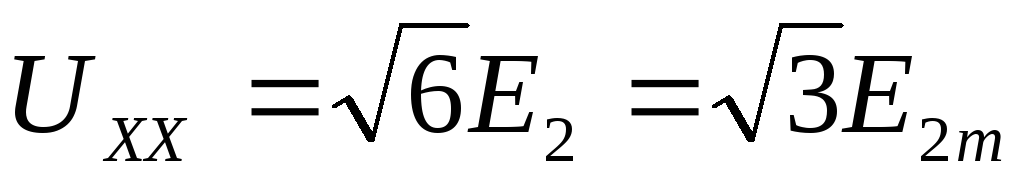 (2.26)
(2.26)
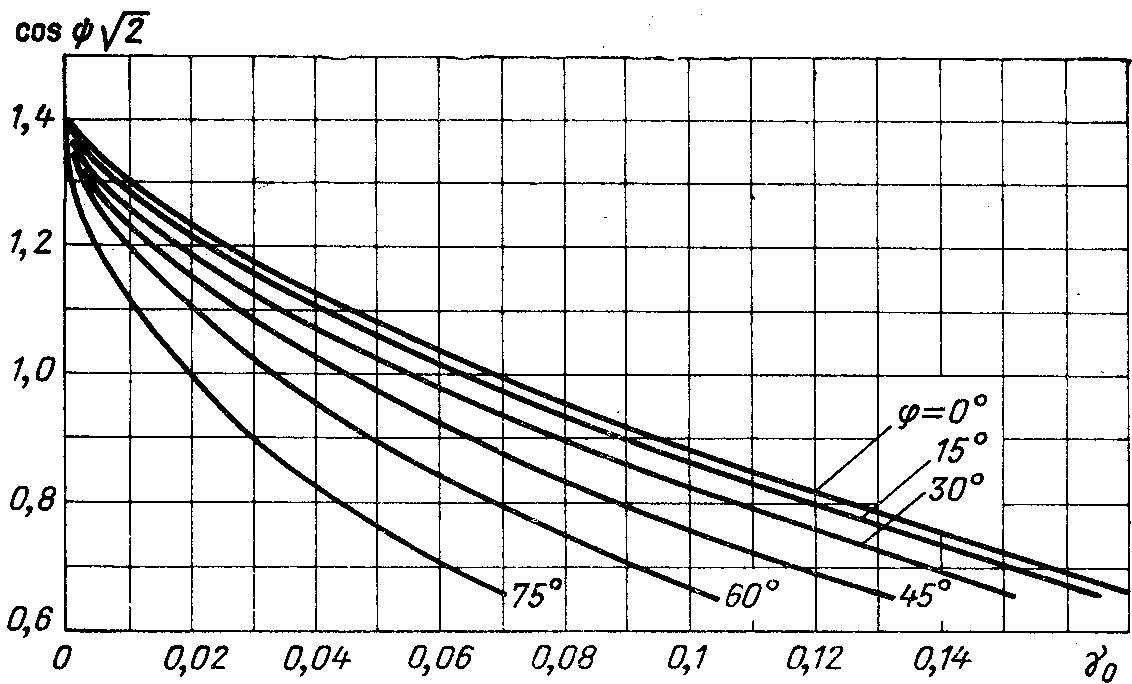
Рис.
2.10. Зависимость 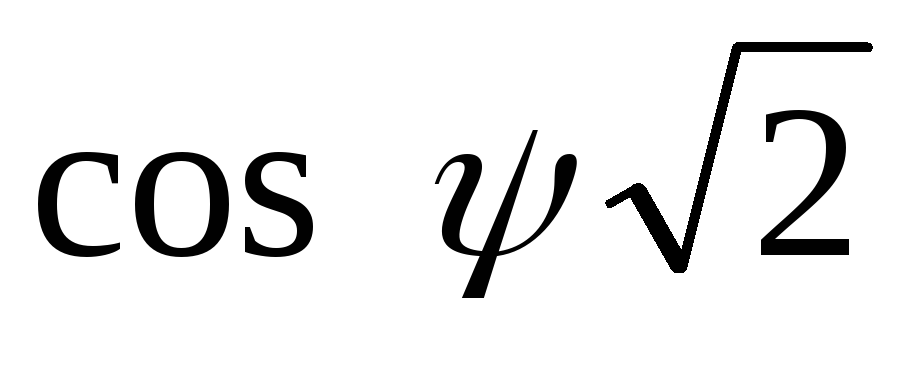 от коэффициента
от коэффициента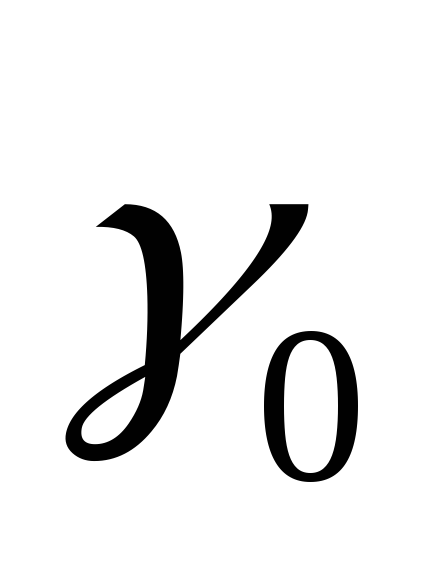
при различных значениях φ.
Учитывая то, что на фильтре знакопостоянное напряжение, конденсатор следует выбирать полярный, c номинальным напряжением не менее чем на 10% больше чем напряжение холостого хода выпрямителя (на случай скачков напряжения в электросети). Также следует учесть изменение емкости конденсатора в течение минимальной наработки, допустимое отклонение емкости, при этом допустимые напряжения переменной составляющей пульсирующего тока не должны превышать предельных значений для выбранного типа конденсатора. Переменная составляющая пульсирующего напряжения рассчитывается согласно (2.18). Поскольку допустимая переменная составляющая приводится в справочниках для частоты 50 Гц, ее следует пересчитать на частоту пульсаций напряжения на конденсаторе:
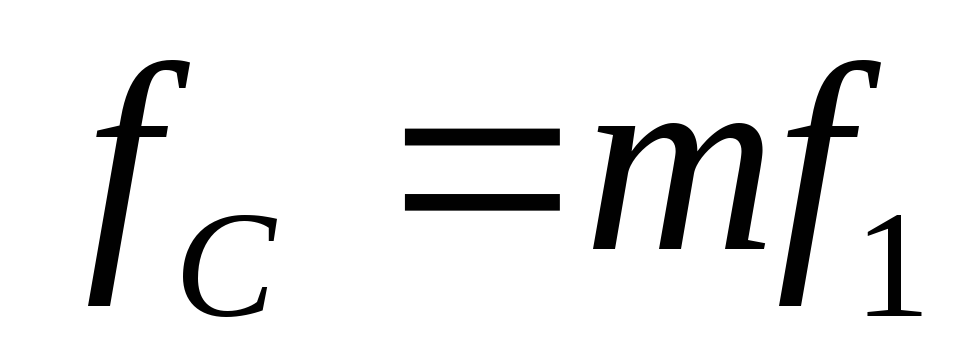 (2.27)
(2.27)
Приведенные соотношения получены для модели вентиля без порога выпрямления. Они обеспечивают хорошую точность расчета при выпрямленном напряжении более 15-20 В. При меньших значениях выпрямленного напряжения следует учитывать порог выпрямления [6].
ЭДС 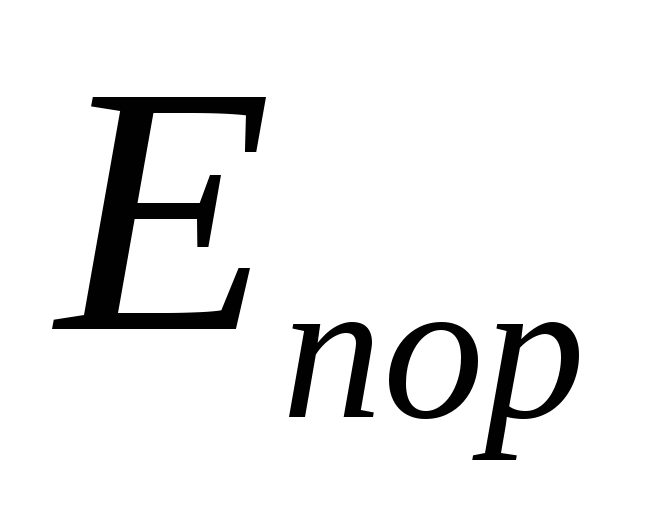 оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
Если считать напряжение:
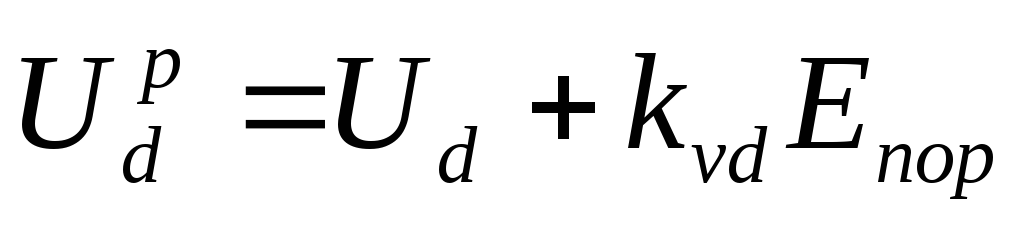 ,
(2.28)
,
(2.28)
которое
получается на выходном конденсаторе,
расчетным  и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения
и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения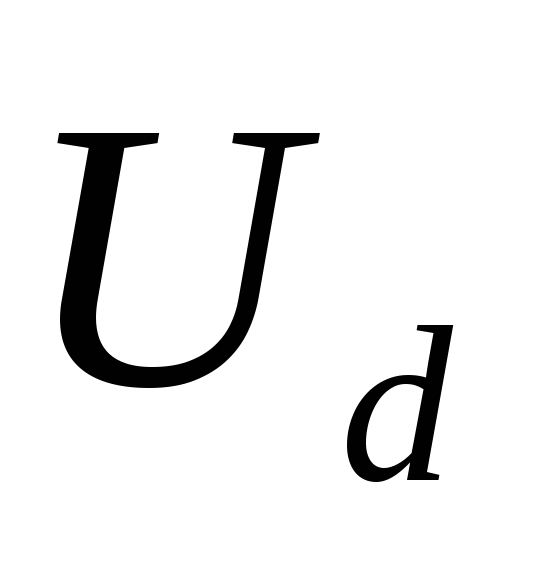 ,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент
,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент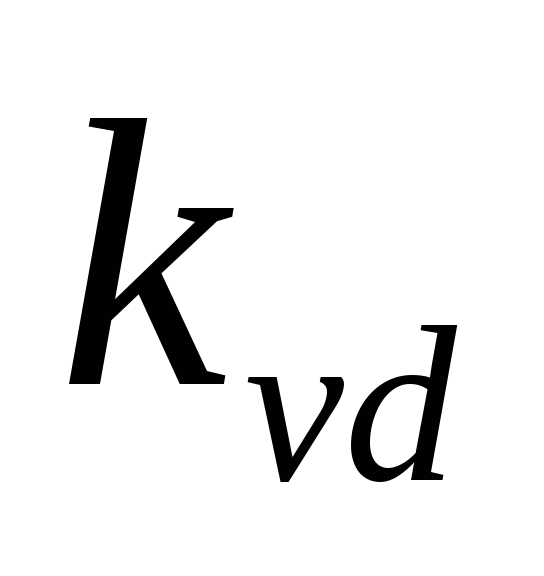 в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —
в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —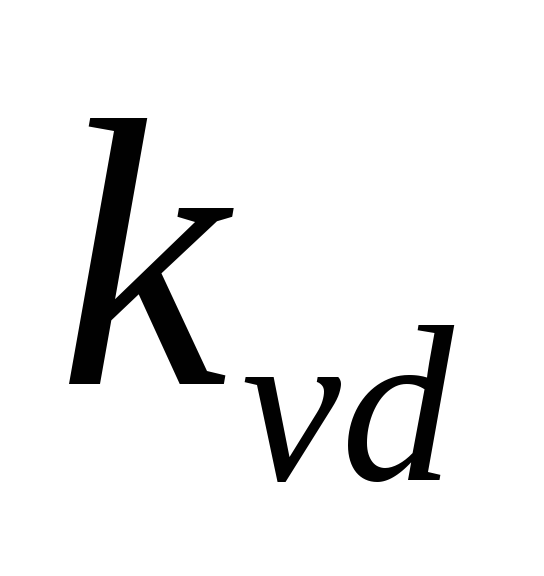 = 2, для остальных схем —
= 2, для остальных схем —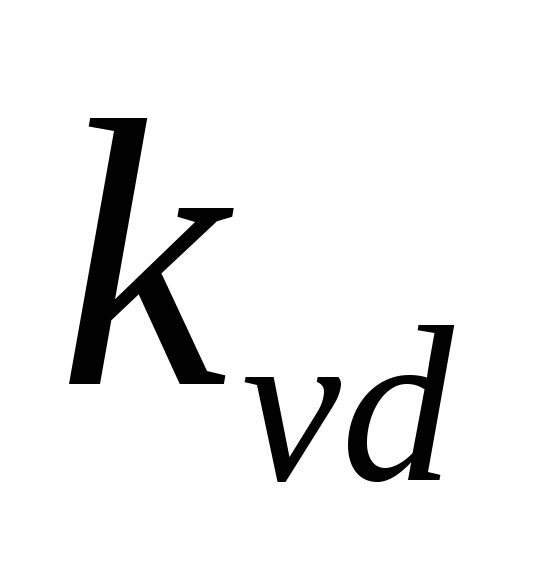 = 1.
= 1.
Расчет однофазных идеальных выпрямителей на активную нагрузку — Мегаобучалка
Екибастузский инженерно-технический институт
имени академика К.И. Сатпаева
| Кафедра: | Электроэнергетика |
«УТВЕРЖДАЮ»
проректор по учебной работе,
к.ф.-м.н., профессор
__________ Джандигулов А.Р.
«___»_____________200__ г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим работам
| по дисциплине: Силовые преобразовательные устройства |
| Специальность: | 050718 – Электроэнергетика |
| Форма обучения: | очная |
| Всего кредитов: | ||||
| Курс: | ||||
| Семестр: | ||||
| Лекции | часов | |||
| Практические | часов | |||
| Лабораторные | ||||
| СРСП | часов | |||
| СРС | часов | |||
| Трудоемкость | часов | |||
| Экзамен | семестр |
Екибастуз – 2008 г.
Рабочая программа составлена на основании рабочей учебной программы специальности 050718 – «Электроэнергетика»
Рабочую программу составил
| Старший преподаватель | Бексултанов А.Д. |
(должность, звание) (подпись) (Фамилия И.О.)
Рабочая программа рассмотрена на заседании кафедры
| «Электроэнергетика» |
Протокол №_1_ «_18_» ___09_______ 2008_ г.
| Заведующий кафедрой: Доцент | Полищук В.И. |
Одобрена учебно-методическим советом инженерного факультета
Протокол №_ от______ 200_ г.
| Председатель: к.т.н., профессор | Саржанов К.Б. |
Одобрена учебным отделом
| Начальник | Бирюкова Л.Ф. |
Офис: ул. Энергетиков, 54, ауд.№ 103
Тел: 8 (7187) 33 — 05 – 53 (вн. 109)
Е- mail: [email protected]
Содержание
| Практическая работа №1. Расчет однофазных идеальных выпрямителей на активную нагрузку | |
| Практическая работа №2. Расчет однофазных выпрямителей (собранных по нулевой схеме) | |
| Практическая работа №3. Задачи по работе выпрямителей на активно-индуктивную нагрузку | |
| Практическая работа №4. Расчет трехфазного мостового неуправляемого выпрямителя на активную нагрузку | |
| Практическая работа №5. Рассчитать управляемый выпрямитель | |
| Практическая работа №6 Расчет трехфазного управляемого выпрямителя с нулевой точкой и нулевым диодом | |
| Практическая работа №7 Трехфазный симметричный управляемый мост | |
| Практическая работа №8 Расчет однофазного выпрямителя работающего на встречную ЭДС (противо-ЭДС) | |
| Практическая работа №9 Однофазный инвертор, ведомый сетью | |
| Практическая работа №10 Рассчитать трехфазного мостового выпрямителя, работающего на активную нагрузку с емкостным фильтром | |
| Практическая работа № 11 Рассчитать параметры сглаживающего Г-образного LC-фильтра, установленного на выходе трехфазного выпрямителя с нулевой точкой | |
| Практическая работа № 12 Расчитать трехфазный мостовой выпрямитель |
Практическая работа № 1
Расчет однофазных идеальных выпрямителей на активную нагрузку
Задание: Рассчитать однофазный мостовой выпрямитель, работающий на активную нагрузку по следующим исходным данным и нарисовать временные диаграммы основных токов и напряжений.
Действующее значение напряжения на вторичной обмотке трансформатора В.
Сопротивление нагрузке Ом.
Потери в выпрямителе отсутствуют.
Методика решения задачи
Формализуем исходные данные.
Дано:
Схема – однофазная мостовая.
Элементы схемы – идеальны.
В,
Ом.
, , , , , , , , , , , , , — ?
Временные диаграммы основных токов и напряжений — ?
1. Рассчитать выпрямитель — это значит найти все перечисленные величины, которые обозначают соответственно:
, — среднее значение выпрямленного напряжения и тока;
— мощность выпрямленного тока;
— коэффициент трансформации;
, — действующие значения токов первичной и вторичной обмоток;
, , — габаритная (типовая) мощность соответственно первичной, вторичной обмоток и трансформатора в целом;
, , — ток вентиля (диода, тиристора) — соответственно среднее значение, действующее значение и максимальное.
— обратное максимальное напряжение, прикладываемое к вентилю.
— потери мощности на вентиле.
2. Прежде чем перейти к решению задачи, заметим, что не все указанные величины можно найти, потому что не задано напряжение на первичной обмотке. В связи с этим возможны два варианта решения задачи:
— доопределить задачу, задавая, например, В, 50 Гц;
— исключить из определенных величин те, которые определить невозможно (в нашем случае это , ).
Выбираем первый вариант, т.е. доопределяем задачу.
3. По словесному описанию идентифицируем схему, если она не приведена в исходных данных, и обозначим все токи и напряжения так, как представлено на рис. 1.
Рис. 1
4. Дальнейшее решение задачи возможно двумя способами:
4.1. Табличным, воспользовавшись для этого таблицей «Расчетные соотношения для выпрямительных схем» (см. приложение 1).
4.2. Аналитическим, воспользовавшись выведенными в теории выражениями.
Выберем табличный способ решения.
5. В таблице находим схему однофазную мостовую (схема Греца), работающую на активную нагрузку, для идеального (без потерь) выпрямителя и далее находим необходимые величины.
6. Выпрямленное напряжение из соотношения
Þ В.
7. Выпрямленный ток (среднее значение)
А.
8. Мощность выпрямленного тока
Вт.
9. Коэффициент трансформации
.
10. Действующее значение тока вторичной обмотки трансформатора найдем из табличного соотношения
Þ А.
11. Действующее значение тока первичной обмотки трансформатора из таблицы
Þ А.
12. Габаритные мощности первичной и вторичной обмоток трансформатора для мостовой схемы
Þ
ВА.
Рассчитанных данных достаточно, чтобы выбрать подходящий трансформатор по каталогу или составить техническое задание на его проектирование.
13. Для выбора диодов выпрямителя рассчитаем максимальное обратное напряжение, которое прикладывается к выключенному диоду
Þ В.
Допустимое обратное напряжение, которое должен выдержать диод, выбирается с некоторым запасом:
,
где — некоторый коэффициент запаса по напряжению, причем меньшее значение берется для более надежного преобразователя.
14. Среднее значение тока диода:
Þ А.
15. Действующее значение тока вентиля (диода):
Þ А.
16. Максимальное значение тока вентиля:
Þ А.
17. Потери мощности в одном диоде:
,
где , — параметры аппроксимированной ВАХ, соответственно остаточное падение напряжения (при нулевом токе) и динамическое сопротивление диода в рабочей точке. В данном случае диоды идеальны — =0; =0.
18. Далее из той же таблицы берем другие параметры выпрямителя, которые понадобятся нам, например, при выборе фильтра.
Число пульсаций напряжения на периоде сети .
Частота первой гармоники Гц.
Коэффициент пульсаций выпрямленного напряжения по первой гармонике
.
Временные диаграммы основных токов и напряжений, к которым относятся , , , , , , , представлены на рис. 3.9.
Рис. 3.9
Их построение должно вестись в следующей последовательности:
18.1. Нам известно, что действующее значение напряжения на вторичной обмотке 200 В. При этом мы дополнили задачу и конкретизировали, что первичное напряжение – напряжение промышленной сети 220В, 50 Гц. Форма напряжения сети синусоидальная. С него и начнем наши построения, задавшись масштабом по оси ординат и абсцисс. Для удобства построения полупериод синусоиды делим на 6 равных частей (30 электрических градусов).
18.2. На первом полупериоде, когда напряжение положительно, проводят ток вентилей В1 и В4. Так как нагрузка активная, то форма тока будет повторять форму напряжения (синусоида) с амплитудой А. Аналогично для вентилей В2 и В3 на втором полупериоде.
18.3. Мгновенное значение выпрямленного тока нагрузки будет равно сумме токов вентилей и . Среднее значение выпрямленного тока равно 18 А (прямая линия).
18.4. Ток вторичной обмотки трансформатора численно будет равен току вентилей, но на первом полупериоде он будет положительный, а на втором – отрицательный.
18.5. Мгновенное значение выпрямленного напряжения численно равно напряжению вторичной обмотки, но оно будет однополярное. Среднее значение выпрямленного напряжения будет постоянным и численно равно 180 В.
18.6. Напряжение, которое прикладывается к вентилям В1, В4, на первом полупериоде равно нулю (вентили В1, В4 включены), на втором полупериоде равно напряжению вторичной обмотки и приложено к вентилям В1, В4 в обратном (выключающем) направлении, так как на втором полупериоде включены вентили В2 и В3. Напряжение на В2 и В3 будет иметь такую же форму, но будет сдвинуто на один полупериод.
Задание на СРСП
| Параметры | варианты | |||||||||
| , В | ||||||||||
| , Ом | 0,5 | 1,0 | 3,0 | 6,0 | 3,0 | |||||
| , В | ||||||||||
| , Ом | 2,0 | 4,0 | 0,6 | 0,9 | 1,5 |
Практическая работа № 2
Расчет однофазных выпрямителей (собранных по нулевой схеме)
Рассчитать и сравнить однофазный выпрямитель со средней точкой и однофазный однополупериодный выпрямитель, работающие на активную нагрузку без фильтра, если выпрямленное напряжение на нагрузке равно 180 В, мощность постоянного тока в нагрузке равно 3240 Вт, напряжение питающей сети 220 В, частота сети 50 Гц.
1. Формулируем исходные данные:
Дано:
Схема – однофазная со средней точкой (нулевая) и однофазная однополупериодная.
Вт;
В;
В;
Гц.
__
Определить , , , , , , , , , , , ,
, .
2. Схемы выпрямителей представлены на рис. 1.
б)
а)
Рис.1
3. Определяем выпрямленный ток (среднее значение) из равенства
Þ
А.
4. Определяем сопротивление нагрузки
Ом.
5. Замечаем, что по выходным параметрам , , , рассчитываемые выпрямители полностью идентичны мостовому, рассмотренному в практической работе №1, что позволит корректно сравнить все выпрямители между собой.
6. Расчет выпрямителей проведем также табличным способом, выбирая из таблицы приложения 4.2 нужную схему, нагрузку и строку — идеальный выпрямитель (коэффициенты в скобках).
7. Для однофазного нулевого выпрямителя (со средней точкой):
Þ В.
Þ А.
Þ А.
.
Þ А.
Þ ВА.
Þ ВА.
Þ ВА.
Þ В.
Þ А.
Þ А.
Þ А.
8. Для однофазного однополупериодного выпрямителя:
Þ В.
Þ А.
Þ А.
.
Þ А.
Þ ВА.
Þ ВА.
ВА.
Þ В.
Þ А.
Þ А.
Þ А.
9. Сравнение произведем таблично.
Из таблицы видно, что при одной и той же мощности в нагрузке требуемая мощность трансформатора в мостовой схеме минимальна 3986 ВА, а в однополупериодной схеме выпрямителя мощность – 10012 ВА. Число вентилей в мостовой схеме – 4, в нулевой – 2, в однополупериодной – 1. Обратное напряжение, прикладываемое к вентилю, в мостовой 283 В, а в нулевой и однополупериодной – 565 В. Максимальный ток вентиля в мостовой и нулевой – 28,3 А, а в однополупериодной – 56,5 А.
| Выпрямитель Параметр | Мостовой | Со средней точкой | Однополупериодный |
| [B] | |||
| [А] | |||
| [Bт] | |||
| [B] | |||
| [А] | 20,0 | 14,1 | 28,3 |
| 1,1 | 1,1 | 0,55 | |
| [А] | - | ||
| [А] | 18,2 | 18,2 | 39,6 |
| [ВА] | |||
| [ВА] | |||
| [ВА] | |||
| [В] | |||
| [А] | 14,1 | 14,1 | 28,3 |
| [А] | 28,3 | 28,3 | 56,5 |
| [А] |
| Параметры | варианты | |||||||||
| Pd, Вт | ||||||||||
| U1, В | ||||||||||
| , В | ||||||||||
| Pd, Вт | ||||||||||
| U1, В | ||||||||||
| , В |
2.3 Расчет неуправляемых выпрямителей с ёмкостным фильтром
2.3.1. Расчет однофазного выпрямителя. [17] При анализе процессов в выпрямителях с С-фильтром (рис. 2.24) сопротивления соединительных проводов, питающей сети и диодов выпрямителя принимаются равными нулю.
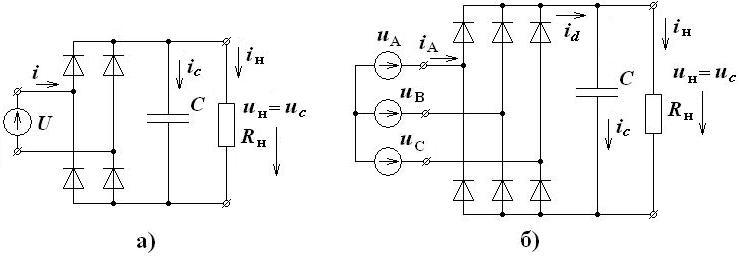
Рисунок 2.24– Двухполупериодные выпрямители
На рис. 2.25 приведены временные диаграммы напряжений и токов в характерных участках схемы однофазного выпрямителя.

Рисунок 2.25 – Временные диаграммы напряжений и токов однофазного выпрямителя
Коэффициент пульсации (Кп) напряжения на выходе выпрямителя определяется как отношение половины изменения напряжения на конденсаторе DUC /2 (рис.2.25, а) к среднему значению напряжения на нагрузке Ud , т.е.
 .
(2.7)
.
(2.7)
Так как UCmax = Um и принимая во внимание (2.7), среднее напряжение и ток на выходе выпрямителя определяются выражениями:
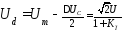 ,
(2.8)
,
(2.8)
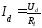 .. (2.9)
.. (2.9)
При этом
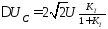 .
(2.10)
.
(2.10)
Диод выпрямителя начинает пропускать ток в момент, когда мгновенное значение сетевого напряжения превысит величину напряжения на конденсаторе, определяемом углом отсечки q1 (рис. 2.25, а), который определяется из выражения:
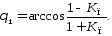 (2.11)
(2.11)
Путём несложных преобразований получается выражение для расчета емкости конденсатора фильтра:
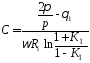 .
(2.12)
.
(2.12)
Максимальное значение анодного тока, достигаемое в момент q1, равно
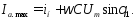 (2.13)
(2.13)
Среднее значение тока вентиля:
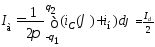 (2.14)
(2.14)
Действующее значение тока:
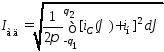 . (2.15)
. (2.15)
Несмотря на наличие ряда допущений точность расчета достаточно высока, как правило, она выше точности исходных данных и стабильности параметров компонентов.
Рассматриваемое устройство является цепью первого порядка и, в соответствии с относительной постоянной времени CRН = const, можно осуществить выбор основных параметров выпрямителя с С-фильтром по таблице 2.3.
Таблица 2.3
КП | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,10 | 0,11 | 0,12 |
СRН | 147 | 71,5 | 46,6 | 32,8 | 27,0 | 22,1 | 18,7 | 16,2 | 14,2 | 12,6 | 11,3 | 10,3 |
Ud/U | 1,4 | 1,39 | 1,37 | 1,36 | 1,35 | 1,33 | 1,32 | 1,31 | 1,30 | 1,29 | 1,27 | 1,26 |
Iamax/Id | 30,4 | 21,2 | 17,1 | 14,7 | 13,1 | 11,9 | 10,9 | 10,1 | 9,5 | 9,0 | 8,5 | 8,1 |
Ia/Id | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 |
Ia.д/Id | 3,2 | 2,7 | 2,4 | 2,2 | 2,1 | 2,0 | 1,92 | 1,96 | 1,8 | 1,75 | 1,71 | 1,67 |
IС.д/Id | 4,4 | 3,64 | 3,2 | 2,99 | 2,8 | 2,65 | 2,53 | 2,43 | 2,34 | 2,27 | 2,2 | 2,14 |
Cos | 0,99 | 0,98 | 0,97 | 0,97 | 0,96 | 0,95 | 0,95 | 0,94 | 0,93 | 0,93 | 0,92 | 0,92 |
| 0,33 | 0,39 | 0,43 | 0,46 | 0,48 | 0,51 | 0,53 | 0,54 | 0,56 | 0,58 | 0,59 | 0,62 |
| 0,33 | 0,38 | 0,42 | 0,44 | 0,46 | 0,48 | 0,5 | 0,51 | 0,52 | 0,53 | 0,54 | 0,55 |
Данные таблицы показывают, что повышение требований к качеству выходного напряжения выпрямителя связано с существенным ростом амплитуды тока (при рассмотренных значениях коэффициента пульсаций амплитуда тока превышает его среднее значение в 16… 60 раз).
Пример . Требуется рассчитать однофазный мостовой выпрямитель с С- фильтром со следующими исходными данными:
номинальные напряжения U= 220 В;
частота питающего напряжения f =50 Гц;
коэффициент пульсаций Кп = 0,12;
сопротивление нагрузки Rн=117 Ом.
Определяем угол q1, используя расчетное соотношение (2.11):
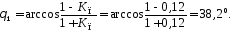
По формуле (2.14) рассчитываем величину емкости, обеспечивающую заданный коэффициент пульсации на нагрузке:
 .
.
Среднее значение напряжения и тока на нагрузке определяем по (2.8) и (2.9), соответственно:
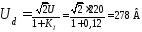 ,
, 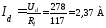 .
.
Максимальное значение анодного тока находим по соотношению (2.13):
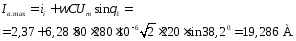
Среднее значение анодного тока находим по (2.14)
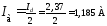 .
.
Действующее значение тока диода определяем по (2.15)
 .
.
2.3.2. Расчет трёхфазного выпрямителя. Схема трехфазного мостового выпрямителя с емкостным фильтром приведена на рис. 2.24 б. Устройство может работать в режиме непрерывного тока, который наблюдается при большой мощности нагрузки, либо в режиме прерывистого тока, который проявляется при снижении мощности. Электромагнитные процессы в режиме прерывистого тока не имеют принципиальных отличий от работы однофазного выпрямителя и для расчета можно использовать выражения (2.7…2.15) при подстановке в них пульсности трехфазного мостового выпрямителя p=6. В качестве сетевого берется линейное напряжение: U=Uл. Максимальное напряжение на конденсаторе равно:
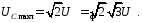
В режиме непрерывного тока Ud= 2,34U, q1 = q2 = 30°.
Принятые при расчете допущения для трехфазного выпрямителя оказываются достаточно грубыми, в частности, нельзя принять малым значение угла 2. Поэтому результаты расчета следует уточнить, проведя последовательные итерации при определении емкости фильтра. Уточненные данные для расчета трехфазного выпрямителя приведены в табл. 2.4.
Таблица 2.4 — Расчётные соотношения для трёхфазной мостовой схемы
КП | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,067 | 0,067 | 0,067 |
СRН | 41,8 | 18,48 | 10,98 | 7,3 | 5,11 | 3,62 | 1,89 | 0,94 | 0,01 |
Ud/U | 2,42 | 2,4 | 2,38 | 2,36 | 2,34 | 2,34 | 2,34 | 2,34 | 2,34 |
Iamax/Id | 9,4 | 6,2 | 4,8 | 3,9 | 3,3 | 2,8 | 2,0 | 1,5 | 1,0 |
Ia/Id | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 | 0,33 |
Ia.д/Id | 1,44 | 1,18 | 1,04 | 0,94 | 0,86 | 0,79 | 0,67 | 0,6 | 0,58 |
IС.д/Id | 2,1 | 1,8 | 1,5 | 1,3 | 1,1 | 0,9 | 0,6 | 0,3 | 0,01 |
cos | 0,99 | 0,99 | 0,98 | 0,98 | 0,97 | 0,97 | 0,98 | 1 | 1 |
| 0,42 | 0,50 | 0,57 | 0,62 | 0,67 | 0,73 | 0,85 | 0,92 | 0,96 |
| 0,41 | 0,49 | 0,55 | 0,61 | 0,66 | 0,71 | 0,83 | 0,92 | 0,96 |