Делитель напряжения на резисторах: онлайн калькулятор расчета
Схема делителя напряжения является простой, но в тоже время фундаментальной электросхемой, которая очень часто используется в электронике. Принцип работы ее прост: на входе подается более высокое входное напряжение и затем оно преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула расчета выходного напряжения основана на законе Ома и приведена ниже.
 Классическая формула делителя напряжения
Классическая формула делителя напряжениягде:
- Uвх. — входное напряжение источника, В;
- Uвых. — выходное напряжение, В;
- R1 — сопротивление 1-го резистора, Ом;
- R2 — сопротивление 2-го резистора, Ом.

В калькулятор ниже введите любые три известных значения Uвх., Uвых. и R1 и нажмите «Рассчитать», чтобы найти значение R2.
Упрощения
Существует несколько обобщений, которые следует учитывать при использовании делителей напряжения. Это упрощения, которые упрощают оценку схемы деления напряжения.
Во-первых, если R2 и R1 равны, то выходное напряжение вдвое меньше входного напряжения. Это верно независимо от значений резисторов.
Итак, если R1 = R2, то получаем следующее уравнение:
 Формула делителя напряжения, если сопротивления равны
Формула делителя напряжения, если сопротивления равныВо-вторых, если R2 на порядок больше чем R1, то выходное напряжение Uвых будет очень близко к Uвх., то есть Uвх. ≈ Uвых. А на R1 будет очень мало напряжения.
 Формула делителя напряжения, если R2 на порядок больше R1
Формула делителя напряжения, если R2 на порядок больше R1Во-третьих, если наоборот R1 на порядок больше чем R2, то Uвых будет очень маленьким по сравнению с Uвх, то есть будет стремиться к нулю. Практически все входное напряжение упадет в таком случае на R1.

Вы можете воспользоваться онлайн калькулятором ниже, чтобы проверить как саму классическую формулу делителя напряжения, представленную на рисунке 1, так и вышеприведенные упрощения этой формулы.
Расчет делителя напряжения на резисторах: онлайн-калькулятор
Делитель напряжения — это простой и удобный способ получить нужное напряжение в определенной точке схемы. Он используется в цепях обратной связи для измерения выходных параметров, когда на выходе десятки вольт, а измерительный вход микросхемы рассчитан на единицы или доли вольт и во множестве других целей. Простейший вариант строится на резисторах их может быть 2 и больше.

Давайте разберемся как рассчитать данный элемент цепи. Можно сделать это вручную или использовать следующий онлайн калькулятор, который выполняет расчет делителя напряжения на резисторах:
Главное, что нельзя забывать, так это то, что ток делителя должен быть на 1 и более порядков выше, чем входной ток нагрузки. Это нужно, чтобы минимизировать просадки напряжения и сохранить стабильность выходных параметров. После этого приступайте к расчетам по току и напряжению.
Если ваш делитель состоит из двух элементов, то ток через него рассчитывают по формуле:
I=Uвх/(R1+R2)=Uвх/Rобщ
Или сопротивление по заданному току:
Rобщ=Uвх/I
Нам известно R общее при заданном I, входное напряжение и сколько нам нужно получить на выходе. Рассчитываем сопротивления:
R2=Uвых*Rобщ/Uвх
Тогда:
R1=Rобщ-R2
Если нужно определить параметры цепочки по известным сопротивлениям и входному напряжению — рассчитывают выходное по формуле:
Uвых=Uвх*R2/R1+R2
Значит, зная напряжение на выходе можно рассчитать его и на входе:
Uвх=(Uвых*R1+R2)/R2
Это основной метод расчета резистивного делителя, бывает еще и емкостной или индуктивный. В этом случае вместо сопротивления активного R в расчетах фигурирует сопротивление реактивное Xc или Xl.
Для регулировки выходного напряжения резисторного делителя вместо нижнего сопротивления устанавливают подстроечный или переменный резистор. Расчеты при этом ничем не отличаются — в них используют максимальное значение на переменном резисторе. Также можно ограничить минимальное выходное напряжение, установив последовательно с переменным постоянное, тогда минимальное рассчитывается без учета переменника. Такую схему удобно использовать, если у вас резисторы с большим допуском, а нужно получить точные выходные параметры.

Вы можете сэкономить время, воспользовавшись онлайн калькулятором, в нем вы можете рассчитать номиналы элементов с учетом нужных выходного и входного напряжения. Использование калькулятора сэкономит ваше время, если нужно посчитать большую схему или вы запутались и не можете разобраться, как посчитать резистивный делитель с нагрузкой.
Учтите, что элементы нужно подбирать не только по номиналу, но и по мощности, потому что при большом токе потребления нагрузки, нужно рассчитывать схему на большие токи. В результатах расчетов онлайн калькулятора будет указано, на сколько ватт нужен резистор.
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.
Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.
В соответствии с законом Ома (1):
 |
Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):
  |
Тогда напряжение на всем участке цепи (4):
 |
Отсюда определим, чему равно значение тока без включения нагрузки (5):
 |
Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):
  |
Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.
Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.
Онлайн подбор сопротивлений для делителя
Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.
Таким образом, напряжения: U=24 B, U2=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:
 |
выразим отсюда R2:
 |
Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):
 |
Ток, который протекает через делитель, находится по формуле (5):
 |
Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):
  |
  |
По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:
| 1. R1=1 кОм, P1=0,324 Вт. | ||
| 2. R2=333,3 Ом, P2=0,108 Вт. |
Полная мощность, которая потеряется:
  |
Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):
 |
| где С – ёмкость конденсатора, Ф; | ||
| f – частота сети, Гц. |
Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):
  |
Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):
 |
| где L – индуктивность, Гн. |

Падение напряжения на индуктивностях (14,15):
|
|
Недостаточно прав для комментирования
Резисторный делитель напряжения: расчёт-онлайн, формулы и схемы
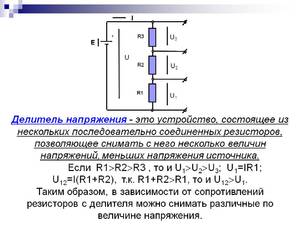 Резисторный делитель напряжения — одна из основополагающих конструкций в электронике, без которой не обходится ни одно устройство. Подбор сопротивлений задаёт нужные режимы работы. Как правило, эта конструкция содержит два резистора. Один ставится между входом и выходом схемы. Второй резистор одним концом подключается к общему проводу, а вторым — к выходу схемы, тем самым его шунтируя. Он также играет роль нагрузки источника, подключённого ко входу.
Резисторный делитель напряжения — одна из основополагающих конструкций в электронике, без которой не обходится ни одно устройство. Подбор сопротивлений задаёт нужные режимы работы. Как правило, эта конструкция содержит два резистора. Один ставится между входом и выходом схемы. Второй резистор одним концом подключается к общему проводу, а вторым — к выходу схемы, тем самым его шунтируя. Он также играет роль нагрузки источника, подключённого ко входу.
Формула делителя напряжения
Расчёт можно осуществить, используя формулы, вытекающие из закона Ома. Можно узнать, каким будет U на выходе устройства, если известно входное, а также сопротивления обоих резисторов. Можно также решить обратную задачу, например, вычислить напряжение, которое получится на выходе при известных сопротивлениях резисторов.
Чтобы выполнить расчет резистивного делителя, необходимо:
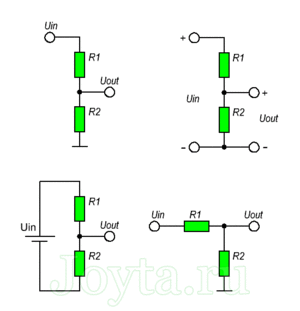
 Обозначить резистор, находящийся ближе ко входу делителя, как R1.
Обозначить резистор, находящийся ближе ко входу делителя, как R1.- Обозначить резистор, находящийся ближе к выходу делителя, как R2.
- Протекающие через резисторы токи обозначаются, как I1 и I2, а входное и выходное напряжения — UВХ и UВЫХ, соответственно.
- Промежуточная формула примет следующий вид: UВЫХ=I2*R2.
- Если предположить, что силы обоих токов равны, то формула для определения протекающего через схему тока станет выглядеть так: I=UВХ/R1+R2.
- Окончательная формула принимает такой вид: UВЫХ=R2*(UВХ/R1+R2).
Из неё становится ясно, что выходное напряжение всегда будет меньше, чем входное. Оно зависит от самих резисторов. Чем больше сопротивление R1 и сила протекающего тока, тем меньше будет UВЫХ. Напротив, чем больше сопротивление R2, включённое между выходом и общим проводом, тем больше будет UВЫХ. Если упомянутое сопротивление стремится к бесконечности, то UВЫХ будет почти равным входному. Чем больше ток, который проходит по резисторам, тем меньше будет UВЫХ. Таким образом при больших токах делитель на резисторах становится малоэффективным, ввиду сильного падения напряжения.
Онлайн-калькуляторы
С их помощью можно рассчитать делитель напряжения на резисторах онлайн. Входными данными в этом случае могут являться: входное напряжение и оба сопротивления. Калькулятор «Делитель напряжения — онлайн» произведёт все необходимые операции по обозначенной формуле, и выведет значения искомых параметров. Расчет делителя напряжения на резисторах онлайн облегчает процесс разработки многих электронных схем, позволяет добиться достижения требуемых режимов и правильной работы устройств.
Разновидности делителей
 Самая распространенная и характерная из них — это потенциометр. Он представляет собой стандартный переменный резистор. Внутри его находится дужка, на которую нанесен токопроводящий слой. По ней скользит контакт, делящий сопротивление на две части. Таким образом, потенциометр имеет три вывода, два из которых подключены к самому резистору, а третий — к перемещаемому движку.
Самая распространенная и характерная из них — это потенциометр. Он представляет собой стандартный переменный резистор. Внутри его находится дужка, на которую нанесен токопроводящий слой. По ней скользит контакт, делящий сопротивление на две части. Таким образом, потенциометр имеет три вывода, два из которых подключены к самому резистору, а третий — к перемещаемому движку.
Источник тока подключается к двум крайним выводам потенциометра, а UВЫХ будет сниматься с вывода движка и общего провода. По такой схеме устроены, например, регуляторы громкости и тембра звука в различной аудиоаппаратуре. При перемещении движка в крайнее нижнее положение UВЫХ станет равным нулю, а в противоположной ситуации будет равно входному. Если же перемещать движок, то напряжение будет плавно изменяться от нуля до входного.
Свойства делителей также используются при конструировании резистивных датчиков. Например, одним из их элементов может являться фоторезистор, изменяющий свое сопротивление в зависимости от освещённости. Есть и другие датчики, преобразующие физические воздействия в изменение сопротивления: терморезисторы, датчики давления, ускорения. Созданные на их основе делители используются совместно с аналого-цифровыми преобразователями для измерения и отслеживания самых различных величин в промышленности и быту: температуры, скорости вращения.
В качестве примера можно привести схему для определения уровня освещенности. Последняя деталь включается между выходом и общим проводом (R2 в формуле). Для расширения пределов изменения напряжения схема дополняется постоянным сопротивлением (R1 в формуле). К её выходу присоединяется микроконтроллер аналого-цифрового преобразователя. Чем сильнее освещённость фоторезистора, тем ниже UВЫХ, так как он включён между выходом конструкции и «массой», шунтируя его.
напряжения на резисторе и после
При разработке печатных плат для электронного оборудования специалистам часто приходится выполнять расчет делителя. С виду простая схема помогает уменьшить выходное напряжение, необходимое для питания отдельных элементов цепи. Такая компоновка является базовой для электроники. В основу изучения принципа действия входят два момента: схематическое исполнение и формула для вычисления параметров работы делителя.
Что такое делитель напряжения
Схематическое исполнение понижающего устройства представляет собой последовательную цепь, состоящую из двух резистивных элементов. Суммарные значения сопротивлений позволяют уменьшить входящее напряжение до необходимых параметров на выходе. Между собой они связаны передаточным коэффициентом, находящимся в интервале от 0 до 1, включая границы (0<=aplha<=1).

Общее представление делителя напряжения
Существует несколько вариантов схематического исполнения приборов, но все они обладают одним и тем же функционалом — понижать вольтаж для потребителей, однако ток на всех полюсах остается одинаковым. Два последовательных участка цепи называют плечами. Нижнее плечо находится между центральной точкой и нулевым потенциалом. Именно здесь необходимо снимать показатели работы схемы. Другое плечо является верхним.

Простая схема на резисторах
В зависимости от расположения резисторов, различают линейные и нелинейные схемы делителей. Первый вариант используют для создания разности потенциалов и вольтажа в нескольких точках рабочих узлов. Понижение входного напряжения определяется по линейному закону.
Дополнительная информация! Понижающие узлы применяют для постоянного и переменного тока. Структурное исполнение обоих отличается друг от друга, поскольку в некоторых случаях требует включение дополнительных фильтров для подавления помех и шумов.
В нелинейных схемах разница определяется по передаточному коэффициенту. Такие устройства активно применяют в потенциометрах. Здесь учитывают присутствие активного и реактивного сопротивления, включая нелинейные и токовые нагрузки.
Принцип работы делителя напряжения
В состав простейшей понижающей схемы всегда входит не меньше одного резистора. Если элементы обладают одинаковыми коэффициентами сопротивляемости электронов, то на выходе вольтаж понизится в два раза. Для каждого узла понижение рассчитывается по закону Ома.
Внимание! Сумма пониженных величин в каждой точке равна общему вольтажу источника питания.

Схема с несколькими резисторами
Резисторы используют в принципиальных схемах с источником питания постоянного тока. В цепях переменного напряжения присутствует еще и реактивное сопротивление, куда входят конденсаторы, индуктивные катушки и другие элементы с электромагнитными полями.
В цепях с синусоидальным током в качестве резистивного элемента выступает конденсатор или катушка. Их называют емкостными. Расчет ведется уже по другой формуле, так как емкость конденсаторов обратно пропорциональна их реактивному сопротивлению. Для вычисления резистивной составляющей необходимо учитывать постоянное число ПИ, частоту синусоидального тока (Гц) и емкость (Фарад). Таким образом получается, что с увеличением емкости падает сопротивление и наоборот.
Кроме конденсаторов, в качестве реактивных компонентов также могут выступать индуктивные катушки, которые могут присутствовать в платах переменного тока. Коэффициент реактивного сопротивления обмоток также прямо пропорционален их номинальным значениям. Для вычислений также необходимо постоянное число ПИ, частота переменного магнитного поля (Гц) и индуктивность (Генри).

Делитель на индукционных катушках
Внимание! В описании выше токовая нагрузка равна бесконечности, поэтому все значения верны только при полученных показателях делителя на сопротивления нагрузки. Они в несколько раз больше внутреннего.
Формула для расчета делителя напряжения
Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:
- U — напряжение, В;
- I — ток, А;
В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно. В формуле использованы показатели:

График зависимости показателей от сопротивления
- R — реактивное сопротивление;
- R — сопротивление, Ом.
- pi — постоянное число Пи, равное 3,14;
- f — частота, Гц;
- L — индуктивность катушки, Генри;
- C — емкость конденсатора, Фарад.
Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.
На резисторе
В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.
После резистора
Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:
- Uвых — вольтаж на выходе, В;
- Uпит — входной вольтаж, В;
- R1 — первый узел, Ом;
- R2 — второй узел, Ом.
Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).
Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.
схема и расчёт [Амперка / Вики]
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов.
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе Vout? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1 и R2 одинаков пока к выходу Vout ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2, расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, Vout будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта Vout.
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
В этом случае Vout уже не может быть расчитано лишь на основе значений Vin, R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта Vout, получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
Пропорция сохраняется, Vout не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, Vout также будет неравномерным.


 Обозначить резистор, находящийся ближе ко входу делителя, как R1.
Обозначить резистор, находящийся ближе ко входу делителя, как R1.