Последовательное соединение резисторов онлайн калькулятор

Уникальнvй софт / Калькулятор соединения резисторов

Калькулятор соединения резисторов v.1.0 — предоставляет возможность быстро вычислить и подобрать номиналы резисторов (до 10-ти резисторов в соединении) для параллельного и последовательного соединения. Вычисляет Rобщ на основе R1-R10 или подбирает нужный R1 для указанного Rобщ (с учетом резисторов R2-R10 при необходимости) для любого типа соединения резисторов (как последовательного так и параллельного). Вычисления делаются автоматически при вводе номиналов резисторов с возможностью отключения автоматического расчета при вводе. Возможен переход в диапазон кОм. Имеется возможность сохранения всех значений в текстовый файл. При необходимости, возможно включить параметр «Поверх всех окон».

Скачать программу Объём 167 кБ Всего загрузок: 1182

При последовательном соединении сопротивления включены одно за другим, так что через каждое сопротивление протекает полный ток.

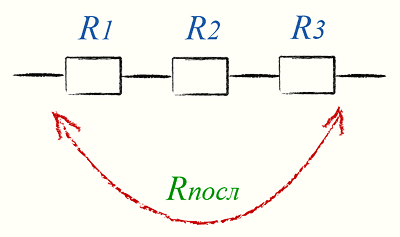
При последовательном соединении сопротивлений полное сопротивление равно сумме отдельных сопротивлений.

Архивы

Онлайн калькулятор для расчета сопротивления в цепи при последовательном соединении резисторов.

Как пользоваться калькулятором

Введите заданное количество резисторов в цепи. Появятся поля с заданным количеством резисторов, укажите значение сопротивления каждого резистора в Ом. Нажмите на красную кнопку «Рассчитать». Результат появятся в поле снизу.

Примечание

Максимальное количество резисторов, которые можно ввести — 1000.

Теория

Резистор — пассивный элемент электроцепей, характеризуется сопротивлением электротоку.

Последовательное соединение — соединение двух или более резисторов в форме цепи. Каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Ом — единица измерения сопротивления. Приставки увеличения: кило — килоом (тысяча Ом), мега — мегаом (миллион Ом).

Формула

Для двух параллельно соединенных резисторов их общее сопротивление равно:

Rобщ. = R1 + R2 + … Rn.

• R1,R2,…Rn значение каждого отдельного резистора,
• Rобщ. — значение последовательных резисторов.

Пример

Известно сопротивление R1 = 2 Ом, R2 = 3 Ом, R3 = 4 Ом.

Требуется найти последовательное сопротивление.

Rобщ. = R1 + R2 + … Rn,

Rобщ. = 2 + 3 + 4 = 9.

Результат : Rобщ. = 9 Ом.

Задание

Рассчитайте с помощью онлайн программы правильно ли решен пример выше.

Калькулятор последовательного соединения резисторов

Для того чтобы определить общее эквивалентное сопротивление, можно воспользоваться точным и удобным калькулятором. Где, внеся данные по количеству резисторов, калькулятор произведет расчет в автоматическом режиме.

Данное соединение является одним из 2-ух видов, в данном случае оба вывода 1-го из резисторов соединяются с выводами 2-го резистора. В иных случаях их принято соединять параллельно или последовательно, чтобы можно было создать схемы сложного типа.

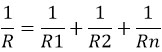
Для того чтобы найти ток, который протекает через определенный резистор, следует использовать формулу: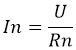
Произведем расчеты согласно примеру
Разрабатывается устройство, в котором есть необходимость использовать резистор, которое имеет сопротивление 8Ом. Исходя из того, что номинальный ряд согласно стандартным значениям таких резисторов не имеет, выходом будет использование 2-ух резисторов соединенных параллельно.

Для такого способа производятся следующие расчеты: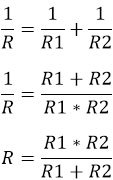

Данная формула показывает, что в случае когда R1 = R2, R будет составлять ровно половину сопротивления 1-го из 2-ух резисторов.
И если R=8Ом, то соответственно R1 и R2 = 2*8=16Ом.

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

Расчёт сопротивления резисторов в параллельном включении. Подбор нужного значения из стандартных номиналов.

Выбираем два имеющихся в наличии номинала E24 и получаем результат их параллельного соединения

Иногда проще вписать значения, чем выбирать селектором.
Результат получаем кликом мыши в любом месте таблицы.

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

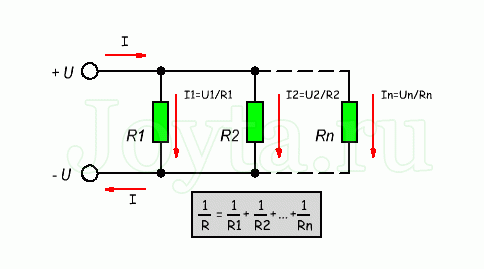
Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

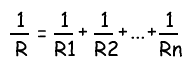
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

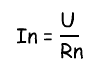
Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

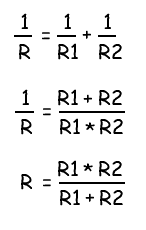
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

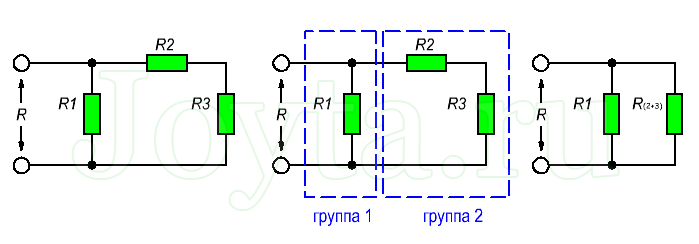
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

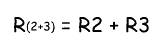
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор расчета импеданса в последовательном соединении элементов цепи

В различных электрических цепях все нагрузки подразделяются на активные, индуктивные и емкостные. В определенных ситуациях все они могут включаться последовательно:

Последовательное соединение элементов цепи

При их последовательном соединении общее сопротивление участка рассчитывается как геометрическое сложение всех векторов сопротивлений нагрузок.

Для математического сложения используется теорема Пифагора, применив которую получим формулу расчета импеданса последовательной цепи:

Где, Z – полное сопротивление (комплексное),  R – активное сопротивление, как правило, выражаемое резистивной нагрузкой, X – реактивное сопротивление, определяемое геометрической сумой сопротивлений индуктивной и емкостной составляющих. Геометрически обе эти величины лежат в одной плоскости, но имеют противоположное направление, поэтому полное реактивное сопротивление рассчитывается по формуле:

X = X_L — X_C

Для определения индуктивного и емкостного сопротивления, при известных параметрах катушки и конденсатора расчет выполняется по формулам:

X_L = w * L = 2 * π * f  * L,

 

 

 

Чтобы определить углы между соответствующими составляющими импеданса в последовательной цепи используются арктангенс для соотношений активного и реактивного сопротивления. А расчет выполняется по формулам:

Как видите, осуществление подобного расчета достаточно сложная и трудоемкая процедура. Поэтому для упрощения работы для определения импеданса при последовательном соединении гораздо легче воспользоваться онлайн калькулятором. В нем вам потребуется указать частоту, емкость, индуктивность и активное сопротивление, а программа произведет все вычисления самостоятельно.

Расчет импеданса в параллельном соединении элементов цепи

Любая электрическая цепь включает в себя ряд элементов, среди которых встречаются активные и реактивные составляющие. При параллельном соединении активного, емкостного и индуктивного элемента схема выглядит таким образом:

Рис. 1. Параллельное соединение элементов электрической цепи

В зависимости от конкретной ситуации тот или иной элемент может исключаться из цепи, меняя тем самым характер нагрузки. Для геометрического определения суммарного значения всех сопротивлений производится сложение векторов. В зависимости от типа реактивной нагрузки результирующий вектор импеданса будет смещаться в положительный или отрицательный квадрант.

Рис. 2. Векторное сложение сопротивления

Для вычисления полного сопротивления Z составляется уравнение согласно теоремы пифагора. Только сложению подлежит не сопротивление, а проводимость цепи. Из-за чего уравнение для определения сопротивления можно будет выразить по следующей формуле:

Где Z – комплексное сопротивление участка,  R – активное сопротивление участка, X – реактивное сопротивление участка.

При этом реактивное сопротивление выражается как геометрическая сумма проводимости катушки и конденсатора.

А отдельно расчет X_L и X_C при известных параметрах сети, емкости и индуктивности самих элементов выполняется по таким формулам:

X_L = w * L = 2 * π * f  * L,

 

 

 

Для определения углов δ и φ необходимо применить тригонометрические функции к отношению соответствующих проводимостей или сопротивлений.

В связи с большим количеством расчетов, применяемых формул и необходимостью использования тригонометрических функций определение импеданса в параллельной цепи является достаточно сложной задачей, особенно, если делать это вручную. Но, при использовании онлайн калькулятора для расчета комплексного сопротивления достаточно ввести частоту, емкость конденсатора, индуктивность катушки и омическое сопротивление резистора. А все расчеты система произведет самостоятельно.

Онлайн калькулятор расчета последовательного соединения конденсаторов

Физически, каждый из конденсаторов является разрывом в цепи, который накапливает и передает заряд за счет подачи на него переменного напряжения. Последовательное соединение конденсаторов подразумевает под собой подключение конца одного емкостного элемента к началу второго. Поэтому при последовательном включении через все конденсаторы протекает один ток, который зависит от их емкости и частоты напряжения в сети. В электротехнике такой тип подключения элементов нашел широкое применение в радиоэлектронике современных компьютеров, радиостанций и прочих устройств.

Рис. 1. Последовательное соединение конденсаторов

 

Как видите на рисунке 1, в нормальном режиме работы системы через все конденсаторы происходит передача электроэнергии, но в случае перегорания какого-либо емкостного элемента или сразу нескольких прекращается электроснабжение всех деталей. Для замены такого элемента в цепи необходимо установить другой конденсатор или заменить его на несколько. При отсутствии элемента нужной емкости вам пригодиться такой способ для перерасчета.

Формула для подсчета суммарной емкости последовательно соединенных конденсаторов выглядит таким образом:

Где, С₀ — общая емкость последовательно соединенных конденсаторов

С₁ — емкость первого конденсатора;

С₂ — емкость второго конденсатора;

С_n — емкость n-ого конденсатора в цепи.

Как видите, процесс расчета потребует от вас длительных и кропотливых операций, поэтому гораздо проще воспользоваться онлайн калькулятором для вычисления суммарной емкости последовательно соединенных конденсаторов.

Понравилась статья? Поделиться с друзьями:

Онлайн калькулятор расчета параллельного соединения конденсаторов

В устройствах радиоэлектроники конденсаторы представляют собой один из важнейших элементов, способный накапливать и отдавать электрический заряд. В сравнении с другими элементами, конденсатор обладает такими параметрами как емкость и сопротивление. Сопротивление конденсатора обусловлено изолирующим промежутком, который может выйти со строя из-за скачков напряжения или других аварийных процессов в сети. При необходимости заменить какой-либо конденсатор, многие радиолюбители сталкиваются с трудностью достать модель нужной емкости.

В таком случае на помощь придет правило сложения, позволяющее заменить одно устройство несколькими меньшей емкости, чтобы в суме их хватило для компенсации вышедшего со строя конденсатора. В этом месте многие не могут определить, каким способом вычисляется суммарная мощность параллельно соединенных конденсаторов. Следует отметить, что физически для схемы конденсатор представляет собой разрыв.

Рис. 1. Параллельное соединение конденсаторов

Посмотрите на рисунок 1, это принципиальная схема параллельного подключения конденсаторов. Как видите, в этом случае одноименные выводы емкостного элемента подводятся к соответствующей точке электрической цепи. Поэтому и емкость между плоскостями двух  и более конденсаторов, соединенных между собой параллельно складывается в одно целое. Исходя из этого, суммарная емкость для параллельно включенных конденсаторов будет вычисляться по формуле:

С₀ = С₁ + С₂ + … + С_n

Где,

• С₀ — общая емкость параллельно соединенных конденсаторов
• С₁ — емкость первого конденсатора;
• С₂ — емкость второго конденсатора.

В данном примере рассматривается ситуация, когда параллельно соединяются только два емкостных элемента, поэтому их результирующая емкость будет равна арифметической сумме емкостей обоих конденсаторов. На практике можно применять и большее число, если вам необходимо получить определенную емкость.

Чтобы рассчитать результирующую емкость при параллельном соединении 2 и более конденсаторов вы можете воспользоваться нашим онлайн калькулятором ниже.