Параллельное соединение цепи. Основные электрические величины цепи. Термины, применяемые к электрическим цепям
Во многих электрических схемах мы можем обнаружить последовательное и . Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,
откуда следует
R экв = R 1 + R 2 + R 3 .
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис.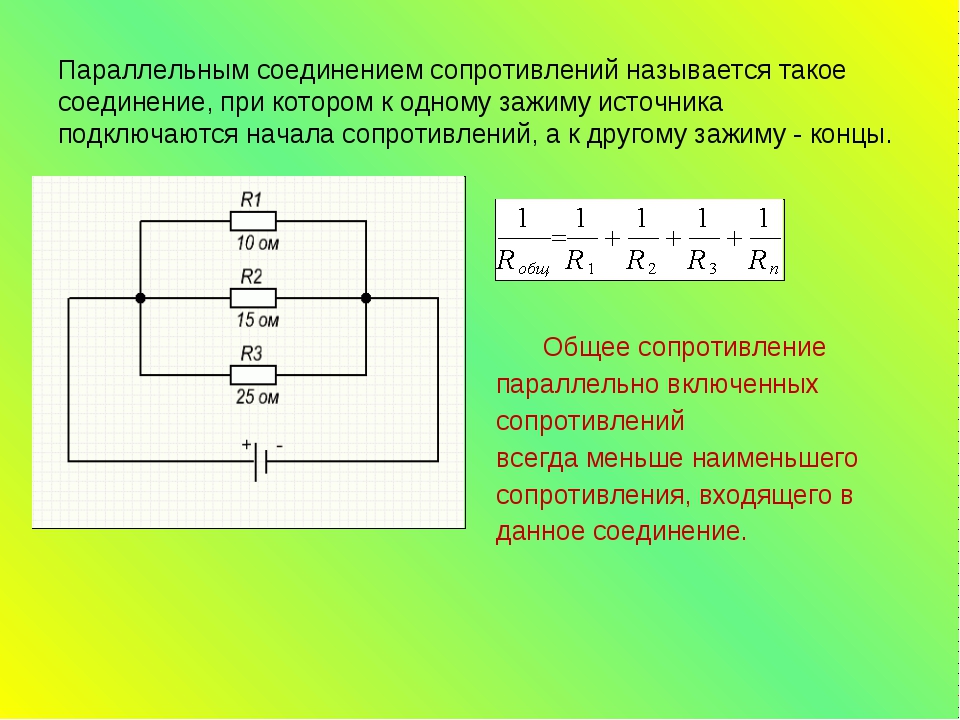 1.6).
1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I 1 + I 2 + I 3 , т.е.
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
g экв = g 1 + g 2 + g 3 .
По мере роста числа параллельно включенных потребителей проводимость цепи g экв возрастает, и наоборот, общее сопротивление R экв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .
Отсюда следует, что
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
Рис. 1.10 | Рис. 1.11 |
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным
преимуществом синусоидальных токов
является то, что они позволяют наиболее
экономично осуществлять производство,
передачу, распределение и использование
электрической энергии. Целесообразность
их использования обусловлена тем, что
коэффициент полезного действия
генераторов, электрических двигателей,
трансформаторов и линий электропередач
в этом случае оказывается наивысшим.
Целесообразность
их использования обусловлена тем, что
коэффициент полезного действия
генераторов, электрических двигателей,
трансформаторов и линий электропередач
в этом случае оказывается наивысшим.
Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б ).
Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е . Нагрузку подключают к генератору с помощью щеток 1 , прижимающихся к двум контактным кольцам 2 , которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В , размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v н :
e = Blv н (2.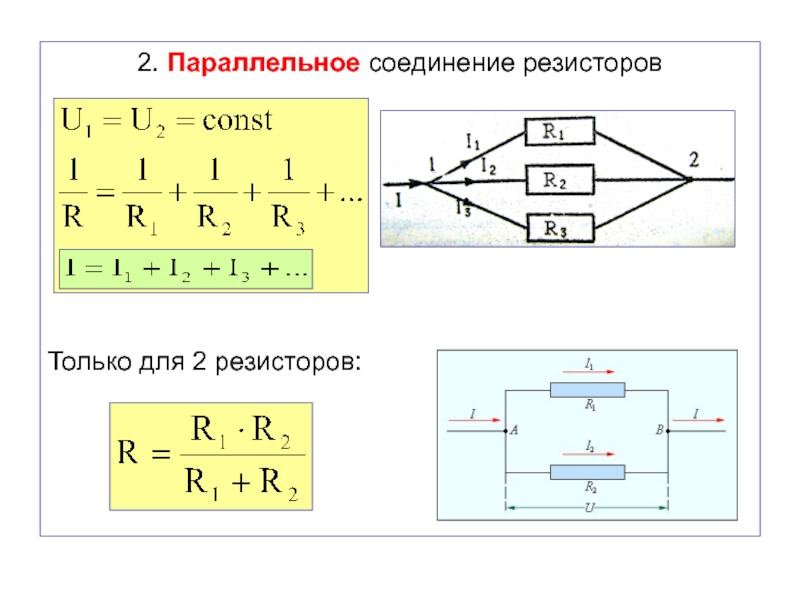 1)
1)
где В и l — постоянные величины, a v н — переменная, зависящая от угла α. Выразив скорость v н через линейную скорость катушки v , получим
e = Blv·sinα (2.2)
В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α .
Если угол α = π/2 , то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E m = Blv . Поэтому выражение (2.2) можно записать в виде
e = E m sinα
Так как α есть угол поворота за время t , то, выразив его через угловую скорость ω , можно записать α = ωt , a формулу (2.3) переписать в виде
e = E m sinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д.
с. в данный момент времени.
д.
с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е , напряжений и и токов i справедливы законы постоянного тока.
Синусоидальные
величины можно графически изображать
синусоидами и вращающимися векторами.
При изображении их синусоидами на
ординате в определенном масштабе
откладывают мгновенные значения величин,
на абсциссе — время. Если синусоидальную
величину изображают вращающимися
векторами, то длина вектора в масштабе
отражает амплитуду синусоиды, угол,
образованный с положительным направлением
оси абсцисс, в начальный момент времени
равен начальной фазе, а скорость вращения
вектора равна угловой частоте. Мгновенные
значения синусоидальных величин есть
проекции вращающегося вектора на ось
ординат. Необходимо отметить, что за
положительное направление вращения
радиус-вектора принято считать направление
вращения против часовой стрелки.
Если число пар полюсов магнитов p ≠ 1 , то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn
Из рис. 2.2 видно, что ωТ = 2π , откуда
ω = 2π / T = 2πf (2.5)
Величину ω , пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е» можно описать выражениями
e = E m sinωt; e» = E» m sin(ωt + ψ e» ) .
Здесь ωt и ωt + ψ e» — фазы, характеризующие значения э. д.
с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение
э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения
синусоидальной величины при переходе
ее от отрицательных значений к
положительным до начала координат (t =
0). При этом положительную начальную
фазу ψ (рис. 2.2) откладывают влево от начала
координат (в сторону отрицательных
значений ωt ),
а отрицательную фазу — вправо.
д.
с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение
э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения
синусоидальной величины при переходе
ее от отрицательных значений к
положительным до начала координат (t =
0). При этом положительную начальную
фазу ψ (рис. 2.2) откладывают влево от начала
координат (в сторону отрицательных
значений ωt ),
а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность
углов φ ,
равная разности начальных фаз, называют
углом сдвига
фаз. Сдвиг фаз
между одноименными синусоидальными
величинами, например между двумя э. д.
с. или двумя токами, обозначают α . Угол сдвига фаз между синусоидами тока
и напряжения или их максимальными
векторами обозначают буквой φ (рис. 2.3).
Угол сдвига фаз между синусоидами тока
и напряжения или их максимальными
векторами обозначают буквой φ (рис. 2.3).
Когда для синусоидальных величин разность фаз равна ±π , то они противоположны по фазе, если же разность фаз равна ±π/2 , то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = U m sin(ω t + ψ u ) ; i = I m sin(ω t + ψ i ) , (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ u — ψ i .
Уравнения (2.6) можно записать иначе:
u = U m sin(ωt + ψ i + φ) ; i = I m sin(ωt + ψ u — φ) ,
поскольку ψ u = ψ i + φ и ψ i = ψ u — φ .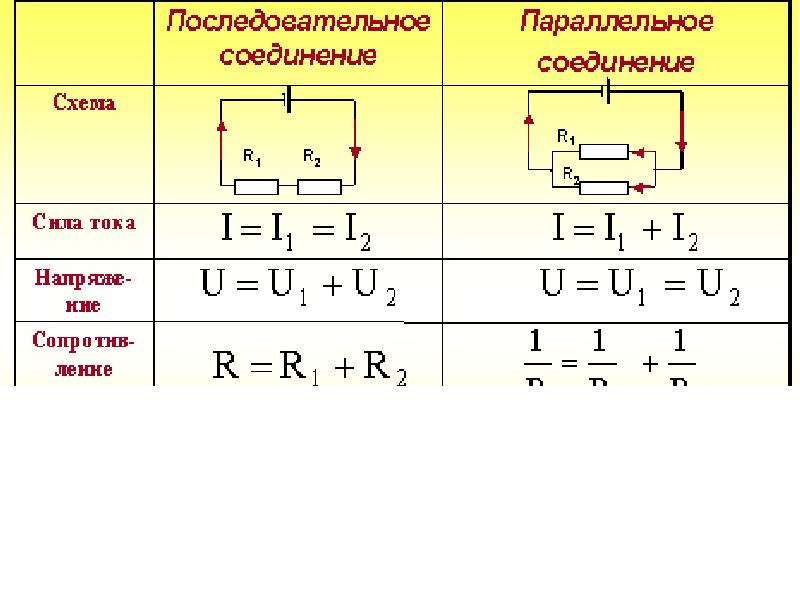
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = I m ·sin(ω·t + ψ i ), u = U m ·sin(ω·t + ψ u ), e = E m ·sin(ω·t + ψ e ),
где I , u , e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
I m , U m , E m – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψ i , ψ u , ψ e
– начальные фазы тока, напряжения, ЭДС
отсчитываются от точки перехода
синусоидальной функции через нуль к
положительному значению до начала
отсчета времени (t = 0). Начальная фаза может иметь как
положительное так и отрицательное
значение.
Начальная фаза может иметь как
положительное так и отрицательное
значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ i φ . Сдвиг фаз между напряжением и током
φ = ψ u – ψ i = ψ u – (- ψ i) = ψ u + ψ i .
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На
практике приходится иметь дело не с
мгновенными значениями синусоидальных
величин, а с действующими. Все расчёты
проводят для действующих значений, в
паспортных данных различных
электротехнических устройств указаны
действующие значения (тока, напряжения),
большинство электроизмерительных
приборов показывают действующие
значения. Действующий ток является
эквивалентом постоянного тока, который
за одно и то же время выделяет в резисторе
такое же количество тепла, как и переменный
ток.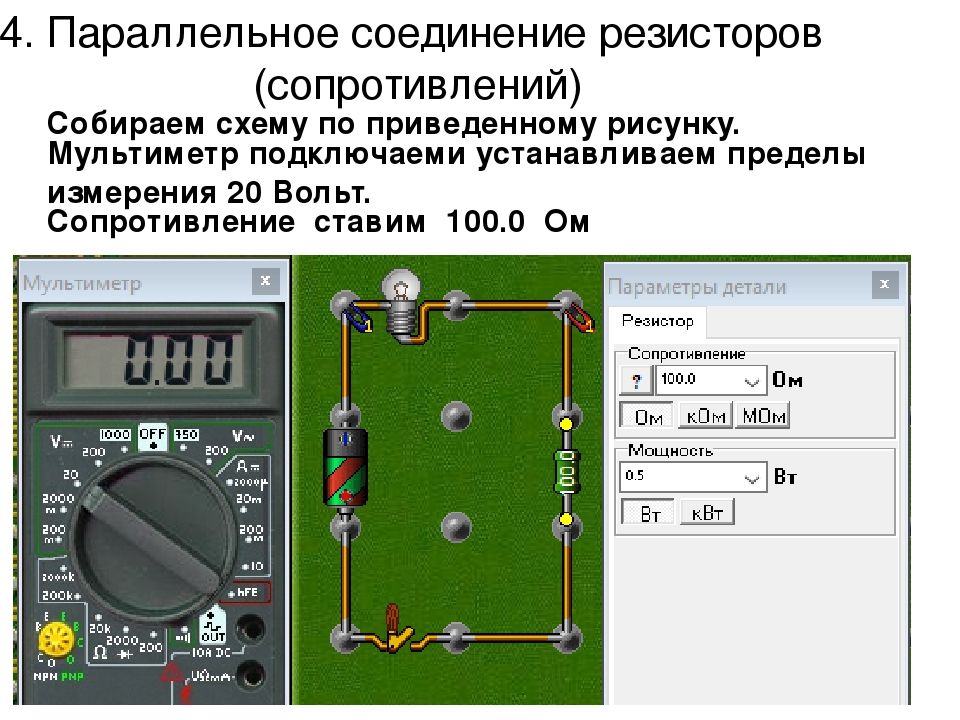 Действующее значение связано с
амплитудным простым соотношением
Действующее значение связано с
амплитудным простым соотношением
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf . Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
Рис. 2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
Рис. 2.5
Ток
и напряжение изобразим в виде векторов
на комплексной плоскости, рис.2.5 Ось
абсцисс называют осью действительных
чисел и обозначают +1 ,
ось ординат называют осью мнимых чисел
и обозначают +j . (В некоторых учебниках ось действительных
чисел обозначают Re ,
а ось мнимых – Im ).
Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует
комплексное число, которое может быть
представлено в трех формах:
(В некоторых учебниках ось действительных
чисел обозначают Re ,
а ось мнимых – Im ).
Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует
комплексное число, которое может быть
представлено в трех формах:
а). Алгебраической
U = U ’+ jU «
I = I ’ – jI «,
где U «, U «, I «, I » – проекции векторов на оси действительных и мнимых чисел.
б). Показательной
где U , I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.
в). Тригонометрической
U = U ·(cosψ u + j sinψ u)
I = I ·(cosψ i
– j sinψ i).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
е j ·ψ = cosψ + j sinψ .
Неразветвлённые электрические цепи
Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.
Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.
Рисунок 1 — последовательное соединение проводников
Падение напряжения на сопротивлениях можно определить исходя из закона Ома.
Формула 1 — Падение напряжения на сопротивлении
Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.
Формула 2 — соотношение между сопротивлением и напряжением
Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.
Формула 3 — вычисление суммарного сопротивления при параллельном включении
Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.
Рисунок 2 — Параллельное соединение проводников
Формула 4 — соотношение между токами в параллельных ветвях
Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.
Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.
Формула 5 — Распределение токов в параллельных ветвях
Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.
Формула 6 — Сопротивление параллельно включённых проводников
Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.
В электротехнике и электронике очень широко используются резисторы. Применяются они в основном для регулирования в схемах тока и напряжения. Основные параметры: электрическое сопротивление (R) измеряется в Омах, мощность (Вт) , стабильность и точность их параметров в процессе эксплуатации. Можно вспомнить ещё множество его параметров, — ведь это обычное промышленное изделие.
Последовательное соединение
Последовательное соединение — это такое соединение, при котором каждый последующий резистор подключается к предыдущему, образуя неразрывную цепь без разветвлений. Ток I=I1=I2 в такой цепи будет одинаковым в каждой её точке. Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
Ток I=I1=I2 в такой цепи будет одинаковым в каждой её точке. Напротив, напряжение U1, U2 в различных её точках будет разным, причём работа по переносу заряда через всю цепь, складывается из работ по переносу заряда в каждом из резисторов, U=U1+U2. Напряжение U по закону Ома равно току, умноженному на сопротивление, и предыдущее выражение можно записать так:
где R — общее сопротивление цепи. То есть по простому идет падение напряжения в точках соединения резисторов и чем больше подключенных элементов, тем больше происходит падение напряжения
Отсюда следует, что
, общее значение такого соединения определяется суммированием сопротивлений последовательно. Наши рассуждения справедливы для любого количества последовательно соединяемых участков цепи.
Параллельное соединение
Объединим начала нескольких резисторов (точка А). В другой точке (В) мы соединим все их концы. В результате получим участок цепи, который называется параллельным соединением и состоит из некоторого количества параллельных друг другу ветвей (в нашем случае – резисторов). При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
При этом электрический ток между точками А и B распределится по каждой из этих ветвей.
Напряжения на всех резисторах будут одинаковы: U=U1=U2=U3, их концы — это точки А и В.
Заряды, прошедшие за единицу времени через каждый резистор, в сумме образуют заряд, прошедший через весь блок. Поэтому суммарный ток через изображенную на рисунке цепь I=I1+I2+I3.
Теперь, использовав закон Ома, последнее равенство преобразуется к такому виду:
U/R=U/R1+U/R2+U/R3.
Отсюда следует, что для эквивалентного сопротивления R справедливо:
1/R=1/R1+1/R2+1/R3
или после преобразования формулы мы можем получить другую запись, такого вида:
.
Чем большее количество резисторов (или других звеньев электрической цепи, обладающих некоторым сопротивлением) соединить по параллельной схеме, тем больше путей для протекания тока образуется, и тем меньше общее сопротивление цепи.
Следует отметить, что обратная сопротивлению величина называется проводимостью. Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Можно сказать, что при параллельном соединении участков цепи складываются проводимости этих участков, а при последовательном соединении – их сопротивления.
Примеры использования
Понятно, что при последовательном соединении, разрыв цепи в одном месте приводит к тому, что ток перестает идти по всей цепи. Например, ёлочная гирлянда перестаёт светить, если перегорит всего одна лампочка, это плохо.
Но последовательное соединение лампочек в гирлянде даёт возможность использовать большое количество маленьких лампочек, каждая из которых рассчитана на напряжение сети (220 В), делённое на количество лампочек.
Последовательное соединение резисторов на примере 3-х лампочек и ЭДС
Зато при последовательном подключении предохранительного устройства его срабатывание (разрыв плавкой вставки) позволяет обесточить всю электрическую цепь, расположенную после него и обеспечить нужный уровень безопасности, и это хорошо. Выключатель в сеть питания электроприбора включается также последовательно.
Параллельное соединение также широко используется. Например, люстра – все лампочки соединены параллельно и находятся под одним и тем же напряжением. Если одна лампа перегорит, — не страшно, остальные не погаснут, они остаются под тем же самым напряжением.
Параллельное соединение резисторов на примере 3-х лампочек и генератора
При необходимости увеличения способности схемы рассеивать тепловую мощность, выделяющуюся при протекании тока, широко используются и последовательное, и параллельное объединение резисторов. И для последовательного, и параллельного способов соединения некоторого количества резисторов одного номинала общая мощность равна произведению количества резисторов на мощность одного резистора.
Смешанное соединение резисторовТакже часто используется смешанное соединение. Если,например необходимо получить сопротивление определенного номинала, но его нет в наличии можно воспользоваться одним из выше описанных способов или воспользоваться смешанным соединением.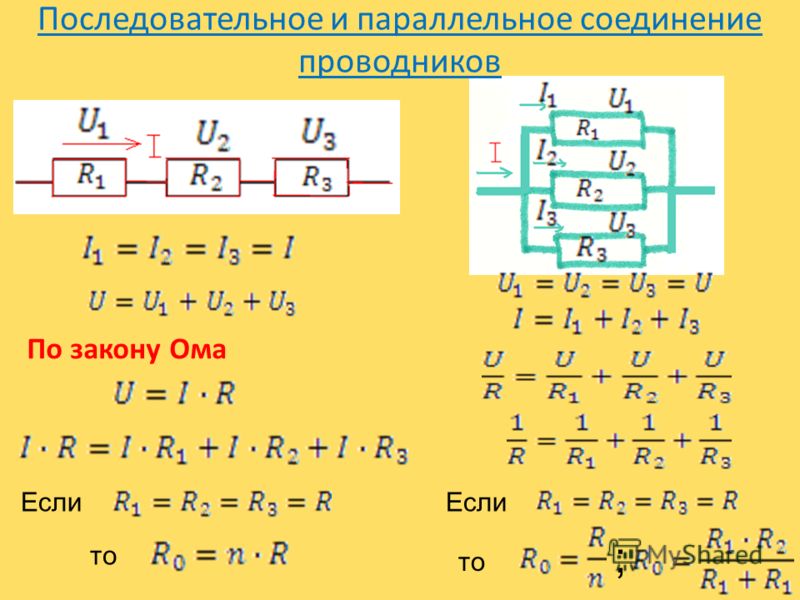
Отсюда, можно вывести формулу которая и даст нам необходимое значение:
Rобщ.=(R1*R2/R1+R2)+R3
В нашу эпоху развития электроники и различных технических устройств в основе всех сложностей лежать простые законы, которые поверхностно рассматриваются на данном сайте и думаю, что вам они помогут успешно применять в своей жизни. Если например взять ёлочную гирлянду, то соединения лампочек идет друг за другом, т.е. грубо говоря это отдельно-взятое сопротивление.
Не так давно гирлянды стали соединятся смешанным способом. Вообще, в совокупности все эти примеры с резисторами взяты условно, т.е. любым элементом сопротивления может быть ток проходящий через элемент с падением напряжения и выделением тепла.
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое
сопротивле́ние —
физическая величина, характеризующая
свойства проводника препятствовать
прохождению электрического
тока и
равная отношениюнапряжения на
концах проводника к силе
тока,
протекающего по нему . Сопротивление для цепей переменного
тока и для переменных электромагнитных
полей описывается понятиями импеданса и волнового
сопротивления. Сопротивлением (резистором)
также называют радиодеталь, предназначенную
для введения в электрические цепи
активного сопротивления.
Сопротивление для цепей переменного
тока и для переменных электромагнитных
полей описывается понятиями импеданса и волнового
сопротивления. Сопротивлением (резистором)
также называют радиодеталь, предназначенную
для введения в электрические цепи
активного сопротивления.
Сопротивление (часто обозначается буквой R или r ) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
R — сопротивление;
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
По закону Ома, напряжения U 1 и U 2 на проводниках равны
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив
для любого числа последовательно
соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U 1 и U 2 на обоих проводниках одинаковы:
Этот результат следует из того, что в точках разветвления токов (узлы A и B ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд I Δt , а утекает от узла за то же время заряд I 1 Δt + I 2 Δt . Следовательно,I = I 1 + I 2 .
Записывая на основании закона Ома
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного
и параллельного соединения проводников
позволяют во многих случаях рассчитывать
сопротивление сложной цепи, состоящей
из многих резисторов. На рис. 1.9.3
приведен пример такой сложной цепи и
указана последовательность вычислений.
1.9.3
приведен пример такой сложной цепи и
указана последовательность вычислений.
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Калькулятор цветовой маркировки резисторов • электротехнические и радиотехнические калькуляторы • онлайн-конвертеры единиц измерения
Ряд Е192
Является наибольшее число номиналов, ряд включает в себя 192 единицы возможных вариантов и предоставляет самый широкий спектр для выбора. Отличается такими данными:
погрешность сопротивления не может превышать 0,5%, 0,25 и даже 0,1%, что выводит их в категорию сверхточного оборудования, часто на их основе разрабатывают smd резисторы;
- с точки зрения цветового обозначения ряда, то на корпусе прибора изображается зеленая, синяя или фиолетовая полоска;
- применяется в сверхточных измерительных комплексах и электронно-вычислительных машинах.

Существенный недостаток – самая высокая стоимость, в сравнении с другими. Для удобства понимания разницы между номинальными рядами трех последних порядков ниже приведена таблица с значениями сопротивлений резисторов.
Таблица: номиналы рядов Е48, Е96, Е192
Таблица: номиналы рядов Е48, Е96, Е192
Ряд Е6
Здесь для обозначения номиналов содержится шесть возможных величин: 1; 1,5; 2,2; 3,3; 4,7; 6,8. При указании номинальных емкостей, сопротивлений и других характеристик радиодеталей, Е6 обладает такими отличиями:
- величина допуска на погрешность составляет не более 20%, что дает немалое отклонение, которое обязательно следует учитывать при работе точных приборов;
- при использовании цветовых маркировок для керамических или углеродистых резисторов, детали будут иметь черную полосу, характеризующую их возможную погрешность;
Определение допустимого отклонения по цветовой маркировке
наибольшее распространение они получили в силовом оборудовании, где основная роль резистора заключается в гашении величины токовой нагрузки, а существующая погрешность не окажет существенного влияния.
Ряд Е12
В сравнении с предыдущим, будет иметь уже не шесть, а двенадцать вариантов номиналов для электронных компонентов от 1 до 8,2. Значение номинальных данных имеет пропорциональное увеличение.
По своим характеристикам ряды Е12 отличаются следующими данными:
- допустимая погрешность катушек индуктивности или резисторов составляет не больше 10%;
- если у резистора имеется цветная маркировка, то полоска, указывающая на возможное отклонение от заявленного сопротивления должна иметь серый или серебристый цвет;
- их сфера применения охватывает сферу подстроечных и переменных резисторов, также используется для некоторых бытовых приборов.
Ряд Е48
Количество вариантов сопротивления электрическому току еще в два раза превосходит Е24, начиная с него, номиналы разделяются не только десятыми, но уже и сотыми долями. Отличительной особенностью этого и последующих рядов является их высокая точность, а именно, Е48 может отклоняться от заявленных данных всего на 2%.
Для обозначения ряда Е48 из цветных полос наносится красного цвета, в работе бытовых приборов подобное отклонение совершенно незаметно, так как обычные колебания напряжения в электрической цепи оказывают куда более существенное влияние. Поэтому их использование в моделировании имеет узконаправленную специфику и принадлежит к точным элементам.
Катушки индуктивности
Последовательное соединение катушек индуктивности
При соединении катушек индуктивности последовательно суммарная индуктивность равна сумме индуктивности всех катушек, но при условии что, при последовательном соединении катушек индуктивности магнитные поля их не влияют друг на друга.
Lобщ=L1+L2+L3+…+Ln
Параллельное соединение катушек индуктивности
При параллельном соединении катушек индуктивности общая индуктивность (при условии что магнитные поля катушек индуктивности не влияют друг на друга) определяется по формуле:
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Номинальные ряды с большим числом элементов
Ряд E48 соответствует относительной точности ±2 %, E96 — ±1 %, E192 — ±0,5 %. Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 10 1/48 ≈ 1,04914, 10 1/96 ≈ 1,024275, 10 1/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.
Хотя элементы этих рядов образуют строгую геометрическую прогрессию со знаменателями 10 1/48 ≈ 1,04914, 10 1/96 ≈ 1,024275, 10 1/192 ≈ 1,01206483 и легко могут быть вычислены на калькуляторе, тем не менее для удобства приведём и эти ряды.
Номинальные ряды E48, E96, E192
E48
E96
E192
E48
E96
E192
E48
E96
E192
E48
E96
E192
E48
E96
E192
E48
E96
E192
1,00
1,00
1,00
1,47
1,47
1,47
2,15
2,15
2,15
3,16
3,16
3,16
4,64
4,64
4,64
6,81
6,81
6,81
1,01
1,49
2,18
3,20
4,70
6,90
1,02
1,02
1,50
1,50
2,21
2,21
3,24
3,24
4,75
4,75
6,98
6,98
1,04
1,52
2,23
3,28
4,81
7,06
1,05
1,05
1,05
1,54
1,54
1,54
2,26
2,26
2,26
3,32
3,32
3,32
4,87
4,87
4,87
7,15
7,15
7,15
1,06
1,56
2,29
3,36
4,93
7,23
1,07
1,07
1,58
1,58
2,32
2,32
3,40
3,40
4,99
4,99
7,32
7,32
1,09
1,60
2,34
3,44
5,05
7,41
1,10
1,10
1,10
1,62
1,62
1,62
2,37
2,37
2,37
3,48
3,48
3,48
5,11
5,11
5,11
7,50
7,50
7,50
1,11
1,64
2,40
3,52
5,17
7,59
1,13
1,13
1,65
1,65
2,43
2,43
3,57
3,57
5,23
5,23
7,68
7,68
1,14
1,67
2,46
3,61
5,30
7,77
1,15
1,15
1,15
1,69
1,69
1,69
2,49
2,49
2,49
3,65
3,65
3,65
5,36
5,36
5,36
7,87
7,87
7,87
1,17
1,72
2,52
3,70
5,42
7,96
1,18
1,18
1,74
1,74
2,55
2,55
3,74
3,74
5,49
5,49
8,06
8,06
1,20
1,76
2,58
3,79
5,56
8,16
1,21
1,21
1,21
1,78
1,78
1,78
2,61
2,61
2,61
3,83
3,83
3,83
5,62
5,62
5,62
8,25
8,25
8,25
1,23
1,80
2,64
3,88
5,69
8,35
1,24
1,24
1,82
1,82
2,67
2,67
3,92
3,92
5,76
5,76
8,45
8,45
1,26
1,84
2,71
3,97
5,83
8,56
1,27
1,27
1,27
1,87
1,87
1,87
2,74
2,74
2,74
4,02
4,02
4,02
5,90
5,90
5,90
8,66
8,66
8,66
1,29
1,89
2,77
4,07
5,97
8,76
1,30
1,30
1,91
1,91
2,80
2,80
4,12
4,12
6,04
6,04
8,87
8,87
1,32
1,93
2,84
4,17
6,12
8,98
1,33
1,33
1,33
1,96
1,96
1,96
2,87
2,87
2,87
4,22
4,22
4,22
6,19
6,19
6,19
9,09
9,09
9,09
1,35
1,98
2,91
4,27
6,26
9,19
1,37
1,37
2,00
2,00
2,94
2,94
4,32
4,32
6,34
6,34
9,31
9,31
1,38
2,03
2,98
4,37
6,42
9,42
1,40
1,40
1,40
2,05
2,05
2,05
3,01
3,01
3,01
4,42
4,42
4,42
6,49
6,49
6,49
9,53
9,53
9,53
1,42
2,08
3,05
4,48
6,57
9,65
1,43
1,43
2,10
2,10
3,09
3,09
4,53
4,53
6,65
6,65
9,76
9,76
1,45
2,13
3,12
4,59
6,73
9,88
В 1952 году IEC (IEC — международная электротехническая комиссия) утвердила стандартные значения для резисторов, называемые номинальный ряд резисторов.
История создание номинального ряда резисторов началась в первые годы прошлого века, в то время когда большинство были углеродно-графитовыми с относительно большими производственными допусками.
Идея создания номинального ряда довольно простая — установить стандартные значения для резисторов на основе допусков, с которыми они могут быть изготовлены.
Цветовая маркировка резисторов.
Большинство резисторов имеют цветовую маркировку
, такую как на этом рисунке. Она представляет из себя 4 или 5 полос (чаще всего, хотя их может быть, например, и 6) определенных цветов, и каждая из этих полос несет определенный смысл. Первые две полоски абсолютно всегда обозначают первые две цифры номинального сопротивления резистора. Если полосок всего 3 или 4, то третья полоса будет означать множитель, на который необходимо умножить число, полученное из первых двух полос, для определения величины сопротивления. Если всего на резисторе 4 полосы, то 4 будет указывать на точность резистора. Если полос всего пять, то ситуация несколько меняется — первые три полосы означают три цифры сопротивления резистора, четвертая — множитель, пятая — точность. Соответствие цифр цветам приведено в таблице:
Если полос всего пять, то ситуация несколько меняется — первые три полосы означают три цифры сопротивления резистора, четвертая — множитель, пятая — точность. Соответствие цифр цветам приведено в таблице:
Тут есть еще один немаловажный момент — а какую именно полосу считать первой? Чаще всего первой считается та полоса, которая находится ближе к краю резистора. Кроме того, можно заметить, что золотая и серебряная полосы не могут быть первыми, поскольку не несут информации о величине сопротивления. Поэтому если на резисторе есть полосы этого цвета и они расположены с краю, то можно точно утверждать, что первая полоса находится с противоположной стороны. Давайте рассмотрим практический пример:
Поскольку у нас здесь 5 полос, то первые три указывают на сопротивление резистора. Посмотрев нужные значения в таблице, мы получаем величину 510. Четвертая полоса — множитель — в данном случае он равен . И, наконец, пятая полоса — погрешность — 10 %. В итоге мы получаем резистор 510 КОм, 10 %.
В принципе, если нет желания разбираться с цветами и значениями, то можно обратиться к какому-нибудь автоматизированному сервису, определяющему сопротивление по цветовой маркировке, которых сейчас полно в интернете. Там нужно будет только выбрать цвета, которые нанесены на резистор и сервис сам выдаст величину сопротивления и точность.
Итак, с цветовой маркировкой резисторов
мы разобрались, переходим к следующему вопросу
Помимо цветовой маркировки используется так называемая кодовая — для обозначения номинала резистора в данном случае используются буквы и цифры (четыре или пять знаков). Первые знаки (все, кроме последнего) используются для обозначения номинала резистора и включают в себя две или три цифры и букву. Буква определяет положение запятой десятичного знака, а также множитель. Последний же символ определяет допустимое отклонение сопротивления резистора. Возможны следующие значения:
Для букв, обозначающих множитель возможны такие варианты:
Давайте для наглядности рассмотрим несколько примеров:
С этим типом маркировки мы разобрались, давайте теперь изучим всевозможные способы маркировки SMD резисторов.
Номиналы резисторов — онлайн калькулятор
Для удобства приводим калькулятор для быстрого подбора сопротивления из стандартного номинального ряда резисторов.
Примечание:
в окошко «Введите необходимое сопротивление» вписывайте значение без префиксов (кОм, МОм). Например, для поиска ближайшего значения для сопротивления 38 Ом – вводим 38. То же самое справедливо и для 38 кОм – вводим 38 (не забывая, что результат относится к кОм)
Под этим термином что только не подразумевается. Если просмотреть статьи в интернете, посвященные данному вопросу, то можно встретить упоминания мощности, рабочего напряжения, погрешности.
Номинал резистора – это величина его электрического сопротивления, основной параметр радиодетали. Разберемся, какими бывают его значения.
Резисторы имеют строго определенные, стандартные величины сопротивлений. Чем это вызвано?
Во-первых
, невозможно предусмотреть все. В зависимости от схемы требуются элементы с самыми разными параметрами. По понятной причине выпускать детали, отличающиеся по сопротивлению на доли Ом, нереально и бессмысленно. Имея их в количестве нескольких штук с отличными номиналами и зная законы электротехники, несложно подобрать и соединить образцы так, чтобы суммарное сопротивление было равно требуемому значению.
По понятной причине выпускать детали, отличающиеся по сопротивлению на доли Ом, нереально и бессмысленно. Имея их в количестве нескольких штук с отличными номиналами и зная законы электротехники, несложно подобрать и соединить образцы так, чтобы суммарное сопротивление было равно требуемому значению.
Во-вторых
, есть такое понятие – разброс параметров, или как говорят, допустимое отклонение от номинала. Это связано с неизбежными технологическими погрешностями в процессе производства. Если коротко, то резистор сначала изготавливается, а потом тестируется. По результатам испытаний наносится маркировка. То есть если допуск ± 10%, и имеется сопротивление на 100 кОм, какой смысл выпускать аналог на 95, 102 или 107? У данного образца, с учетом возможных отклонений, этот параметр лежит в пределах от 90 до 110.
Следовательно, понятно, почему номиналы всех резисторов составляют определенный ряд, с градацией по величинам сопротивлений.
Обозначение резисторов на схеме.

Давайте рассмотрим обозначение резисторов на схемах
. Существуют два возможных варианта:
Кроме того, используются немного измененные символы, которые характеризуют резисторы на схеме по величине номинальной мощности рассеивания
. Тут возникает вполне закономерный вопрос — а что это за параметр такой — номинальная мощность рассеивания? При протекании тока через резистор в нем будет выделяться , что приведет к нагреву резистора. И если мощность будет превышать допустимую величину, то резистор будет перегреваться и просто сгорит. Таким образом, номинальная рассеиваемая мощность — это величина мощности, которая может рассеиваться резистором без превышения предельно допустимой температуры. То есть если мощность в цепи будет меньше или равна номинальной, то с резистором все будет в порядке Итак, вернемся к обозначению резисторов:
Вот так обозначаются наиболее часто встречающиеся на схемах резисторы в зависимости от их номинальной рассеиваемой мощности, тут даже особо нечего дополнительно комментировать =)
Сопротивление резистора
на схемах указывается рядом с условным обозначением, причем единицу измерения обычно опускают. Если увидите на схеме рядом с резистором число 68, то не сомневайтесь ни секунды — сопротивление резистора равно 68 Омам. Если же величина сопротивления составляет, к примеру, 1500 Ом (1,5 КОм), то на схеме будет обозначение «1.5 К»:
Если увидите на схеме рядом с резистором число 68, то не сомневайтесь ни секунды — сопротивление резистора равно 68 Омам. Если же величина сопротивления составляет, к примеру, 1500 Ом (1,5 КОм), то на схеме будет обозначение «1.5 К»:
С этим все просто… Несколько сложнее ситуация обстоит с цветовой маркировкой резисторов. Сейчас мы разберемся и с этим моментом
Ряд номиналов резисторов
Номиналы резисторов представлены так называемыми рядами сопротивлений. Для постоянных резисторов имеется шесть рядов номиналов резисторов: Е6, Е12, Е24, Е48, Е96 и Е192, а для переменных сопротивлений установлен всего один ряд Е6.
Ряд номиналов резисторов Е6, Е12, Е24 соответствуют числам в таблице выше. А для номиналов сопротивлений Е48, Е96, Е192, актуальна таблица ниже:
| Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 | Е48 | Е96 | Е192 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 100 | 100 | 147 | 147 | 147 | 215 | 215 | 215 | 316 | 316 | 316 |
| 101 | 149 | 218 | 320 | ||||||||
| 102 | 102 | 150 | 150 | 221 | 221 | 324 | 324 | ||||
| 104 | 152 | 223 | 328 | ||||||||
| 105 | 105 | 105 | 154 | 154 | 154 | 226 | 226 | 226 | 332 | 332 | 332 |
| 106 | 156 | 229 | 336 | ||||||||
| 107 | 107 | 158 | 158 | 232 | 232 | 340 | 340 | ||||
| 109 | 160 | 234 | 344 | ||||||||
| 110 | 110 | 110 | 162 | 162 | 162 | 237 | 237 | 237 | 348 | 348 | 348 |
| 111 | 164 | 240 | 352 | ||||||||
| 113 | 113 | 165 | 165 | 243 | 243 | 357 | 357 | ||||
| 114 | 167 | 246 | 361 | ||||||||
| 115 | 115 | 115 | 169 | 169 | 169 | 249 | 249 | 249 | 365 | 365 | 365 |
| 117 | 172 | 252 | 370 | ||||||||
| 118 | 118 | 174 | 174 | 255 | 255 | 374 | 374 | ||||
| 120 | 176 | 258 | 379 | ||||||||
| 121 | 121 | 121 | 178 | 178 | 178 | 261 | 261 | 261 | 383 | 383 | 383 |
| 123 | 180 | 264 | 388 | ||||||||
| 124 | 124 | 182 | 182 | 267 | 267 | 392 | 392 | ||||
| 126 | 184 | 271 | 397 | ||||||||
| 127 | 127 | 127 | 187 | 187 | 187 | 274 | 274 | 274 | 402 | 402 | 402 |
| 129 | 189 | 277 | 407 | ||||||||
| 130 | 130 | 191 | 191 | 280 | 280 | 412 | 412 | ||||
| 132 | 193 | 284 | 417 | ||||||||
| 133 | 133 | 133 | 196 | 196 | 196 | 287 | 287 | 287 | 422 | 422 | 422 |
| 135 | 198 | 291 | 427 | ||||||||
| 137 | 200 | 200 | 294 | 294 | 432 | 432 | |||||
| 138 | 203 | 298 | 437 | ||||||||
| 140 | 140 | 140 | 205 | 205 | 205 | 301 | 301 | 301 | 442 | 442 | 442 |
| 142 | 208 | 305 | 448 | ||||||||
| 143 | 143 | 210 | 210 | 309 | 309 | 453 | 453 | ||||
| 145 | 213 | 312 | 459 |
Ряд номиналов конденсаторов |
Номиналы конденсаторов практически идентичны номиналам сопротивлений. В основном используемые ряды номиналов конденсаторов при производстве — ряд Е3 (в настоящее время не используется, но может такая деталька попасть из СССР запасов), Е6 и Е12, т.к. многие типы конденсаторов сложно изготовить с более высокой точностью.
В основном используемые ряды номиналов конденсаторов при производстве — ряд Е3 (в настоящее время не используется, но может такая деталька попасть из СССР запасов), Е6 и Е12, т.к. многие типы конденсаторов сложно изготовить с более высокой точностью.
Самая первая таблица этой статьи как раз актуальная для ряда номиналов конденсаторов
Что это такое
Ряд номиналов — это типовые значения номинальных величин радиоэлектронных компонентов. Кроме величины они определяют и допустимые отклонения для этой группы деталей. Стандартизация величин сопротивлений, емкостей и индуктивности для производимой промышленным образом продукции нужна для соответствия продукции выпускаемой в разных странах.
Ряд номиналов обозначается латинской буквой E и цифрами. Цифры отражают количество номинальных величин сопротивлений резисторов, емкости конденсаторов или индуктивности катушек в нём. Например, в E3 – 3 величины, а E24 – соответственно 24.
Буква E значит, что он соответствует стандартам EIA (Electronic Industries Alliance).
Начало процесса стандартизации было положено еще в 1948 году на Техническом Комитете №12 «Радиосвязь», когда был приведены значения номиналов близкие к E12. И уже в 1950 были разработаны E6, E12, E24. В итоге было принято всего 7 рядов стандартных величин и допусков отклонения (погрешностей) от них. Для чего это нужно?
Допустим в E6 есть цифра «1,0» значит все резисторы должны иметь сопротивление в долях от этого числа (если его разделить) или умноженные на 10n. Например:
1,0*102=100
Это значит, что может быть резистор на 100 Ом. Следующая в наборе цифра – «1,5». То есть элемента на 120 Ом в наборе величин E6 не бывает, может быть уже на 150 Ом. Почему это сделано?
Как мы уже упомянули, к каждому ряду привязаны определенные допуски, у E6 это ±20%, значит, что сопротивление у «100 Омного» резистора в этом случае может быть от 80 до 120 Ом. Чтобы «развести» подальше эти значения друг от друга и был выбран определенный шаг.
Шаг выбирается тоже не произвольно, набор номиналов является таблицей десятичных логарифмов, вычислить значение любого члена ряда можно по формуле:
где n – номер члена, а N – номер ряда (E3, E6 и т. д.).
д.).
Давайте разберемся с этим вопросом подробнее.
Конденсаторы
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов, это когда один из контактов всех конденсаторов соединен в одну общую точку, а другой контакт всех конденсаторов соединен в другую общую точку. При этом между пластинами каждого конденсатора будет одна и та же разность потенциала, так как все они заряжаются от общего источника.
Общая емкость всех конденсаторов при параллельном подключении будет равна сумме всех емкостей конденсаторов, так как общее количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы.
Последовательное и параллельное соединение конденсаторов
Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели.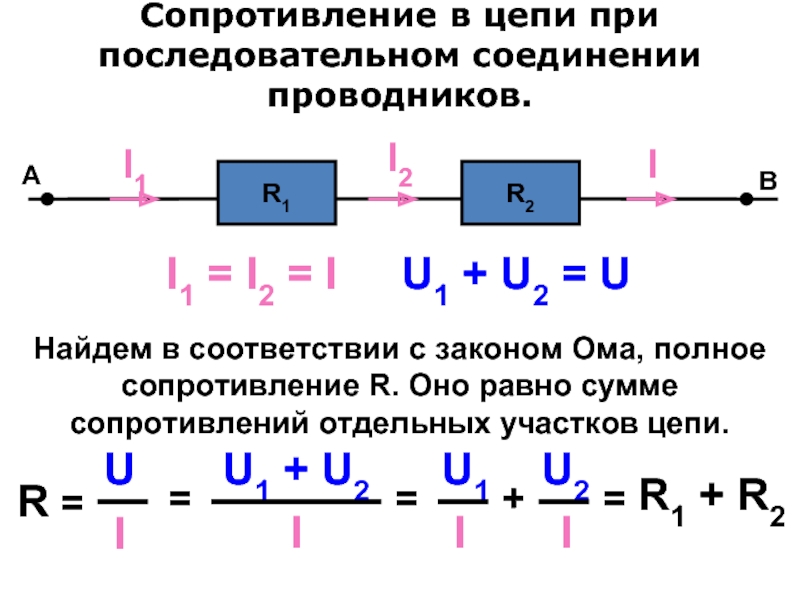 При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов.
Емкость набора при последовательном соединении конденсаторов будет вычисляться по формуле:
| 1 | = | 1 | + | 1 | + | 1 | + … | |
| C | C1 | C2 | C3 |
А общее напряжение будет равняться сумме напряжений всех конденсаторов.

Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый. При их последовательном соединении общий конденсатор будет иметь следующие данные: 10 мкФ x 300 В.
При параллельном соединении общая емкость конденсаторов складывается, а допустимое напряжение всего набора будет равно напряжению конденсатора, имеющего самое низкое значение допустимого напряжения из всего набора.
C = C1 + C2 + C3 + C4 + …Например: мы имеем три конденсатора 30 мкФ x 100 В, соединённые параллельно. Параметры всего набора конденсаторов в этом случае будут следующие: 90 мкФ x 100 В.
Соединение более двух конденсаторов последовательно редко встречается в реальных схемах. Хотя для увеличения общего напряжения такой набор может встретиться в высоковольтных источниках питания. А вот в низковольтных источниках довольно часто встречается параллельное соединение нескольких конденсаторов для сглаживания пульсаций после выпрямления при больших токах потребления.
Обратите внимание, формулы вычисления емкости последовательного и параллельного соединения конденсаторов в точности обратны формулам вычисления сопротивления при последовательном и параллельном соединении резисторов.
Расчёт шунтирующего сопротивления амперметра. Супер онлайн калькулятор. :: АвтоМотоГараж
Для контроля величины тока применяется прибор называемый амперметром. Из практики могу сказать, что не всегда под рукой оказывается прибор с нужным диапазоном измерения. Как правило, диапазон либо мал, либо велик. Здесь мы разберем, как изменить рабочий диапазон амперметра. Амперметры на большие токи от 20 ампер и выше имеют в своём составе внешний шунтирующий резистор. Он подключается параллельно амперметру. На рисунке 1 приведена схема включения амперметра с шунтирующем резистором.
В качестве примера в экспериментах будет использован амперметр M367 со шкалой до 150 ампер, соответственно при таком токе амперметр используется с внешним шунтирующим сопротивлением.
Если убрать шунтирующий резистор, то амперметр станет миллиамперметром с максимальным током отклонения стрелки 30 мА (далее будет пояснение, откуда это значение взялось). Таким образом, используя разные шунтирующие сопротивления можно сделать амперметр практически с любым диапазоном измерения.
Таким образом, используя разные шунтирующие сопротивления можно сделать амперметр практически с любым диапазоном измерения.
Рассмотрим подробнее имеющийся измерительный прибор. Из его маркировок можно узнать следующее. Маркировка в верхнем правом углу (цифра 1 на изображении). Модель измерительной головки М367. Сделан на краснодарском заводе измерительных приборов (это можно определить по ромбику с буковками ЗИП). Год выпуска 1973. Серийный номер 165266.
Маркировка в нижнем левом углу (цифра 2 на изображении). Слева на право. Прибор предназначен для измерения постоянного тока. Магнитоэлектрический прибор с подвижной рамкой. Напряжение между корпусом и мангнитоэлектрической системой не должно превышать 2 КВ. Рабочее положение шкалы прибора вертикальное. Класс точности прибора в процентах 1,5. ГОСТ8711-60. Измерительная головка рассчитана на измерения силы тока до 150 ампер с использованием внешнего шунтирующего сопротивления рассчитанного на падение на нём напряжения номиналом в 75 милливольт.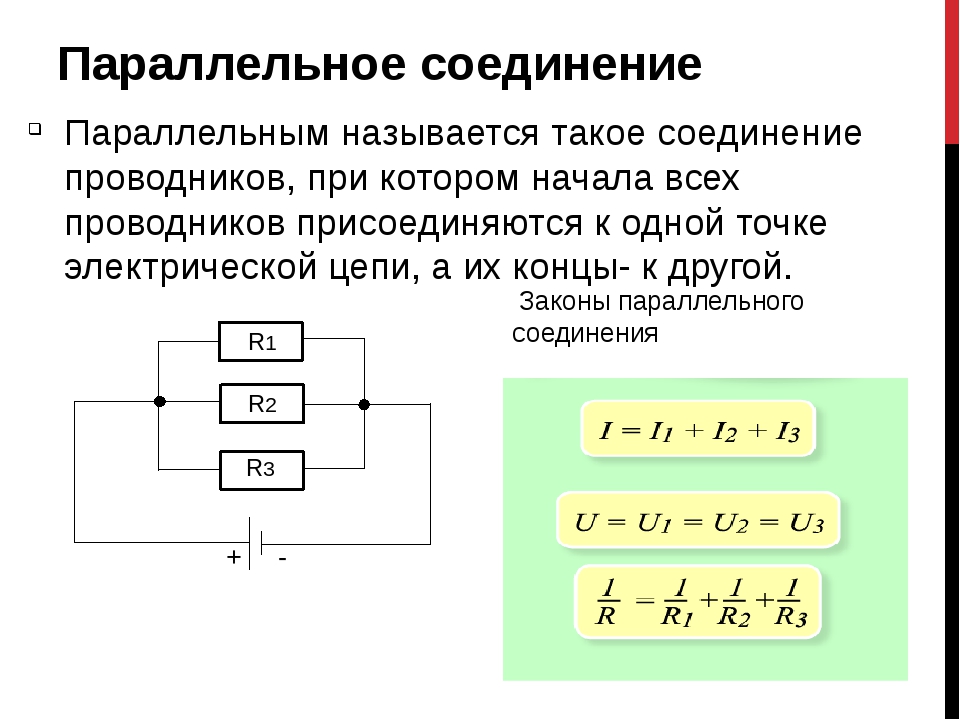
Итак, это максимум что удалось узнать из маркировки амперметра. Теперь перейдём к расчетам. Сопротивление шунта определяется по формуле:
где :
Rш — сопротивление шунтирующего резистора;
Rприб — внутреннее сопротивление амперметра;
Iприб — максимально измеримый ток амперметром без шунта;
Iраб — максимально измеримый ток с шунтом (требуемое значение)
Если все данные для расчёта имеются, то можно приступать к самому расчёту. Для упрощения можно воспользоваться онлайн калькулятором ниже:
В нашем случае из формулы видно, что данных не достаточно. Нам известен только максимальный измеряемый ток с шунтом. То есть, то, что мы хотим видеть в случае максимального отклонения стрелки амперметра.
Из маркировки прибора удалось узнать падение напряжения на шунтирующем сопротивлении. И это уже что-то. Из этого параметра ясно, что при подаче на прибор напряжения номиналом 0,075 вольт (75мВ) стрелка отклониться до крайнего значения на шкале 150 ампер. Таким образом, получается, что максимальное отклонение стрелки прибора достигается подачей напряжения 75 мВ. Вроде как данных для расчета по-прежнему не хватает. Необходимо узнать сопротивление прибора и ток, при котором стрелка откланяется до максимального значения без шунтирующего резистора. Далее предлагаю несколько способов для определения нужных параметров и решения задачи.
Таким образом, получается, что максимальное отклонение стрелки прибора достигается подачей напряжения 75 мВ. Вроде как данных для расчета по-прежнему не хватает. Необходимо узнать сопротивление прибора и ток, при котором стрелка откланяется до максимального значения без шунтирующего резистора. Далее предлагаю несколько способов для определения нужных параметров и решения задачи.
Способ первый. При помощи блока питания выясняем максимальное отклонение стрелки по току и напряжению без шунта. В нашем случае напряжение уже известно. Его замерять не будем. Измеряем ток и отклонение стрелки. Так как блока питания под рукой не оказалось, то пришлось воспользоваться очень разряженой батарейкой типа АА. Ток, который батарейка могла ещё отдать, составил 12 мА (по показаниям мультиметра). При этом токе стрелка прибора отклонилась до значения на циферблате 60А. Далее определяем цену деления и рассчитываем полное (максимальное) отклонение стрелки. Поскольку шкала циферблата амперметра размечена равномерно, то не составит труда узнать (рассчитать) ток максимального отклонения стрелки.
Цена деления прибора рассчитывается по формуле:
где:
х1 – меньшее значение,
х2 – большее значение,
n – количество промежутков (отрезков) между значениями
Для упрощения можно воспользоваться онлайн калькулятором ниже:
Расчёт показал, что цена деления прибора штатной шкалы составляет 5 ампер. При токе 12 мА стрелка отклонялась до показания 60А. Таким образом, цена одного деления без шунта составляет 1 мА. Всего делений 30, соответственно максимальное отклонение стрелки до значения 150А без шунта составляет 30 мА.
Далее при помощи закона Ома находим сопротивление прибора. 0,075/0,03=2,5 Ом
Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(10-0,03)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(5-0,03)=0,01509 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(3-0,03)=0,02525 Ом для шкалы 3А мах
Для упрощения можно воспользоваться онлайн калькулятором расчёта сопротивления шунтирующего сопротивления выше.
Второй вариант. При помощи прецизионного мультиметра замеряем сопротивление амперметра и далее при помощи закона Ома (зная напряжение максимального отклонения стрелки) находим ток максимального отклонения стрелки. Измерения выполнялись прецизионными мультиметрами Mastech MS8218 и Uni-t UT71E. При измерении сопротивления амперметра значение составило 2,50-2,52 Ом прибором UT71E и 2,52-2,53 прибором MS8218.
Формула для расчёта тока отклонения стрелки до максимального значения:
Расчёт: 0.075/2.52=0.02976А
Для упрощения вычислений максимального тока отклонения стрелки амперметра можно воспользоваться калькулятором ниже:
Далее, как и в первом варианте выполняем расчёт сопротивления шунтирующего резистора (калькулятор выше). Для расчёта было принято среднее показание измеренного сопротивления амперметра двумя мультиметрами Rприб = 2,52Ом
Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(10-0,02976)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(5-0,02976)=0,01508 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(3-0,02976)=0,02524 Ом для шкалы 3А мах
Если сравнить расчёты двух методик между собой, то получились совпадение данных до четвёртого знака после запятой, а в некоторых случаях даже до пяти знаков.
О тонкостях изготовления шунтирующего сопротивления расскажу в следующей статье: Как сделать шунт (шунтирующий резистор) для амперметра. Самый простой метод подбора.
И ещё одно продолжение этой тематики: Как изменить предел измерения амперметра. Как переделать амперметр постоянного тока на переменный.
Расчет сопротивления резистора для блока питания. Калькулятор расчета сопротивления для светодиодов
Светодиод – это полупроводниковый элемент , который применяется для освещения. Применяется в фонарях, лампах, светильниках и других осветительных приборах. Принцип его работы заключается в том, что при протекании тока через светоизлучающий диод происходит высвобождение фотонов с поверхности материала полупроводника, и диод начинает светиться. Надежная работа светодиода зависит от тока , протекающего через него. При заниженных значениях, он просто не будет светить, а при превышении значения тока – характеристики элемента ухудшатся, вплоть до его разрушения. При этом говорят – светодиод сгорел. Для того чтобы исключить возможность выхода из строя этого полупроводника необходимо подобрать в цепь с включенным в нее, резистором. Он будет ограничивать ток в цепи на оптимальных значениях.
При этом говорят – светодиод сгорел. Для того чтобы исключить возможность выхода из строя этого полупроводника необходимо подобрать в цепь с включенным в нее, резистором. Он будет ограничивать ток в цепи на оптимальных значениях.
Для работы радиоэлемента на него нужно подать питание. По закону Ома , чем больше сопротивление отрезка цепи, тем меньший ток по нему протекает. Опасная ситуация возникает, если в схеме течет больший ток, чем положено, так как каждый элемент не выдерживает большей токовой нагрузки.
Сопротивление светодиода является нелинейным. Это значит, что при изменении напряжения, подаваемого на этот элемент, ток, протекающий через него, будет меняться нелинейно. Убедиться в этом можно, если найти вольт — амперную характеристику любого диода, в том числе и светоизлучающего. При подаче питания ниже напряжения открытия p — n перехода, ток через светодиод низкий, и элемент не работает. Как только этот порог превышен, ток через элемент стремительно возрастает, и он начинает светиться.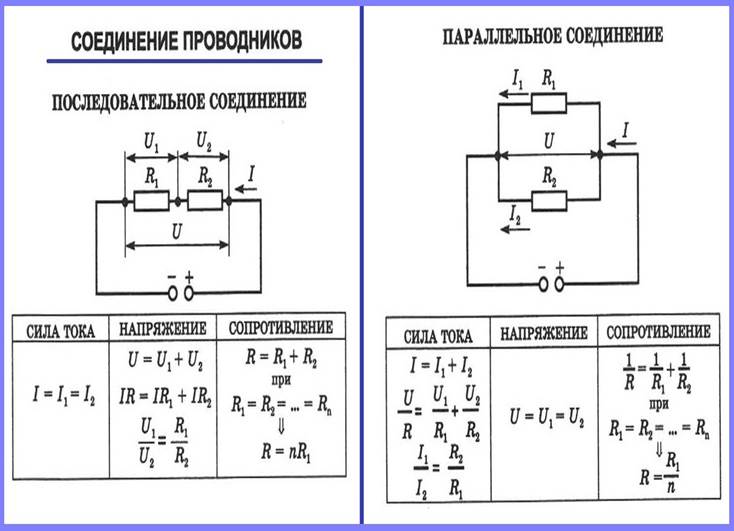
Если источник питания соединять непосредственно со светодиодом, диод выйдет из строя, так как не рассчитан на такую нагрузку. Чтобы этого не произошло – нужно ограничить ток, протекающий через светодиод балластным сопротивлением, или произвести понижение напряжения на важном для нас полупроводнике.
Рассмотрим простейшую схему подключения (рисунок 1). Источник питания постоянного тока подключается последовательно через резистор к нужному светодиоду, характеристики которого нужно обязательно узнать. Сделать это можно в интернете, скачав описание (информационный лист) на конкретную модель, или найдя нужную модель в справочниках. Если найти описание не представляется возможным, можно приблизительно определить падение напряжения на светодиоде по его цвету:
- Инфракрасный — до 1.9 В.
- Красный – от 1.6 до 2.03 В.
- Оранжевый – от 2.03 до 2.1 В.
- Желтый – от 2.1 до 2.2 В.
- Зеленый – от 2.2 до 3.5 В.
- Синий – от 2.5 до 3.7 В.
- Фиолетовый – 2.
 8 до 4 В.
8 до 4 В. - Ультрафиолетовый – от 3.1 до 4.4 В.
- Белый – от 3 до 3.7 В.
Рисунок 1 – схема подключения светодиода
Ток в схеме можно сравнить с движением жидкости по трубе. Если есть только один путь протекания, то сила тока (скорость течения) во всей цепи будет одинакова. Именно так происходит в схеме на рисунке 1. Согласно закону Кирхгоффа, сумма падений напряжения на всех элементах, включенных в цепь протекания одного тока, равно ЭДС этой цепи (на рисунке 1 обозначено буквой Е). Отсюда можно сделать вывод, что напряжение, падающее на токоограничивающем резисторе должно быть равным разности напряжения питания и падения его на светодиоде.
Так как ток в цепи должен быть одинаковым, то и через резистор, и через светодиод ток получается одним и тем же. Для стабильной работы полупроводникового элемента, увеличения его показателей надежности и долговечности, ток через него должен быть определенных значений, указанных в его описании. Если описание найти невозможно, можно принять приблизительное значение тока в цепи 10 миллиампер. После определения этих данных уже можно вычислить номинал сопротивления резистора для светодиода. Он определяется по закону Ома. Сопротивление резистора равно отношению падения напряжения на нем к току в цепи. Или в символьной форме:
После определения этих данных уже можно вычислить номинал сопротивления резистора для светодиода. Он определяется по закону Ома. Сопротивление резистора равно отношению падения напряжения на нем к току в цепи. Или в символьной форме:
R = U (R)/ I ,
где, U (R) — падение напряжения на резисторе
I – ток в цепи
Расчет U (R) на резисторе:
U (R) = E – U (Led)
где, U (Led) — падение напряжения на светодиодном элементе.
С помощью этих формул получится точное значение сопротивления резистора. Однако, промышленностью выпускаются только стандартные значения сопротивлений так называемые ряды номиналов. Поэтому после расчета придется сделать подбор существующего номинала сопротивления. Подобрать нужно чуть больший резистор, чем получилось в расчете, таким образом, получится защита от случайного превышения напряжения в сети. Если подобрать близкий по значению элемент сложно, можно попробовать соединить два резистора последовательно, или параллельно.
Если подобрать сопротивление меньшей мощности, чем нужно в схеме, оно просто выйдет из строя. Расчет мощности резистора довольно прост, нужно падение напряжения на нём умножить на ток, протекающий в этой цепи. После чего нужно выбрать сопротивление с мощностью, не меньшей рассчитанной.
Пример расчета
Имеем напряжение питания 12В, зеленый светодиод. Нужно рассчитать сопротивление и мощность токоограничивающего резистора. Падение напряжения на нужном нам зеленом светодиоде равно 2,4 В, номинальный ток 20 мА. Отсюда вычисляем напряжение, падающее на балластном резисторе.
U (R) = E – U (Led) = 12В – 2,4В = 9,6В.
Значение сопротивления:
R = U (R)/ I = 9,6В/0,02А = 480 Ом.
Значение мощности:
P = U (R) ⋅ I = 9,6В ⋅ 0,02А = 0,192 Вт
Из ряда стандартных сопротивлений выбираем 487 Ом (ряд Е96), а мощность можно выбрать 0,25 Вт. Такой резистор нужно заказать.
В том случае, если нужно подключить несколько светодиодов последовательно, подключать их к источнику питания можно также с помощью только одного резистора, который будет гасить избыточное напряжение. Его расчет производится по указанным выше формулам, однако, вместо одного прямого напряжения U (Led) нужно взять сумму прямых напряжений нужных светодиодов.
Его расчет производится по указанным выше формулам, однако, вместо одного прямого напряжения U (Led) нужно взять сумму прямых напряжений нужных светодиодов.
Если требуется подключить несколько светоизлучающих элементов параллельно, то для каждого из них требуется рассчитать свой резистор, так как у каждого из полупроводников может быть свое прямое напряжение. Вычисления для каждой цепи в таком случае аналогичны расчету одного резистора, так как все они подключаются параллельно к одному источнику питания, и его значение для расчета каждой цепи одно и то же.
Этапы вычисления
Чтобы сделать правильные вычисления, необходимо выполнить следующее:
- Выяснение прямого напряжения и тока светодиода.
- Расчет падения напряжения на нужном резисторе.
- Расчет сопротивления резистора.
- Подбор сопротивления из стандартного ряда.
- Вычисление и подбор мощности.
Этот несложный расчет можно сделать самому, но проще и эффективнее по времени воспользоваться калькулятором для расчета резистора для светодиода. Если ввести такой запрос в поисковик, найдется множество сайтов, предлагающих автоматизированный подсчет. Все необходимые формулы в этот инструмент уже встроены и работают мгновенно. Некоторые сервисы сразу предлагают также и подбор элементов. Нужно будет только выбрать наиболее подходящий калькулятор для расчета светодиодов, и, таким образом, сэкономить свое время.
Если ввести такой запрос в поисковик, найдется множество сайтов, предлагающих автоматизированный подсчет. Все необходимые формулы в этот инструмент уже встроены и работают мгновенно. Некоторые сервисы сразу предлагают также и подбор элементов. Нужно будет только выбрать наиболее подходящий калькулятор для расчета светодиодов, и, таким образом, сэкономить свое время.
Калькулятор светодиодов онлайн – не единственное средство для экономии времени в вычислениях. Расчет транзисторов, конденсаторов и других элементов для различных схем уже давно автоматизирован в интернете. Остается только грамотно воспользоваться поисковиком для решения этих задач.
Светодиоды – оптимальное решение для многих задач освещения дома, офиса и производства. Обратите внимание на светильники Ledz. Это лучшее соотношение цены и качества осветительной продукции, используя их, вам не придется самим делать расчеты и собирать светотехнику.
#s3gt_translate_tooltip_mini { display: none !important; }
В схемах со светодиодами обязательно используются для ограничения. Они защищают от перегорания и преждевременного выхода из строя светодиодных элементов. Основная проблема заключается в точном подборе необходимых параметров, поэтому у специалистов широкой популярностью пользуется калькулятор расчета сопротивления для светодиодов. Для получения максимально точных результатов потребуются данные о напряжении источника питания, о прямом напряжении самого светодиода и его расчетном токе, а также схема подключения и количество элементов.
Они защищают от перегорания и преждевременного выхода из строя светодиодных элементов. Основная проблема заключается в точном подборе необходимых параметров, поэтому у специалистов широкой популярностью пользуется калькулятор расчета сопротивления для светодиодов. Для получения максимально точных результатов потребуются данные о напряжении источника питания, о прямом напряжении самого светодиода и его расчетном токе, а также схема подключения и количество элементов.
Как рассчитать сопротивление токоограничивающих резисторов
В самом простом случае, когда отсутствуют необходимые исходные данные, величину прямого напряжения светодиодов можно с высокой точностью установить по цвету свечения. Типовые данные об этом физическом явлении сведены в таблицу.
Многие светодиоды имеют расчетный ток 20 мА. Существуют и другие виды элементов, у которых этот параметр может достигать значения 150 мА и выше. Поэтому для того чтобы точно определить номинальный ток, понадобятся данные о технических характеристиках светодиода. Если же нужная информация полностью отсутствует, номинальный ток элемента условно принимается за 10 мА, а прямое напряжение — 1,5-2 вольта.
Если же нужная информация полностью отсутствует, номинальный ток элемента условно принимается за 10 мА, а прямое напряжение — 1,5-2 вольта.
Количество токоограничивающих резисторов напрямую зависит от схемы подключения полупроводниковых элементов. Например, если используется , можно вполне обойтись одним резистором, поскольку сила тока во всех точках будет одинаковой.
В случае параллельного соединения одного гасящего резистора будет уже недостаточно. Это связано с тем, что характеристики светодиодов не могут быть абсолютно одинаковыми. Все они обладают собственными сопротивлениями и такими же разными потребляемыми токами. То есть, элемент с минимальным сопротивлением потребляет большее количество тока и может преждевременно выйти из строя.
Следовательно, если выйдет из строя хотя-бы один светодиод из подключенных параллельно, это приведет к возникновению повышенного напряжения, на которое остальные элементы не рассчитаны. В результате, они тоже перестанут работать.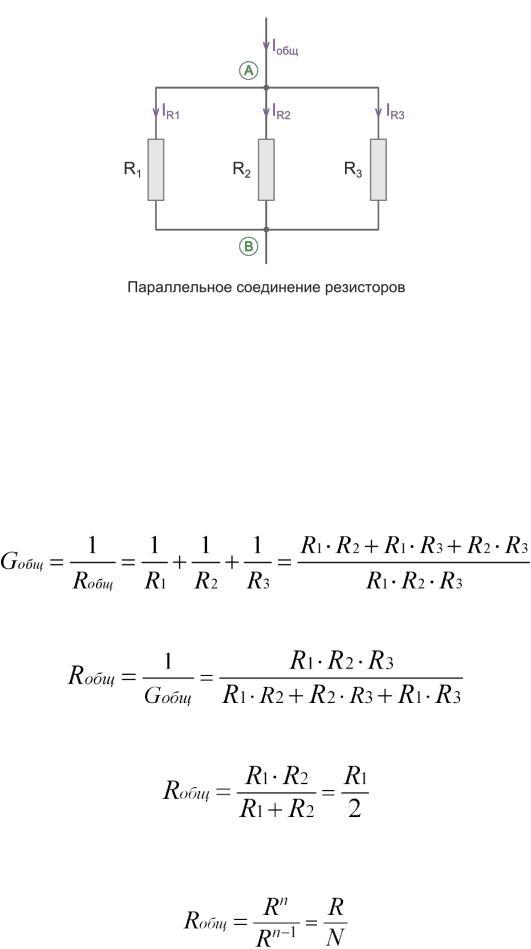 Поэтому при параллельном соединении для каждого светодиода предусматривается собственный резистор.
Поэтому при параллельном соединении для каждого светодиода предусматривается собственный резистор.
Все эти особенности учтены в онлайн-калькуляторе. В основе расчетов лежит формула определения сопротивления: R = Uгасящее/Iсветодиода. В свою очередь Uгасящее = Uпитания — Uсветодиода.
При подключении светодиодов небольшой мощности чаще всего используется гасящий резистор. Это наиболее простая схема подключения, которая позволяет получить требуемую яркость без использования дорогостоящих . Однако, при всей ее простоте, для обеспечения оптимального режима работы необходимо провести расчет резистора для светодиода.
Светодиод как нелинейный элемент
Рассмотрим семейство вольт-амперных характеристик (ВАХ) для светодиодов различных цветов:
Эта характеристика показывает зависимость тока, проходящего через светоизлучающий диод, от напряжения, приложенного к нему.
Как видно на рисунке, характеристики имеют нелинейный характер. Это означает, что даже при небольшом изменении напряжения на несколько десятых долей вольта, ток может измениться в несколько раз.
Однако при работе со светодиодами обычно используют наиболее линейный участок (т.н. рабочую область) ВАХ, где ток изменяется не так резко. Чаще всего производители указывают в характеристиках светодиода положение рабочей точки, то есть значения напряжения и тока, при которых достигается заявленная яркость свечения.
На рисунке показаны типовые значения рабочих точек для красных, зеленых, белых и голубых светодиодов при токе 20 мА. Здесь можно заметить, что led разных цветов при одинаковом токе имеют разное падение напряжения в рабочей области. Эту особенность следует учитывать при проектировании схем.
Представленные выше характеристики были получены для светоизлучающих диодов, включенных в прямом направлении. То есть отрицательный полюс питания подключен к катоду, а положительный – к аноду, как показано на картинке справа:
Полная же ВАХ выглядит следующим образом:
Здесь видно, что обратное включение бессмысленно, поскольку светодиод не будет излучать, а при превышении некоторого порога обратного напряжения выйдет из строя в результате пробоя. Излучение же происходит только при включении в прямом направлении, причем интенсивность свечения зависит от тока, проходящего через led. Если этот ток ничем не ограничивать, то led перейдет в область пробоя и перегорит. Если нужно установить рабочий светодиод или нет, то Вам будет полезна статья подробно раскрывающая все способы .
Излучение же происходит только при включении в прямом направлении, причем интенсивность свечения зависит от тока, проходящего через led. Если этот ток ничем не ограничивать, то led перейдет в область пробоя и перегорит. Если нужно установить рабочий светодиод или нет, то Вам будет полезна статья подробно раскрывающая все способы .
Как подобрать резистор для одиночного светодиода
Для ограничения тока светоизлучающего диода можно использовать резистор, включенный таким образом:
Теперь определяем, какой резистор нужен. Для расчета сопротивления используется формула:
где U пит — напряжение питания,
U пад- падение напряжения на светодиоде,
I — требуемый ток светодиода.
При этом мощность, рассеиваемая на резисторе, будет пропорциональна квадрату тока:
Например, для красного светодиода Cree C503B-RAS типовое падение напряжения составляет 2.1 В при токе 20 мА. При напряжении питания 12 В сопротивление резистора будет составлять
Из стандартного ряда сопротивлений Е24 подбираем наиболее близкое значение номинала – 510 Ом. Тогда мощность, рассеиваемая на резисторе, составит
Тогда мощность, рассеиваемая на резисторе, составит
Таким образом, потребуется гасящий резистор номиналом 510 Ом и мощностью рассеивания 0.25 Вт.
Может сложиться впечатление, что при низких напряжениях питания можно подключать led без резистора. На этом видео наглядно показано, что произойдет со светоизлучающим диодом, включенного таким образом, при напряжении всего 5 В:
Светодиод сначала будет работать, но через несколько минут просто перегорит. Это вызвано нелинейным характером его ВАХ, о чем говорилось в начале статьи.
Никогда не подключайте светодиод без гасящего резистора даже при низком напряжении питания. Это ведет к его выгоранию и, в лучшем случае, к обрыву цепи, а в худшем – к короткому замыканию.
Расчет резистора при подключении нескольких светодиодов
При последовательном соединении используется один резистор, задающий одинаковый ток всей цепочке led. При этом следует учитывать, что источник питания должен обеспечивать напряжение, превышающее общее падение напряжения на диодах. То есть при соединении 4 светодиодов с падением 2.5 В потребуется источник напряжением более 10 В. Ток при этом для всех будет одинаковым. Сопротивление резистора в этом случае можно рассчитать по формуле:
То есть при соединении 4 светодиодов с падением 2.5 В потребуется источник напряжением более 10 В. Ток при этом для всех будет одинаковым. Сопротивление резистора в этом случае можно рассчитать по формуле:
где — напряжение питания,
— сумма падений напряжения на светодиодах,
— ток потребления.
Так, 4 зеленых светодиода Kingbright L-132XGD напряжением 2.5 В и током 10 мА при питании 12 В потребуют резистора сопротивлением
При этом он должен рассеивать мощность
При параллельном подключении каждому светоизлучающему диоду ток ограничивает свой резистор. В таком случае можно использовать низковольтный источник питания, но ток потребления всей цепи будет складываться из токов, потребляемых каждым светодиодом. Например, 4 желтых светодиода BL-L513UYD фирмы Betlux Electronics с потреблением 20 мА каждый, потребуют от источника ток не менее 80 мА при параллельном включении. Здесь сопротивление и мощность резисторов для каждой пары «резистор – led» рассчитываются так же, как при подключении одиночного светодиода.
Обратите внимание, что и при последовательном, и при параллельном соединении используются источники питания одинаковой мощности. Только в первом случае потребуется источник с большим напряжением, а во втором – с большим током.
Нельзя подключать параллельно несколько светодиодов к одному резистору, т.к. либо они все будут гореть очень тускло, либо один из них может открыться чуть раньше других, и через него пойдет очень большой ток, который выведет его из строя.
Программы для расчета сопротивления
При большом количестве подключаемых led, особенно если они включены и последовательно, и параллельно, рассчитывать сопротивление каждого резистора вручную может быть проблематичным.
Проще всего в таком случае воспользоваться одной из многочисленных программ расчета сопротивления. Очень удобным в этом плане является онлайн калькулятор на сайте cxem.net:
Он включает в себя небольшую базу данных самых распространенных светодиодов, поэтому необязательно вручную набирать значения падения напряжения и тока, достаточно указать напряжение питания и выбрать из списка нужный светоизлучающий диод.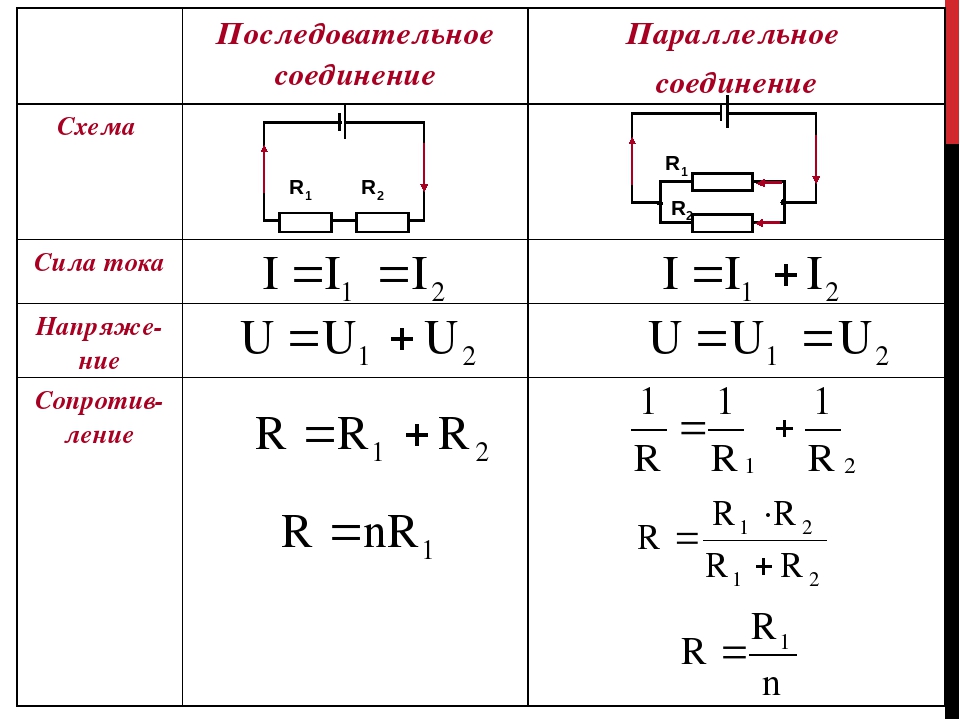 Программа рассчитает сопротивление и мощность резисторов, а также нарисует схему подключения или принципиальную схему.
Программа рассчитает сопротивление и мощность резисторов, а также нарисует схему подключения или принципиальную схему.
Например, с помощью этого калькулятора был рассчитан резистор для трех XLamp MX3 при напряжении питания 12 В:
Также программа обладает очень полезной функцией: она подскажет цветовую маркировку требуемого резистора.
Еще одна простая программа для расчета сопротивления распространенная на просторах интернета разработана Сергеем Войтевичем с портала ledz.org.
Здесь уже вручную выбирается способ подключения светодиодов, напряжение и ток. Программа не требует установки, достаточно распаковать ее в любую директорию.
Заключение
Гасящий резистор – самый простой ограничитель тока для светодиодной цепи. От его подбора зависит ток, а значит, интенсивность свечения и долговечность led. Однако следует помнить, что при больших токах на резисторе будет выделяться значительная мощность, поэтому для питания мощных светодиодов лучше применять драйверы.
Основным параметром, влияющим на долговечность светодиода, является электрический ток, величина которого строго нормируется для каждого типа LED-элемента. Одним из распространенных способов ограничения максимального тока является использование ограничительного резистора. Резистор для светодиода можно рассчитать без применения сложных вычислений на основании закона Ома, используя технические значения параметров диода и напряжение в цепи включения.
Особенности включения светодиода
Работая по одинаковому принципу с выпрямительными диодами, светоизлучающие элементы, тем не менее, имеют отличительные особенности. Наиболее важные из них:
- Крайне отрицательная чувствительность к напряжению обратной полярности. Светодиод, включенный в цепь с нарушением правильной полярности, выходит из строя практически мгновенно.
- Узкий диапазон допустимого рабочего тока через p-n переход.
- Зависимость сопротивления перехода от температуры, что свойственно большинству полупроводниковых элементов.

На последнем пункте следует остановиться подробнее, поскольку он является основным для расчета гасящего резистора. В документации на излучающие элементы указывается допустимый диапазон номинального тока, при котором они сохраняют работоспособность и обеспечивают заданные характеристики излучения. Занижение величины не является фатальным, но приводит к некоторому снижению яркости. Начиная с некоторого предельного значения, прохождение тока через переход прекращается, и свечение будет отсутствовать.
Превышение тока сначала приводит к увеличению яркости свечения, но срок службы при этом резко сокращается. Дальнейшее повышение приводит к выходу элемента из строя. Таким образом, подбор резистора для светодиода преследует цель ограничить максимально допустимый ток в наихудших условиях.
Напряжение на полупроводниковом переходе ограничено физическими процессами на нем и находится в узком диапазоне около 1-2 В. Светоизлучающие диоды на 12 Вольт, часто устанавливаемые на автомобили, могут содержать цепочку последовательно соединенных элементов или ограничительную схему, включенную в конструкцию.
Зачем нужен резистор для светодиода
Использование ограничительных резисторов при включении светодиодов является пусть и не самым эффективным, зато самым простым и дешевым решением ограничить ток в допустимых пределах. Схемные решения, которые позволяют с высокой точностью стабилизировать ток в цепи излучателей достаточно сложны для повторения, а готовые имеют высокую стоимость.
Применение резисторов позволяет выполнять освещение и подсветку своими силами. Главное при этом – умение пользоваться измерительными приборами и минимальные навыки пайки. Грамотно рассчитанный ограничитель с учетом возможных допусков и колебаний температуры способен обеспечить нормальное функционирование светодиодов в течении всего заявленного срока службы при минимальных затратах.
Параллельное и последовательное включение светодиодов
С целью совмещения параметров цепей питания и характеристик светодиодов широко распространены последовательное и параллельное соединение нескольких элементов. У каждого типа соединений есть как достоинства, так и недостатки.
У каждого типа соединений есть как достоинства, так и недостатки.
Параллельное включение
Достоинством такого соединения является использование всего одного ограничителя на всю цепь. Следует оговориться, что данное достоинство является единственным, поэтому параллельное соединение практически нигде не встречается, за исключением низкосортных промышленных изделий. Недостатки таковы:
- Мощность рассеивания на ограничительном элементе растет пропорционально количеству параллельно включенных светодиодов.
- Разброс параметров элементов приводит к неравномерности распределения токов.
- Перегорание одного из излучателей ведет к лавинообразному выходу из строя всех остальных ввиду увеличения падения напряжения на параллельно включенной группе.
Несколько увеличивает эксплуатационные свойства соединение, где ток через каждый излучающий элемент ограничивается отдельным резистором. Точнее, это является параллельным соединением отдельных цепей, состоящих из светодиодов с ограничительными резисторами. Основное достоинство – большая надежность, поскольку выход из строя одного или нескольких элементов никаким образом не отражается на работе остальных.
Основное достоинство – большая надежность, поскольку выход из строя одного или нескольких элементов никаким образом не отражается на работе остальных.
Недостатком является тот факт, что из-за разброса параметров светодиодов и технологического допуска на номинал сопротивлений яркость свечения отдельных элементов может сильно различаться. Такая схема содержит большое количество радиоэлементов.
Параллельное соединение с индивидуальными ограничителями находит применение в цепях с низким напряжением, начиная с минимального, ограниченного падением напряжения на p-n переходе.
Последовательное включение
Последовательное включение излучающих элементов получило самое широкое распространение, поскольку несомненным достоинством последовательной цепи является абсолютное равенство тока, проходящего через каждый элемент. Поскольку ток через единственный ограничительный резистор и через диод одинаков, то и рассеиваемая мощность будет минимальной.
Существенный недостаток – выход из строя хотя бы одного из элементов приведет к неработоспособности всей цепочки. Для последовательного соединения требуется повышенное напряжение, минимальное значение которого растет пропорционально количеству включенных элементов.
Для последовательного соединения требуется повышенное напряжение, минимальное значение которого растет пропорционально количеству включенных элементов.
Смешанное включение
Использование большого количества излучателей возможно при выполнении смешанного соединения, когда используют несколько параллельно включенных цепочек, и последовательного соединения одного ограничительного резистора и нескольких светодиодов.
Перегорание одного из элементов приведет к неработоспособности только одной цепи, в которой установлен данный элемент. Остальные будут функционировать исправно.
Формулы расчета резистора
Расчет сопротивления резистора для светодиодов базируется на законе Ома. Исходными параметрами для того, как рассчитать резистор для светодиода, являются:
- напряжение цепи;
- рабочий ток светодиода;
- падение напряжения на излучающем диоде (напряжение питания светодиода).
Величина сопротивления определяется из выражения:
где U – падение напряжения на резисторе, а I – прямой ток через светодиод.
Падение напряжения светодиода определяют из выражения:
U = Uпит – Uсв,
где Uпит – напряжение цепи, а Uсв – паспортное падение напряжения на излучающем диоде.
Расчет светодиода для резистора дает значение сопротивления, которое не будет находиться в стандартном ряду значений. Брать нужно резистор с сопротивлением, ближайшим к вычисленному значению с большей стороны. Таким образом учитывается возможное увеличение напряжения. Лучше взять значение, следующее в ряду сопротивлений. Это несколько уменьшит ток через диод и снизит яркость свечения, но при этом нивелируется любое изменение величины питающего напряжения и сопротивления диода (например, при изменении температуры).
Перед тем как выбрать значение сопротивления, следует оценить возможное снижение тока и яркости по сравнению с заданным по формуле:
(R – Rст)R 100%
Если полученное значение составляет менее 5%, то нужно взять большее сопротивление, если от 5 до 10%, то можно ограничиться меньшим.
Не менее важный параметр, сказывающийся на надежности работы – рассеиваемая мощность токоограничительного элемента. Ток, проходящий через участок с сопротивлением, вызывает его нагрев. Для определения мощности, которая будет рассеиваться, используют формулу:
Используют ограничивающий резистор, чья допустимая мощность рассеивания будет превосходить расчетную величину.
Имеется светодиод с падением напряжения на нем 1.7 В с номинальным током 20 мА. Необходимо включить его в цепь с напряжением 12 В.
Падение напряжения на ограничительном резисторе составляет:
U = 12 – 1.7 = 10.3 В
Сопротивление резистора:
R = 10.3/0.02 = 515 Ом.
Ближайшее большее значение в стандартном ряду составляет 560 Ом. При таком значении уменьшение тока по сравнению с заданным составляет чуть менее 10%, поэтому большее значение брать нет необходимости.
Рассеиваемая мощность в ваттах:
P = 10.3 10.3/560 = 0.19 Вт
Таким образом, для данной цепи можно использовать элемент с допустимой мощностью рассеивания 0. 25 Вт.
25 Вт.
Подключение светодиодной ленты
Светодиодные ленты выпускаются на различное напряжение питания. На ленте располагается цепь из последовательно включенных диодов. Количество диодов и сопротивление ограничительных резисторов зависят от напряжения питания ленты.
Наиболее распространенные типы светодиодных лент предназначены для подключения в цепь с напряжением 12 В. Использование для работы большего значения напряжения здесь также возможно. Для правильного расчета резисторов необходимо знать ток, идущий через единичный участок ленты.
Увеличение длины ленты вызывает пропорциональное увеличение тока, поскольку минимальные участки технологически соединены параллельно. Например, если минимальная длина отрезка составляет 50 см, то на ленту 5м из 10 таких отрезков придется возросший в 10 раз ток потребления.
Вот так светодиод выглядит в жизни:
А так обозначается на схеме:
Для чего служит светодиод?
Светодиоды
излучают свет, когда через них проходит электрический ток.
Были изобретены в 70-е года прошлого века для смены электрических лампочек, которые часто перегорали и потребляли много энергии.
Подключение и пайка
Светодиоды должны быть подключены правильным образом,
учитывая их полярность + для анода и к для катода Катод имеет короткий вывод,
более короткую ножку. Если вы видите внутри светодиода его внутренности —
катод имеет электрод большего размера (но это не официальные метод).
Светодиоды могут быть испорчены в результате
воздействия тепла при пайке, но риск невелик, если вы паяете быстро.
Никаких специальных мер предосторожности применять не надо для пайки большинства
светодиодов, однако бывает полезно ухватиться за ножку светодиода пинцетом – для
теплоотвода.
Проверка светодиодов
Никогда не
подключайте светодиодов непосредственно батарее или источнику питания!
Светодиод перегорит практически моментально, поскольку слишком
большой ток сожжет его. Светодиоды должны иметь ограничительный
резистор. Для быстрого тестирования 1кОм резистор подходит большинству
светодиодов если напряжение 12V или менее. Не забывайте подключать светодиоды
правильно, соблюдая полярность!
Для быстрого тестирования 1кОм резистор подходит большинству
светодиодов если напряжение 12V или менее. Не забывайте подключать светодиоды
правильно, соблюдая полярность!
Цвета светодиодов
Светодиоды бывают
почти всех цветов: красный, оранжевый, желтый, желтый, зеленый, синий и
белый. Синего и белого светодиода немного дороже, чем другие цвета.
Цвет светодиодов определяется типом полупроводникового материала, из
которого он сделан, а не цветом пластика его корпуса. Светодиоды любых
цветов бывают в бесцветном корпусе, в таком случае цвет можно узнать только
включив его…
Многоцветные
светодиоды
Устроен многоцветный светодиод просто, как правило
это красный и зеленый объединенные в один корпус с тремя ножками. Путём
изменения яркости или количества импульсов на каждом из кристаллов можно
добиваться разных цветов свечения.
Расчет светодиодного резистора
Светодиод должен иметь резистор последовательно соединенный в его цепи, для
ограничения тока, проходящего через светодиод, иначе он сгорит практически
мгновенно. ..
..
Резистор R определяется по формуле:
R = (V
S
— V
L
) /
I
V
S
= напряжение
питания
V
L
= прямое
напряжение, расчётное для каждого типа диодов (как правилоот 2 до
4волт)
I
= ток светодиода (например
20мA), это должно быть меньше максимально допустимого для Вашего
диода
Если размер сопротивления не получается подобрать точно, тогда
возьмите резистор большего номинала. На самом деле вы вряд-ли заметите
разницу… совсем яркость свечения уменьшится совсем
незначительно.
Например: Если напряжение питания V S = 9 В,
и есть красный светодиод (V = 2V), требующие I = 20мA = 0.020A,
R = (-
9 В) / 0.02A = 350 Ом. При этом можно выбрать 390 Ом (ближайшее стандартное
значение, которые больше).
Вычисление светодиодного резистора с использованием Закон
Ома
Закон Ома гласит, что сопротивление резистора R = V / I,
где:
V = напряжение через резистор (V = S — V L в данном случае)
I = ток через резистор
Итак R = (V
S
— V
L
) /
I
Последовательное подключение
светодиодов.
Если вы хотите подключить несколько светодиодов
сразу – это можно сделать последовательно. Это сокращает потребление энергии и
позволяет подключать большое количество диодов одновременно, например в качестве
какой-то гирлянды.
Все светодиоды, которые соединены последовательно,
долдны быть одного типа. Блок питания должен иметь достаточную мощность
и обеспечить соответствующее напряжение.
Пример расчета:
Красный, желтый и
зеленый диоды — при последовательном соединении необходимо напряжение
питания — не менее 8V, так 9-вольтовая батарея будет практически идеальным
источником.
V
L
= 2V
+ 2V + 2V = 6V (три диода, их напряжения суммируются).
Если
напряжение питания V S 9 В и ток диода = 0.015A,
Резистором R = (V S
— V L
) / I
= (9 — 6)
/0,015 = 200 Ом
Берём резистор 220 Ом (ближайшего
стандартного значения, которое больше).
Избегайте подключения светодиодов в
параллели!
Подключение несколько светодиодов в параллели
с помощью одного резистора не очень хорошая идея…
Как правило, светодиоды имеют разброс параметров,
требуют несколько различные напряжения каждый.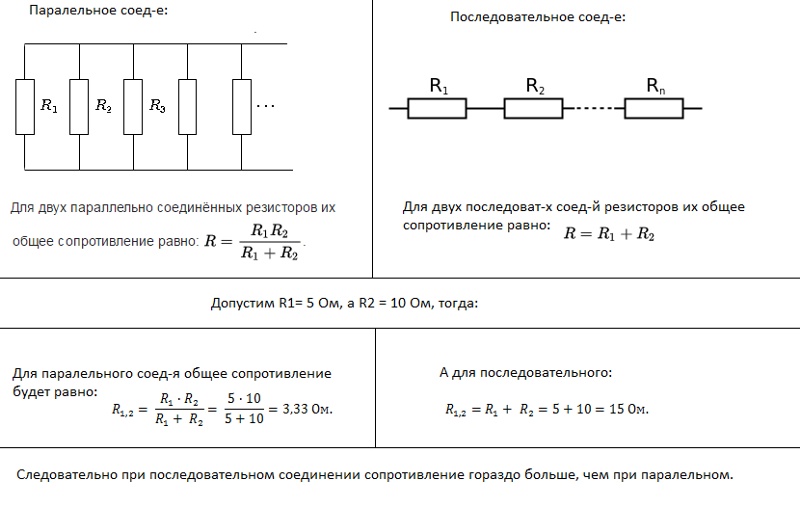 ., что делает такое подключение
практически нерабочим. Один из диодов будет светиться ярче и брать на себя тока
больше, пока не выйдет из строя. Такое подключение многократно ускоряет
естественную деградацию кристалла светодиода. Если светодиоды соединяются
параллельно, каждый из них должен иметь свой собственный ограничительный
резистор.
., что делает такое подключение
практически нерабочим. Один из диодов будет светиться ярче и брать на себя тока
больше, пока не выйдет из строя. Такое подключение многократно ускоряет
естественную деградацию кристалла светодиода. Если светодиоды соединяются
параллельно, каждый из них должен иметь свой собственный ограничительный
резистор.
Мигающие светодиоды
Мигающие
светодиоды выглядят как обычные светодиоды, они могут мигать самостоятельно
потому, что содержат встроенную интегральную схему. Светодиод мигает на
низких частотах, как правило 2-3 вспышки в секунду. Такие безделушки
делают для автомобильных сигнализаций, разнообразных индикаторов или детских
игрушек.
Цифробуквенные светодиодные индикаторы
Светодиодные цифробуквенные индикаторы сейчас применяются
очень редко, они сложнее и дороже жидкокристаллических. Раньше, это было
практически единственным и самым продвинутым средством индикации, их ставили
даже на сотовые телефоны:)
Расчет резистора для светодиода | Практическая электроника
Так как для светоизлучающего диода (СИД, LED, светодиода) весьма желательно питание стабильным током, то не стоит его подключать непосредственно к источнику напряжения.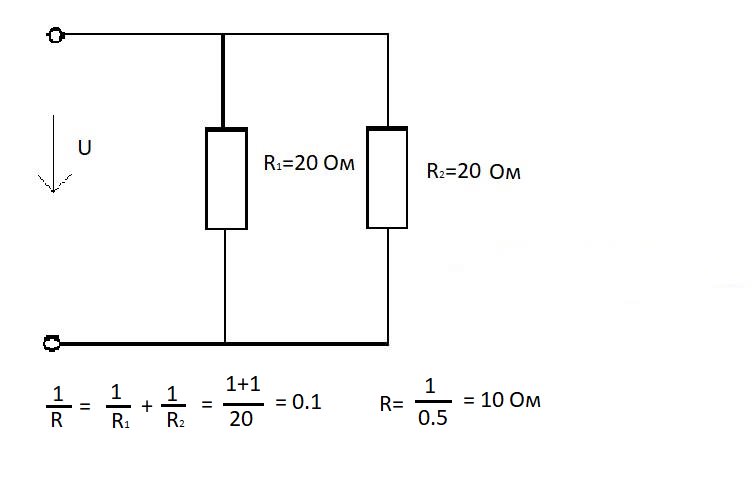 Нужно обязательно стабилизировать или хотя бы ограничить ток протекающий через светодиод. Сложные импульсные стабилизаторы тока, с высоким КПД оставим напоследок, для начала пойдем по самому простому пути: используем единственный токоограничивающий резистор и сделаем расчет сопротивления резистора для светодиода.
Нужно обязательно стабилизировать или хотя бы ограничить ток протекающий через светодиод. Сложные импульсные стабилизаторы тока, с высоким КПД оставим напоследок, для начала пойдем по самому простому пути: используем единственный токоограничивающий резистор и сделаем расчет сопротивления резистора для светодиода.
На рабочем участке вольт-амперной характеристики светодиода, при небольшом изменении напряжения ток может меняться в несколько раз, то есть светодиод ведет себя как стабилизатор напряжения. Будем пренебрегать небольшим изменением падения напряжения на светодиоде и считать его постоянным.
Калькулятор расчета сопротивления резистора для светодиода
Сразу приведу калькулятор для тех кто не хочет углубляться в теорию.
Для расчета сопротивления резистора для светодиода нам потребуются следующие данные:
Введите все данные и получите сопротивление резистора в Омах.(Если нужно ввести дробные величины, то нужно использовать десятичную точку, а не запятую. )
)
Для питания светодиодов обычно приспосабливают источники питания на 5В или 12В. В принципе это может быть любой источник питания, главное чтобы его выходное напряжение было больше чем напряжение которое должно быть на светодиоде минимум на 10-15%, чем больше разница между напряжением БП и светодиода, тем будет лучше стабильность тока, но будет хуже КПД схемы.
Максимальный ток блока питания тоже должен быть равен или больше чем ток необходимый для светодиода. Если ток окажется меньше то светодиод не будет гореть в полную силу.
Падение тока на светодиоде — справочная величина, чем короче длинная волны испускаемого света тем выше напряжение падения. Так для светодиодов красного и зеленого свечения, величина падения 1,5 — 2,5В, для синих, ультрафиолетовых и белых 3 — 3,5В.
Ток светодиода также справочный параметр, но вместо него может указываться мощность светодиода в Ваттах. И чтобы получить ток нужно будет поделить мощность на напряжение. Например светодиод на мощность 1Вт и напряжение 3,3В должен потреблять 0,3А или 300мА тока.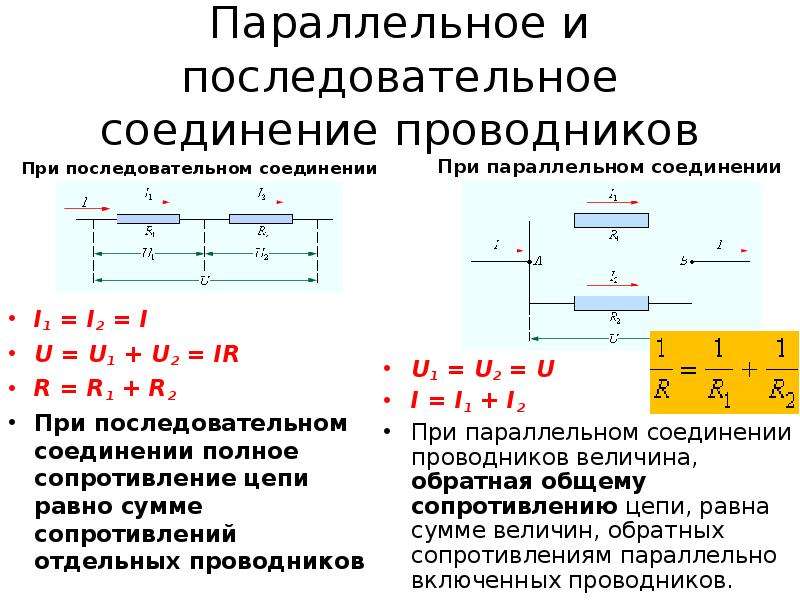
Когда все данные получены расчет резистора для светодиода не составит труда: сначала определяем падение напряжение на резисторе, для этого из напряжения питания вычитаем падение на светодиоде. А теперь по закону Ома делим это напряжение на ток, в результате и имеем сопротивление.
Если напряжения указаны в Вольтах, а токи в Амперах, то сопротивление получиться в Омах. Если использовать миллиАмперы, то сопротивление будет в килоОмах.
Пример расчета сопротивления резистора для светодиода.
Для примера возьмем уже рассматриваемый нами светодиод и подключим его к источнику питания 5В: (5В-3,3В)/0,3А=5,67Ом. Так как самый близкий из выпускаемых номиналов резисторов 5,6 Ом, то используем его.
Теперь, когда известно сопротивление резистора для светодиода, рассчитаем его мощность, для этого проще всего возвести в квадрат протекающий через резистор ток и умножить на сопротивление.
Пример расчета мощности резистора для светодиода.
Продолжаем пример: 0,3А*0,3А*5,6 Ом=0,5 Вт.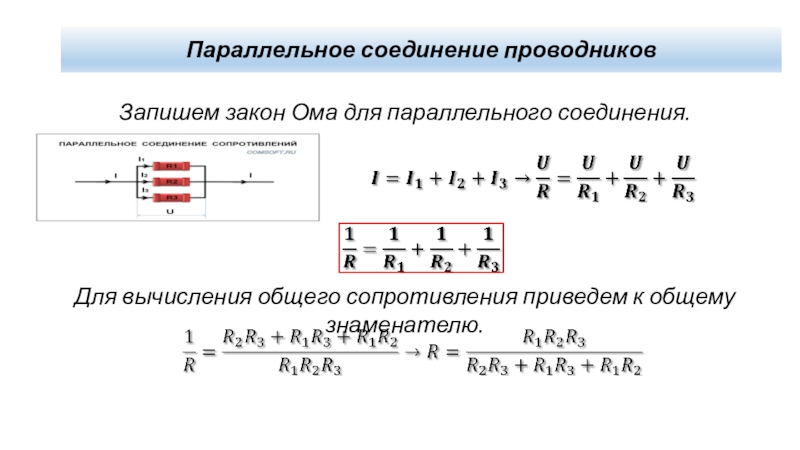
В принципе, резистор на такую мощность можно купить, также можно поставить резистор на большую мощность, но часто мощности получаются большими тогда нам поможет групповое соединение резисторов, но это тема для другой статьи.
Включение нескольких светодиодов
Часто в разных лампах или системах подсветки, требуется использовать несколько одинаковых светодиодов, так вот можно сильно сэкономить на резисторах включив последовательно несколько светодиодов и один резистор. Конечно стоимость резистора невелика, но вот то что места один резистор потребует меньше будет большим плюсом.
Для такой схемы включения сопротивление резистора рассчитывается аналогично, только вместо падения напряжения на одном светодиоде нужно подставить сумму падений напряжений на всех последовательно включенных светодиодах.
Например используя источник питания на 12В можно включить последовательно три светодиода по 3,3В ещё 2В нужно будет погасить на резисторе. Если используются светодиоды на 1Вт, то мы получим сопротивление 2В/0,3А=6,67 Ом.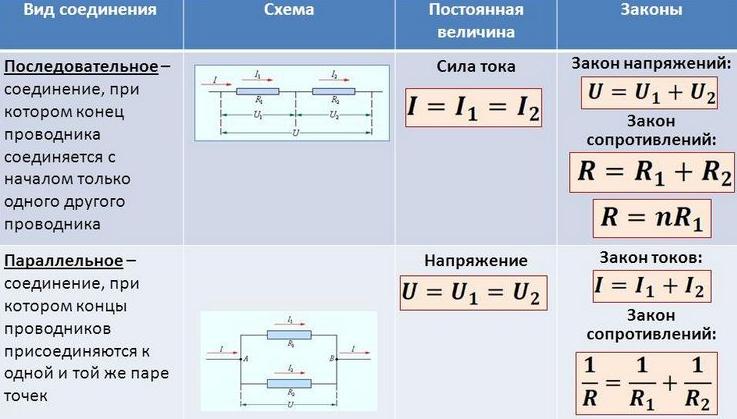 Самый близкий номинал 6,8 Ом.
Самый близкий номинал 6,8 Ом.
| Antique Electronic Supply
Используйте этот калькулятор для определения общего сопротивления сети. Этот калькулятор может давать результаты для последовательного, параллельного и любого их сочетания. Схема создается автоматически по мере добавления резисторов в сеть в качестве наглядного пособия.
Сложные резистивные схемы часто можно упростить до одного резистора эквивалентного номинала. В процессе упрощения используются два уравнения: резисторы в последовательном уравнении и резисторы в параллельном уравнении.
Резисторы серии
Резисторы включены последовательно при соединении в одну линию. Текущий ток является общим для всех резисторов в этой цепи. Это связано с тем, что ток, протекающий через первый резистор, проходит по одному пути через каждый из следующих резисторов в цепи. Общее сопротивление должно равняться сумме номиналов каждого резистора, используемого в цепи.
Мы можем рассматривать всю эту цепочку резисторов как один резистор со значением ~ R _ {\ text {Equiv}} ~.
Параллельные резисторы
Резисторы включены параллельно, если они используют одни и те же два узла. Падение напряжения на каждом резисторе в этой конфигурации обычное. Теперь ток имеет несколько путей и может не быть одинаковым для каждого резистора. Общее сопротивление резисторов, включенных параллельно, является суммой, обратной величине каждого используемого резистора.
$$ \ frac {1} {R _ {\ text {Equiv}}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ ldots \ frac { 1} {R_n} $$Мы можем рассматривать эти параллельные резисторы как один резистор со значением ~ R _ {\ text {Equiv}} ~
Обратите внимание, что информация, представленная в этой статье, предназначена только для справки.Antique Electronic Supply не делает никаких заявлений, обещаний или гарантий относительно точности, полноты или адекватности содержания этой статьи и прямо отказывается от ответственности за ошибки или упущения со стороны автора. В отношении содержания этой статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, титула, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.
В отношении содержания этой статьи не дается никаких гарантий, подразумеваемых, выраженных или установленных законом, включая, помимо прочего, гарантии ненарушения прав третьих лиц, титула, товарной пригодности или пригодности для определенной цели. или его ссылки на другие ресурсы.
Вычислитель комбинации резисторов
Эта страница не работает с отключенным JavaScript
Введите необходимое сопротивление резистора в Ом (извините, сейчас нет синтаксического анализа / преобразования единиц измерения),
выберите максимальное количество резисторов в комбинации,
выберите номиналы резисторов, доступные для создания комбинации
(вы даже можете выбрать собственные подмножества E12 или E24),
отрегулируйте тип комбинации (только параллельный, только последовательный или оба),
нажмите кнопку «Вычислить».
Имейте в виду, близость значения комбинации к требуемой
не гарантирует, что вы действительно получите это значение, используя
резисторы с допуском ± 10% (E12) или ± 5% (E24).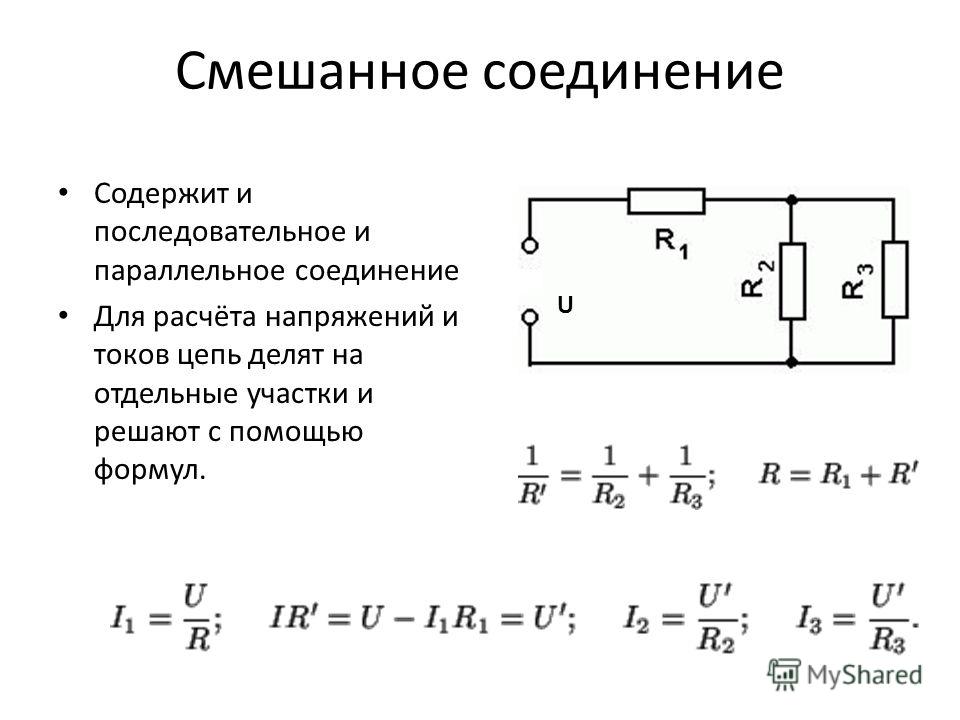
Каждый дополнительный резистор в комбинации улучшит качество полученных значений примерно на два порядка. Однако запрашиваются комбинации из большего количества резисторов. вызовет более длительный поиск комбинаций (экспоненциальный рост). Калькулятор ограничит максимальное количество резисторов в комбинации. в зависимости от количества доступных значений входного резистора.
Желаемое значение
Комплект резисторов
Пользовательское подмножество E12E24E12 Пользовательское подмножество E24
Макс. # В комбинации
123456
Комбинированный тип
Последовательный и параллельный только параллельный Только серия
Compute
- Для наборов входов до 24 значений вы можете запросить комбинации до 6 резисторов.
- Для наборов входов до 36 значений максимальное количество резисторов в комбинации составляет 5
- Для 72 входных значений (включая полный E12) могут быть запрошены комбинации до 4 резисторов
- Для более чем 72 значений будут рассматриваться только комбинации из 3 резисторов
| Комбинация (*: параллельно, +: последовательно) | Значение | отн.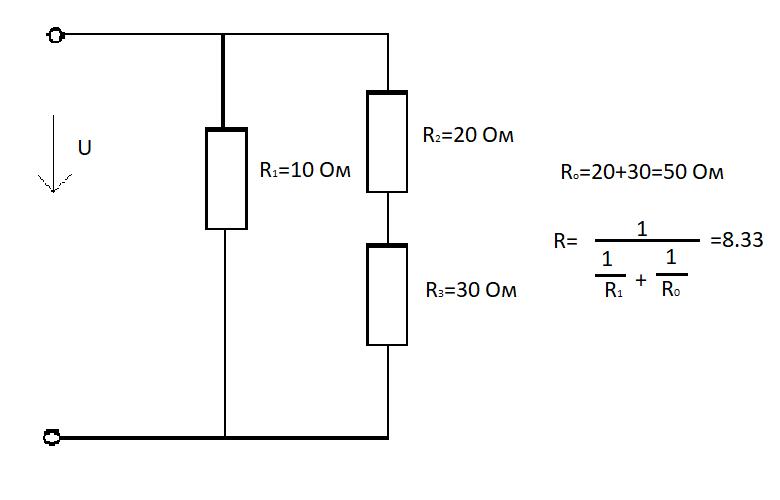 err err (% от целевого) | Мин. Значение (% от целевого) | Максимальное значение (% от целевого) |
|---|
Код
доступен на github под CC-BY- NC — это творческое сообщество, общий доступ, атрибуция, некоммерческий характер.
Пока вы используете калькулятор на этой странице, ничего страшного.
Если вы берете код и используете его для внутреннего пользования (не публикуя в Интернете), это тоже нормально.
Если вы возьмете код с github и используете его на веб-сайте без коммерческих целей, это тоже нормально.
Если вы берете код из github и используете его на веб-сайте, который вы зарабатываете на информации, опубликованной на сайте (даже если за счет рекламы), это нарушение лицензии
— Калькулятор сопротивления
Калькулятор параллельных резисторов поможет вам выбрать правильное значение сопротивления для вашей схемы.
Таблицу Excel также можно загрузить, нажав на символ ниже, который можно использовать в любое время, сохранив его на своем ноутбуке или мобильном телефоне.
Ниже приведены подробные сведения о резисторе, работе резистора, резисторах, включенных последовательно, и резисторах, включенных параллельно. Резистор Резистор — это пассивный компонент. Работа резистора заключается в том, чтобы противодействовать движению тока через него.
| Резистор |
Резистор также регулирует сигнальные каскады, разделяя напряжение в цепи делителя напряжения, смещая такие компоненты, как транзисторы, резистивные нагрузки для схем и т. Д. Символ резистора На рисунке ниже показаны символы обоих резисторов фиксированного типа.

| Обозначение резистора |
Резистор рабочий Ниже представлены детали работы резистора;
Резистор противодействует току, потому что протекающие электроны сталкиваются с атомами в резисторе и заставляют их вибрировать.
В результате электрическая энергия меняется на тепловую.Сопротивление «R» — это величина, с которой резистор противодействует потоку заряда.
Резистор работает по закону Ома Как мы знаем, закон Ома; V = I / R. Это означает, что основной принцип работы резистора или, другими словами, поведение резистора основано на законе Ома.Поясним это; согласно закону Ома напряжение (V), проходящее через резистор, пропорционально току (I), где константа пропорциональности — это сопротивление (R) i.е. электрическое сопротивление проводника постоянно.
Можно сказать, что с добавлением дополнительного напряжения, приложенного к резистору, дополнительный ток течет через него.
Поясним это на примере; Если резистор 200 Ом подключен к положительной и отрицательной клеммам источника питания 12 В постоянного тока, то через этот резистор будет протекать ток 12/200 = 0,06 А.
Параллельный и последовательный резисторы Соединяя резисторы последовательно или параллельно, мы можем очень хорошо контролировать ток.Давайте посмотрим на это подробно;Последовательные резисторы
Резисторы «Последовательно» означает, что резисторы соединены вместе или организованы гирляндой, то есть в одну линию. Полный ток, проходящий через первый резистор, должен также проходить через второй резистор, затем он проходит через третий и так далее, потому что другого пути для протекания тока нет.
Схема, показанная ниже, показывает, что резисторы R1, R2, R3 и R4 все подключены последовательно, между точкой A и точкой B, и через все они проходит общий ток (I);
| Резисторы в серии |
Следовательно, полный ток, который проходит через все эти резисторы последовательно, будет одинаковым или одинаковым в любой момент.
IR4 = IR3 = IR2 = IR1 = Itotal
Следовательно, общее сопротивление здесь складывается из всех отдельных сопротивлений резисторов, соединенных последовательно.
R1 + R2 + R3 + R4 = Rtotal = 100 Ом + 200 Ом + 300 Ом + 400 Ом = 1 кОм
Итак, в конечном итоге полное напряжение на каждом резисторе не будет одинаковым и может быть рассчитано по закону Ома. Таким образом, полное напряжение на резисторах равно сумме разностей потенциалов на каждом резисторе.
Vtotal = VAB = VR1 + VR2 + VR3 + VR4 = 1V + 2V + 3V + 4V = 10V
Резисторы, подключенные параллельно
Резисторы в «параллельном» состоянии, что оба вывода резистора или резисторы являются независимыми или индивидуально подключены к каждой клемме другого резистора или резисторов.
Схема, показанная ниже, показывает, что резисторы R1, R2, R3 и R4 подключены параллельно, между точкой A и точкой B, и через них проходит необычный ток (I);
| Параллельные резисторы |
Следовательно, здесь в любой ветви ток, проходящий через резисторы, будет неодинаковым.

I1 + I2 + I3 + I4 = Итого.
Если Vin = 10 В, то;
Itotal = 0,1 A + 0,05 A + 0,03 A + 0.025 = 0.205A
Здесь сложение обратного (1 / R) значения отдельных сопротивлений дает общее сопротивление. Можно сказать, что величина, обратная равному сопротивлению двух или более резисторов, соединенных или соединенных параллельно, является сложением инверсий каждого отдельного сопротивления.
(1 / R1) + (1 / R2) + (1 / R3) + (1 / R4) = 1 / Rtotal
= (1/100 Ом) + (1/200 Ом) + (1/300 Ом) + (1/400 Ом)
= 0,01 + 0,005 + 0,003 + 0,0025
= 0,0205 Ом
Rtotal = 1/0.0205 = 48,78 Ом
Следовательно, здесь напряжение на каждом резисторе будет одинаковым, то есть падение напряжения на всех резисторах в параллельной резистивной цепи будет одинаковым.
Vin = VR1 = VR2 = VR3 = VR4 = 10V
Параллельное соединение резистора имеет одинаковое напряжение, сопротивления могут быть разными, и, таким образом, ток, проходящий через каждый резистор, будет отличаться в соответствии с законом Ома.

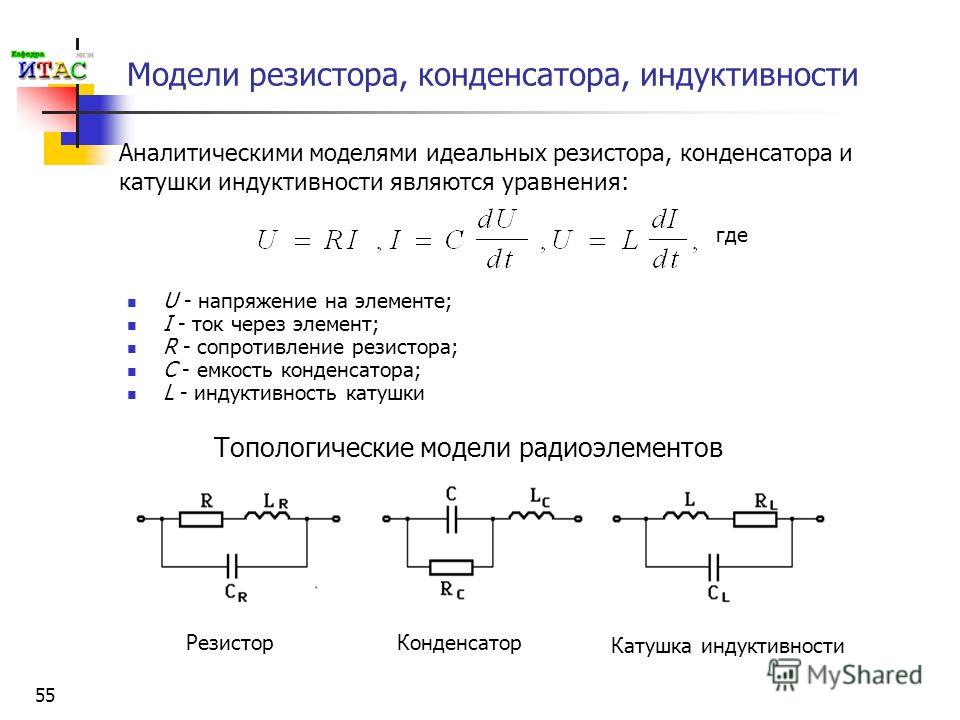 8 до 4 В.
8 до 4 В.