Расчёт пассивных RC фильтров. Онлайн калькулятор.

А не фильтрануть ли нам широким махом входной сигнал на предмет подавления помехи относительно единичного уровня на требуемой частоте, в заданное число раз отличающейся от границы полосы пропускания?
А как насчёт расчёта активных полиномиальных фильтров второго порядка на звеньях Рауха, Сален-Ки и биквадратного звена?
А кривую изменения реактивного сопротивления ёмкости в зависимости от частоты — не изобразить ли?

«Хватит умничать, пальцем покажи!», — предвижу я законное роптание посетителя, впавшего в соблазн от заголовка страницы.

И действительно. Здесь мне не тут! Базар надо фильтровать, а не безобразия нарушать!

Итак, приступим.
Для начала мы рассмотрим активные и пассивные ФНЧ, ФВЧ, ПФ без использования катушек индуктивности.

Определимся с терминологией.

— Фильтр нижних частот (ФНЧ) представляет собой устройство, которое пропускает сигналы низких частот и задерживает сигналы высоких частот.

— Фильтр верхних частот (ФВЧ) соответственно пропускает сигналы высоких частот и задерживает сигналы низких.
— Полосовой фильтр (ПФ) пропускает сигналы в некоторой полосе частот и подавляет сигналы и на низких частотах, и на высоких.
— Полоса пропускания определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности (обычно — 3дБ).
— Частотой среза фильтра называют частоту, ослабление сигнала на которой достигает -3дБ по логарифмической шкале, или 1/√2 ≈ 0.71 по линейной.
— Неравномерность АЧХ в полосе пропускания — размер флуктуации АЧХ от пика до пика в полосе пропускания.
— Крутизна частотной характеристики фильтра – скорость спада АЧХ в полосе подавления (дБ/октаву или дБ/декаду).

А начнём мы с простейших RC фильтров первого порядка. Слева фильтр нижних частот (ФНЧ), справа фильтр верхних частот (ФВЧ).

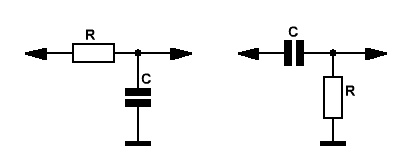
Рис.1

Крутизна спада АЧХ таких фильтров в полосе подавления — 6 дБ/октаву.
Частота среза рассчитывается по формуле: &nbsp

Теперь надо определиться — из каких соображений выбирать номиналы R и С.
Ёмкость посчитается нашей табличкой, а к выбору сопротивления резистора, для достижения заявленной крутизны, надо подойти со всей ответственностью. Номинал этого резистора должен быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления последующего.

РИСУЕМ ТАБЛИЧКУ ДЛЯ ФИЛЬТРОВ ПЕРВОГО ПОРЯДКА

ТЕПЕРЬ ТО ЖЕ САМОЕ С ДРУГИМИ ВВОДНЫМИ

Для получения простейшего полосового фильтра первого порядка, нужно последовательно соединить ФНЧ и ФВЧ с Рис.1, не забывая, что значение сопротивления R второго фильтра должно быть на порядок (в 10 раз) выше сопротивления первого.

Важно понимать, что хорошей крутизны спада АЧХ от таких простейших фильтров добиться не удастся. Тут нам прямая дорога к активным фильтрам, или к фильтрам на LC цепях.

Именно активные фильтры мы и рассмотрим на следующей странице.

 

Пассивные фильтры между ГУ и усилителем.

Плюсы и минусы, давайте пообсуждаем?

Наибольший интерес для качественного формирования необходимой АЧХ представляют пассивные RC фильтры. Это и отсутствие дополнительных шумов, всякого рода «выбросов» и «провалов», а также полное отсутствие нелинейных искажений.

Одно отсутствие индуктивности L — самого «гнусного» реактивного элемента чего стоит!
Единственным недостатком у пассивных фильтров является значительное затухание в полосе пропускания. Но так как уровень сигнала современных ГУ достаточно высок, то этим недостатком можно пренебречь. Фильтр Нижних Частот (ФНЧ) формирует АЧХ следующим образом: пропускает все частоты, начиная с нуля и «обрезая» высокие частоты (ВЧ) на частоте среза. Саму частоту среза легко можно рассчитать по формуле 1 / 2*pi*R*C, где частота в герцах, pi=3.14, сопротивление в Омах, емкость в фарадах. Крутизна среза (спада) фильтра зависит от его «порядка».
Для ФНЧ 1-го порядка она будет равна 6 дБ на октаву.
Для фильтра 2-го порядка крутизна спада АЧХ будет уже 12 дБ/окт.
Для фильтра 3-го порядка 18 дб/окт соответственно.
Чем выше порядок фильтра, тем больше затухание в полосе пропускания. Для фильтра 2-го порядка оно уже будет 20Дб, т.е. сигнал ослабляется в 10 раз. Но так как чувствительность усилителей для с обычно лежит в пределах 0,2 -2 В, а сигнал, снимаемый с ГУ, порядка 2-5 В, то получается идеальное согласование по уровням сигнала. Для качественного формирования АЧХ вполне достаточно фильтра 2-го порядка. На всех графиках, для оценки затухания на средних частотах 1000 Гц, дана контрольная точка «А». С достаточной точностью частоты раздела фильтра можно изменить, взяв за основу приведенные выше примеры. Например, чтобы снизить частоту со 100 Герц до 50 Герц, достаточно пропорционально увеличить емкость конденсатора (ов) от 22 нанофарад до 47 нанофарад. Можно также увеличить в 2 раза номиналы резисторов, но не следует забывать, что вход усилителя в этом случае должен быть высокоомный. В противном случае будет дополнительное затухание сигнала в полосе прозрачности.
Всё вышесказанное относится и к ФВЧ, на схеме меняются местами резисторы с конденсаторами.

---

Полезные темы:

Фильтр (электроника) — Википедия

У этого термина существуют и другие значения, см. Фильтр.

Фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.

Фильтры, находящие применение в обработке сигналов, бывают

Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры (по виду передаточной функции):

По порядку (степени уравнения) передаточной функции (см. также ЛАФЧХ) различают фильтры первого, второго и более высоких порядков^[1]. Крутизна ЛАЧХ фильтра 1-го порядка в полосе подавления равна 20 дБ на декаду, фильтра 2-го порядка — 40 дБ на декаду, и т. д.

По тому, какие частоты фильтром пропускаются (задерживаются), фильтры подразделяются на

Принцип работы пассивных аналоговых фильтров[править | править код]

В конструкциях пассивных аналоговых фильтров используют сосредоточенные

или распределённые реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами. Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.

Фильтры на сосредоточенных элементах[править | править код]

В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь. Однако они имеют невысокую крутизну АЧХ в полосе подавления, недостаточную во многих случаях: всего 6 дБ на октаву (или 20 дБ на декаду) — для RC-фильтра, являющегося фильтром 1-го порядка и 40 дБ/декада для LC-фильтра, являющегося фильтром 2-го порядка. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.

RС-фильтр нижних частот 1-го порядка[править | править код]

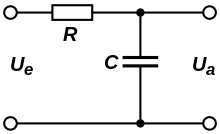Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора R{\displaystyle R} и конденсатора C{\displaystyle C}, образующего делитель напряжения входного сигнала. Комплексный коэффициент передачи KRC{\displaystyle K_{RC}} такого делителя:

KRC=UaUe=ZCR+ZC=1/jωCR+1/jωC=1T2ω2+1−j⋅TωT2ω2+1,{\displaystyle K_{RC}={\frac {U_{a}}{U_{e}}}={\frac {Z_{C}}{R+Z_{C}}}={\frac {1/j\omega C}{R+1/j\omega C}}={\frac {1}{T^{2}\omega ^{2}+1}}-j\cdot {\frac {T\omega }{T^{2}\omega ^{2}+1}},}

где T=RC{\displaystyle T=RC} — постоянная времени RС-цепи.

Модуль коэффициента передачи этой цепи:

|KRC|=1ω2/ω02+1,{\displaystyle |K_{RC}|={\sqrt {\frac {1}{\omega ^{2}/\omega _{0}^{2}+1}}},}

где ω0=1/T.{\displaystyle \omega _{0}=1/T.}

При входной частоте ω≪ω0{\displaystyle \omega \ll \omega _{0}} модуль коэффициента передачи близок к 1, при ω≫ω0{\displaystyle \omega \gg \omega _{0}} модуль коэффициента передачи близок к 0, на частоте ω=ω0{\displaystyle \omega =\omega _{0}} модуль коэффициента передачи равен |KRC|=1/2{\displaystyle |K_{RC}|=1/{\sqrt {2}}} — уменьшение относительно единичного коэффициента передачи приблизительно на 3,01 дБ, эта частота называется частотой среза фильтра. В полосе подавления при частоте много выше частоты среза модуль коэффициента передачи уменьшается на 20 дБ на декаду изменения частоты.

LС-фильтр нижних частот 2-го порядка[править | править код]

Простейший пассивный LC-фильтр нижних частот 2-го порядка

На рисунке показан пример простейшего LC-фильтра нижних частот 2-го порядка: при подаче гармонического сигнала определённой частоты на вход фильтра (на рисунке слева) напряжение на выходе фильтра (справа) в установившемся режиме определяется отношением реактивных сопротивлений катушки индуктивности (XL=ωL{\displaystyle X_{L}=\omega L}) и конденсатора (XC=1/ωC{\displaystyle X_{C}=1/\omega C}).

Коэффициент передачи ФНЧ можно вычислить, рассматривая этот фильтр как делитель напряжения, образованный реактивными сопротивлениями.

Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть ZL=jωL=jXL{\displaystyle Z_{L}=j\omega L=jX_{L}} и комплексное сопротивление конденсатора ZC=1/(jωC)=−jXC{\displaystyle Z_{C}=1/(j\omega C)=-jX_{C}}, где j2=−1{\displaystyle {j}^{2}=-1} — мнимая единица, ω{\displaystyle \omega } — угловая частота входного гармонического сигнала, поэтому для ненагруженного LC-фильтра коэффициент передачи K{\displaystyle K} будет выражаться формулой для делителя напряжения:

K=ZCZL+ZC{\displaystyle K={\frac {Z_{C}}{Z_{L}+Z_{C}}}}.

Подставляя в формулу выражения для комплексных сопротивлений, получим для частотно-зависимого коэффициента передачи:

K(ω)=11−ω2LC=11−(ω/ω0)2{\displaystyle K(\omega )={\frac {1}{1-\omega ^{2}\,LC}}={\frac {1}{1-(\omega /\omega _{0})^{2}}}}.

Как видно, коэффициент передачи ненагруженного идеального ФНЧ источником сигнала для которого является идеальный генератор напряжения с нулевым внутренним сопротивлением неограниченно растет с приближением к резонансной частоте ω0=1/LC{\displaystyle \omega _{0}=1/{\sqrt {LC}}}, так как знаменатель выражения стремится к нулю. При повышении частоты выше резонансной — убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю.

Принято называть зависимость модуля комплексного коэффициента передачи фильтра от частоты амлитудно-частотной характеристикой (АЧХ), а зависимость фазы от частоты — фазо-частотной характеристикой (ФЧХ).

В реальных схемах к выходу фильтра подключается активная нагрузка^[2], которая понижает добротность фильтра и устраняет острый всплеск коэффициента передачи вблизи частоты резонанса ω0{\displaystyle \omega _{0}}.

Величину ρ=L/C{\displaystyle \rho ={\sqrt {L/C}}} называют характеристическим сопротивлением фильтра или волновым сопротивлением фильтра. Если ФНЧ нагрузить на активное сопротивление, равное характеристическому, то передаточная функция станет нерезонансной, коэффициент передачи будет примерно постоянный для частот ω<ω0{\displaystyle \omega <\omega _{0}}, и убывающий как 1/ω2{\displaystyle 1/\omega ^{2}} на частотах выше ω0{\displaystyle \omega _{0}}. На частоте ω0{\displaystyle \omega _{0}} коэффициент передачи такого ФНЧ уменьшается на 3 дБ относительно значения коэффициента передачи на низкой частоте, эту частоту называют частотой среза фильтра. На частотах много выше частоты среза коэффициент передачи уменьшается на 40 дБ на декаду изменения частоты.

Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается выражение для коэффициента передачи:

K(ω)=(ω/ω0)21−(ω/ω0)2{\displaystyle K(\omega )={\frac {(\omega /\omega _{0})^{2}}{1-(\omega /\omega _{0})^{2}}}}.

На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.

Фильтры с распределёнными параметрами (фильтры СВЧ)[править | править код]

На сверхвысоких частотах сосредоточенные элементы (конденсаторы и катушки индуктивности) практически не используются, так как с ростом частоты их типичные для этого диапазона номиналы, а следовательно и габариты, уменьшаются настолько, что изготовление их становится невозможным. Поэтому применяются так называемые линии с распределёнными параметрами, в которых индуктивность, ёмкость и активная нагрузка равномерно или неравномерно распределены по всей линии. Так, элементарный ФНЧ, рассматриваемый в предыдущем разделе, состоит из двух сосредоточенных элементов, представляющих собой резонатор; в случае же распределённых параметров фильтр будет состоять из одного элемента-резонатора (например отрезка микрополосковой линии или металлического стержня).

Конструкции СВЧ фильтров весьма разнообразны, и выбор конкретной реализации зависит от предъявляемых к устройству требований (значение рабочих частот, добротность, максимальное затухание в полосе задержания, расположение паразитных полос пропускания).

Проектирование фильтров на распределённых параметрах является достаточно сложным процессом, состоящим из двух этапов: получение электрических параметров, исходя из требований к устройству; получение габаритных параметров из полученных электрических. В основе современных методов проектирования микроволновых фильтров лежит теория связанных резонаторов.

Электромеханические фильтры[править | править код]

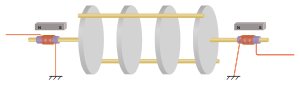ЭМФ с дисковыми изгибными резонаторами и магнитрострикционными преобразователями

Электромеханический фильтр (ЭМФ) содержит механическую резонансную систему (резонатор) той или иной конструкции. На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего тела фильтра и обратно.

ЭМФ получили распространение в трактах промежуточной частоты высококачественных радиосистем (в том числе военных, морских, радиолюбительских и других). Их преимуществом является значительно бо́льшая, чем у эквивалентных LC-фильтров, добротность, позволяющая достичь высокой избирательности, необходимой для разделения близких по частоте радиосигналов в приёмниках.

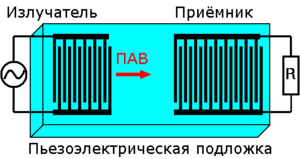
Фильтры на поверхностных акустических волнах (ПАВ)[править | править код]

Принцип работы активных аналоговых фильтров[править | править код]

Активные аналоговые фильтры строятся на основе усилителей, охваченных петлёй обратной связи (положительной или отрицательной). В активных фильтрах возможно избежать применения катушек индуктивности, что позволяет уменьшить физические размеры устройств, упростить и удешевить их изготовление.

LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприёмника обеспечивает настройку на определённую радиостанцию.

Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ, для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.

1. ↑ Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него реактивных элементов.
2. ↑ А также всегда присутствует активное сопротивление катушки индуктивности и ненулевое выходное сопротивление источника сигнала, что тоже понижает добротность фильтра.
3. ↑ Например, фильтры на поверхностных акустических волнах для электроники цветных стационарных телевизионных приёмников.

• Р. Богнер, А. Константинидис. Введение в цифровую фильтрацию. — Москва: Мир, 1976.
• Э. Оппенгейм. Применение цифровой обработки сигналов. — Москва: Мир, 1980.

Активные и пассивные электрические фильтры

Библиографическое описание:

Магеррамов Р. В. Активные и пассивные электрические фильтры // Молодой ученый. — 2017. — №2. — С. 148-152. — URL https://moluch.ru/archive/136/38046/ (дата обращения: 05.02.2020).



Фильтр — устройство, которое передает сигналы в определенной области частот и препятствует прохождению сигналов вне этой области. Идеальный фильтр имеет постоянную и отличную от нуля передаточную характеристику в необходимом диапазоне частот (полоса пропускания или прозрачности) и нулевую в остальном диапазоне (полоса подавления или затухания).

Применение фильтров имеет очень большую потребность в радио и телеаппаратуре, в которой осуществляется настройка каналов на определённой частоте с помощью фильтрования принимаемых сигналов. Помимо радиотехники, фильтры применяются в аналого-цифровом и цифро-аналоговом преобразовании сигналов, а также в различных электронных системах, с целью фильтрации помех.

Одна из классификаций электрических фильтров — классификация по типам элементов, используемых для схемотехнической реализации: активные, пассивные фильтры, LC, RC-фильтры, фильтры на переключаемых конденсаторах и т. д. Пассивные фильтры (Рисунок 1) имеют в своем составе только пассивные элементы такие, как резисторы, индуктивности, конденсаторы. Данный тип фильтров не требует источника питания для функционирования и не усиливает мощность выходного сигнала (в отличие от активного фильтра). В активном фильтре (Рисунок 2) используется один или несколько активных компонентов: транзистор или операционный усилитель.

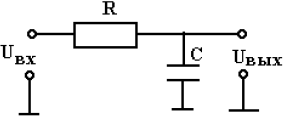
Рис. 1. Схема пассивного фильтра нижних частот

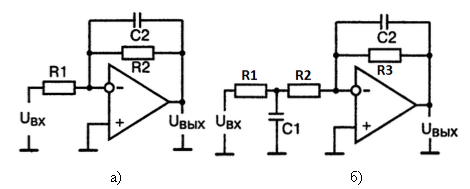
Рис. 2. Схемы активного фильтра нижних частот на операционном усилителе: а) первого б) второгопорядка

Порядок фильтра определяет максимальное количество нулей и полюсов передаточной функции фильтра. Что бы увеличить крутизну амплитудно-частотной характеристики необходимо увеличить порядок фильтра, но стоит отметить, что при увеличении порядка увеличивается и количество реактивных элементов (конденсаторов, резисторов) что в свою очередь усложняет сам фильтр и увеличивает его чувствительность к разбросу параметров его компонентов.

В идеальном случае разработчику хотелось бы получить амплитудно-частотную характеристику (АЧХ) имеющую резкий переход между полосой пропускания и подавления (Рисунок 3). Применяя пассивные элементы фильтрации, увеличение крутизны перехода характеристики АЧХ добиваются применением фильтров более высокого порядка, данных подход требует больших расчетов и более точной настройки. Однако применение активных фильтров основным элементом, которых является операционный усилитель с обратной связью, позволяет получить крутой спад характеристики АЧХ, затрачивая значительно меньше усилий и средств во время разработки и при изготовлении.

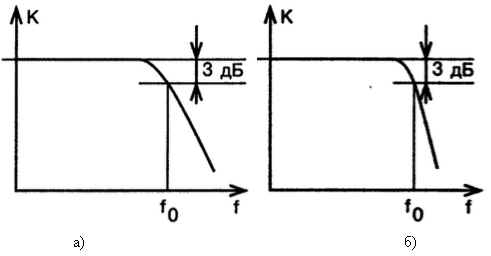
Рис. 3. АЧХ фильтра нижних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду

Помимо классификации фильтров по типам элементов, на которых они построены, фильтры классифицируются и по виду амплитудно-частотной характеристики:

– Фильтр высоких частот (ФВЧ) — подавляет амплитуды гармонического сигнала ниже частоты среза (Рисунок 4).

– Фильтр низких частот (ФНЧ) — подавляет амплитуды гармонического сигнала выше частоты среза (Рисунок 2).

– Полосовой фильтр — подавляет амплитуды гармонического сигнала выше и ниже определенной полосы (Рисунок 6).

– Полосно-заграждающий фильтр — подавляет амплитуды гармонического сигнала в определенном диапазоне частот, т. е. фильтр, подавляющий колебания определенной полосы и пропускающий колебания, выходящие за границы этой полосы.

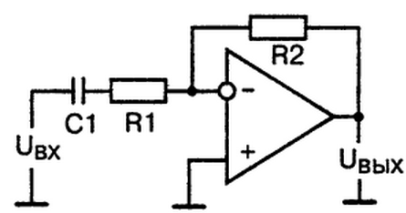
Рис. 4. Схема активного фильтра верхних частот первого порядка

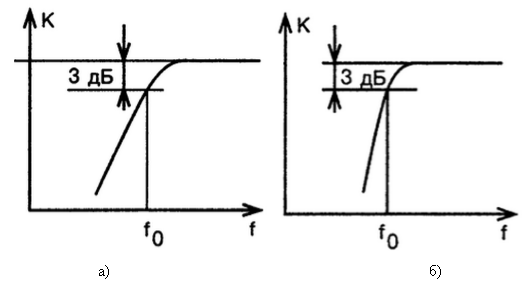
Рис. 5. АЧХ фильтра верхних частот а) первого порядка, спад 20 dB на декаду; б) второго порядка, спад 40 dB на декаду

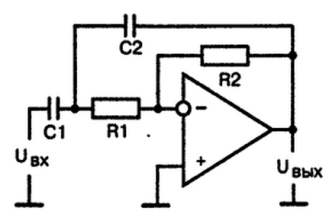
Рис. 6. Схема активного полосового фильтра

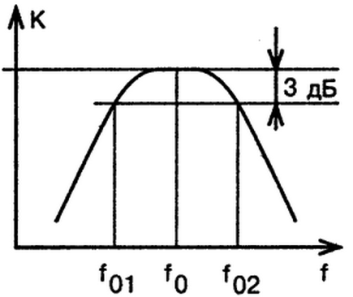
Рис. 7. АЧХ активного полосового фильтра

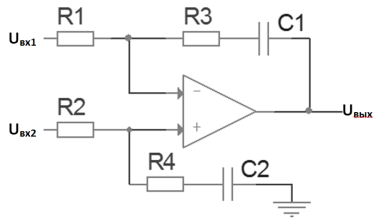
Рис. 8. Пропорционально-интегрирующий фильтр низких частот

Пропорционально-Интегриующий фильтра на ОУ (ПИ-фильтр), также является активным фильтром. ПИ-фильтр сравнивает средние значения двух входных сигналов за период частоты, резисторы R1 и R2 определяют масштабный коэффициент сравнения. Произведение C1*R1 (постоянная времени интегратора Ти) определяет интегрирующий эффект фильтра, резистор R3 обеспечивает устойчивость схемы ФАПЧ, а отношение R3 к R1 определяет пропорциональный коэффициент фильтра Кп.

Заключение

Фильтрация сигналов является важной функцией в аналоговых и аналого-цифровых устройствах, в зависимости от поставленных задач используется тот или иной тип схемотехнической реализации фильтра. В данной статье были рассмотрены несколько разновидностей электрических фильтров и их амплитудно-частотная характеристика. Широкое применение фильтров встречается в электротехнике, радиотехнике и электронике.

Активные фильтры часто применяются в геофизических, медицинских устройствах, а также в различных устройствах связи. Обычно фильтр такого типа представляет собой соединение цепей второго-первого порядка. Благодаря этому упрощается расчет и настройка данного фильтра.

Литература:

1. Изюмов Н. М. — Радиорелейная связь, Рипол Классик, 2013
2. Кеоун Д. — OrCAD Pspice. Анализ электрических цепей, Litres, 2014
3. Мелешин В. — Транзисторная преобразовательная техника, Litres, 2016
4. Тимошенков В. П., А. А. Миндеева — Элементная база систем связи, учебное пособие, 2015
5. Миндеева А. А. — Элементная база аналоговых схем, учебное пособие, 2012
6. У.Титце, К.Шенк — Полупроводниковая схемотехника, 2010 г.
7. M. Williamsen, «Notch-Filter Design», Audio Electronics, Jan. 2000
8. W. Jung, «Bootstrapped IC Substrate Lowers Distortion in JFET Op Amps», Analog Devices AN232
9. H. Zumbahlen, «Passive and Active Filtering», Analog Devices AN281
10. P. Toomey & W. Hunt, «AD7528 Dual 8-Bit CMOS DAC», Analog Devices AN318
11. http://www.dsplib.ru/content/filters/ch3/ch3.html
12. http://radio-hobby.org/modules/news/article.php?storyid=1162

Основные термины (генерируются автоматически): фильтр, активный фильтр, амплитудно-частотная характеристика, гармонический сигнал, частота, операционный усилитель, активный полосовой фильтр, полоса пропускания, порядок фильтра, тип элементов.

Пассивные и активные режекторные фильтры. Онлайн расчёт.

Режекторный фильтр — не частый гость в наших краях. Зверь редкий, нелюдимый, но для радиолюбительского хозяйства — весьма полезный. Внешне напоминает полосовых собратьев, но охотится исключительно за сигналами вокруг центральной частоты и мало активен на частотах, выходящих за пределы отведённого ему диапазона.

Для начала определимся с терминологией.

Полосно-заграждающий фильтр (он же — режекторный фильтр, он же — фильтр-пробка) — электронный или любой другой фильтр, не пропускающий сигналы со входа на выход в определённой полосе частот, но имеющий близкий к единице коэффициент передачи при более низких и более высоких частотах.
Эта полоса подавления характеризуется шириной полосы заграждения и расположена вокруг центральной частоты подавления fо.
Заграждающий фильтр, предназначенный для подавления одной определённой частоты, называется узкополосным заграждающим фильтром или фильтром-пробкой.

Для описания режекторных фильтров используют следующие параметры:
центральная частота подавления fо;
две граничных частоты – нижняя fн и верхняя fв, при которых Кu = 0,7mах;
диапазон частот Δf = fв − fн, называемый полосой задержания;
параметр Q = (fв + fн)/(2Δf), называемый добротностью.

Простейшие Т-образные фильтры и их амплитудно-частотная характеристика приведены на Рис.1.

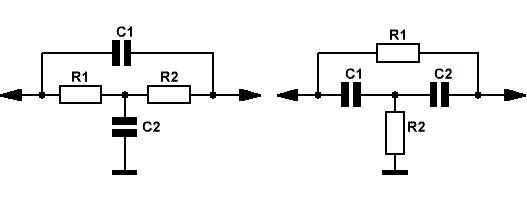
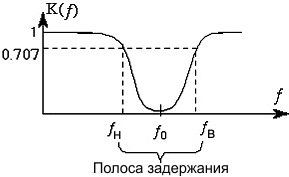
Рис.1

Центральная частота подавления этих фильтров рассчитывается по формуле: fо = 1/(2π*R*C) при R1=R2=R, C1=C2=C. Глубина режекции — всего 10 дБ, а полоса задержания составляет значение, в 5-6 раз превышающее fо.

Именно в силу указанных выше хилых характеристик — подобные простейшие цепи уступили позиции двойным Т-образным RC-фильтрам (Рис.2), часто называемым 2ТФ.

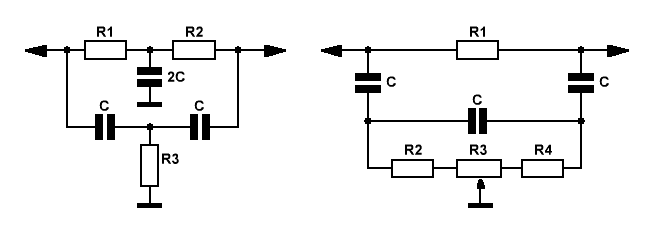
Рис.2 Рис.3

Двойной Т-образный RC-фильтр при определённых условиях (симметрия моста, точный подбор элементов, согласование входа и выхода) почти полностью подавляет центральную частоту fo. Глубина режекции (подавления частоты fo) при работе на высокоомную нагрузку достигает 50 дБ. Добротность Q — около 0,3.

На Рис.2 приведена классическая схема двойного Т-образного режекторного фильтра, на Рис.3 — с возможностью плавной регулировки центральной частоты подавления.

Начнём с нерегулируемой схемы.
Обычно выбираются следующие соотношения элементов R2=R1, R3=R1/2.
Номиналы этих резисторов должны быть на порядок больше выходного импеданса предыдущего каскада и на порядок меньше входного сопротивления последующего.
Ничего не изменилось, центральная частота вычисляется по формуле fо = 1/(2π*R*C).

РИСУЕМ ТАБЛИЦУ ДЛЯ ДВОЙНЫХ Т-ОБРАЗНЫХ RC-ФИЛЬТРОВ

При желании ввести регулировку центральной частоты подавления fо с диапазоном перекрытия по частоте более чем в 2 раза, при сохранении параметров, присущих двойным Т-образным режекторным фильтрам, имеет смысл воспользоваться схемой, приведённой на Рис.3.

Значение резистора R1 должно в 6 раз превышать суммарную величину R2, R3 и R4, поэтому его следует выбирать номиналом — не менее 100 кОм.
Формула для расчёта частоты подавления fо = 1/(2πС√3×R_{3_1}×R_{3_2}), где R_{3_1} — сумма сопротивлений слева от регулирующего вывода R3, а R_{3_2} — справа.

Рисуем таблицу и для таких фильтров.

ТАБЛИЦА ДЛЯ ПЕРЕСТРАИВАЕМЫХ РЕЖЕКТОРНЫХ RC-ФИЛЬТРОВ

Дальнейшего улучшения параметров режекторных фильтров можно добиться введением в схему на Рис.2 положительной обратной связи, подаваемой в точки, идущие к земляной шине.
В результате подобных действий фильтры становятся активными и приобретают следующий вид.

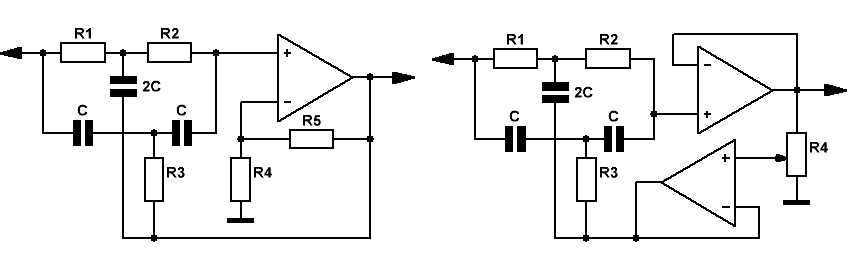
Рис.4 Рис.5

На Рис.4 приведена схема активного режекторного фильтра на основе простого двойного Т-моста.

Значение добротности определяется отношением значений резисторов K=R5/R4. При изменении этого отношения в диапазоне К=0.01-0.2 добротность Q меняется практически линейно и принимает значения от 30 до 2. Дальнейшее увеличение параметра К не приветствуется, в связи с ухудшением неравномерности АЧХ в полосе пропускания.

Для желающих же регулировать значение добротности в более широких пределах на Рис.5 приведена схема активного режекторного фильтра на двух операционных усилителях. Здесь переменный резистор R4 позволяет изменять добротность в пределах 50 — 0.3.

А при необходимости получить перестраиваемый по частоте активный режекторный фильтр, регулирующий вывод переменного резистора R3 на Рис.3, точно таким же образом подключается к выходу операционного усилителя. Результатом является схема, изображённая на Рис.6 .

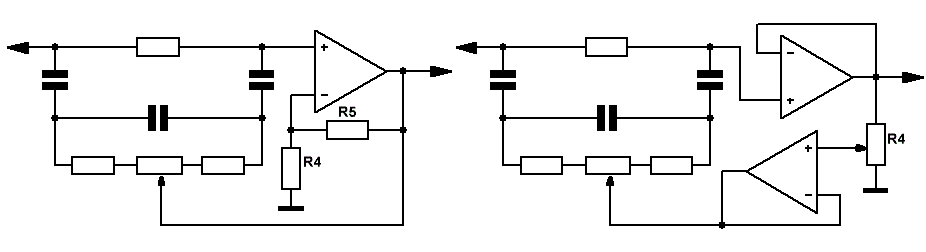
Рис.6 Рис.7

На Рис.7 приведена схема режекторного фильтра, позволяющая регулировать как частоту подавления, так и добротность в широких пределах.

Обе таблицы для расчёта частотозадающих элементов остаются в силе!

Ну, да и хватит, на следующей странице будем мурыжить режекторные LC фильтры.