зонд — это… Что такое Лямбда-зонд?

Лямбда-зонд (λ-зонд) — датчик кислорода в выпускном коллекторе двигателя. Позволяет оценивать количество оставшегося свободного кислорода в выхлопных газах.

Датчик основан на свойствах оксида циркония — ZrO₂ и начинает работать только при температурах более 350 °C. Для ускорения прогрева датчика в него монтируют электронагреватель, потому обычно датчик имеет пару сигнальных проводов и пару от подогревателя.

Рабочий элемент датчика — пористый керамический материал на основе двуокиси циркония, покрытый методом напыления платиной. Выхлопные газы обтекают рабочую поверхность. Датчик реагирует на разницу между уровнем кислорода в выхлопных газах и в атмосфере, вырабатывая на выходе соответствующую разность потенциалов. Первые «лямбда-зонды» были резистивными, то есть изменяли свое сопротивление. Современные датчики работают как пороговые элементы.

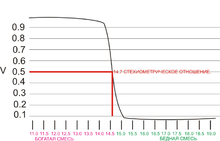
Сигнал используется системой управления для поддержания оптимального (стехиометрического, около 14,7:1) соотношения воздух/бензин в камерах сгорания. В стехиометрии — λ = (реальное к-во воздуха) / (необходимое к-во воздуха).

• λ=1 — стехиометрическая (теоретически идеальная) смесь;
• λ>1 — бедная смесь;
• λ<1 — богатая смесь (избыток бензина, воздуха не хватает для полного сгорания).

Поскольку некоторое количество кислорода должно присутствовать в выхлопе для нормального дожигания СО и СН на катализаторе, для более точного регулирования используют второй датчик, расположенный за катализатором.

Датчик на основе оксида циркония

В датчике на основе оксида циркония происходит реакция восстановления двуокиси циркония ZrO₂ до окиси циркония ZrO, инициируемая платиновым катализатором, покрывающим чувствительный элемент датчика и являющаяся причиной возникновения ЭДС. На поверхности датчика окислительные процессы чередуются с восстановительными, что обеспечивает автоматическое поддержание работоспособности λ-зонда и его высокую чувствительность к изменению концентрации окисляемых компонентов.

Для того что бы подавить реакцию окисления недоокисленных компонентов отработавших газов кислородом чувствительного элемента датчика, то есть прекратить генерацию ЭДС датчиком, необходимо присутствие в отработавших газах избыточного, по отношению к стехиометрическому, количества кислорода, причем количество избыточного кислорода растет обратно пропорционально концентрации недоокисленных компонентов отработавших газов. Используя это свойство λ-зонда, представляется возможным оценить концентрацию в отработавших газах продуктов неполного сгорания топлива и использовать эту информацию для оценки эффективности работы каталитического нейтрализатора.

Широкополосный датчик на основе оксида циркония

Разновидность датчика на основе оксида циркония.

Основная разница зонда с широкой панелью LSU 4 по отношению к обычным λ-зондам — это комбинация сенсорных ячеек и так называемых накачиваемых кислородом ячеек. Ячейки разделены диффузионным зазором шириной от 0,01 до 0,05 мм. Состав его газового содержимого постоянно соответствует λ=1, что для сенсорной ячейки значит напряжение в 450 милливольт. Поддерживается содержание газа и вместе с ним напряжение сенсора посредством различных напряжений сенсора накачиваемых элементов. При бедной смеси и напряжении сенсора ниже 450 милливольт ячейка выкачивает кислород из диффузионного отверстия. Если смесь влажная и напряжение лежит выше 450 милливольт, ток меняет свое направление, и накачивающие ячейки транспортируют кислород в диффузионные расщелины. При этом интегрированный нагревающий элемент устанавливает температуру области от 700 до 800 градусов.

При отказе датчика система переходит в аварийный режим без коррекции содержания воздуха в смеси.

Одной из основных причин отказа датчика в России являлось отравление тетраэтилсвинцом. По мере перехода на качественный неэтилированный бензин эта проблема уходит в прошлое.

Ток широкополосного датчика I_pn и соответствующие значения λ^[1]:

Ipn, мА	-5.000	-4.000	-3.000	-2.000	-1.000	-0.500	0.000	0.500	1.000	1.500	2.000	2.500	3.000	4.000
λ	0.673	0.704	0.753	0.818	0.900	0.948	1.000	1.118	1.266	1.456	1.709	2.063	2.592	5.211

Примечания

Ссылки

исчисление — это… Что такое Лямбда-исчисление?

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.

λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию. λ-исчисление реализовано Джоном Маккарти в языке Лисп. Вначале реализация идеи λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.

Чистое λ-исчисление

Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами (обами), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличия каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если  — выражение, свободно содержащее , тогда запись означает: функция от аргумента , которая имеет вид , обозначает функцию . Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы свободно входило в , не очень существенно — достаточно предположить, что , если это не так.

β-редукция

Поскольку выражение обозначает функцию, ставящую в соответствие каждому значение , то для вычисления выражения

,

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм вместо переменной . В результате получается . Это соображение в общем виде записывается как

и носит название β-редукция. Выражение вида , то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

η-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применённые к любому аргументу, дают одинаковые результаты. η-преобразование переводит друг в друга формулы и (в обратную сторону — только если не имеет свободных вхождений в : иначе свободная переменная после преобразования станет связанной внешней абстракцией).

Функция двух переменных и может быть рассмотрена как функция одной переменной , возвращающая функцию одной переменной , то есть как выражение . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется

карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D → D до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n — 1).

В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого, аргумент, ссылающийся на себя (здесь обозначен как r), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз. Так как существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))

В лямбда-исчислении, Y g — неподвижная точка g; продемонстрируем это:

Y g

λh.((λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g).

Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g) n, где n — число, для которого вычисляется факториал. Пусть n = 4, получаем:

   g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции.

См. также

Примечания

1. ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.
• Чечулин В. Л. О непротиворечивости лямбда-исчисления // В мире научных открытий, серия Математика. Механика. Информатика, 2011, № 1, сс. 203—206

Лямбда-зонд — Википедия. Что такое Лямбда-зонд

Лямбда-зонд (λ-зонд) — датчик остаточного кислорода (например, в выпускном коллекторе двигателя или дымоходе отопительного котла). Позволяет оценивать количество оставшегося не сгоревшего топлива либо кислорода в выхлопных газах. Данные показания позволяют приготовлять оптимальную воздушно-топливную смесь, а также снижать количество вредных для человека побочных продуктов процесса сгорания.

Узкополосный лямбда-зонд

Лямбда-зонд порогового типа действует по принципу гальванического элемента/твердооксидного топливного элемента с твердым электролитом в виде керамики из диоксида циркония (ZrO₂). Керамика легирована оксидом иттрия, а поверх неё напылены токопроводящие пористые электроды из платины, одновременно являющейся катализатором окислительно-восстановительных реакций. Один из электродов омывается горячими выхлопными газами (внешняя сторона датчика), а второй — воздухом из атмосферы (внутренняя сторона датчика). Эффективное измерение состава отработавших газов лямбда-зонд обеспечивает после разогрева до определенной температуры выше 300°C. Только в таких условиях циркониевый электролит приобретает проводимость, а гальваническая ячейка начинает работать. Для работы датчика атмосферный кислород нужен в очень небольшом количестве, поэтому, в целом герметичный для воды, датчик делается таким образом, чтобы кислород немного попадал внутрь со стороны проводки.

Если при работе двигателя и датчика ионы свободного кислорода присутствуют лишь с внутренней стороны элемента, то есть имеется лишь атмосферный кислород, то разогретая ячейка самостоятельно начинает генерировать ЭДС, а значит, на блок управления с датчика начинает поступать электрический ток с определённым напряжением. Это означает для ЭБУ автомобиля, что смесь была «богатой». На практике этому соответствует примерно 0,8-0,9 вольт. Если свободный кислород появляется в составе выхлопа с внешней стороны датчика, то выработка ЭДС снижается, а если кислорода достаточно много, то полностью прекращается, то есть кислород из выхлопа блокирует работу ячейки. Это означает для ЭБУ, что смесь была «бедной». На практике этому соответствует примерно 0,1-0,2 вольт. Если ЭДС стремится к нулю, то это означает что смесь абсолютно бедная, например в двигатель не поступает топливо. Напряжение с датчика 0,45 вольт считается оптимальным, и свидетельствует, что сжигаемая смесь обладает стехиометрическим соотношением топлива и воздуха.

Конструктивно, датчики делятся по числу проводов и наличию подогревательного элемента. Датчики без нагревательного элемента используют 1 или 2 провода, с нагревательным элементом — 3 или 4 провода. Первое поколение датчиков разогревалось лишь от выхлопных газов, поэтому начинало давать сигнал сравнительно поздно после старта двигателя. Появившиеся позже датчики с нагревательным элементом стали выводить датчик в рабочее состояние очень быстро, что отвечало возросшим требованиям экологии, а также позволяло использовать датчик, когда температуры выхлопных газов оказывалось недостаточно.

В начале работы, после запуска мотора, лямбда-зонд не выдаёт показаний, и ЭБУ вынужден использовать только карты впрыска, прописанные в нём. Это режим работы без обратной связи, и коррекции топливной смеси по лямбда-зонду в этом режиме нет. Когда с датчика появляется сигнал, то ЭБУ автомобиля переходит в режим работы с обратной связью, при котором исходные топливные карты корректируются с учётом показаний с лямбда-зонда в режиме реального времени.

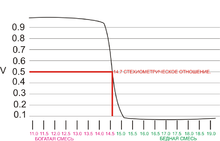
Сигнал используется системой управления для поддержания оптимального (стехиометрического, около 14,7:1) соотношения воздушно-топливной смеси.

• λ=1 — стехиометрическая (теоретически идеальная) смесь;
• λ>1 — бедная смесь;
• λ<1 — богатая смесь (избыток топлива, воздуха не хватает для полного сгорания).

Работа датчика не линейна во времени, показания отклоняются от оптимального очень быстро, поэтому ЭБУ вынужден постоянно корректировать смесь. При этом двигатель редко работает на идеальном стехиометрическом составе смеси, однако смесь постоянно стремится к достижению идеальной пропорции. Лямбда-зонд не сообщает о том, сколько именно кислорода в выхлопных газах, он сигнализирует о том, есть ли свободный кислород в выхлопе или нет. Факт наличия свободного кислорода и означает, что топлива в смеси должно быть больше, поскольку часть кислорода не вступила в реакцию. И наоборот, если кислорода нет или очень мало, то требуется уменьшить подачу топлива, тем более, что если топлива окажется слишком много, то это приведёт к появлению сажи и так называемого «грязного» выхлопа. В реальности, достичь и долго удерживать идеальную стехиометрическую смесь невозможно, так как существует множество факторов, постоянно влияющих на смесеобразование и её сгорание. Поэтому, целью является не само достижение стехиометрического соотношения, а стремление к этому, путём постоянной коррекции смеси и пребывания её поочередно то в «условно-бедном», то в «условно-богатом» состоянии, не отдаляясь от оптимального состава. Правильность работы датчика даёт возможность максимально сократить разницу между реальным соотношением воздуха/топлива и стехиометрическим.

График вольтажа с датчика обычно имеет вид синусоиды с довольно резким переходом от верхних значений к нижним, и наоборот. Принцип цикла таков: датчик сообщил, что смесь «бедная» — ЭБУ начинает постепенно добавлять топлива; далее датчик сообщает, что смесь стала «богатой» — ЭБУ начинает уменьшать подачу топлива, и так постоянно, пока активна обратная связь. Изменение подачи топлива (как реакция на показания лямбда-зонда) обычно выполняется с использованием двух переменных в ЭБУ — «долгая» коррекция и «краткая» коррекция, и они заложены в стандарт диагностики OBD-II. Краткая коррекция позволяет смеси следовать за датчиком сиюсекундно. Долгая коррекция вычисляется ЭБУ на основании анализа краткой коррекции, и нужна для того чтобы сдвигать всю коррекцию, фактически подстраиваясь под особенности и состояние конкретного образца мотора. Каждая коррекция может изменять впрыск в установленных производителем пределах, и если сумма долгой и краткой коррекций выйдет за общий предел, то обычно ЭБУ сигнализирует об ошибке смесеобразования с помощью индикатора «check engine». ЭБУ обычно использует режим работы с обратной связью по лямбда-зонду до определённого процента расчётной нагрузки на мотор. Далее ЭБУ временно прекращает режим коррекции, так как возникает вероятность неэффективной коррекции, и в этих условиях использование карт впрыска оказывается предпочтительным.

Поскольку некоторое количество кислорода должно присутствовать в выхлопе для нормального дожигания СО и СН^{[неизвестный термин]} в катализаторе, для более точного регулирования может использоваться и второй лямбда-зонд, расположенный за катализатором или внутри него.

Широкополосный лямбда-зонд

Разновидность кислородного датчика.

Основная разница зонда с широким диапазоном измерения по отношению к обычным узкополосным λ-зондам — это комбинация сенсорных ячеек и так называемых накачивающих ячеек. Состав его газового содержимого постоянно соответствует λ=1, что для сенсорной ячейки значит напряжение в 450 милливольт. Содержание газа в зазоре и вместе с ним напряжение сенсора поддерживаются посредством различных напряжений, прикладываемых к накачивающей ячейке. При бедной смеси и напряжении сенсора ниже 450 милливольт ячейка выкачивает кислород из диффузионной полости. Если смесь богатая и напряжение лежит выше 450 милливольт, ток меняет своё направление, и накачивающие ячейки транспортируют кислород в диффузионные расщелины. При этом интегрированный нагревающий элемент устанавливает температуру области от 700 до 800 градусов. Датчик типа LSU при погружении в несгоревшую смесь, содержащую одновременно и топливо и кислород, будет указывать «избыток воздуха», в отличие от порогового, сигнал которого надо интерпретировать «избыток топлива».

Выходной сигнал широкодиапазонного датчика зависит от его контроллера управления, может быть токовым или потенциальным. Например, выходной ток контроллера широкополосного датчика I_pn и соответствующие значения λ^[1]:

Ipn, мА	−5.000	−4.000	−3.000	−2.000	−1.000	−0.500	0.000	0.500	1.000	1.500	2.000	2.500	3.000	4.000
λ	0.673	0.704	0.753	0.818	0.900	0.948	1.000	1.118	1.266	1.456	1.709	2.063	2.592	5.211

Основным преимуществом широкополосного зонда по отношению к узкополосному является устранение циклического перехода дискретных показаний «бедная смесь — богатая смесь». Блок управления получает информацию о степени несоответствия смеси оптимальному значению, и это ему позволяет точнее и быстрее корректировать смесь для достижения её полного сгорания без свободного кислорода.

Примечания

Ссылки

исчисление — это… Что такое Лямбда-исчисление?

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.

λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию. λ-исчисление реализовано Джоном Маккарти в языке Лисп. Вначале реализация идеи λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.

Чистое λ-исчисление

Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами (обами), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличия каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если  — выражение, свободно содержащее , тогда запись означает: функция от аргумента , которая имеет вид , обозначает функцию . Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы свободно входило в , не очень существенно — достаточно предположить, что , если это не так.

β-редукция

Поскольку выражение обозначает функцию, ставящую в соответствие каждому значение , то для вычисления выражения

,

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм вместо переменной . В результате получается . Это соображение в общем виде записывается как

и носит название β-редукция. Выражение вида , то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

η-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применённые к любому аргументу, дают одинаковые результаты. η-преобразование переводит друг в друга формулы и (в обратную сторону — только если не имеет свободных вхождений в : иначе свободная переменная после преобразования станет связанной внешней абстракцией).

Функция двух переменных и может быть рассмотрена как функция одной переменной , возвращающая функцию одной переменной , то есть как выражение . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D → D до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n — 1).

В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого, аргумент, ссылающийся на себя (здесь обозначен как r), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз. Так как существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))

В лямбда-исчислении, Y g — неподвижная точка g; продемонстрируем это:

Y g

λh.((λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g).

Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g) n, где n — число, для которого вычисляется факториал. Пусть n = 4, получаем:

   g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции.

См. также

Примечания

1. ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.
• Чечулин В. Л. О непротиворечивости лямбда-исчисления // В мире научных открытий, серия Математика. Механика. Информатика, 2011, № 1, сс. 203—206

функция — это… Что такое лямбда-функция?



лямбда-функция

мат. lambda function

Большой англо-русский и русско-английский словарь. 2001.

• лямбда-распределение
• лямбдаграмма

Смотреть что такое «лямбда-функция» в других словарях:

• Лямбда-функция — в математике представляет собой показательную функцию, у которой число x возведено в степень самого себя, возведённого в (b−1): Если b стремится к бесконечности, то лямбда функция стремится к 1 при |x| < 1, и к бесконечности при x > 1.… …   Википедия

• Лямбда-выражения — Лямбда выражение (в программировании)  это специальный синтаксис для объявления анонимных функторов по месту их использования. Используя лямбда выражения, можно объявлять функции в любом месте кода. Обычно лямбда выражение допускает… …   Википедия

• Лямбда-исчисление — (λ исчисление)  формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости. λ исчисление может рассматриваться как семейство прототипных языков программирования. Их основная… …   Википедия

• Лямбда исчисление — (λ исчисление, лямбда исчисление) формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости. λ исчисление может рассматриваться как семейство прототипных языков программирования. Их… …   Википедия

• Лямбда-выражение — В программировании лямбда или лямбда выражения это безымянная функция, объявляемая по месту ее непосредственного использования. Обычно лямбда допускает замыкание на лексический контекст, в котором она объявлена. Смотри также Лямбда исчисление… …   Википедия

• Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения …   Википедия

• Функция высшего порядка — Функция высшего порядка  функция, принимающая в качестве аргументов другие функции или возвращающая другую функцию в качестве результата. Основная идея состоит в том, что функции имеют тот же статус, что и другие объекты данных.… …   Википедия

• Однородная функция — степени   числовая функция такая, что для любого и выполняется равенство: причём называют порядком однородности. Различают также положительно однородные функции, для которых равенство …   Википедия

• Рекурсивная функция (теория вычислимости) — У этого термина существуют и другие значения, см. Рекурсивная функция (значения). Термин рекурсивная функция в теории вычислимости используется для обозначения трёх классов функций примитивно рекурсивные функции; общерекурсивные функции; …   Википедия

• Примитивно рекурсивная функция — Термин рекурсивные функции в теории вычислимости используют для обозначения трёх множеств функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с множеством вычислимых по Тьюрингу… …   Википедия

• Частично рекурсивная функция — Термин рекурсивные функции в теории вычислимости используют для обозначения трёх множеств функций примитивно рекурсивные функции; общерекурсивные функции; частично рекурсивные функции. Последние совпадают с множеством вычислимых по Тьюрингу… …   Википедия

исчисление — это… Что такое Лямбда-исчисление?

Ля́мбда-исчисле́ние (λ-исчисление) — формальная система, разработанная американским математиком Алонзо Чёрчем, для формализации и анализа понятия вычислимости.

λ-исчисление может рассматриваться как семейство прототипных языков программирования. Их основная особенность состоит в том, что они являются языками высших порядков. Тем самым обеспечивается систематический подход к исследованию операторов, аргументами которых могут быть другие операторы, а значением также может быть оператор. Языки в этом семействе являются функциональными, поскольку они основаны на представлении о функции или операторе, включая функциональную аппликацию и функциональную абстракцию. λ-исчисление реализовано Джоном Маккарти в языке Лисп. Вначале реализация идеи λ-исчисления была весьма громоздкой. Но по мере развития Лисп-технологии (прошедшей этап аппаратной реализации в виде Лисп-машины) идеи получили ясную и четкую реализацию.

Чистое λ-исчисление

Это простейший из семейства прототипных языков программирования, чистое λ-исчисление, термы которого, называемые также объектами (обами), или λ-термами, построены исключительно из переменных применением аппликации и абстракции. Изначально наличия каких-либо констант не предполагается.

Аппликация и абстракция

В основу λ-исчисления положены две фундаментальные операции:

• Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если  — выражение, свободно содержащее , тогда запись означает: функция от аргумента , которая имеет вид , обозначает функцию . Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы свободно входило в , не очень существенно — достаточно предположить, что , если это не так.

β-редукция

Поскольку выражение обозначает функцию, ставящую в соответствие каждому значение , то для вычисления выражения

,

в которое входят и аппликация и абстракция, необходимо выполнить подстановку числа 3 в терм вместо переменной . В результате получается . Это соображение в общем виде записывается как

и носит название β-редукция. Выражение вида , то есть применение абстракции к некому терму, называется редексом (redex). Несмотря на то, что β-редукция по сути является единственной «существенной» аксиомой λ-исчисления, она приводит к весьма содержательной и сложной теории. Вместе с ней λ-исчисление обладает свойством полноты по Тьюрингу и, следовательно, представляет собой простейший язык программирования.

η-преобразование

η-преобразование выражает ту идею, что две функции являются идентичными тогда и только тогда, когда, будучи применённые к любому аргументу, дают одинаковые результаты. η-преобразование переводит друг в друга формулы и (в обратную сторону — только если не имеет свободных вхождений в : иначе свободная переменная после преобразования станет связанной внешней абстракцией).

Функция двух переменных и может быть рассмотрена как функция одной переменной , возвращающая функцию одной переменной , то есть как выражение . Такой приём работает точно так же для функций любой арности. Это показывает, что функции многих переменных могут быть выражены в λ-исчислении и являются «синтаксическим сахаром». Описанный процесс превращения функций многих переменных в функцию одной переменной называется карринг (также: каррирование), в честь американского математика Хаскелла Карри, хотя первым его предложил М. Э. Шейнфинкель (1924).

Семантика бестипового λ-исчисления

Тот факт, что термы λ-исчисления действуют как функции, применяемые к термам λ-исчисления (то есть, возможно, к самим себе), приводит к сложностям построения адекватной семантики λ-исчисления. Чтобы придать λ-исчислению какой-либо смысл, необходимо получить множество D, в которое вкладывалось бы его пространство функций D → D. В общем случае такого D не существует по соображениям ограничений на мощности этих двух множеств, D и функций из D в D: второе имеет бо́льшую мощность, чем первое.

Эту трудность в начале 1970-х годов преодолел Дана Скотт, построив понятие области D (изначально на полных решётках^[1], в дальнейшем обобщив до полного частично упорядоченного множества со специальной топологией) и урезав D → D до непрерывных в этой топологии функций^[2]. На основе этих построений была создана денотационная семантика языков программирования, в частности, благодаря тому, что с помощью них можно придать точный смысл таким двум важным конструкциям языков программирования, как рекурсия и типы данных.

Связь с рекурсивными функциями

Рекурсия — это определение функции через себя; на первый взгляд, лямбда-исчисление не позволяет этого, но это впечатление обманчиво. Например, рассмотрим рекурсивную функцию, вычисляющую факториал:

f(n) = 1, if n = 0; else n × f(n — 1).

В лямбда-исчислении, функция не может непосредственно ссылаться на себя. Тем не менее, функции может быть передан параметр, связанный с ней. Как правило, этот аргумент стоит на первом месте. Связав его с функцией, мы получаем новую, уже рекурсивную функцию. Для этого, аргумент, ссылающийся на себя (здесь обозначен как r), обязательно должен быть передан в тело функции.

g := λr. λn.(1, if n = 0; else n × (r r (n-1)))

f := g g

Это решает специфичную проблему вычисления факториала, но решение в общем виде также возможно. Получив лямбда-терм, представляющий тело рекурсивной функции или цикл, передав себя в качестве первого аргумента, комбинатор неподвижной точки возвратит необходимую рекурсивную функцию или цикл. Функции не нуждаются в явной передаче себя каждый раз. Так как существует несколько определений комбинаторов неподвижной точки. Самый простой из них:

Y = λg.(λx.g (x x)) (λx.g (x x))

В лямбда-исчислении, Y g — неподвижная точка g; продемонстрируем это:

Y g

λh.((λx.h (x x)) (λx.h (x x))) g

(λx.g (x x)) (λx.g (x x))

g ((λx.g (x x)) (λx.g (x x)))

g (Y g).

Теперь, чтобы определить факториал, как рекурсивную функцию, мы можем просто написать g (Y g) n, где n — число, для которого вычисляется факториал. Пусть n = 4, получаем:

   g (Y g) 4
   (λfn.(1, if n = 0; and n·(f(n-1)), if n>0)) (Y g) 4
   (λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0)) 4
   1, if 4 = 0; and 4·(g(Y g) (4-1)), if 4>0
   4·(g(Y g) 3)
   4·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 3)
   4·(1, if 3 = 0; and 3·(g(Y g) (3-1)), if 3>0)
   4·(3·(g(Y g) 2))
   4·(3·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 2))
   4·(3·(1, if 2 = 0; and 2·(g(Y g) (2-1)), if 2>0))
   4·(3·(2·(g(Y g) 1)))
   4·(3·(2·(λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 1)))
   4·(3·(2·(1, if 1 = 0; and 1·((Y g) (1-1)), if 1>0)))
   4·(3·(2·(1·((Y g) 0))))
   4·(3·(2·(1·((λn.(1, if n = 0; and n·((Y g) (n-1)), if n>0) 0))))
   4·(3·(2·(1·(1, if 0 = 0; and 0·((Y g) (0-1)), if 0>0))))
   4·(3·(2·(1·(1))))
   24

Каждое определение рекурсивной функции может быть представлено как неподвижная точка соответствующей функции, следовательно, используя Y, каждое рекурсивное определение может быть выражено как лямбда-выражение. В частности, мы можем определить вычитание, умножение, сравнение натуральных чисел рекурсивно.

В языках программирования

В языках программирования под «λ-исчислением» зачастую понимается механизм «анонимных функций» — callback-функций, которые можно определить прямо в том месте, где они используются, и которые имеют доступ к локальным переменным текущей функции.

См. также

Примечания

1. ↑ Scott D.S. The lattice of flow diagrams.— Lecture Notes in Mathematics, 188, Symposium on Semantics of Algorithmic Languages.— Berlin, Heidelberg, New York: Springer-Verlag, 1971, pp. 311—372.
2. ↑ Scott D.S. Lattice-theoretic models for various type-free calculi. — In: Proc. 4th Int. Congress for Logic, Methodology, and the Philosophy of Science, Bucharest, 1972.

Литература

• Барендрегт X. Ламбда-исчисление. Его синтаксис и семантика: Пер. с англ. — М.: Мир, 1985. — 606 с.
• Чечулин В. Л. О непротиворечивости лямбда-исчисления // В мире научных открытий, серия Математика. Механика. Информатика, 2011, № 1, сс. 203—206

Лямбда (буква) — это… Что такое Лямбда (буква)?



Лямбда (буква)

Лямбда (буква)

Λλ

Λ, λ (название: ля́мбда, греч. λάμδα) — 11-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 30. Происходит от финикийской буквы — ламед. От буквы «лямбда» произошли латинская буква L и кириллическая Л, а также их производные.

Использование

Прописная Λ

Строчная λ

Лямбда в культуре

• В вымышленной вселенной «Звездных Войн» существует космический корабль, известный как «корабль класса Лямбда», похожий на букву «λ», если смотреть вдоль оси симметрии.
• В серии популярных компьютерных игр Half-Life лямбда является логотипом «Комплекса Лямбда», части исследовательского центра Чёрная Меза, в котором изучаются технологии телепортации. Позднее в игре лямбда становится символом сопротивления людей против инопланетного Альянса. Символ также стал символом серии Half-life и часто используется в названии «Half-Life», заменяя букву «a»( H λ L F — L I F E ). Помимо этого, Лямбда заменят букву «А» в названиях модов и различных роликов. Этот символ присутствует и на костюме главного героя — Гордона Фримена.
• В песне Михаила Щербакова «Австралия» лирический герой мечтал дать имя «Лямбда» своему так и не заведённому жирафу, муравьеду или кенгуру.
• Строчная буква лямбда используется в качестве одного из символов ЛГБТ-движения. В 1970 году она была выбрана как символ кампании за легализацию гомосексуальных отношений.

Wikimedia Foundation. 2010.

• Windows Internet Name Service
• Кеторолак

Смотреть что такое «Лямбда (буква)» в других словарях:

• буква — Знак (азбучный), письмена (множ. ч.), иероглиф (гиероглиф), каракуля, руны. Нагородил какие то каракули, и читай. .. Ср. знак… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. буква …   Словарь синонимов

• Буква Л — Буква кириллицы Л Кириллица А Б В Г Ґ Д …   Википедия

• лямбда — сущ., кол во синонимов: 1 • буква (103) Словарь синонимов ASIS. В.Н. Тришин. 2013 …   Словарь синонимов

• Лямбда — Греческий алфавит Αα Альфа Νν Ню …   Википедия

• Лямбда (символ) — Греческий алфавит Α α альфа Β β бета …   Википедия

• Лямбда-барион — Лямбда барионы (Λ барионы, Λ частицы) группа элементарных частиц, представляющих собой барион с изотопическим спином 0, содержащих ровно два кварка первого поколения (u и d кварк). В состав Λ барионов входит ровно один кварк второго или третьего… …   Википедия

• Лямбда — (Ламбда, Λ, λ) одиннадцатая буква греческого алфавита; как числовой знак 30. Название от семитического lamed острие (жало) …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• лямбда — (др.–греч. Λ, λ λαμβδα) 11 я буква греческого алфавита; с верхним штрихом справа обозначала число 30 , со штрихом внизу слева 30000 …   Словарь лингвистических терминов Т.В. Жеребило

• Люди (буква) — Буква кириллицы Л Кириллица А Б В Г Ґ Д …   Википедия

• Альфа (буква) — У этого термина существуют и другие значения, см. Альфа (значения). Греческий алфавит Αα Альфа …   Википедия