Калькулятор соединения резисторов онлайн. Параллельное соединение резисторов

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Параллельное соединение: общая информация

Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь

потребуется рассчитать сопротивление , используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления

Универсальная схема расчета

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель , то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчёта

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=

1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте

определить общую мощность можно следующим образом : мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Видео: Правильное подключение светодиодов

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью , где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно , можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов.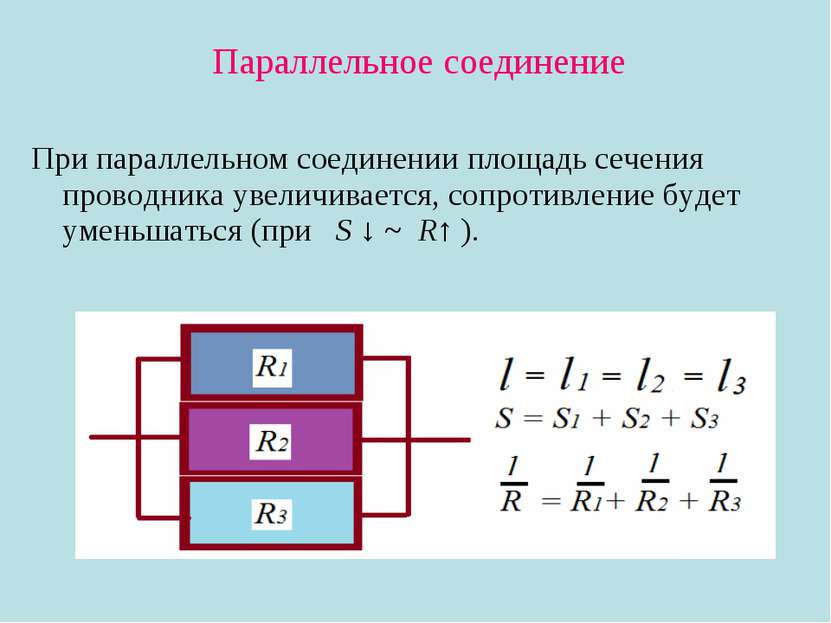 Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов (I1 и I2) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать .

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно.

Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R , то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений.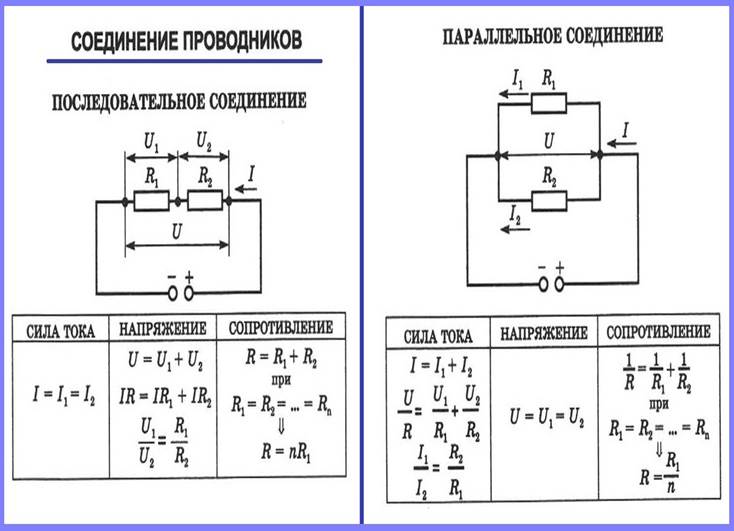 Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства . Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.

Расчет общего сопротивления при параллельном соединении резисторов

В отличие от последовательного соединения, где для нахождения общего сопротивления достаточно сложить значение каждого элемента, для параллельного то же самое будет справедливо для проводимости. А так как она обратно пропорциональна сопротивлению, получим формулу, представленную вместе со схемой на следующем рисунке:

Необходимо отметить одну важную особенность расчета параллельного соединения резисторов: общее значение будет всегда меньше, чем самое маленькое из них. Для резисторов справедливо как для постоянного, так и для переменного тока. Катушки и конденсаторы имеют свои особенности.

Сила тока и напряжение

При расчете параллельного сопротивления резисторов необходимо знать, как рассчитать напряжение и силу тока. В этом случае нам поможет закон Ома, определяющий связь между сопротивлением, силой тока и напряжением.

Исходя из первой формулировки закона Кирхгофа, получим, что сумма сходящихся в одном узле токов равна нулю. Направление выбираем по направлению протекания тока. Таким образом, положительным направлением для первого узла можно считать входящий ток от источника питания. А отрицательными будут отходящие из каждого резистора. Для второго узла картина противоположна. Исходя из формулировки закона, получим, что суммарный ток равен сумме токов, проходящих через каждый параллельно соединенный резистор.

Итоговое напряжение же определяется по второму закону Кирхгофа. Оно одинаково для каждого резистора и равно общему. Эта особенность используется для подключения розеток и освещения в квартирах.

Пример расчета

В качестве первого примера приведем расчет сопротивления при параллельном соединении одинаковых резисторов. Сила тока, протекающая через них, будет одинаковой. Пример расчета сопротивления выглядит так:

По этому примеру прекрасно видно, что общее сопротивление ниже в два раза, чем каждое из них. Это соответствует тому, что суммарная сила тока в два раза выше, чем у одного. А также прекрасно соотносится с увеличением проводимости в два раза.

Второй пример

Рассмотрим пример параллельного соединения трех резисторов. Для расчета используем стандартную формулу:

Похожим образом рассчитываются схемы с большим количеством параллельно соединенных резисторов.

Пример смешанного соединения

Для смешанного соединения, например, представленного ниже, расчет будет производиться в несколько этапов.

Для начала последовательные элементы можно условно заменить одним резистором, обладающим сопротивлением, равным сумме двух заменяемых. Далее общее сопротивление считаем тем же способом, что и для предыдущего примера. Данный метод подойдет и для других более сложных схем. Последовательно упрощая схему, можно получить необходимое значение.

Например, если вместо резистора R3 будут подключены два параллельных, потребуется сначала рассчитать их сопротивление, заменив их эквивалентным. А далее то же самое, что и в примере выше.

Применение параллельной схемы

Параллельное соединение резисторов находит свое применение во многих случаях. Последовательное подключение увеличивает сопротивление, а для нашего случая оно уменьшится. Например, для электрической цепи требуется сопротивление в 5 Ом, но есть только резисторы на 10 Ом и выше. Из первого примера мы знаем, что можно получить в два раза меньшее значение сопротивления, если установить два одинаковых резистора параллельно друг другу.

Уменьшить сопротивление можно еще больше, например, если две пары параллельно соединенных резисторов соединить параллельно относительно друг друга. Можно уменьшить сопротивление еще в два раза, если резисторы имеют одинаковое сопротивление. Комбинируя с последовательным соединением, можно получить любое значение.

Второй пример — это использование параллельного подключения для освещения и розеток в квартирах. Благодаря такому подключению напряжение на каждом элементе не будет зависеть от их количества и будет одинаковым.

Еще один пример использования параллельного подключения — это защитное заземление электрооборудования. Например, если человек касается металлического корпуса прибора, на который произойдет пробой, получится параллельное соединения его и защитного проводника. Первым узлом будет место прикосновения, а вторым нулевая точка трансформатора. По проводнику и человеку будет течь разный ток. Величину сопротивления последнего принимают за 1000 Ом, хотя реальное значение зачастую гораздо больше. Если бы не было заземления, весь ток, протекающий в схеме, пошел бы через человека, так как он был бы единственным проводником.

Параллельное соединение может использоваться и для батарей. Напряжение при этом остается прежним, однако в два раза возрастает их емкость.

Итог

При подключении резисторов параллельно, напряжение на них будет одинаковым, а ток равен сумме протекающих через каждый резистор. Проводимость будет ровняться сумме каждого. От этого и получается необычная формула суммарного сопротивления резисторов.

Необходимо учитывать при расчете параллельного соединения резисторов то, что итоговое сопротивление будет всегда меньше самого маленького. Это также можно объяснить суммированием проводимости резисторов. Последняя будет возрастать при добавлении новых элементов, соответственно и проводимость будет уменьшаться.

Калькулятор параллельного сопротивления — электротехника и электроника

Калькулятор параллельных сопротивлений

Вычислите общее сопротивление резисторов параллельно с легкостью!

Вывод

Эквивалентное сопротивление

(Ω)

Как вычислить общее сопротивление резисторов в параллельном

Вычисление эквивалентного сопротивления (R _EQ ) резисторов параллельно вручную может быть утомительным. Этот инструмент был разработан, чтобы помочь вам быстро вычислить эквивалентное сопротивление, независимо от того, имеете ли вы два или десять резисторов параллельно. Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.

Вы можете легко вычислить эквивалентное сопротивление, если параллельно два идентичных резистора: это половина индивидуального сопротивления. Это удобно, когда вам нужно определенное значение сопротивления и у него нет подходящей части. Например, если вы знаете, что вам нужно около 500 Ом, чтобы получить желаемую яркость из светодиодной схемы, вы можете использовать два резистора 1 кОм параллельно.

Имейте в виду, что ток через индивидуальный резистор не изменяется, когда вы добавляете резисторы параллельно, потому что одновременное добавление резисторов не влияет на напряжение на клеммах резисторов. Какими изменениями является общий ток, подаваемый источником питания, а не ток через один конкретный резистор.

уравнения

$$ \ frac {1} {R_ {EQ}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + … + \ frac {1} {R_ {N}} $$

Когда параллельно параллельно два резистора: $$ R_ {EQ} = \ frac {R_1 \ times R_2} {R_1 + R_2} $$

Приложения

Резисторы в серии эквивалентны одному резистору, сопротивление которого является суммой каждого отдельного резистора. С другой стороны, резисторы, в свою очередь, приводят к эквивалентному сопротивлению, которое всегда ниже каждого отдельного резистора. Если вы думаете об этом, это имеет смысл: если вы применяете напряжение на резисторе, то происходит определенное количество текущих потоков. Если вы добавите еще один резистор параллельно с первым, вы по существу открыли новый канал, через который может протекать больше тока. Независимо от того, насколько величен второй резистор, общий ток, протекающий от источника питания, будет по меньшей мере немного выше, чем ток через один резистор. И если общий ток выше, общее сопротивление должно быть ниже.

Дальнейшее чтение

• Учебник — Простые параллельные схемы
• Техническая статья — Сопротивление в параллельных сетях
• Параллельные схемы видеосигналов

Калькулятор | ColorAndCode

 

LCD1602/2004 — HD44780
Параллельное соединение резисторов   Двойное нажатие на введенное значение в списке позволяет его отредактировать.
Последовательное соединение резисторов   Двойное нажатие на введенное значение в списке позволяет его отредактировать.
Параллельное соединение конденсаторов   Двойное нажатие на введенное значение в списке позволяет его отредактировать.
Последовательное соединение конденсаторов   Двойное нажатие на введенное значение в списке позволяет его отредактировать.
Реактивное сопротивление конденсатора
Реактивное сопротивление конденсатора (+)
Реактивное сопротивление катушки индуктивности
Реактивное сопротивление катушки индуктивности (+)
Обратное определение при параллельном соединении резисторов и последовательном конденсаторов
Определение индуктивности из частоты и реактивного сопротивления
Определение емкости из частоты и реактивного сопротивления
Проводники
Цилиндрические однослойные катушки
Цилиндрические однослойные катушки (+)
Тороидальные катушки на ферритовых кольцах     Дополнительно: — Возможность использовать данные из справочника.
Программирование ДПКД (делитель с переменным коэффициентом деления)
Сопротивление резистора для светодиода   Дополнительно: — Возможность использовать данные из справочника; — Вывод номинала в 4-х цветной маркировке для ряда E24 +/- 5 %.
Расчёт схемы на основе NE555
Расчёт схем на основе LM317, LM338, LM350
Расчёт схем на основе LM2596
Расчет катушек на ферритовых кольцах фирмы Amidon
Расчёт индуктивности квадратной плоской катушки
Индуктивность прямого провода над проводящей подложкой

 

Дополнительный материал в статье:

— Полупроводниковая светотехника № 4 за 2019 год

— Радиолюбитель № 3 за 2010 год

— Компоненты и технологии № 6 за 2010 год

Расчет параллельного соединения резисторов калькулятор онлайн

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов.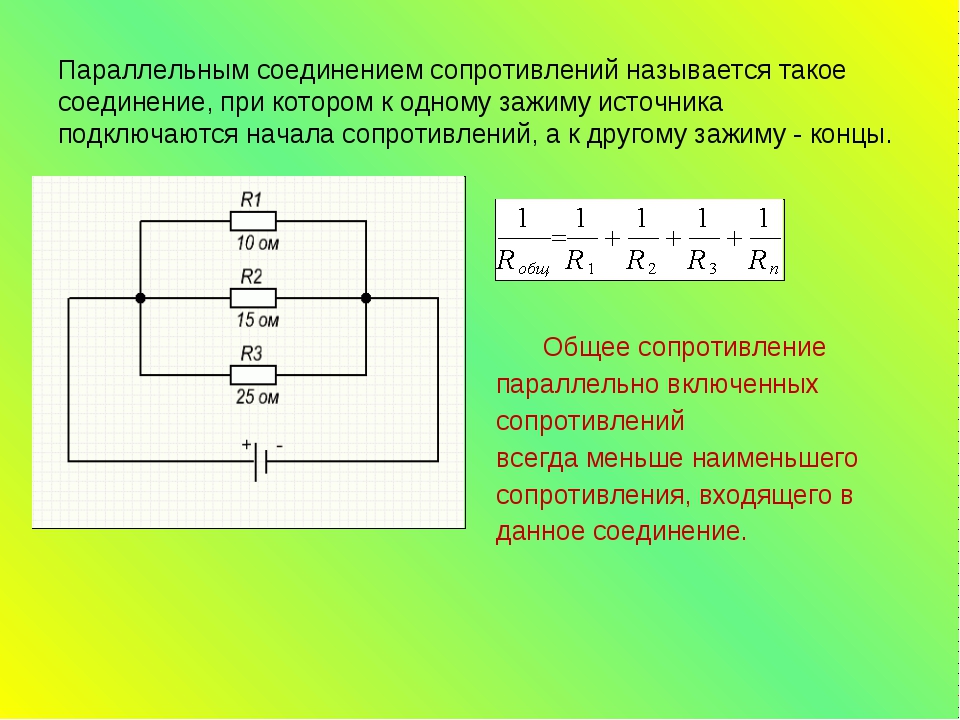 Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.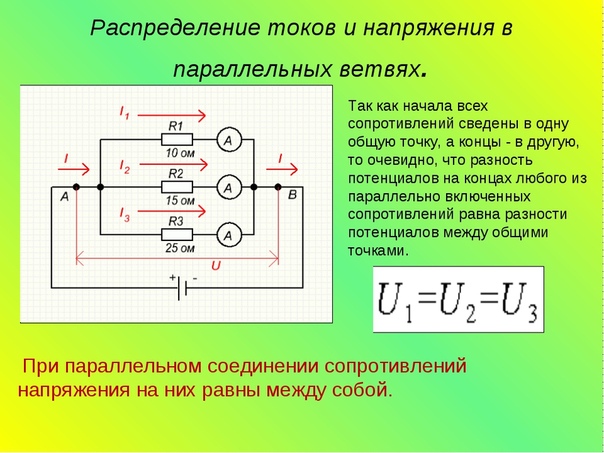

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор расчёта параллельного соединения резисторов

Вычислить сопротивление нескольких параллельно соединённых резисторов (до 10)

Впишите любое количество любых номиналов в омах и кликните мышкой в таблице.

Выбрать два имеющихся в наличии номинала E24 и получить результат их параллельного соединения

Если нужен номинал R и имеем резисторы стандарта E24 (+/-5%), тогда вписываем R и кликаем мышкой в таблице. Получим варианты параллельного соединения резисторов R₁ и R₂.

Ещё один калькулятор более точного подбора номинала из резисторов стандарта E48 (+/-2%).

Подбираем (меняем) нужный номинал из того что есть.

Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств.

Замечания и предложения принимаются и приветствуются!

Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:

Параллельное соединение резисторов

Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.

Для этого вам необходимо:

• Указать в графе «количество резисторов» их число, в нашем примере их три;
• После того, как вы укажите количество элементов, в поле ниже появится три окошка для ввода значения сопротивления каждого из элементов, к примеру, у вас резисторы сопротивлением 20, 30 и 60 Ом;
• Далее нажмите кнопку «рассчитать» и в окошке «параллельное сопротивление в цепи» вы получите значение сопротивления в 10 Ом.

Чтобы рассчитать другую цепь или при подборе других элементов, нажмите кнопку «сбросить», чтобы обнулить значение параллельно включенных элементов калькулятора.

Для расчета суммарного сопротивления калькулятором используется такое соотношение:

• R_сум — суммарное сопротивление параллельно соединенных элементов
• R₁ — сопротивление первого резистора;
• R₂ — сопротивление второго резистора;
• R₃ — сопротивление третьего резистора;
• R_n — сопротивление n-ого элемента.

Таким образом, в рассматриваемом примере параллельно включены три резистора, поэтому формула для определения суммарного сопротивления будет иметь такой вид:

Чтобы выразить величину суммарного сопротивления необходимо умножить обе половины уравнения на произведение сопротивлений всех трех резисторов. После этого перенести составляющие элементы по правилу пропорции и получить значение сопротивления:

Как видите, расчет параллельного сопротивления резисторов вручную требует немалых усилий, поэтому куда проще его сделать на нашем онлайн калькуляторе.

Обратите внимание, при наличии элементов с сопротивлением в разной размерности Ом, кОм, МОм, их необходимо привести к одной величине, прежде чем производить расчет. К примеру, в Ом и указывать в поле калькулятора для расчета параллельного соединения резисторов значение непосредственно в Омах.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Конвертер величин

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Последовательное и параллельное соединение проводников, резисторов,

конденсаторов и катушек индуктивности. Онлайн расчёты.

«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно. Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »

«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью. »

Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо. », а заодно набросаю пару-тройку калькуляторов на заданную тему.

Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.

Рис.1

Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить.
Короче, все вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников

Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.

Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.

Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:

С = С 1 + С 2 +. + С n и 1/L = 1/L 1 + 1/L 2 +. + 1/L n для параллельных цепей и
L = L 1 + L 2 +. + L n и 1/С = 1/С 1 + 1/С 2 +. + 1/С n для последовательных.

Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.

РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов

Ну и в завершении ещё одна таблица.

РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек

Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.

Расчет сопротивления параллельного соединения резисторов

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Расчет сопротивления резистора для светодиодов: онлайн-калькулятор

Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы диод работал правильно и не перегорел, его нельзя подключать напрямую в питающую сеть. Дело в том, что он имеет низкое внутреннее сопротивление, потому если подключить его напрямую, то сила тока окажется высокой, и он перегорит. Ограничить силу тока можно резисторами. Но нужно подобрать правильный резистор для светодиода. Для этого проводятся специальные расчеты.

Расчет резистора для светодиода

Чтобы компенсировать сопротивление светодиода, нужно прежде всего подобрать резистор с более высоким сопротивлением. Такой расчет не составит труда для тех, кто знает, что такое закон Ома.

Математический расчет

Исходя из закона Ома, рассчитываем по такой формуле:

где Un – напряжение сети; Uvd – напряжение, на которое рассчитана работа светодиода; Ivd – ток.

Допустим, у нас светодиод с характеристиками:

2,1 -3, 4 вольт – рабочее напряжение (Uvd). Возьмем среднее значение 2, 8 вольт.

20 ампер – рабочий ток (Ivd)

220 вольт – напряжение сети (Un)

В таком случае мы получаем величину сопротивления R = 10, 86. Однако этих расчетов недостаточно. Резистор может перегреваться. Для предотвращения перегрева нужно учитывать при выборе его мощность, которая рассчитывается по следующей формуле:

Для наглядности рекомендуем посмотреть видео:

Графический расчет

Графический способ – менее популярный для расчета резистора на светодиод, но может быть даже более удобный. Зная напряжение и ток диода (их называют еще вольтамперными характеристиками – ВАХ), вы можете узнать сопротивление нужного резистора по графику, представленному ниже:

Тут изображен расчет для диода с номинальным током 20мА и напряжением источника питания 5 вольт. Проводя пунктирную линию от 20 мА до пересечения с «кривой led» (синий цвет), чертим пересекающую линию от прямой Uled до прямой и получаем максимальное значение тока около 50 мА. Далее рассчитываем сопротивление по формуле:

Получаем значение 100 Ом для резистора. Находим для него мощность рассеивания (Силу тока берем из Imax):

Онлайн-калькулятор расчета сопротивления

Задача усложняется, если вы хотите подключить не один, а несколько диодов.

Для облегчения самостоятельных расчетов мы подготовили онлайн-калькулятор расчета сопротивления резисторов. Если подключать несколько светодиодов, то нужно будет выбрать между параллельным и последовательным соединениями между ними. И для этих схем нужны дополнительные расчеты для источника питания. Можно их легко найти в интернете, но мы советуем воспользоваться нашим калькулятором.

Вам понадобится знать:

1. Напряжение источника питания.
2. Характеристику напряжения диода.
3. Характеристику тока диода.
4. Количество диодов.

А также нужно выбрать параллельную или последовательную схему подключения. Рекомендуем ознакомиться с разницей между соединениями в главах, которые мы подготовили ниже.

В каких случаях допускается подключение светодиода через резистор

Никакие диоды, в том числе светодиоды, нельзя включать без ограничения проходящего тока. Резисторы в таком случае просто необходимы. Даже небольшое изменения напряжения вызывают очень сильное изменение тока и, следовательно, перегрев диода.

Параллельное соединение

Для тех, кто уже сталкивался на практике со схемами подключения светодиодного освещения, вопрос о выборе между параллельным и последовательным соединением обычно не стоит. Чаще всего выбирают схему последовательного соединения. У параллельного соединения для светодиодов есть один важный недостаток – это удорожание и усложнение конструкции, потому что для каждого диода нужен отдельный резистор. Но такая схема имеет и большой плюс – если сгорела одна линия, то перестанет светить только один диод, остальные продолжат работу.

Почему нельзя использовать один резистор для нескольких параллельных диодов

Объясняется достаточно просто: если перегорит один светодиод, то на другой (-ие) может попасть больший ток и начнется перегрев. Потому при параллельной схеме подключения каждому диоду нужен отдельный резистор.

Последовательное соединение светодиодов

Именно такое соединение пользуется популярностью. Объясняется такой частый выбор простым примером. Представьте, что в елочной гирлянде для каждого светодиода подобран резистор. А в гирлянде этих лампочек бывает более сотни! Параллельное соединение в данном случае невыгодно и трудоемко.

Можно ли обойтись без резисторов

В бюджетных или просто старых приборах используются резисторы. Также они используются для подключения всего только нескольких светодиодов.

Но есть более современный способ – это понижение тока через светодиодный драйвер. Так, в светильниках в 90% встречаются именно драйверы. Это специальные блоки, которые через схему преобразуют характеристики тока и напряжения питающей сети. Главное их достоинство – они обеспечивают стабильную силу тока при изменении/колебании входного напряжения.

Сегодня можно подобрать драйвер под любое количество светодиодов. Но рекомендуем не брать китайские аналоги! Кроме того, что они быстрей изнашиваются, ещё могут выдавать не те характеристики в работе, которые заявлены на упаковке.

Если светодиодов не так много, подойдут и резисторы вместо достаточно высокого по цене драйвера.

Интересное видео по теме:

В заключение

Пишите комментарии и делитесь статьей в социальных сетях! Если возникли вопросы, можно найти в интернете дополнительные видео для расчета сопротивления резистора и на другие близкие темы.

последовательное, параллельное, смешанное соединение. Расчет сопротивления

Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.

Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.

ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I₁+I₂+..In

С учетом этого имеем:

• I=U/R
• I₁=U/R₁
• I₂=U/R₂
• In=U/Rn
• U/R=U/R₁+U/R₂+…U/Rn
• 1/R=1/R₁+1/R₂+…1/Rn

Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно: R=(R₁*R₂)/(R₁+R₂).

Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R₁=R₂) их общее сопротивление будет вдвое меньше любого из них. Это полезно помнить.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:

• U=I*R
• I=I₁=I₂=…In
• U=U₁+U₂+…Un
• I*R=I*R₁+I*R₂+…I*Rn
• R=R₁+R₂+…Rn

То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.

СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ

Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.3).

Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:

1. последовательное сопротивление резисторов Rпосл=R₁+R₂
2. параллельное соединение R=(Rпосл*R₃)/(Rпосл+R₃)

Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.

Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:

1. Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.

   Например, для рисунка 3.a, если фактическая погрешность R₁ составляет +10%, а R₂ имеет +15%, то для Rпосл она будет +25%.

   Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.

2. Необходимость получить большую мощность.

   Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.

   В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.

Про мощность и номиналы резисторов можно почитать здесь.

© 2012-2020 г. Все права защищены.

Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов

Параллельная схема: характеристики, преимущества и недостатки

Параллельное соединение проводников

Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

Рисунок 4. Схема параллельного соединения проводников

Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:

I = I₁ + I₂ + I₃.

Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:

то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.

Видео 2. Первый закон Кирхгофа

Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.

Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.

Общий ток, приходящий к точке А, равен:

Токи в каждой из ветвей имеют значения:

По формуле первого закона Кирхгофа

I = I₁ + I₂ + I₃

или

Вынося U в правой части равенства за скобки, получим:

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:

или

g = g₁ + g₂ + g₃.

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 4 Ом.

откуда

Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:

откуда

Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.

Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r₁, деленному на число ветвей n:

Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:

Для проверки попробуем найти сопротивление разветвления по формуле:

откуда

Как видим, ответ получается тот же.

Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.

Рисунок 5. К примеру 6

Найдем общее сопротивление цепи:

откуда

Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).

Падение напряжения на участке между точками А и Б будет:

U = I × r = 22 × 1,09 = 24 В.

Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.

Рассматривая первую ветвь разветвления с сопротивлением r₁, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:

Ток второй ветви

Ток третьей ветви

Проверим по первому закону Кирхгофа

I = I₁ + I₂ + I₃ = 12 + 6 + 4 = 22 А.

Следовательно, задача решена верно.

Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения. Первая ветвь: r1 = 2 Ом, I1 = 12 А

Вторая ветвь: r2 = 4 Ом, I2 = 6 А. Третья ветвь: r3 = 6 Ом, I3 = 4 А

Первая ветвь: r₁ = 2 Ом, I₁ = 12 А. Вторая ветвь: r₂ = 4 Ом, I₂ = 6 А. Третья ветвь: r₃ = 6 Ом, I₃ = 4 А.

Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.

Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.

Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:

или окончательно:

Последовательное соединение ламп накаливания.

Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.

Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.

Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.

Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.

Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.

Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.

Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.

Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.

На следующем рисунке показаны три лампы соединенные последовательно.

На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.

Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.

Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.

P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.

Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.

Вывод:

Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.

А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Примеры использования

• Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
• Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
• Делитель напряжения
• Балласт
• Шунт

Какой способ лучше?

Метод «шлейфов» не слишком удобен только тем, что любой потребитель по цепи зависит от предыдущего. Например, если произойдёт обрыв провода на второй розетке, то третья и четвёртая также останутся без напряжения. Но при этом нельзя не выделить экономию проводника при начальном монтаже электропроводки.

Рисунок 3: Комбинированное соединение розеток

К тому же, «шлейфом» очень удобно проводить линии, когда необходимо минимизировать количество штроб в стенах. А делают это при монтаже проводки по полу или потолку, в специальной гофрированной трубе. Тогда остаётся провести только основные штробы к розеткам и между ними.

Вывод: прокладка электропроводки «шлейфом» удобна и экономична, не занимает много времени в процессе монтажа, имеет длительный эксплуатационный срок и совсем незначительные недостатки, которые можно оставить без внимания.

Последовательное соединение ламп накаливания.

Последовательное соединение ламп накаливания в домашнем быту используется редко. В свое время я подключал две лампы последовательно у себя в подъезде, но это был единичный случай.

Тут ситуация была такая, что подъездная лампа перегорала с периодичностью в один месяц, и надо было что-то делать.

Обычно, в таких случаях лампу включают через диод, чтобы она питалась пониженным напряжением 110В и долго служила. Вариант проверенный, но при этом сама лампа мерцает, да и светит в полнакала.

Когда же стоят две последовательно, то они так же питаются пониженным напряжением 110В, не мерцают, долго служат, светят и потребляют энергии как одна. Причем их можно развести по разным углам помещения, что тоже плюс.Но повторюсь – это редкий случай.

Посмотрите на рисунок ниже. Здесь изображены две схемы последовательного соединения ламп накаливания. В верхней части рисунка показана принципиальная схема, а в нижней части – монтажная. Причем для лучшего восприятия, монтажная схема показана с реальным изображением ламп и двужильного провода.

Здесь в линии коричневого цвета, лампы HL1 и HL2 соединены последовательно – одна за другой. Поэтому такое соединение называют последовательным.

Если подать напряжение питания 220В на концы L и N, то загорятся обе лампы, но гореть они будут не в полную силу, а в половину накала. Так как сопротивление нитей ламп рассчитано на питающее напряжение 220В, и когда они стоят в цепи последовательно, одна за другой, то за счет добавления сопротивления нити накала следующей лампы, общее сопротивление цепи будет увеличиваться, а значит, для следующей лампы напряжение всегда будет меньше согласно закону Ома.

Поэтому при последовательном соединении двух ламп напряжение 220В будет делиться пополам, и составит 110В для каждой.

На следующем рисунке показаны три лампы соединенные последовательно.

На этой схеме напряжение на каждой лампе составит около 73 Вольт, так как будет делиться уже между тремя лампами.

Так же примером последовательного соединения могут служить новогодние гирлянды. Здесь из миниатюрных лампочек с низким питанием создается одна лампа на напряжение 220В.

Например, берем лампочки, рассчитанные на 6,3 Вольта и делим их на 220 Вольт. Получается 35 штук. То есть, чтобы сделать одну лампу на напряжение 220В, нам нужно соединить последовательно 35 штук с напряжением питания 6,3 Вольта.

P.S. Так как напряжение в сети не постоянно, то расчет лучше производить исходя из 245 – 250 Вольт.

Как Вы знаете, у гирлянд есть один недостаток. Перегорает одна из ламп, например, канала зеленого цвета, значит, не горит канал зеленого цвета. Тогда мы идем на базар, покупаем лампочки зеленого цвета, а потом дома по одной вынимаем, вставляем новую, и пока не заработает канал, перебираем его весь.

Вывод:

Недостатком последовательного соединения является то, что если выйдет из строя хоть одна из ламп, гореть не будут все, так как нарушается электрическая цепь.

А вторым недостатком, как Вы уже догадались, является слабое свечение. Поэтому последовательное соединение ламп накаливания на напряжение 220В в домашних условиях практически не применяется.

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Схема параллельного соединения

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * . Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

• Таким образом, протекающий общий ток в цепи  можно определить как:
• I = I1 + I2
• Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
• Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
• Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
• Таким образом, общий ток будет равен:
• I = 0,545 мА + 0,255 мА = 0,8 мА
• Это также можно проверить, используя закон Ома:
• I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
• где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
• И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Последовательное соединение источников питания

Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:

Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.

Если “минус” одной батарейки соединить с “плюсом” другой батарейки, то их общее напряжение суммируется.

Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос – это ЭДС.

Наполовину разряженная батарейка будет уже выглядеть примерно вот так:

Можно сказать, насос уже не справляется.

Батарейка посаженная в “ноль” будет выглядеть вот так:

Насос автоматической подачи воды сломался.

Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:

Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса – черный.

Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.

На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.

Таким же способом замеряем напряжение на аккумуляторе №2

О, как совпало). Те же самые 3,66 Вольт.

Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:

Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.

Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.

Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.

Оцените статью:

Суммарное сопротивление при последовательном соединении. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов. Сопротивление параллельной цепи

Содержание:

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

• Сила тока на всех участках цепи будет одинаковой.
• Общее напряжение цепи составляет сумму напряжений на каждом участке.
• Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.

В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.

Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.

Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.

Законы последовательного и параллельного соединения проводников

Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.

Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:

• Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
• параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
• Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
• При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
• Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.

Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.

Смешанное соединение проводников

В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.

В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.

Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.

Проверим справедливость показанных здесь формул на простом эксперименте.

Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении

Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении

Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:

При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.

Что ещё нужно учитывать при соединении резисторов?

Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?

Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .

Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.

Подробнее о мощности рассеивания резистора читайте .

Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.

Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как alt=»q > 0″> и alt=»A > 0″> , то и alt=»\varphi_a — \varphi_b > 0″> , т. е. alt=»\varphi_a > \varphi_b»> .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6 ).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

Стало быть, через резистор течёт ток A.

Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому

Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).

Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:

Применяя закон Ома для каждого участка цепи, получим:

где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем

Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:

Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .

При последовательном соединении резисторов справедливо соотношение

т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.

Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:

Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:

Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:

Подставляя I, I 1 и I 2 в формулу (2), получим.

Содержание:

Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.

Напряжение при последовательном соединении

При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.

Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: R общ = R 1 + R 2 .

Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.

Напряжение при параллельном соединении

При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.

Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.

На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.

В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.

Калькулятор параллельного сопротивления

— Инструменты для электротехники и электроники

С легкостью рассчитайте общее сопротивление параллельно включенных резисторов!

Как рассчитать полное сопротивление резисторов, включенных параллельно

Расчет эквивалентного сопротивления (R _EQ ) параллельно включенных резисторов вручную может быть утомительным. Этот инструмент был разработан, чтобы помочь вам быстро рассчитать эквивалентное сопротивление, независимо от того, подключены ли у вас два или десять резисторов параллельно.Чтобы использовать его, просто укажите количество параллельных резисторов и значение сопротивления для каждого из них.

Вы можете легко вычислить эквивалентное сопротивление, если у вас есть два идентичных резистора, подключенных параллельно: это половина отдельного сопротивления. Это удобно, когда вам нужно определенное значение сопротивления, а подходящей детали нет в наличии. Например, если вы знаете, что вам нужно около 500 Ом, чтобы получить желаемую яркость светодиодной цепи, вы можете использовать два резистора 1 кОм параллельно.

Имейте в виду, что ток через отдельный резистор не изменяется, когда вы добавляете резисторы параллельно, потому что добавление резисторов параллельно не влияет на напряжение на выводах резисторов. Изменяется общий ток, подаваемый источником питания, а не ток через один конкретный резистор.

Уравнения

$$ \ frac {1} {R_ {EQ}} = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} + … + \ frac {1} {R_ {N}} $$

Когда у вас есть только два параллельно подключенных резистора: $$ R_ {EQ} = \ frac {R_1 \ times R_2} {R_1 + R_2} $$

Приложения

Последовательные резисторы эквивалентны одному резистору, сопротивление которого является суммой каждого отдельного резистора.С другой стороны, параллельное соединение резисторов дает эквивалентное сопротивление, которое всегда ниже, чем у каждого отдельного резистора. Если подумать, это имеет смысл: если вы подаете напряжение на резистор, протекает определенное количество тока. Если вы добавите еще один резистор параллельно первому, вы, по сути, откроете новый канал, по которому может течь больше тока. Независимо от того, насколько велик второй резистор, общий ток, протекающий от источника питания, будет, по крайней мере, немного выше, чем ток через единственный резистор.А если общий ток выше, общее сопротивление должно быть ниже.

Дополнительная литература

Калькулятор параллельных резисторов

R1 + R2 = эквивалентный резистор R схема сопротивления, эквивалентная общая сумма резисторов, упрощенная комбинация = параллельная

параллельная калькуляция резисторов R1 + R2 = эквивалентный резистор R, эквивалентная схема сопротивления, эквивалентная общая схема поиска резисторов, упрощенная комбинация = параллельная — sengpielaudio Sengpiel Berlin

R всего

Формула: R всего = R1 × R2 / (R1 + R2)

Введите два значения резистора , будет рассчитано третье значение параллельной цепи.
Вы даже можете ввести общее сопротивление R _всего и одно известное сопротивление R ₁ или R ₂ .

Формула (уравнение) для расчета двух сопротивлений R ₁ и R ₂ , соединенных параллельно:

Расчет необходимого параллельного резистора R ₂ , когда дается R ₁ и общее сопротивление R _итого :

Решение формулы R итого = ( R 1 × R 2 ) / ( R 1 + R 2 ) для R 1 : Первый шаг — очистить все дроби путем умножения на наименьшее значение . общий знаменатель, то есть R t × R 1 × R 2 … итого получаем: 1/ R итого = 1/ R 1 + 1/ R 2 R итого × R 1 × R 2 [1/ R всего = 1/ R 1 + 1/ R 2 ] R 1 × R 2 = R всего × R 2 + R всего × R 1 затем соберите члены с R 1 и решите R 1 × R 2 — R всего × R 1 = R всего × R 2 R 1 ( R 2 — R всего ) = R 2 × R итого 9001 4 Последний шаг: R 1 = R 2 × R всего / ( R 2 — R всего ) или: R 2 = R 1 × R всего / ( R 1 — R всего )

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно
точно так же, как вычисления, необходимые для параллельных катушек индуктивности или для конденсаторов, включенных последовательно.

Два резистора, включенных параллельно, и результирующее общее сопротивление: Два одинаковых значения, также покажите уравнение, что результаты всегда равны половине. Это упрощает работу, когда проектирование схем или прототипирование. С кепками всегда вдвое больше, потом с кепками всего просто сложите параллельно.

• Поисковые сопротивления R ₁ и R ₂ , когда известно целевое сопротивление (эквивалентное сопротивление) •

Расчет: пары резисторов — вычислитель с обратной конструкцией
Поиск R ₁ и R ₂ с известным целевым сопротивлением

● Рассчитать несколько резисторов параллельно ●

Этот калькулятор определяет сопротивление от до 10 резисторов, включенных параллельно . Введите сопротивления в поля ниже и, когда все значения будут введены, нажмите кнопку «рассчитать», и результат появится в поле под этой кнопкой. В качестве теста, если мы введем сопротивления 4, 6 и 12 Ом, ответ должен быть 2 Ом. Примечание. При снятии флажков вручную сохраненные значения не сбрасываются. Воспользуйтесь «сбросом».

Закон Ома — калькулятор и формулы

Два резистора, включенных параллельно, и результирующее общее сопротивление
Сопротивление в диапазоне от 1 Ом до 100 Ом

R2	R1
	1	1.5	2,2	3,3	4,7	6,8	10	15	22	33	47	68
1	0,5	0,6	0,69	0.77	0,83	0,87	0,91	0,93	0,95	0,97	0,98	0,99
1,5	0,6	0,75	0,89	1,03	1,14	1,22	1,30	1,36	1,40	1,43	1.45	1,46
2,2	0,69	0,89	1,1	1,32	1,50	1,66	1,82	1,92	2,0	2,06	2,10	2,13
3,3	0,77	1,03	1,32	1.65	1,94	2,22	2,48	2,70	2,87	3,00	3,08	3,14
4,7	0,83	1,14	1,50	1,94	2,35	2,78	3,20	3,58	3,87	4,12	4.27	4,39
6,8	0,87	1,22	1,66	2,22	2,78	3,40	4,05	4,68	5,19	5,64	5,94	6,18
10	0,91	1,30	1,82	2.48	3,20	4,05	5,0	6,0	6,9	7,7	8,3	8,7
15	0,93	1,36	1,92	2,70	3,58	4,68	6,0	7,50	8,9	10,3	11,4	12.2
22	0,95	1,40	2,00	2,87	3,87	5,19	6,9	8,9	11,0	13,2	15,0	16,6
33	0,97	1,43	2,06	3,0	4.12	5,64	7,7	10,3	13,2	16,5	19,4	22,2
47	0,98	1,45	2,1	3,08	4,27	5,94	8,3	11,4	15,0	19,4	23,5	27.8
68	0,99	1,46	2,13	3,14	4,39	6,18	8,7	12,2	16,6	22,2	27,8	34,0

Примечание: Этот калькулятор также может решать другие математические задачи. Расчет резисторов параллельно
точно так же, как вычисления, необходимые для параллельных катушек индуктивности или для конденсаторов, включенных последовательно.

Мощность, рассеиваемая в резисторе: P = В × I , P = В 2 / R , P = I 2 × R .

Примечание: Для резисторов, соединенных последовательно, ток одинаков для каждого резистора, а для резисторов, включенных параллельно, напряжение одинаково для каждого резистора.

КАЛЬКУЛЯТОР ПАРАЛЛЕЛЬНОГО РЕЗИСТОРА

Резисторы в параллельном калькуляторе Если вы ищете резистор Калькулятор ЦВЕТОВОГО КОДА, затем кликните сюда. Загрузка Этот калькулятор может определить сопротивление до 10 резисторов, включенных параллельно. Введите сопротивления в поля ниже и когда все значения будут ввода, нажмите кнопку РАССЧИТАТЬ, и результат будет появятся в поле под этой кнопкой. В качестве теста, если вы вводите сопротивления 3, 9 и 18 Ом, ваш ответ должен быть 2 Ом. При нажатии кнопки «СБРОС» все поля очищаются. Этот калькулятор может решать другие математические задачи. Расчет резисторов параллельно ТОЧНО то же самое, что и расчеты, необходимые для ИНДУКТОРОВ в ПАРАЛЛЕЛЬНОМ или для конденсаторов СЕРИИ . Этот калькулятор можно использовать для рабочих задач. Например, «А» может покрасить комнату за 5 часов, а «Б» покрасить комнату за 6 часов. Если они оба работают вместе, сколько времени займет работа? Введите 5 и 6 просто как если бы они были резисторами и получите ответ. Этот калькулятор можно использовать для задач «заполнения». Например, одна труба может наполнить воду бак за 5 часов, в то время как другая труба может заполнить тот же бак за 6 часов. Если обе трубы работают одновременно …….. хммм кажется жутко знакомым к другой проблеме, не так ли? Удачи тебе с математическими задачами. Числа отображаются в экспоненциальном представлении с указанием количества значащие цифры, которые вы указываете. Для удобства чтения числа от 0,001 до 1000. будет не в экспоненциальной нотации, но все равно будет иметь ту же точность. Вы можете изменить количество значащих цифр, отображаемых изменение числа в поле выше. Большинство браузеров будут отображать ответы правильно, но если вы вообще не видите ответов, введите ноль в поле выше, что приведет к исключите все форматирование, но, по крайней мере, вы увидите ответы. Вернуться на главную страницу Авторские права © 1999 — 1728 Программные системы

Как рассчитать резисторы, включенные последовательно и параллельно — Kitronik Ltd

Резисторы серии

Когда резисторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общее полное сопротивление ряда резисторов, подключенных таким образом, вы складываете отдельные сопротивления. Это делается по следующей формуле: Rtotal = R1 + R2 + R3 и так далее.Пример: чтобы рассчитать общее сопротивление для этих трех последовательно соединенных резисторов.

Rtotal = R1 + R2 + R3 = 100 + 82 + 1 Ом = 183 Ом

---

Задача 1:

Рассчитайте общее сопротивление следующего последовательно включенного резистора.

	R Итого	= _______________
		= _______________

	R Итого	= _______________
		= _______________

	R Итого	= _______________
		= _______________

Параллельные резисторы

Когда резисторы подключаются друг к другу (бок о бок), это называется параллельным подключением.Это показано ниже.

Два параллельных резистора

Для расчета общего полного сопротивления двух резисторов, подключенных таким образом, вы можете использовать следующую формулу:

Пример: чтобы рассчитать полное сопротивление для этих двух резисторов, включенных параллельно.

---

Задача 2:

Рассчитайте общее сопротивление следующего резистора, включенного параллельно.

Три или более резистора, включенных параллельно

Для расчета общего общего сопротивления ряда из трех или более резисторов, подключенных таким образом, вы можете использовать следующую формулу: Пример: Чтобы рассчитать общее сопротивление для этих трех резисторов, подключенных параллельно

---

Задача 3:

Рассчитайте полное сопротивление следующего резистора, включенного параллельно.

---

ответов

Задача 1

1 = 1492 Ом 2 = 2242 Ом 3 = 4847 Ом

Задача 2

1 = 5 Ом 2 = 9,57 Ом 3 = 248,12 Ом

Задача 3

1 = 5,95 Ом 2 = 23,76 Ом Загрузите pdf-версию этой страницы здесь. Подробнее об авторе подробнее »

© Kitronik Ltd — Вы можете распечатать эту страницу и ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.

Формулы и калькулятор »Электроника

Формулы, расчеты и калькулятор для определения общего сопротивления резисторов, установленных последовательно и параллельно.

---

Resistance Tutorial:
Что такое сопротивление Закон Ома Омические и неомические проводники Удельное сопротивление Таблица удельного сопротивления для распространенных материалов Температурный коэффициент сопротивления Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов

---

Резисторы могут быть размещены во многих конфигурациях в электрической или электронной схеме — иногда последовательно, иногда параллельно.

Когда они размещаются в этих конфигурациях, важно иметь возможность рассчитать общее сопротивление.Этого можно довольно легко достичь, если использовать правильные формулы — есть простые формулы как для последовательных, так и для параллельных резисторов.

При проектировании электронной схемы или по какой-либо другой причине возможность вычисления сопротивления комбинации резисторов может быть очень полезной.

В электронных схемах комбинации резисторов могут быть сведены к последовательным элементам и параллельным элементам, хотя при использовании других электронных компонентов комбинации могут быть более сложными.Однако во многих случаях расчет значений последовательного и параллельного сопротивления имеет большое значение.

Резисторы серии

Самая простая конфигурация электронной схемы — это резисторы, включенные последовательно. Это может произойти, если несколько этих электронных компонентов соединены последовательно, или необходимо добавить сопротивление кабеля к сопротивлению резистора и т. Д.

Если резисторы соединены последовательно, то общее сопротивление является просто суммой отдельных резисторов.

Последовательные резисторы

Величину резисторов или сопротивлений, включенных последовательно, можно математически выразить следующим образом:

Пример расчета последовательных резисторов:
В качестве примера, если три резистора с номиналами 1 кОм, 2 кОм и 3 кОм соединены последовательно, то общее сопротивление составит 1 + 2 + 3 кОм = 6 кОм.

В реальных жизненных ситуациях и аспектах проектирования электрических и электронных схем будет много областей, где есть электронные компоненты, такие как резисторы или другие элементы, вносящие сопротивление, где необходимо суммировать ряд последовательно включенных сопротивлений.

Параллельно подключенные резисторы

Есть также много случаев, когда электронные компоненты, такие как резисторы, а также другие элементы, вызывающие сопротивление, появляются в электрической или электронной цепи параллельно.

Если резисторы размещены параллельно, они разделяют ток, и ситуацию немного сложнее вычислить, но все же довольно легко.

1Rtotal = 1R1 + 1R2 + 1R3 + ……

Пример расчета сопротивления резисторов, включенных параллельно:
Чтобы дать пример, если есть три резистора, подключенных параллельно со значениями 1 кОм, 2 кОм и Омега и 3 кОм, то можно вычислить общее значение комбинации:

1 / R Итого = 1/1000 + 1/2000 + 1/3000

1 / R Итого = 1/1000 + 1/2000 + 1/3000

1 / R Итого = 6/6000 + 3/6000 + 2/6000

1 / R Итого = 11/6000

R Всего = 6000/11 Ом или 545 Ом

Корпус только двух резисторов, включенных параллельно

Во многих конструкциях электронных схем наиболее распространенный экземпляр параллельных резисторов состоит только из двух электронных компонентов.

Часто бывает так, что один резистор подключается параллельно другому. Или другой случай может быть, когда резистор помещается на клеммы для цепи или сети, которая имеет определенное сопротивление. В этом случае необходимо только рассчитать общее сопротивление для двух параллельно включенных резисторов.

Если необходимо рассчитать общее значение для двух параллельных резисторов, уравнение можно изменить и значительно упростить, как показано ниже:

Эта формула значительно упрощает вычисление номинала двух параллельных резисторов, так как требует только одного умножения, одного сложения и одного деления.Часто это можно сделать мысленно или на клочке бумаги. В качестве альтернативы можно использовать наш простой калькулятор для двух параллельно включенных резисторов, приведенный ниже.

Калькулятор для двух резисторов, включенных параллельно

Этот калькулятор параллельного сопротивления обеспечивает простой метод расчета общего сопротивления для двух резисторов, соединенных параллельно.

Хотя параллельный расчет номиналов резисторов для двух резисторов упрощается до простой формулы, иногда гораздо проще и быстрее использовать калькулятор.

Чтобы использовать калькулятор параллельных резисторов, просто введите значения параллельных резисторов в Ом, Ом или кОм и т. Д. В два поля ввода, но обратите внимание, что все значения должны быть в одних и тех же единицах, то есть оба в Ом кОм МОм и т. Д. Затем вычислитель параллельных резисторов предоставит общее сопротивление двух резисторов в тех же единицах, что и вход.

Введите два значения для резисторов, R1 и R2, в поля, представленные в калькуляторе ниже, нажмите «Рассчитать», и будет предоставлено общее сопротивление.

Калькулятор параллельного сопротивления

Калькулятор параллельных резисторов обеспечивает простой способ рассчитать сопротивление двух резисторов, включенных параллельно, экономя записывать все и прибегая к ручке и бумаге или калькулятору в той или иной форме.

Знание того, как рассчитывать значения резисторов, включенных последовательно и параллельно, является ключом к пониманию того, как работают электрические и электронные схемы. Эти концепции используются как вторая натура при проектировании электрических и электронных схем.

Другие основные концепции электроники:
Напряжение Текущий Мощность Сопротивление Емкость Индуктивность Трансформеры Децибел, дБ Законы Кирхгофа Q, добротность Радиочастотный шум
Вернуться в меню «Основные понятия электроники». . .

Серия

и параллельные резисторы

• Изучив этот раздел, вы сможете:
• Рассчитайте значения общего сопротивления в цепях с последовательным сопротивлением.
• Используйте соответствующие формулы для расчета сопротивления в цепях с параллельным сопротивлением.
• • Вычисление суммы обратных величин.
• • Произведение над суммой.
• Рассчитайте значения общего сопротивления в последовательной / параллельной сети.

Расчеты в последовательно- и параллельных резисторных цепях

Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:

ПОСЛЕДОВАТЕЛЬНО, так что один и тот же ток течет через все компоненты, но на каждом из них может существовать разная разность потенциалов (напряжение).

ПАРАЛЛЕЛЬНО, так что одинаковая разность потенциалов (напряжение) существует на всех компонентах, но каждый компонент может проводить разный ток.

Рис. 4.2.1 Резисторы серии

Рис. 4.2.2 Параллельные резисторы

В любом случае (для резисторов) общее сопротивление той части цепи, которая содержит резисторы, может быть рассчитано с использованием методов, описанных ниже.

Возможность рассчитать суммарное (общее) значение резисторов таким способом позволяет легко вычислить неизвестные значения сопротивления, тока и напряжения для довольно сложных схем с использованием относительно простых методов.Это очень полезно при поиске неисправностей.

ПЕРЕД ДАЛЬНЕЙШЕЙ ДАЛЬНЕЙШЕЙ ПОПРАКТИКОЙ ИСПОЛЬЗУЙТЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ОБЩИХ ЗНАЧЕНИЙ СЕРИЙНЫХ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.

Для резисторов в серии:

Общее сопротивление двух или более резисторов, подключенных последовательно , определяется простым сложением индивидуальных значений резисторов, чтобы найти общую сумму (R _TOT ):

Для резисторов, включенных параллельно:

Для расчета общего сопротивления цепи, в которой используются параллельные резисторы, можно использовать следующую формулу.

Обратите внимание, однако, что эта формула НЕ дает вам общего сопротивления R _TOT . Это дает вам ВЗАИМОДЕЙСТВИЕ R _TOT или:

Это совсем другое значение — и НЕ является полным сопротивлением. Он делится на 1, разделенный на _TOT . Чтобы получить правильное значение для R _TOT (которое будет обратным 1/ _TOT , т. Е. _TOT /1, просто нажмите соответствующую клавишу на вашем калькуляторе (отмеченную 1 / x или x-1) .

Другой способ расчета параллельных цепей.

Суммарное сопротивление двух резисторов, включенных параллельно , которое не включает обратные, определяется как:

Эту формулу часто называют «произведение над суммой».

Он рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее сопротивление, как если бы это был один резистор, и составьте еще одну пару с третьим резистором.Определите новую сумму и так далее, пока вы не включите все параллельные резисторы в этой конкретной сети.

О, еще кое-что, что нужно помнить о произведении над суммой, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его для разделения продукта (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неправильным.

Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто встречаетесь с множеством параллельных сетей с гораздо более чем двумя резисторами.Тем не менее, какую формулу вы выберете, зависит от вас, взаимная или сумма продукта.

подсказок

Использование обратного метода

Если вы используете МЕТОД ВЗАИМОДЕЙСТВИЯ для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили обратные величины отдельных резисторов — вы должны снова найти обратную величину. 1 / R1 + 1 / R2 + 1 / R3 = 1 / R _TOT , и чтобы найти R _TOT , вы должны найти обратную величину 1 / R _TOT .

Упрощающие схемы

Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, по которой можно найти R _TOT .

Вы можете использовать формулу «произведение на сумму»:

Для цепей с более чем двумя параллельными резисторами просто определите два параллельных резистора одновременно, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резистора одним резистором, значение которого является объединенным сопротивлением двух .

Теперь вы можете использовать первое комбинированное значение в качестве единственного резистора со следующим параллельным резистором и так далее. Таким образом, можно выработать большое количество параллельных резисторов с использованием произведения на сумму.

Когда все параллельные резисторы одинакового номинала.

Если подключено несколько одинаковых параллельных резисторов, общее сопротивление будет равно номиналу резистора, умноженному на обратную величину количества резисторов.

, т. Е. Два параллельных резистора 12 кОм имеют общее сопротивление

.

12K x 1/2 = 6K

Три параллельно включенных резистора 12 кОм имеют суммарное сопротивление

12K x 1/3 = 4K и т. Д.

Проверяю ответ

Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.

Серия

и параллельная комбинация

Попробуйте несколько вычислений, основанных на последовательной и параллельной цепях резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят вычислить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать

Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».

Прежде чем начать, подумайте об этих нескольких советах. Они упростят задачу, если вы будете внимательно им следовать.

1. Разработайте ответы карандашом и бумагой; перерисуйте схему, над которой работаете.

2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу (например.грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.

3. Когда вы вводите значения в калькулятор, преобразуйте все значения KΩ или MΩ в Ом с помощью клавиши EXP. Если вы здесь ошибетесь, то получите действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.

Итак, вы прочитали эти инструкции, и вы готовы к работе. Вот способ решить типичную проблему на бумаге, чтобы (со временем) вы не запутались.

Пример последовательной и параллельной цепей

.

Хорошо, есть что вспомнить, так почему бы не попробовать несколько практических вопросов в Resistors Module 4.5 по определению полного сопротивления некоторых цепей резисторов?

Электрическое сопротивление в последовательных и параллельных сетях

Последовательное соединение

Общее сопротивление для резисторов, подключенных последовательно, можно рассчитать как

R = R ₁ + R ₂ + …. + R _n (1)

где

R = сопротивление (Ом, Ом)

Пример — Резисторы серии

Три резистора 33 Ом , 33 Ом и 47 Ом подключены последовательно. Общее сопротивление можно рассчитать как

R = ( 33 Ом) + ( 33 Ом) + ( 47 Ом)

= 113 Ом

Параллельное соединение

Общее сопротивление для резисторов, подключенных параллельно, можно рассчитать как

1 / R = 1 / R ₁ + 1 / R ₂ +…. + 1 / R _n (2)

Эквивалентное сопротивление двух параллельно соединенных резисторов можно выразить как

R = R ₁ R ₂ / (R ₁ + R ₂ ) ₍₃₎

Пример — параллельные резисторы

Три резистора 33 Ом , 33 Ом и 47 Ом подключены параллельно. Общее сопротивление можно рассчитать как

1 / R = 1 / ( 33 Ом ) + 1 / ( 33 Ом ) _{+ 1 / (47 Ом )}

= 0.082 (1 / Ом)

R = 1 / (0,082 Ом)

= 12,2 Ом

Если напряжение батареи составляет 12 В — ток в цепи можно рассчитать с помощью закон

I = U / R

= (12 В) / (12,2 Ом)

= 0,98 ампер

Можно рассчитать ток через каждый резистор

I ₁ = U / R ₁ = (12 В) / (33 Ом) = 0.