Делитель напряжения на резисторах. Расчет и принцип работы. | РОБОТИП
Так случается, что нам нужно получить напряжение другой величины, отличное от того, которое мы имеем. Для этой цели может подойти и другой источник питания, потенциометр, трансформатор и др.
Все зависит от того, как и где вы хотите использовать полученное напряжение.
В данной статье, я бы хотел рассказать о делите напряжения на резисторах. Это самый простой делитель напряжения из всех. Можно сказать, что классика среди делителей.
Во первых — делитель напряжения, это некое устройство (назовем его общим именем для того, чтобы дать понимание его предназначению), которое состоит из последовательно соединенных элементов, являющихся частью цепи, на выводах которых находится часть напряжения питания. Сумма напряжений на выводах каждого их элементов будет равняться общему напряжению равному источнику питания.
Начнем с самого начала:
Наглядно, как получается делить напряжение можно проследить на следующих рисунках:
Рис.1 — Источник питания с не замкнутой цепью.Рис.1 — Источник питания с не замкнутой цепью.
На рис.1 видно источник питания постоянного тока, и резистор. Цепь не замкнута, значит по ней не протекает ток.
Очень важно понимать, что ток протекает в замкнутой цепи. Иначе куда ему течь. Главной силой, которая движет наши заряды по проводникам в нашей схеме является источник питания. Благодаря ему создается в цепи напряжение и ток.
Так как резистор представляет собой цельный элемент (участок с определенным сопротивлением) без разрывов в цепи, то все приложенное напряжение с одного конца, будет равняться напряжению на другом его конце в виду того, что цепь не замкнута. Напряжение не заметит разницы, что на одном, что на другом конце резистора будет одно и тоже напряжение относительно минуса источника питания, для напряжения резистор просто проводник с неким сопротивлением — цепь же не замкнута, нагрузки для источника нет (зеленый цвет на рис. 1).
1).
Теперь давайте соединим нижний вывод резистора с минусом источника питания, получим следующую картину:
Рис.2 — замкнутая цепь с источником питания и резистором по которой протекает ток.Рис.2 — замкнутая цепь с источником питания и резистором по которой протекает ток.
Замкнув цепь с минусом источника питания, мы дали возможность току от источника питания, пройти через резистор и вернуться к источнику питания. Обратите внимание, что напряжение в цепи, помеченное зеленым цветом, уже не проходит через резистор напрямую, а сосредотачивается главным образом в верхней части. Через резистор уже идет ток (желтые точки).
Резистор, в нашей схеме, создал участок цепи с сопротивлением 10 кОм. Ток, который протекает в нашей цепи, можно рассчитать по закону Ома:
U = R x I
I = U / R
R = U / I
Подставив значения получим:
I = 10 В / 10 кОм = 0,001 А = 1 мА.
Немного пролили свет на то, что происходит в цепи с подключенным резистором.
Но, так как в схемах используют различные электронные компоненты, реализующие ту или иную логику работы, играясь с напряжениями и токами, то теперь давайте все же реализуем делитель на резисторах, как одного из «ведущих игроков» в этой отрасли.
Для этого последовательно добавим еще один резистор в нашу цепь :
Рис.3 — делитель напряжения на 2 резисторах с одинаковым номиналом.Рис.3 — делитель напряжения на 2 резисторах с одинаковым номиналом.
Мы подключили резистор с таким же номиналом сопротивления, как и предыдущий резистор.
Резистор подобрали одинаковый, для того, чтобы было проще и наглядней видеть, что происходит с напряжением и проследить зависимости.
Так как номиналы резисторов имеют одинаковое значение, то общее сопротивление цепи, состоящей из двух резисторов соединенных последовательно будет уже 20 кОм = 20000 Ом, так как при последовательном соединении резисторов сопротивление складываются.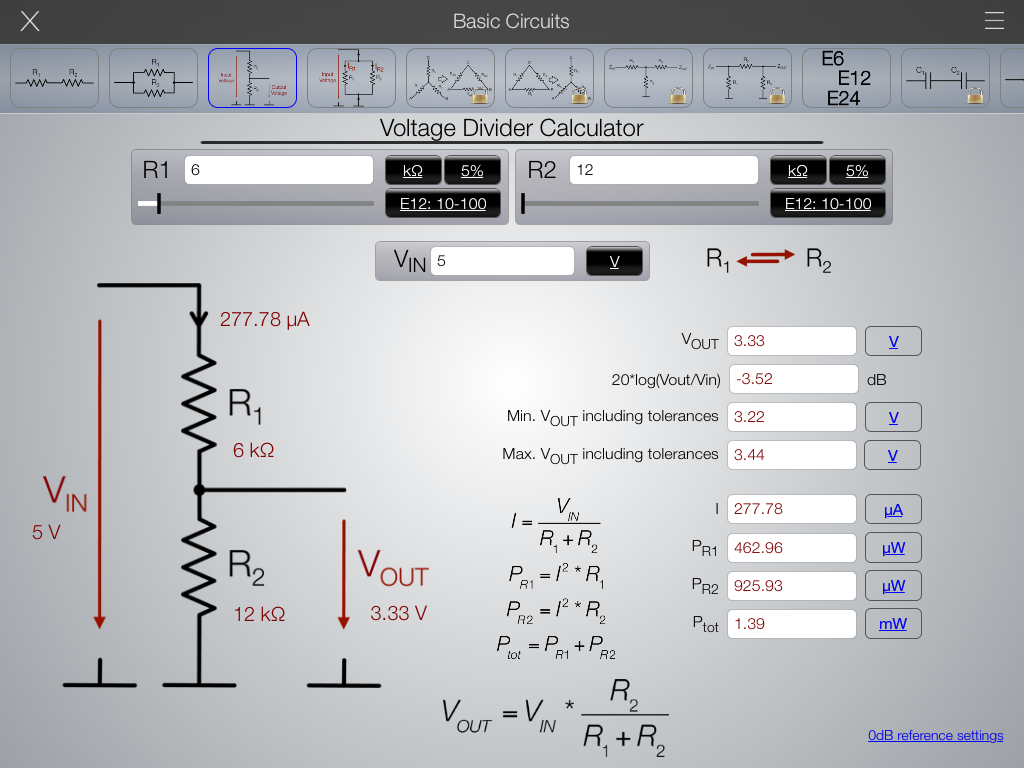 Сопротивление в 2 раза стало больше, значит ток, стал в два раза меньше, проверим это утверждение по формуле закона Ома:
Сопротивление в 2 раза стало больше, значит ток, стал в два раза меньше, проверим это утверждение по формуле закона Ома:
I = U / R = 10 / 20 = 0,0005 А или 0,5 мА (ток с одним был 1 мА) значит ток действительно стал в 2 раза меньше.
Для того, чтобы найти напряжение в точке соединения двух резисторов, нам нужно общий ток, который идет через оба резистора, по закону Ома умножить на сопротивление того элемента, напряжение на котором нам надо узнать.
Причем напряжение измеряется относительно минуса источника тока.
Для этого мы и рассчитали общий ток в цепи. Берем значение тока, умножаем на значение сопротивления и находим напряжение на выводах второго резистора:
U = R x I = 10 000 Ом x 0.0005А = 5В
Итог, в средней точке у нас напряжение равное 5 В.
Теперь давайте возьмем случай, когда используем разные номиналы резисторов:
Рис. 4 — делитель на резисторах с разным номиналом сопротивления
4 — делитель на резисторах с разным номиналом сопротивленияРис.4 — делитель на резисторах с разным номиналом сопротивления
В той же точке, где два резистора соединяются вместе мы будет иметь другое значение напряжения. В примере из рис.4, когда одно сопротивление равно 10 кОм, а второе 7 кОм мы получим напряжение равное примерно 4,12 В.
Рассчитывается значение напряжения точно так же, как и с 10 кОм выше.
На рис.4 случай с двумя резисторами, а теперь давайте усложним еще больше нашу схему и посмотрим, что будет если мы добавим резисторов в цепь:
Рис. 5 — делитель напряжения на примере разного числа резисторовРис. 5 — делитель напряжения на примере разного числа резисторов
На рис.5 можно видеть, как распределяется напряжение в разных ветвях цепи и на каждом элементе в отдельности. Все значения напряжения измеряются от минуса, следовательно занчения сопротивлений тоже считаются от минуса к плюсу.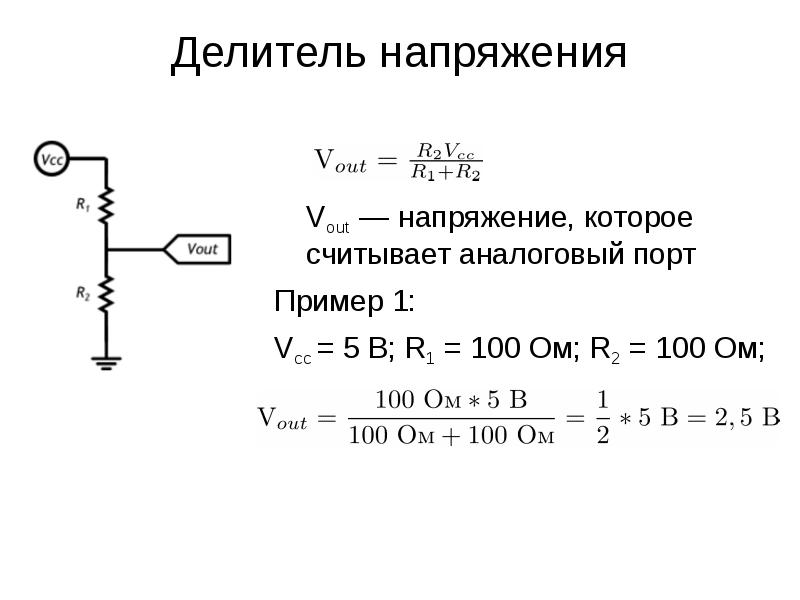
На рис.5 делитель состоящий из 4 резисторов по 1 кОм увеличивает свое сопротивление от нижнего к верхнему элементу, так как минус источника тока находится снизу.
Я упомянул слово «ветви» цепи, так как у нас уже 3 ветви и 2 узла. Но это уже совсем другая история, относящаяся к графам и затрагивающая очень обширную тему.
Важно понять суть происходящего, а она заключается в том, что у имея на руках источник питания постоянного тока, мы можем используя делитель напряжения на резисторах и получить нужную нам величину напряжения пользуясь лишь законом Ома.
Алгоритм очень прост
Для реализации делителя напряжения на сопротивлениях нужно сделать следующие шаги:
- Решить какое напряжение нам необходимо иметь на выходе;
- Задаться необходимым значением тока на выходе;
- Используя закон Ома найти необходимое значение сопротивлений для заданного тока;
Где и для чего используют делитель напряжения на резисторах описать в рамках той статьи сложно, да и нет необходимости, важно знать, что вся электроника переплетена делителями, как нитями.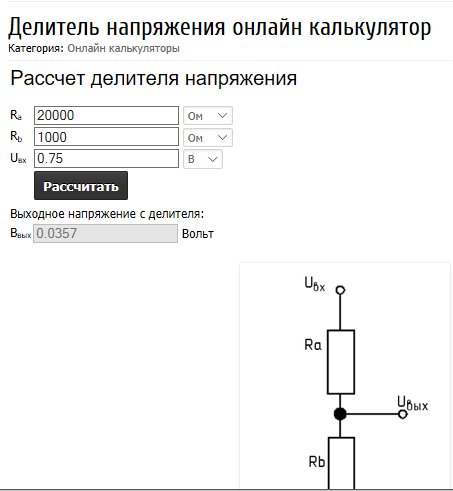
Спасибо, что дочитали до конца!
Подписывайте на канал РОБОТИП впереди много интересного!
напряжения на резисторе и после
При разработке печатных плат для электронного оборудования специалистам часто приходится выполнять расчет делителя. С виду простая схема помогает уменьшить выходное напряжение, необходимое для питания отдельных элементов цепи. Такая компоновка является базовой для электроники. В основу изучения принципа действия входят два момента: схематическое исполнение и формула для вычисления параметров работы делителя.
Что такое делитель напряжения
Схематическое исполнение понижающего устройства представляет собой последовательную цепь, состоящую из двух резистивных элементов. Суммарные значения сопротивлений позволяют уменьшить входящее напряжение до необходимых параметров на выходе. Между собой они связаны передаточным коэффициентом, находящимся в интервале от 0 до 1, включая границы (0<=aplha<=1).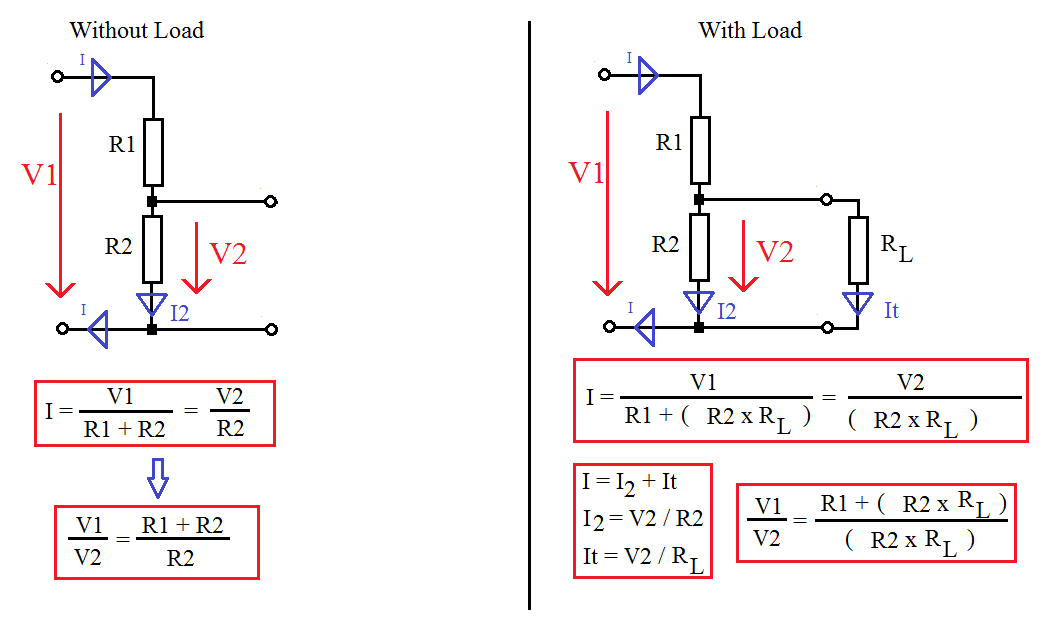
Существует несколько вариантов схематического исполнения приборов, но все они обладают одним и тем же функционалом — понижать вольтаж для потребителей, однако ток на всех полюсах остается одинаковым. Два последовательных участка цепи называют плечами. Нижнее плечо находится между центральной точкой и нулевым потенциалом. Именно здесь необходимо снимать показатели работы схемы. Другое плечо является верхним.
Простая схема на резисторах
В зависимости от расположения резисторов, различают линейные и нелинейные схемы делителей. Первый вариант используют для создания разности потенциалов и вольтажа в нескольких точках рабочих узлов. Понижение входного напряжения определяется по линейному закону.
Дополнительная информация! Понижающие узлы применяют для постоянного и переменного тока. Структурное исполнение обоих отличается друг от друга, поскольку в некоторых случаях требует включение дополнительных фильтров для подавления помех и шумов.
В нелинейных схемах разница определяется по передаточному коэффициенту. Такие устройства активно применяют в потенциометрах. Здесь учитывают присутствие активного и реактивного сопротивления, включая нелинейные и токовые нагрузки.
Принцип работы делителя напряжения
В состав простейшей понижающей схемы всегда входит не меньше одного резистора. Если элементы обладают одинаковыми коэффициентами сопротивляемости электронов, то на выходе вольтаж понизится в два раза. Для каждого узла понижение рассчитывается по закону Ома.
Внимание! Сумма пониженных величин в каждой точке равна общему вольтажу источника питания.
Схема с несколькими резисторамиРезисторы используют в принципиальных схемах с источником питания постоянного тока. В цепях переменного напряжения присутствует еще и реактивное сопротивление, куда входят конденсаторы, индуктивные катушки и другие элементы с электромагнитными полями.
В цепях с синусоидальным током в качестве резистивного элемента выступает конденсатор или катушка.
Кроме конденсаторов, в качестве реактивных компонентов также могут выступать индуктивные катушки, которые могут присутствовать в платах переменного тока. Коэффициент реактивного сопротивления обмоток также прямо пропорционален их номинальным значениям. Для вычислений также необходимо постоянное число ПИ, частота переменного магнитного поля (Гц) и индуктивность (Генри).
Делитель на индукционных катушкахВнимание! В описании выше токовая нагрузка равна бесконечности, поэтому все значения верны только при полученных показателях делителя на сопротивления нагрузки. Они в несколько раз больше внутреннего.
Формула для расчета делителя напряжения
Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:
- U — напряжение, В;
- I — ток, А;
В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно. В формуле использованы показатели:
График зависимости показателей от сопротивления- R — реактивное сопротивление;
- R — сопротивление, Ом.
- pi — постоянное число Пи, равное 3,14;
- f — частота, Гц;
- L — индуктивность катушки, Генри;
- C — емкость конденсатора, Фарад.
Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.
На резисторе
В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.
После резистора
Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:
- Uвых — вольтаж на выходе, В;
- Uпит — входной вольтаж, В;
- R1 — первый узел, Ом;
- R2 — второй узел, Ом.
Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).
Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.
Расчет делителя. Делитель напряжения
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.
Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
Вашему вниманию подборка материалов: Схема традиционного резисторного делителя напряженияДля применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. Расчет резистивного делителя напряжения[Напряжение на выходе, В ] = [Напряжение питания, В ] * / ( + [Сопротивление резистора R2, Ом ]) Из этой формулы, в частности, видно, что резисторные (резистивные) делители выдают стабильное выходное напряжение, если напряжение питания фиксировано. = [Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ] Эта формула верна для ненагруженного делителя. Если делитель работает на нагрузку, то [Входное сопротивление делителя, Ом ] = [Сопротивление резистора R1, Ом ] + 1 / (1 / [Сопротивление резистора R2, Ом [Эквивалентное выходное сопротивление делителя, Ом ] = 1 / (1 / [Сопротивление резистора R1, Ом ] + 1 / [Сопротивление резистора R2, Ом ]) = [Сопротивление резистора R2, Ом ] / ([Сопротивление резистора R1, Ом ] + [Сопротивление резистора R2, Ом ]) [Действующее / мгновенное / амплитудное напряжение на выходе делителя, В ] = [Коэффициент ослабления сигнала ] * [Действующее / мгновенное / амплитудное напряжение на входе делителя, В ] Эта формула верна, если ток нагрузки делителя равен нулю. Пример — делитель для осциллографаЕсли мы хотим получить осциллограмму высокого напряжения, то сразу приходит в голову делитель напряжения. Изготавливаем делитель, подключаем его вход к источнику высоковольтного сигнала, а выход к входу осциллографа. Должны получить на входе осциллографа уменьшенную копию входного сигнала. Если наш сигнал имеет достаточно большую частоту или просто резкие фронты (например, меандр), то ничего не получится. Осциллограмма не будет похожа на изначальный сигнал. Причина в том, что осциллограф имеет некоторую входную емкость, которая образует с эквивалентным выходным сопротивлением делителя фильтр нижних частот. Все высшие гармоники сигнала подавляются. Кроме того этот фильтр формирует фазовый сдвиг. Это бывает существенным для многолучевых осциллографов, когда мы анализируем соотношения сигналов. Чтобы этого избежать, резистор R1 нужно зашунтировать конденсатором. Качество усилителей звуковой частоты. Обзор, схемы…. Как не спутать плюс и минус? Защита от переполярности. Бесперебойник своими руками. ИБП, UPS сделать самому. Синус, синусоида… Применение тиристоров (динисторов, тринисторов, симисторов). Схемы. Ис… Соединение светодиодов. Последовательное, параллельное включение оптоэ… Параллельное, последовательное соединение резисторов. Расчет сопротивл… |
Как сделать делитель напряжения на резисторах? Часто в практике электронщика возникает необходимость снизить величину входного напряжения либо напряжение на отдельном участке цепи в строго определенной количество раз.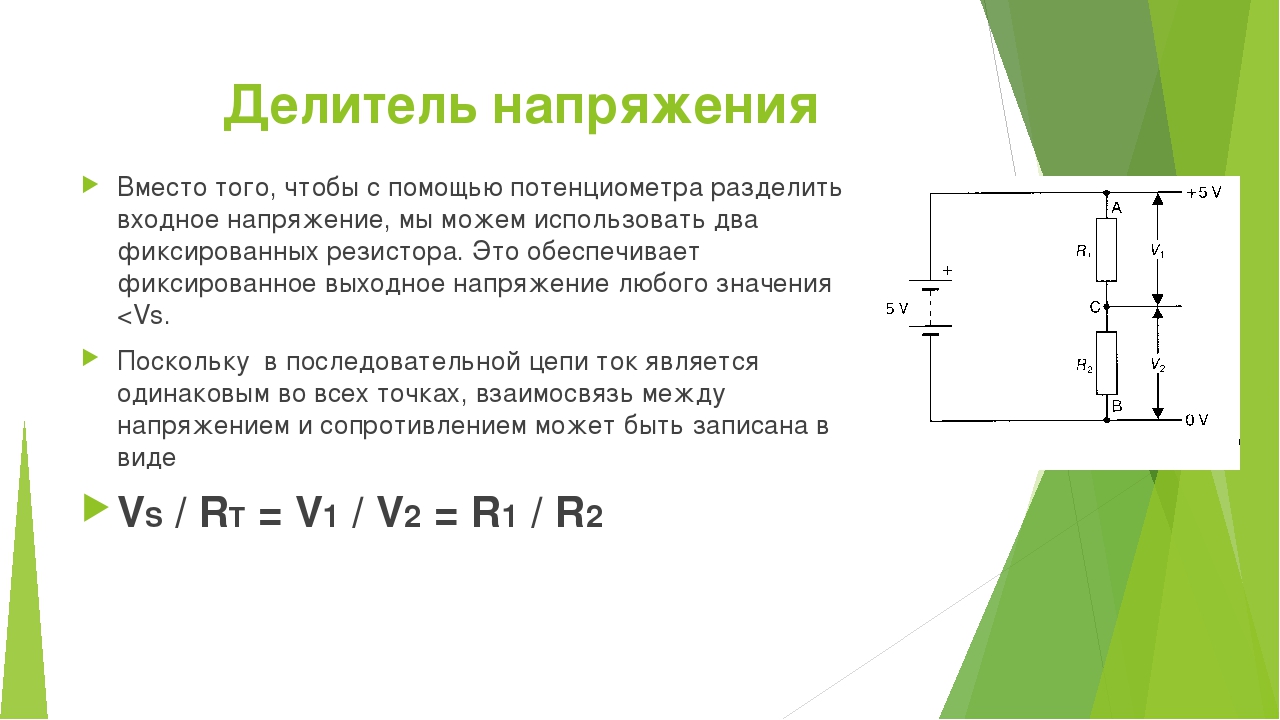 Например, величина входного напряжения 50 В , а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В (рис. 1 ). Для этого используются делители напряжения.
Например, величина входного напряжения 50 В , а выходное напряжение нужно получить в 10 раз меньше, т. е. 5 В (рис. 1 ). Для этого используются делители напряжения.
Рис. 1 — Структурная схема делителя напряжения
Они бывают разных типов и выполняются на безе , катушек индуктивности (рис. 2 ). Однако мы рассмотрим только наиболее применяемые на практике делители напряжения.
Рис. 2 — Элементы, применяемые в качестве делителей напряжения
Наиболее простым делителем напряжения являются два последовательно соединенных резистора R1 и R2 , которые подключены к источнику напряжения U (рис. 3 ). Если сопротивление резисторов одинаковы R1 = R2 , то напряжение источника питания разделится поровну на них U1 = U2 = U/2 .
Рис. 3 — Общая схема делителя напряжения на резисторах
Расчет делителя напряжения на резисторахДавайте разберемся как происходит деление напряжения. Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I , протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U и обратнопропорционален сопротивлению цепи (или ее участка) R , т. е.
Для этого нам понадобится знание только закона Ома, который, если говорить очень обобщенно, звучит так: ток I , протекающий в цепи (или на ее участке), прямопропорционален приложенному напряжению U и обратнопропорционален сопротивлению цепи (или ее участка) R , т. е.
откуда
Также следует знать, что в последовательной цепи, т. е. в цепи, в которой все резисторы соединены последовательно, ток I протекает одной и той же величины через все резисторы, а общее сопротивление последовательно соединенных резисторов равно сумме сопротивлений всех резисторов Rобщ = R1+R2 .
Теперь, на основании выше сказанного, давайте определим напряжения на резисторах в зависимости от величины их сопротивлений и напряжения источника питания.
Ток I , протекающий в цепи, равен отношению напряжения U к сумме сопротивлений R1+R2 , т. е.
Падение напряжения на первом резисторе равно
По аналогии находим падение напряжения на втором резисторе
Теперь в выражение (2) и (3) подставим значение тока из выражения (1), в результате получим
Делитель напряжения на резисторах. Различные номиналы резисторов
Различные номиналы резисторов С помощью полученных формул можно определить падение напряжения на резисторе, зная только величину входного напряжения и сопротивления самих резисторов. Однако такие формулы часто применимы лишь в теоретических расчётах. На практике же гораздо проще пользоваться основным свойством любого делителя напряжения, которое заключается в том, что при соответствующем подборе сопротивлений резисторов R1 и R2 выходное напряжение составляет часто входного (рис. 4 ).
Рис. 4 — Схемы делителей напряжения на резисторах
Следует обратить внимание на то, что величина выходного напряжения зависит от относительного значения сопротивлений резисторов R1 и R2 , а не от абсолютного.
Рис. 5 — Схемы делителей напряжения с одинаковым коэффициентом деления при разных номиналах резисторов
Здесь возникает вопрос: какие же номиналы резисторов R1 и R2 применять, 3 кОм и 1 кОм или 30 кОм и 10 кОм ? Все зависит от конкретного случая. Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1 и R2 , тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Однако есть рекомендация, которая исходит из закона Ома, чем меньше значение сопротивления R1 и R2 , тем больший ток будет протекать в цепи и тем большую мощность можно получить с выхода делителя напряжения, но нужно помнить, что эта мощность ограничивается мощностью источник питания и не может ее превысить.
Также делитель напряжения можно выполнять из нескольких последовательно соединенных резисторов (рис. 6 ).
Рис. 6 — Схема делителя напряжения с несколькими резисторами
И так, мы рассмотрели резисторный делитель напряжения с фиксированным значением выходного напряжения. Однако часто возникает необходимость в плавном изменении выходного напряжения. Например, при регулировании громкости звука мы плавно изменяем напряжение на усилителе.
Для плавного регулирования величины выходного напряжения применяются переменные и подстроечные резисторы (рис. 7 ).
Рис. 7 — Переменные и подстроечные резисторы
Переменный резистор еще называют потенциометром. Конструктивно он состоит из корпуса, имеющего три вывода, и рукоятки. При вращении ручки осуществляется скользящих контакт подвижной металлической пластины, которая замыкает две токопроводящие графитные дорожки, имеющие разную проводимость в зависимости от длины. Благодаря этому изменяется сопротивление межу двумя, рядом расположенными, выводами. А сопротивление между двумя крайними выводами остается всегда неизменным.
Схема подключения переменного резистора или же потенциометра приведена ниже (рис. 8 ). Два крайних вывода подключаются к источнику питания, а между средним и одним из крайних выводов снимается выходное напряжение, величину которого можно изменять от нуля до значения входного напряжения Uвых = 0…Uвх .
Рис. 8 — Схема включения переменного резистора для деления напряжения
Если, проворачивая ручку резистора, мы введем все сопротивление (как показано на схеме (рис. 9 )), то выходное напряжение будет равно входному Uвых = Uвх , так как подводимое напряжение будет полностью падать на сопротивлении резистора.
9 )), то выходное напряжение будет равно входному Uвых = Uвх , так как подводимое напряжение будет полностью падать на сопротивлении резистора.
Если же вывести все сопротивление, то выходное напряжение будет равно нулю Uвых = 0 .
Рис. 9 — Схема плавного изменения напряжения
Некоторые виды переменных резисторовВ зависимости от степени относительного изменения сопротивления при вращении рукоятки переменного резистора их разделяют на три типа (рис. 10 ):
1) с линейной зависимостью;
2) с логарифмической зависимостью;
3) с экспоненциальной зависимостью.
Рис. 10 — Зависимости переменных резисторов
Переменные резисторы с логарифмической зависимостью часто используются для регулировки уровня звука, поскольку ухо человека воспринимает звук именно по такой зависимости.
Кроме того переменные резисторы бывают как одинарные, так и сдвоенные. Последние находят широкое применение в звуковой технике.
Последние находят широкое применение в звуковой технике.
Делители напряжения на резисторах одинаково работают и рассчитываются как для постоянного, так и для переменного напряжения. Однако, в качестве делителей переменного напряжения также часто используются конденсаторы и реже – катушки индуктивности.
Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета.
Как работает делитель напряжения на резисторах
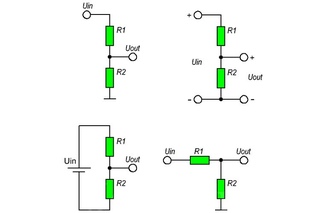
Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора.
Схема включает в себя входное напряжение и два резистора.
Резистор, находящийся ближе к плюсу входного напряжения Vвх , обозначен R1 , резистор находящийся ближе к минусу обозначен R2 . Падение напряжения Vвых — это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов.
Расчет делителя напряжения на резисторах основан на законе Ома .
V вых = R2 х V вых / R1 + R2
Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе . Смотрите калькулятор делителя напряжения на резисторах онлайн.
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель
напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов .
Это схема, строящаяся на основе пары резисторов .
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе V out ? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1 и R2 одинаков пока к выходу V out ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2 , расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество
компонентов, которые меняют своё сопротивление в зависимости от внешних условий.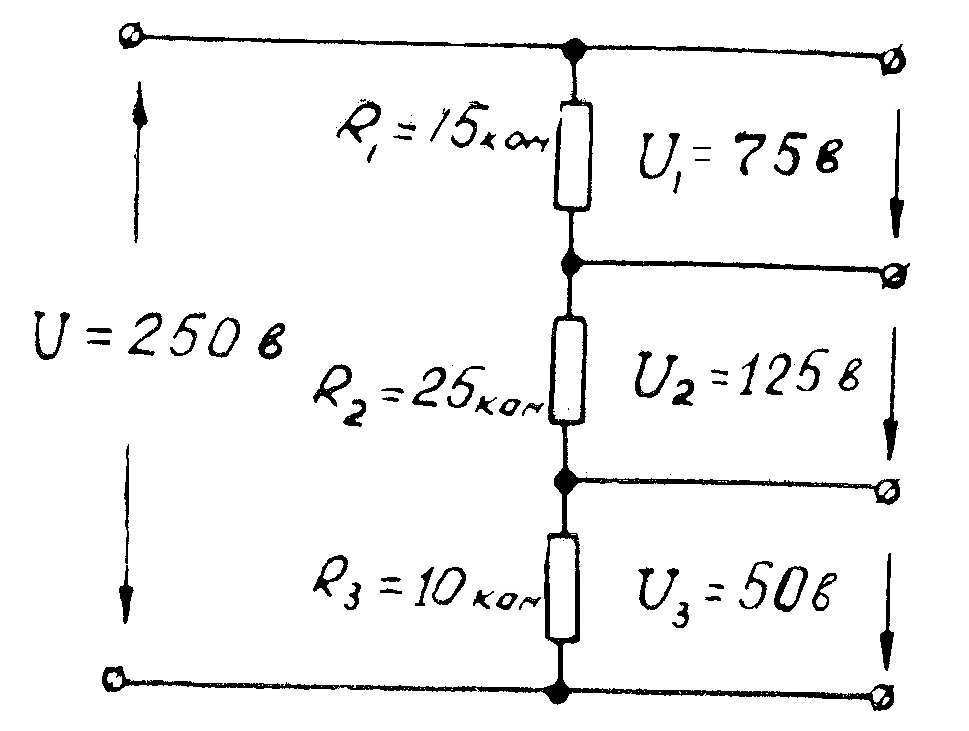 Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Так термисторы меняют сопротивление от нуля до определённого значения в зависимости
от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего
на них света и т.д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, V out будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию на переменный компонент и общую формулу расчёта V out .
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
В этом случае V out уже не может быть расчитано лишь на основе значений V in , R1 и R2 : сама нагрузка провоцирует дополнительное падение напряжения
(voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда
её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта V out , получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки. И тем ощутимее будут потери, чем больше номинал R2 по отношению к сопротивлению L . Чтобы нивелировать этот эффект мы могли бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших номиналов.
Пропорция сохраняется, V out не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от
источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если
устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка
на сами резисторы.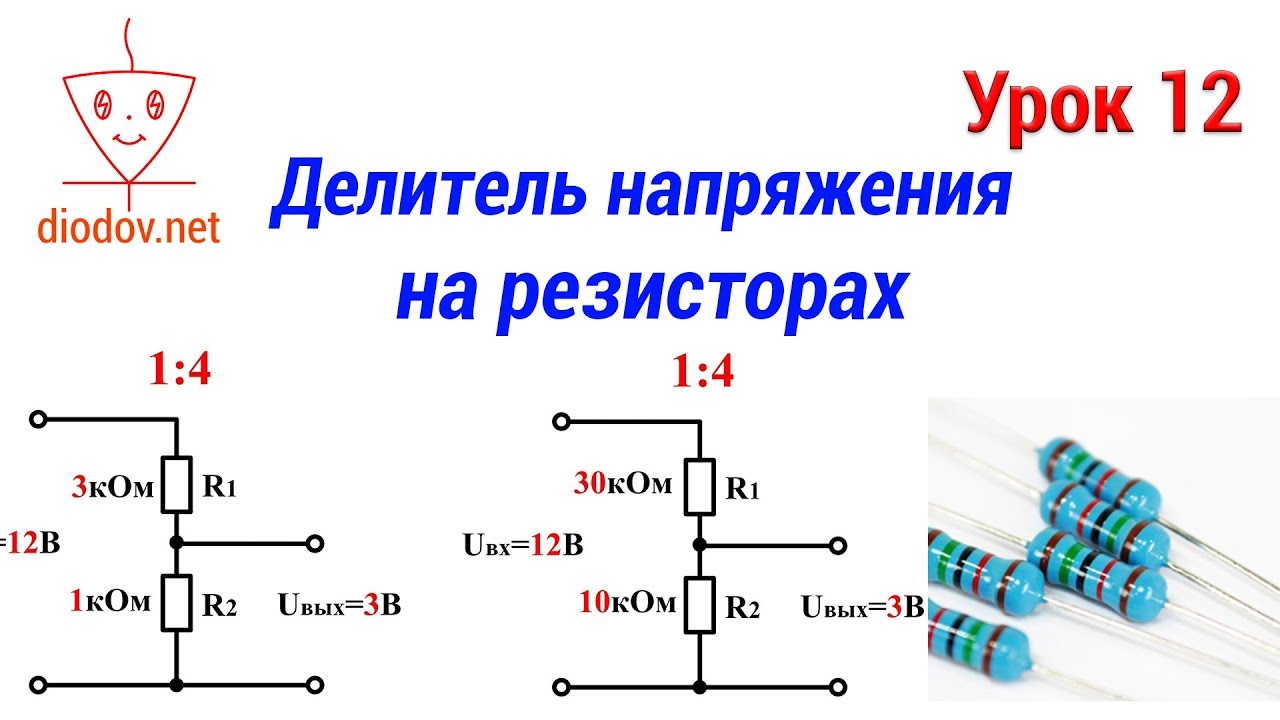 Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое
самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out также будет неравномерным.
Калькулятор делителя напряженияДелитель напряжения представляет собой схему, которая делит более высокие напряжения на более низкие с помощью пары резисторов. Это может быть сложной задачей для новичков, которые еще не понимают всех основ или того, как использовать формулу делителя напряжения. Вот почему мы создали этот удобный калькулятор делителя напряжения, который вы можете использовать для расчета сопротивления, необходимого для ваших цепей делителя напряжения. Все, что вам нужно сделать, это ввести любые три из приведенных ниже значений, и недостающее будет рассчитано автоматически.Это не может быть проще!
Калькулятор делителя напряжения
Наш калькулятор делителя напряжения работает по стандартной формуле делителя напряжения: Vout = (Vin x R2) / (R1 + R2)
Давайте немного разберем это, чтобы было проще понять:
- Vin это входное напряжение вашего блока питания или аккумулятора
- R1 сопротивление 1-го резистора в Омах
- R2 сопротивление 2-го резистора в Омах
- Vout — выходное напряжение с делителя напряжения
На этом схематическом изображении видно, что при использовании двух резисторов (R1=4. 7 кОм, R2 = 6,8 кОм), что мы можем создать выход 5 вольт из 12 вольт. Этот делитель напряжения преобразует 12 вольт в 5 вольт:
7 кОм, R2 = 6,8 кОм), что мы можем создать выход 5 вольт из 12 вольт. Этот делитель напряжения преобразует 12 вольт в 5 вольт:
Вы можете использовать приведенный выше калькулятор делителя напряжения для быстрого вычисления любого из этих значений. Мы также составили таблицу наиболее распространенных делителей напряжения, из которых вы можете выбрать:
.| Комбинация резисторов | Использование |
| 4,7 кОм и 6,8 кОм | от 12 В до 5 В |
| 4.7 кОм и 3,9 кОм | от 9 В до 5 В |
| 3,6 кОм и 9,1 кОм | от 12 В до 3,3 В |
| 3,3 кОм и 5,7 кОм | от 9 В до 3,3 В |
Попробуйте ввести эти значения в калькулятор делителя напряжения, чтобы увидеть, как работают выходы! Это отличный способ познакомиться с ним (это поможет вам понять формулу делителя напряжения).
Рекомендации по делителю напряжения
При использовании калькулятора делителя напряжения и формулы следует помнить о нескольких вещах.Ни формула, ни калькулятор не подберут для вас компоненты и не отрегулируют это напряжение!
- Регулировка напряжения : Делители напряжения не регулируют напряжение. Если входное напряжение нестабильно и колеблется, то же самое будет и с выходами! Если вам нужен надежный источник питания, вы можете рассмотреть возможность добавления стабилизатора напряжения в вашу схему.
- Подходящий размер : Убедитесь, что резисторы правильно подобраны для нагрузки, которую вы планируете использовать в этой цепи.Большинство резисторов рассчитаны только на 1/4 или 1/2 Вт! Что-то, о чем многие забывают. Вам понадобятся резисторы большего размера для больших нагрузок. Возможно, вы захотите ознакомиться с нашим руководством по резисторам. И давайте будем честными, вы не должны использовать делитель напряжения для питания больших нагрузок.
 Это не эффективно, и есть лучшие варианты!
Это не эффективно, и есть лучшие варианты! - Потенциометры : Не забывайте о потенциометрах при сборке делителя напряжения. С помощью потенциометра вы можете отрегулировать сопротивление и настроить делитель напряжения.Это может быть особенно удобно при создании прототипа чего-либо, когда точное направление дизайна еще не определено.
Калькулятор делителя напряжения • Информатика и машинное обучение
Делитель напряжения позволяет преобразовывать входное напряжение в более низкое выходное напряжение. Например, вход 5 В можно довольно легко преобразовать в выход 3 В 3. Базовая установка состоит из двух резисторов:
Но выбрать правильные резисторы довольно сложно.Вы можете взять формулу и попробовать некоторые значения, чтобы аппроксимировать значения или использовать формулу калькулятора:
Возможные значения резисторов для входного напряжения 5 В и выходного напряжения 3,3 В, упорядоченные по ошибке:| R1 | R2 | Фактический | Ошибка | 6800V | 0,066V | 0,025 В | 0,066V | 0,066V | 0,066V | 0,066V | 0,066V | 0,025 Вт | 0,025 | 47Ω | 100Ω | 3. 401V 401V | 0.101V 0.170W | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 47kΩ | 100 кОм 3.401V | 0.101V 0.000W | ||||||||||||||||
| 4.7kΩ 10кОм | 3.401V 0.101V | 0.002W | ||||||||||||||||
| 470Ω 1кОм | 3.401V 0.101V | |||||||||||||||||
| 4.7Ω 10Ω | 3.401V 0.101V | |||||||||||||||||
| 220Ω 470Ω | 3.406V | 0.106V 0.036W | ||||||||||||||||
| 22кВт 47kΩ | 3.406V 0.106V | |||||||||||||||||
| 2,2 кОм 4.7kΩ | 3.406V 0.106V | 0,004 Вт | ||||||||||||||||
| 10 кОм 22 кОм | 3.438V 0.138V | |||||||||||||||||
| 100Ω 220Ω | 3.438V 0.138V | |||||||||||||||||
| 1кОм 2.2кОм | 3.438V 0.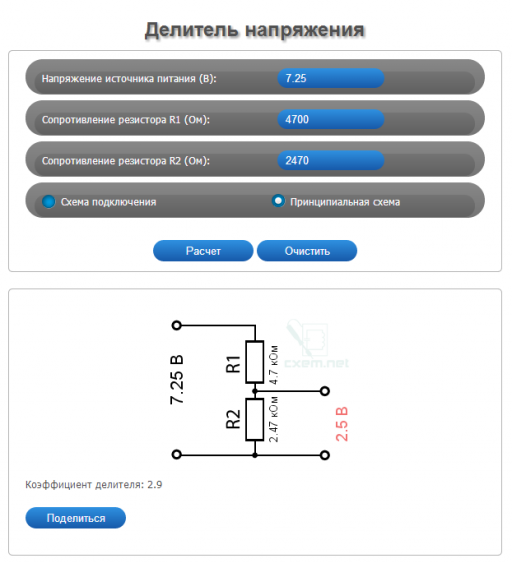 138V 138V | |||||||||||||||||
| 220Ω 330Ω | 3.000V 0.300V | |||||||||||||||||
| 2,2 кОм 3.3kΩ | 3.000V 0.300 В | 0,005 Вт |
Обратите внимание: не используйте делитель напряжения для высоких напряжений, так как весь ток должен проходить через резисторы, что сильно их повредит. Альтернативой являются регуляторы напряжения! И что еще более важно: В реальных делителях напряжения не следует использовать резисторы с низким сопротивлением.В столбце рассеиваемой мощности указано, сколько энергии преобразуется в тепло, и она должна быть как можно меньше.
Калькулятор делителя напряжения
Калькулятор делителя напряжения
Он используется для расчета падения напряжения на отдельной резисторной нагрузке при последовательном подключении. Он имеет четыре текстовых поля, в которые необходимо ввести общее напряжение, сопротивление первой, второй и третьей нагрузки. Первый и второй заряды необходимы, а третье сопротивление нагрузки обычно необязательно.После того, как все эти значения будут введены в соответствующие поля, вы можете нажать кнопку «Рассчитать», чтобы получить падение напряжения нагрузок в последовательности.
Первый и второй заряды необходимы, а третье сопротивление нагрузки обычно необязательно.После того, как все эти значения будут введены в соответствующие поля, вы можете нажать кнопку «Рассчитать», чтобы получить падение напряжения нагрузок в последовательности.Существует два типа правила делителя напряжения, которые включают цепь постоянного тока (DC) и цепь переменного тока (AC).
Делитель напряжения цепи постоянного тока Правило
Vi = VT Ri________Р1 + Р2 + Р3 + …
Где;
• Vi — падение напряжения в вольтах, а VT — падение напряжения или эквивалент источника напряжения в вольтах
• Ri — сопротивление резистора в омах (Ом)
• R1 — сопротивление резистора R1 в омах (Ом)
• R2 — сопротивление резистора R2 в омах (Ом)
• R3 — сопротивление резистора R3 в омах (Ом)
Например;
Источник напряжения ТН 20 В.Он подключен к резисторам R1 и R2 последовательно с сопротивлением 40 (Ом) и 50 (Ом) соответственно. Какое падение напряжения на резисторе R2?
Какое падение напряжения на резисторе R2?Растворы;
V2 = VT х R2 / (R1 + R2)= 20 В x 50 Ом / (40 Ом + 50 Ом) = 11,11 Вольт (В)
Цепь переменного тока Делитель напряжения Правило
Цепь переменного тока с последовательными нагрузками и источником напряжения, формула нагрузки и падения напряжения будет дана по формуле; Ви = ВТ Зи____
Z1 + Z2 + Z3 …
Где;
• Vi — падение напряжения в вольтах (В) и нагрузка Zi
• VT — падение напряжения в вольтах или эквивалентный источник напряжения
• Zi — полное сопротивление нагрузки Zi в омах (Ом)
• Z1 — полное сопротивление нагрузка Z1 в омах (Ом)
• Z2 — полное сопротивление нагрузки Z2 в омах (Ом)
• Z3 — полное сопротивление нагрузки Z3 в омах (Ом)
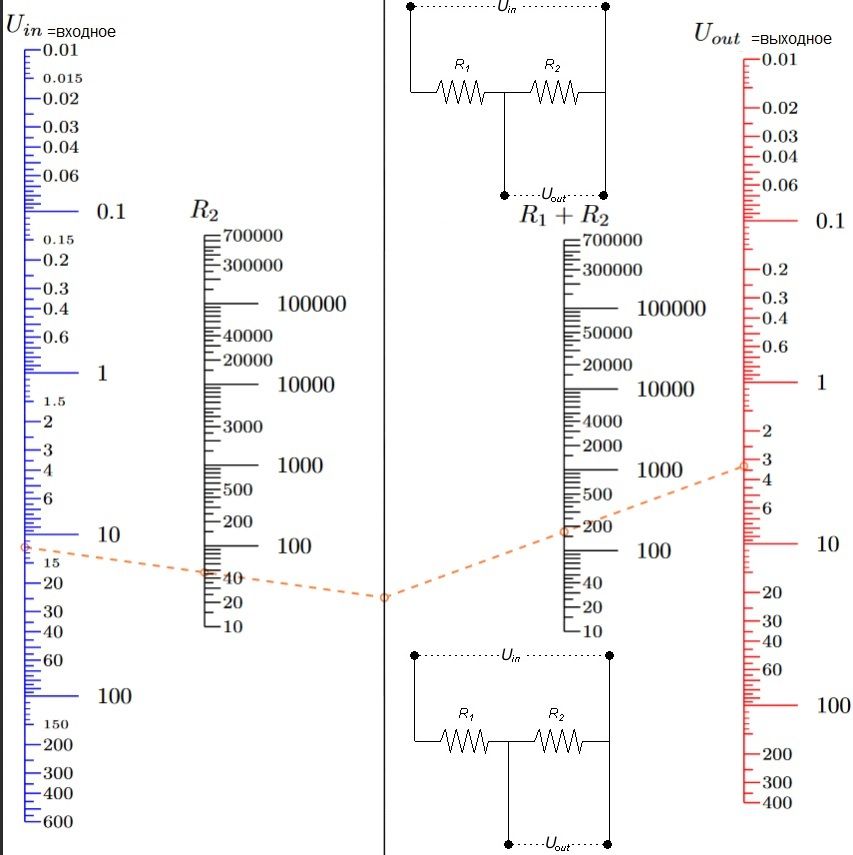
Окончательный мастер расчета делителя напряжения
Мастер позволяет рассчитать оптимальную пару стандартных последовательных резисторов для построения резистивного делителя напряжения.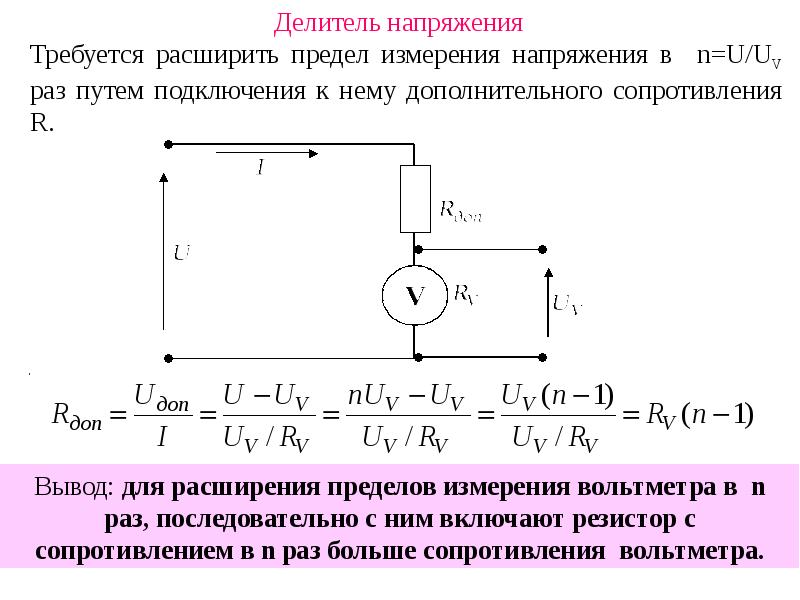
Можно либо ввести значения входного и выходного напряжения, либо напрямую ввести коэффициент усиления (< 1) делителя напряжения.
В таблице результатов показана лучшая пара резисторов, а также альтернативные решения, отсортированные в порядке возрастания ошибки.
На изображениях справа показаны фактические цветовые полосы или код маркировки SMD, присутствующие на реальных резисторах для выбранного решения.
В настоящее время отображается пример (выходное напряжение 3 В и серия E12).
Введите собственные значения в поля ниже и нажмите кнопку вычисления.
Серия резисторов E6E12E24E48E96E192Диапазон R1+R2 от 1 Ом до 10 Ом от 10 Ом до 100 Ом от 100 Ом до 1 кОм от 1 кОм до 10 кОм от 10 кОм до 100 кОм от 100 кОм до 1 МОм от 1 МОм до 10 МОм от 10 МОм до 100 МОм
2.02899
8,2 кОм
5,6 кОм
32,37%
2.02970
12 кОм
8,2 кОм
32,34%
2. 04348
04348
6,8 кОм
4,7 кОм
31,88%
2.04545
39 кОм
27 кОм
31,82%
2.05263
56 кОм
39 кОм
31,58%
2.06250
47 кОм
33 кОм
31,25%
2.22222
15 кОм
12 кОм
25,93%
2.24490
27 кОм
22 кОм
25,17%
2.25000
22 кОм
18 кОм
25%
2,25000
33 кОм
27 кОм
25%
2.25275
10 кОм
8,2 кОм
24,91%
2.25806
6,8 кОм
5,6 кОм
24,73%
2,26667
8,2 кОм
6,8 кОм
24,44%
2,26744
47 кОм
39 кОм
24,42%
2.27273
12 кОм
10 кОм
24,24%
2.27273
18 кОм
15 кОм
24,24%
2.28155
5,6 кОм
4,7 кОм
23,95%
2. 29167
29167
39 кОм
33 кОм
23,61%
2,50000
10 кОм
10 кОм
16,67%
2,50000
12 кОм
12 кОм
16,67%
2.50000
15 кОм
15 кОм
16,67%
2,50000
18 кОм
18 кОм
16,67%
2,50000
22 кОм
22 кОм
16,67%
2,50000
27 кОм
27 кОм
16,67%
2,50000
33 кОм
33 кОм
16,67%
2,50000
39 кОм
39 кОм
16,67%
2.50000
47 кОм
47 кОм
16,67%
2,50000
5,6 кОм
5,6 кОм
16,67%
2,50000
6,8 кОм
6,8 кОм
16,67%
2,50000
8,2 кОм
8,2 кОм
16,67%
2.70833
33 кОм
39 кОм
9,72%
2,71845
4,7 кОм
5,6 кОм
9,39%
2. 72727
72727
10 кОм
12 кОм
9,09%
2,72727
15 кОм
18 кОм
9,09%
2,73256
39 кОм
47 кОм
8,91%
2,73333
6,8 кОм
8,2 кОм
8,89%
2.74194
5,6 кОм
6,8 кОм
8,6%
2,74725
8,2 кОм
10 кОм
8,42%
2.75000
18 кОм
22 кОм
8,33%
2,75000
27 кОм
33 кОм
8,33%
2,75510
22 кОм
27 кОм
8,16%
2,77778
12 кОм
15 кОм
7,41%
2,93750
33 кОм
47 кОм
2,08%
2,94737
39 кОм
56 кОм
1,75%
2.95455
27 кОм
39 кОм
1,52%
2,95652
4,7 кОм
6,8 кОм
1,45%
2.97030
8,2 кОм
12 кОм
0,99%
2. 97101
97101
5,6 кОм
8,2 кОм
0,97%
2,97297
15 кОм
22 кОм
0,9%
2,97619
6,8 кОм
10 кОм
0,79%
3.00000
10 кОм
15 кОм
0%
3.00000
12 кОм
18 кОм
0%
3.00000
18 кОм
27 кОм
0%
3.00000
22 кОм
33 кОм
0%
3.14607
33 кОм
56 кОм
4,87%
3.17568
27 кОм
47 кОм
5,86%
3.17757
3.9 кОм
6,8 кОм
5,92%
3.17829
4,7 кОм
8,2 кОм
5,94%
3.19149
6,8 кОм
12 кОм
6,38%
3.19672
22 кОм
39 кОм
6,56%
3.20513
5,6 кОм
10 кОм
6,84%
3.21429
10 кОм
18 кОм
7,14%
3. 21429
21429
15 кОм
27 кОм
7.14%
3.23276
8,2 кОм
15 кОм
7,76%
3.23529
12 кОм
22 кОм
7,84%
3.23529
18 кОм
33 кОм
7,84%
3,36634
3,3 кОм
6,8 кОм
12,21%
3.37349
27 кОм
56 кОм
12,45%
3.38843
3,9 кОм
8,2 кОм
12.95%
3.40136
4,7 кОм
10 кОм
13,38%
3.40580
22 кОм
47 кОм
13,53%
3.40909
5,6 кОм
12 кОм
13,64%
3.42105
18 кОм
39 кОм
14,04%
3.43511
8,2 кОм
18 кОм
14,5%
3.43750
10 кОм
22 кОм
14.58%
3.43750
15 кОм
33 кОм
14,58%
3.44037
6,8 кОм
15 кОм
14,68%
3. 46154
46154
12 кОм
27 кОм
15,38%
3,56522
3,3 кОм
8,2 кОм
18,84%
3,57895
27 кОм
68 кОм
19,3%
3,58974
22 кОм
56 кОм
19.66%
3,59281
4,7 кОм
12 кОм
19,76%
3,59712
3,9 кОм
10 кОм
19,9%
3.61111
15 кОм
39 кОм
20,37%
3,61538
18 кОм
47 кОм
20,51%
3.62903
6,8 кОм
18 кОм
20,97%
3.64078
5,6 кОм
15 кОм
21.36%
3,64238
8,2 кОм
22 кОм
21,41%
3,64865
10 кОм
27 кОм
21,62%
3,66667
12 кОм
33 кОм
22,22%
3.75940
3,3 кОм
10 кОм
25,31%
3,76147
2,7 кОм
8,2 кОм
25,38%
3,77358
3,9 кОм
12 кОм
25. 79%
79%
3,77778
22 кОм
68 кОм
25,93%
3.78378
18 кОм
56 кОм
26,13%
3.79032
15 кОм
47 кОм
26,34%
3.80711
4,7 кОм
15 кОм
26,9%
3,81356
5,6 кОм
18 кОм
27,12%
3.81944
6,8 кОм
22 кОм
27.31%
3.82353
12 кОм
39 кОм
27,45%
Калькулятор делителя напряжения
- Дома
- Калькулятор делителя напряжения
Делитель напряжения на два резистора
является одной из самых основных и распространенных схем в электронике. Часто это первая схема, которую изучает новичок.
Делитель напряжения превращает большое напряжение в меньшее.Как это работает, соотношение резисторов (R1 и R2) делит вход
напряжение до более низкого выходного напряжения. Выходное напряжение представляет собой долю входного напряжения, и эта доля равна R2, деленному на
сумма R1 + R2. Формула имеет вид VВЫХ = VIN * (R2 / (R1 + R2)).
Калькулятор делителя напряжения предполагает, что вы знаете любые три значения схемы делителя напряжения.
Используйте калькулятор ниже, чтобы вычислить значение отсутствующего параметра.
Выходное напряжение представляет собой долю входного напряжения, и эта доля равна R2, деленному на
сумма R1 + R2. Формула имеет вид VВЫХ = VIN * (R2 / (R1 + R2)).
Калькулятор делителя напряжения предполагает, что вы знаете любые три значения схемы делителя напряжения.
Используйте калькулятор ниже, чтобы вычислить значение отсутствующего параметра.
Делители напряжения обычно используются для уменьшения входного напряжения на канал АЦП.Например, если вы хотите прочитать напряжение источника питания на 12 вольт, но ваш АЦП имеет максимальный входной уровень 5 вольт, делитель напряжения уменьшит напряжение до безопасный уровень.
Многие датчики являются резистивными, и АЦП не может получить от них правильные показания. Добавляя резистор к резистивному датчику, вы создаете делитель напряжения. Когда выход делителя напряжения известен, Вы можете рассчитать сопротивление датчика.
Используя делитель напряжения в сочетании с АЦП, можно считывать показания всех видов датчиков.
- тримпоты
- слайдеры
- батареи
- термисторы
- джойстики
- многое другое
Схемы делителя напряжения не подходят для понижения напряжения для использования в качестве источника питания.Мало того, что это было бы ужасно неэффективно, достаточный ток, протекающий через R1, может привести к сгоранию резистора. Как правило, никогда не используйте делитель напряжения. в качестве источника напряжения для всего, что требует даже скромного количества энергии. Если вам нужно понизить напряжение, чтобы использовать его в качестве источника питания, обратите внимание на стабилизаторы напряжения или импульсные источники питания.
Также обязательно ознакомьтесь с нашим Инструментом преобразования конденсаторов мкФ в нФ в пФ, который поможет вам выбрать правильные конденсаторы для вашего следующего проекта.
Калькулятор делителя напряжения и формулы для резисторного делителя напряжения
Формула делителя напряжения — это основная формула, которую вы должны выучить. С помощью этой формулы вы сможете создать множество проектов. В этой статье будет объяснено, как происходит резисторный делитель напряжения, а также формула и калькулятор делителя напряжения.
С помощью этой формулы вы сможете создать множество проектов. В этой статье будет объяснено, как происходит резисторный делитель напряжения, а также формула и калькулятор делителя напряжения.
| Рис. 1. Калькулятор делителя напряжения (слева) и схема делителя напряжения (справа)Вы узнаете, что такое делитель напряжения и почему он так важен в последовательных цепях. Чтобы понять основы последовательной схемы среднего делителя резистора, вы можете посмотреть на следующее изображение схемы делителя напряжения, где два резистора соединены последовательно. На приведенном выше изображении двух последовательно соединенных резисторов падение напряжения или падение напряжения на каждом резисторе (R1 и R2). 2 Положение этого падения напряжения обозначено V1 и V2 или обычно обозначено Vout1 и Vout2. , так как через каждый резистор проходит одинаковый ток, падение напряжения пропорционально значению сопротивления. Например, если значение резистора делителя R2 в два раза больше, чем R1, то значение V2 будет вдвое больше, чем V1. С помощью некоторых расчетов можно определить формулу, по которой напряжение делится между последовательно изготовленными резисторами. Обозначим падение напряжения на каждом резисторе Vx, где x представляет номер конкретного резистора. По закону Ома падение напряжения на каждом резисторе можно записать следующим образом: схема. Также по закону Ома ток равен напряжению источника, деленному на общее сопротивление. Тогда уравнение: I = Vs / Rtotal Тогда, подставив Vs / Rt вместо I в выражение Vxi.Rx, получим: Vx = (Vs * Rx) / Rtotal Принцип работы делителя напряжения заключается в следующем. падение напряжения на резисторе или комбинации резисторов в последовательной цепи равно отношению значения его сопротивления к общему сопротивлению, умноженному на напряжение источника. A. Примеры проблем и решений Ниже приведен пример и решение для деления напряжения резистора с помощью двух последовательных резисторов. Если вы не понимаете формулу закона Ома, вы можете прочитать статью здесь. Также есть калькулятор закона Ома. 1. Первый пример Если вы знаете Vs, R1 и R2, как найти Vout1 и Vout2? Ответ: Сначала найдите ток I, потому что токи в последовательном резисторе одинаковы.Формула I = Vs/(R1 + R2) Второй поиск для Vout1. Формула Vout1 = I.R1 В-третьих, ищите Vout2. Формула Vout2 = I.R2 2. Второй пример Если Vs, Vout1 и Vout2 известны, как найти R1 и R2? Ответ : Поскольку R1 и R2 неизвестны, единственным способом является определение Rtotal. Например, определяем, что сумма равна 2К Ом. Сначала найдите ток I.I = Vs / 2K Во-вторых, найдите сопротивление R1, формула R1 = (Vs- Vout1) / I В-третьих, найдите сопротивление R2, формула R2 = (Vs — Vout2) / I B. Калькулятор резистивного делителя напряжения Калькулятор резистивного делителя напряженияДля ускорения вычислений я сделал простой калькулятор делителя напряжения с двумя последовательно соединенными резисторами. С помощью этого калькулятора вы можете получить значение выходного напряжения, используемого сопротивления или общего напряжения. Не стесняйтесь экспериментировать со следующими калькуляторами: ВЫЧИСЛИТЕЛЬ ДЕЛИТЕЛЯ НАПРЯЖЕНИЯНадеемся, что эта статья о резисторном делителе напряжения вместе с формулой и объяснением поможет пандам понять, как устроена схема резисторного делителя напряжения. Благодарим вас за посещение веб-сайта Piko Chip. Может быть полезно. Источник: Electronics Fundamentals, FLOYD .  |
 С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы. Описание…
Описание…  Это не эффективно, и есть лучшие варианты!
Это не эффективно, и есть лучшие варианты!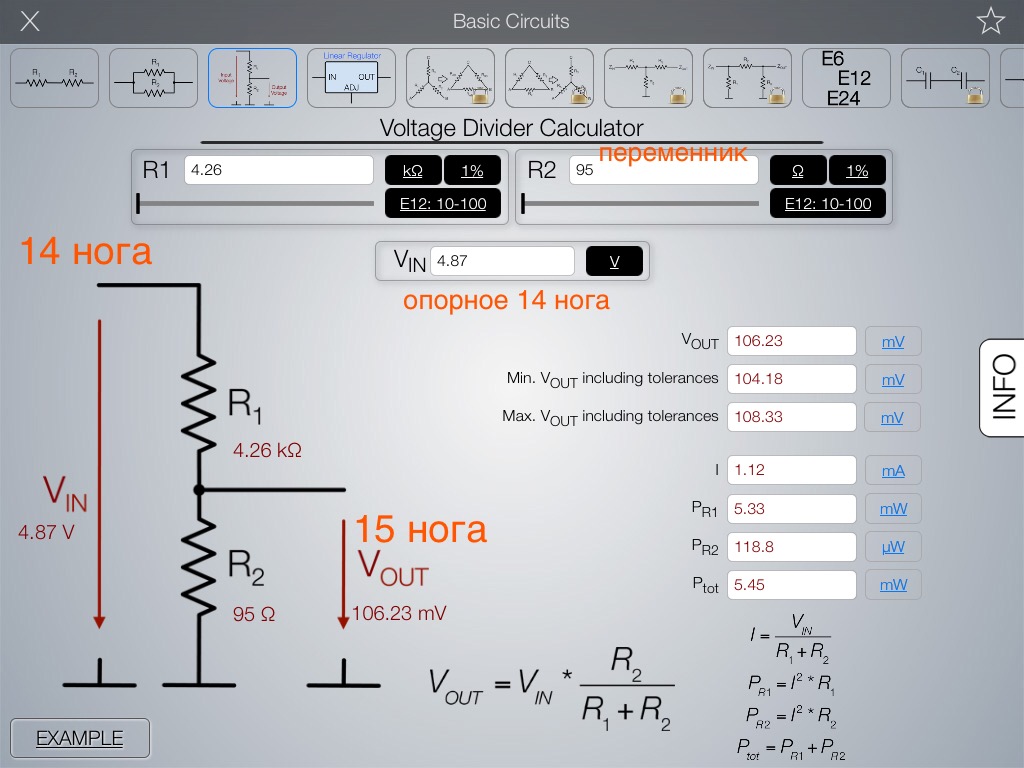
 Эта формула является основной формулой закона Ома.
Эта формула является основной формулой закона Ома.